难度说明：🟢简单🟡中等🔴困难

hot150-17-位运算

🟢01-二进制求和（67）

1.题目内容

给你两个二进制字符串 a 和 b ，以二进制字符串的形式返回它们的和。

示例 1：

输入:a = "11", b = "1"
输出："100"

示例 2：

输入：a = "1010", b = "1011"
输出："10101"

2.题解思路

👻方法1：按位相加（仿链表的两数相加思路）

• 思路分析

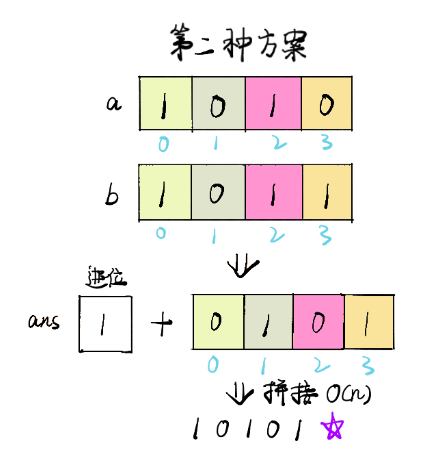
  • 本题思路有点类似于链表的两数相加，通过逆序遍历元素，然后按位相加，记录每个轮次的进位情况，每一轮相加都将当前位值拼入结果（注意此处是逆序比较按位相加，因此最终结果也是要逆序打印）

    

public class Solution1 {
    /**
     * 二进制求和
     */
    public String addBinary(String a, String b) {
        int aLen = a.length(), bLen = b.length();

        StringBuffer sb = new StringBuffer();

        int carry = 0;
        int aPoint = aLen - 1, bPoint = bLen - 1;
        while (aPoint >= 0 || bPoint >= 0) {
            int curA = aPoint >= 0 ? a.charAt(aPoint) - '0' : 0; // 注意字符转数字的处理
            int curB = bPoint >= 0 ? b.charAt(bPoint) - '0' : 0;
            int count = curA + curB + carry;
            sb.append(count > 1 ? count - 2 : count); // 如果count超出1则当前位置要进位，且设定进位

            // 更新carry
            carry = count > 1 ? 1 : 0;

            // 遍历完成，指针移动
            aPoint--;
            bPoint--;
        }

        // 将最后的进位也加上
        if (carry > 0) {
            sb.append(carry);
        }

        // 返回逆序
        return sb.reverse().toString();
    }
}

• 复杂度分析

  • 时间复杂度：

  • 空间复杂度：

👻方法2：硬核法（二进制转十进制相加，然后再将结果转为二进制）

• 思路分析：用工具类将二进制转十进制相加，然后再将结果转为二进制

class Solution {
    public String addBinary(String a, String b) {
        return Integer.toBinaryString(
            Integer.parseInt(a, 2) + Integer.parseInt(b, 2)
        );
    }
}

• 复杂度分析

  • 时间复杂度：

  • 空间复杂度：

🟢02-颠倒二进制位（190）

1.题目内容

颠倒给定的 32 位无符号整数的二进制位。

提示：

• 请注意，在某些语言（如 Java）中，没有无符号整数类型。在这种情况下，输入和输出都将被指定为有符号整数类型，并且不应影响您的实现，因为无论整数是有符号的还是无符号的，其内部的二进制表示形式都是相同的。
• 在 Java 中，编译器使用二进制补码记法来表示有符号整数。因此，在 示例 2 中，输入表示有符号整数 -3，输出表示有符号整数 -1073741825。

示例 1：

输入：n = 00000010100101000001111010011100
输出：964176192 (00111001011110000010100101000000)
解释：输入的二进制串 00000010100101000001111010011100 表示无符号整数 43261596，
     因此返回 964176192，其二进制表示形式为 00111001011110000010100101000000。

示例 2：

输入：n = 11111111111111111111111111111101
输出：3221225471 (10111111111111111111111111111111)
解释：输入的二进制串 11111111111111111111111111111101 表示无符号整数 4294967293，
     因此返回 3221225471 其二进制表示形式为 10111111111111111111111111111111 。

提示：

• 输入是一个长度为 32 的二进制字符串

进阶: 如果多次调用这个函数，你将如何优化你的算法？

2.题解思路

概念补充

左移运算符 <<，可以将一个对象的二进制向左移n位，左边n位丢弃，右边n位补0。比如，a = 1101

• a << 2 = 0100（左移：丢左边 补右边）

右移运算符 >>，可以将一个对象的二进制向右移n位，右边n位丢弃，左边n位补0。比如，a = 1101

• a >> 2 = 0011（右移：丢右边 补左边）

👻方法1：逐位颠倒

• 思路分析
  • 先设置一个结果res的初始值为0；
  • 循环已知的32位二进制数n，先将res左移一位用于存放n的最后一位；
  • res加上n的后一位一直循环，n的低位数就会到res的高位（res的数就是n的反转数），然后将n右移一位去掉最后一位

public class Solution {
    // you need treat n as an unsigned value
    public int reverseBits(int n) {
        int res = 0;
        for(int i = 0; i < 32; i++){
            res <<= 1;
            res |= (n & 1);
            n >>= 1;
        }
        return res;
    }
}

• 复杂度分析

  • 时间复杂度：

  • 空间复杂度：

🟢03-位1的个数（191）

1.题目内容

给定一个正整数 n，编写一个函数，获取一个正整数的二进制形式并返回其二进制表达式中 设置位 的个数（也被称为汉明重量）。

示例 1：

输入：n = 11
输出：3
解释：输入的二进制串 1011 中，共有 3 个设置位。

示例 2：

输入：n = 128
输出：1
解释：输入的二进制串 10000000 中，共有 1 个设置位。

示例 3：

输入：n = 2147483645
输出：30
解释：输入的二进制串 1111111111111111111111111111101 中，共有 30 个设置位

2.题解思路

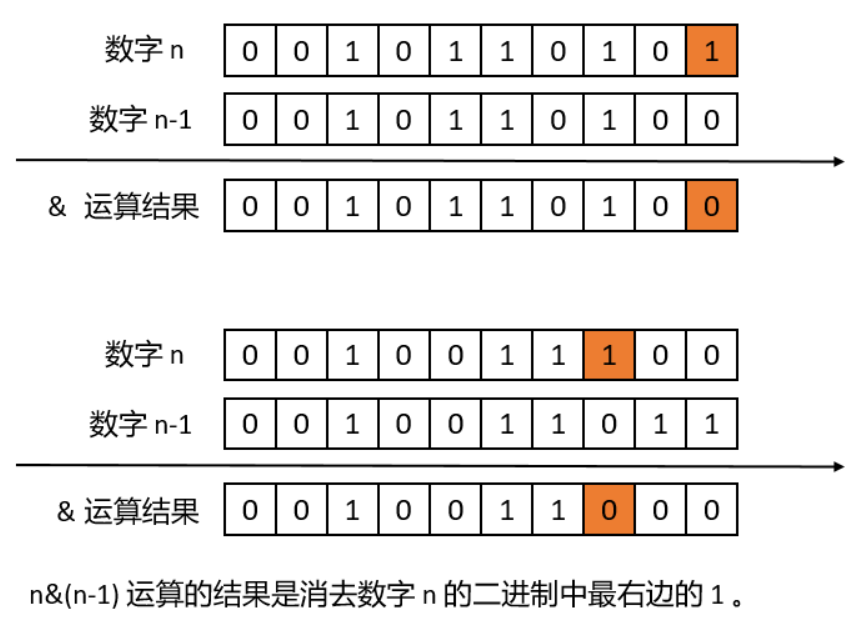
n&(n-1)表示消除数字n的二进制最右边的1，通过这种方式可以借助循环把二进制中的1消除

👻方法1：位运算

​ 二进制中1的个数：位运算

• 思路分析：参考上述思路，当n不为0的时候（n==0就表示没有1了，因此可跳出循环，如果n>0则继续消除1），通过n&(n-1)消除最右边的1

public int bitCount(int n) {
    int count = 0;
    // 每次消去数字n最右边的1，直到全部消掉为止
    while (n != 0) {
        n &= n - 1;
        count++;
    }
    return count;
}

• 复杂度分析

  • 时间复杂度：

  • 空间复杂度：

👻方法2：转化+统计

• 思路分析：
  • 将整数n转化为二进制数据
  • 判断这个二进制字符串中1的个数

/**
 * 191 位1的个数
 */
public class Solution2 {
    public int hammingWeight(int n) {
        // 将十进制转化为二进制数(自定义实现)
        // String nbin = Integer.toBinaryString(n); 借助工具类实现
        StringBuffer nbin = new StringBuffer();
        while (n > 0) {
            nbin.append(n % 2);
            n = n / 2;
        }

        // 判断设置位个数
        int count = 0;
        int x = nbin.length() - 1;
        while (x >= 0) {
            if (nbin.charAt(x) == '1') {
                count++;
            }
            x--;
        }
        // 返回统计结果
        return count;
    }
}

• 复杂度分析

  • 时间复杂度：

  • 空间复杂度：

👻方法3：原生工具类

• 复杂度分析

  • 时间复杂度：

  • 空间复杂度：

public class Solution3 {

    // 位运算
    public int hammingWeight(int n) {
        return Integer.bitCount(n);
    }

}

🟢04-只出现1次的数字（136）

1.题目内容

给你一个 非空 整数数组 nums ，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。

你必须设计并实现线性时间复杂度的算法来解决此问题，且该算法只使用常量额外空间。

2.题解思路

• 思路分析
  • 【思路1】：计数法
  • 【思路2】：哈希表（出现1次入队，出现第2次出队）：如果某个元素出现两次则会被移出，最终哈希表剩下的就是这个出现1次的元素
  • 【思路3】计算和：因为题目具有特殊性，可以从数学角度进行切入，每个重复元素出现两次、某个不重复元素只出现一次，因此可以用集合中元素之和*2-数组之和=不重复元素，即先获取到所有元素，通过这个公式实现计算
  • 【思路4】：异或操作（0的特殊性）

👻方法1：哈希表（重复判断）

public class Solution1 {
    public int singleNumber(int[] nums) {
        Set<Integer> set = new HashSet();
        for(int i = 0;i<nums.length;i++){
            int cur = nums[i];
            if(set.contains(cur)){
                set.remove(cur);
            }else{
                set.add(cur);
            }
        }
        return set.iterator().next();
    }
}

• 复杂度分析

  • 时间复杂度：O（n）

  • 空间复杂度：O（1）

👻方法2：异或（0的特殊性）

此处运用到位运算的技巧，采用异或运算进行一次遍历解决

• 【1】任何数和0做异或运算还是原来的数：a⊕0=a
• 【2】任何数和其自身做异或运算，结果是 0：a⊕a=0
• 【3】异或运算满足交换律和结合律，即 a⊕b⊕a=b⊕a⊕a=b⊕(a⊕a)=b⊕0=b

​ 基于此，因为重复元素都是两个、不重复元素只有一个，因此可以用0去与数组中的每一个元素做异或操作，进而得到这个不重复元素

• 重复元素都是两个：通过【3】，其得到的结果必然是0
• 不重复元素只有一个：通过【1】，0和这个不重复元素做异或操作得到的必然是原数

/**
 * 136 只出现1次的数字
 */
public class Solution2 {
    public int singleNumber(int[] nums) {
        /**
         * 异或思路：
         * 1. 0 和 任何数异或都等于它本身
         * 2. 任何数 和 其本身异或等于0
         * 3.满足交换律
         */
        int res = 0;
        for(int num : nums){
            res ^= num;
        }
        return res;
    }
}

• 复杂度分析

  • 时间复杂度：O（n）

  • 空间复杂度：O（1）

🟡05-只出现1次的数字（137）

1.题目内容

给你一个整数数组 nums ，除某个元素仅出现 一次 外，其余每个元素都恰出现 **三次 。**请你找出并返回那个只出现了一次的元素。

你必须设计并实现线性时间复杂度的算法且使用常数级空间来解决此问题。

示例 1：

输入：nums = [2,2,3,2]
输出：3

示例 2：

输入：nums = [0,1,0,1,0,1,99]
输出：99

2.题解思路

• 思路
  • 【思路1】计数法（通用）
  • 【思路2】计算和：因为题目具有特殊性，可以从数学角度进行切入，每个重复元素出现两次、某个不重复元素只出现一次，因此可以用集合中元素之和*3-数组之和=不重复元素*2，即先获取到所有元素，通过这个公式实现计算
  • 【思路3】

👻方法1：计算和（❌数值溢出）

/**
 * 137 只出现一次的数字II
 */
public class Solution1 {
    public int singleNumber(int[] nums) {
        Set<Integer> set = new HashSet<>();
        int numSum = 0;
        for (int num : nums) {
            numSum += num;
            set.add(num);
        }

        int setSum = 0;
        Iterator<Integer> iterator = set.iterator();
        while (iterator.hasNext()) {
            setSum += iterator.next();
        }

        return (setSum * 3 - numSum) / 2;
    }
}

• 复杂度分析

  • 时间复杂度：

  • 空间复杂度：

🟡06-数字范围按位与（201）

1.题目内容

给你两个整数 left 和 right ，表示区间 [left, right] ，返回此区间内所有数字 按位与 的结果（包含 left 、right 端点）。

示例 1：

输入：left = 5, right = 7
输出：4

示例 2：

输入：left = 0, right = 0
输出：0

示例 3：

输入：left = 1, right = 2147483647
输出：0

2.题解思路

👻方法1：Brian Kernighan 算法

• 思路分析：n & (n-1) 表示移出字符串最右边的1，这个叫做「Brian Kernighan 算法」，它用于清除二进制串中最右边的 1

​ Brian Kernighan 算法的关键在于每次对 number 和 number−1 之间进行按位与运算后，number 中最右边的 1 会被抹去变成 0

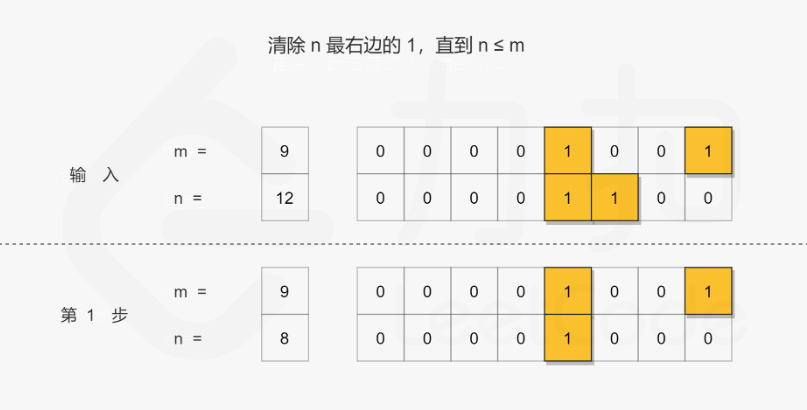
​ 基于上述技巧，可以用它来计算两个二进制字符串的公共前缀。其思想是，对于给定的范围 [m,n]（m<n），可以对数字 n 迭代地应用上述技巧，清除最右边的 1，直到它小于或等于 m，此时非公共前缀部分的 1 均被消去。因此最后返回 n 即可

/**
 * 数字范围按位与（201）
 */
public class Solution1 {

    public int rangeBitwiseAnd(int left, int right) {
        while(left<right){
            right = right & (right-1);
        }
        return right;
    }

}

• 复杂度分析

  • 时间复杂度：

  • 空间复杂度：