hot150-15-二分查找

holic-x...大约 24 分钟

难度说明：🟢简单🟡中等🔴困难

hot150-15-二分查找

二分查找通用规律

    /**
     * 范围查询规律
     * 初始化:
     *   int left = 0;
     *   int right = nums.length - 1;
     * 循环条件
     *   left <= right
     * 右边取值
     *   right = mid - 1
     * 左边取值
     *   left = mid + 1
     * 查询条件
     *   >= target值, 则 nums[mid] >= target时, 都减right = mid - 1
     *   >  target值, 则 nums[mid] >  target时, 都减right = mid - 1
     *   <= target值, 则 nums[mid] <= target时, 都加left = mid + 1
     *   <  target值, 则 nums[mid] <  target时, 都加left = mid + 1
     * 结果
     *   求大于(含等于), 返回left
     *   求小于(含等于), 返回right
     * 核心思想: 要找某个值, 则查找时遇到该值时, 当前指针(例如right指针)要错过它, 让另外一个指针(left指针)跨过他(体现在left <= right中的=号), 则找到了
     */

🚀二分查找区间技巧

注意点

（1）数据溢出问题

中点取值int mid = (left + right)/2存在数据溢出问题，因此调整为int mid = left + (right - left)/2（先减后加，避免相加后数据太大导致数据溢出问题）

（2）循环退出条件

当查找区间为空的时候循环结束

（3）区间取值问题（不同区间取值的处理）

二分法需注意，区间的定义在于区间内的数（下标）都是还没确定与target的大小关系的，区间外的数是确定了与target的大小关系

初始区间取值
循环退出条件
区间选择

（1）闭区间（`[left,right]`）

// 闭区间
public int binarySearch1(int[] nums, int target) {
    // 定义检索区间
    int left = 0, right = nums.length - 1; // 闭区间
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (target < nums[mid]) {
            // 如果目标在左侧，则右侧缩边
            right = mid - 1;
        } else if (target > nums[mid]) {
            // 如果目标在右侧，则左侧缩边
            left = mid + 1;
        } else {
            return mid;
        }
    }
    // 返回元素可插入的下个位置（如果不存在可以直接返回-1）
    return left; // return -1;
}

public int binarySearch1(int[] nums, int target) {
    // 定义检索区间
    int left = 0, right = nums.length - 1; // 闭区间
    while (left <= right) { // 区间不为空时
        int mid = left + (right - left) / 2;
        if (nums[mid]<target) {
            left = mid + 1; // 取[mid+1,right]区间
        } else{
            right = mid -1; // 取[left,mid-1]区间 （target==nums[mid]的情况也包括在内）
        }
    }
    // 返回元素可插入的下个位置（如果不存在可以直接返回-1）
    return left; // return -1;
}

（2）左闭右开（`[left,right)`）

// 左闭右开区间
public int binarySearch2(int[] nums, int target) {
    // 定义检索区间
    int left = 0, right = nums.length; // 闭区间
    while (left < right) { // 区间不为空时
        int mid = left + (right - left) / 2;
        if (nums[mid]<target) {
            left = mid + 1; // 取[mid+1,right)区间
        } else{
            right = mid ; // 取[left,mid)区间 （target==nums[mid]的情况也包括在内）
        }
    }
    // 返回查找到的target所在索引
    return left; // return right;
}

（3）开区间（`(left,right)`）

// 左闭右开区间
public int binarySearch3(int[] nums, int target) {
    // 定义检索区间
    int left = -1, right = nums.length; // 开区间（左开右开）
    while (left + 1 < right) { // 区间不为空时
        int mid = left + (right - left) / 2;
        if (nums[mid] < target) {
            left = mid; // 取(mid,right)区间
        } else {
            right = mid; // 取(left,mid)区间 （target==nums[mid]的情况也包括在内）
        }
    }
    // 返回查找到的target所在索引
    return right;
}

🟢01-搜索插入位置（35）

1.题目内容

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

请必须使用时间复杂度为 O(log n) 的算法。

2.题解思路

👻方法1：二分查找（O(logN)）🚀（二分查找思路）

public class Solution2 {
    public int searchInsert(int[] nums, int target) {
        int len = nums.length;
        int start = 0, end = len - 1;
        while (start <= end) {
            // 获取中间点
            int mid = (start + end) / 2; // 注意梳理数据溢出问题，先减后加：int mid = left + (right-left)/2
            // 判断target所在区间
            if (target < nums[mid]) {
                // target 在左区间，右指针缩边
                end = mid - 1;
            } else if (target == nums[mid]) {
                return mid;
            } else if (target > nums[mid]) {
                // target 在右区间，左指针缩边
                start = mid + 1;
            }
        }
        return start;
    }
}

复杂度分析
- 时间复杂度：O(logN)
空间复杂度：O(1) 常数级别的检索

另一种写法

public int searchInsert(int[] nums, int target) {
    int len = nums.length;
    int left = 0, right = len - 1;
    while (left <= right) {
        int mid = left + (right - left) / 2; // 中间节点的索引位置
        // 判断target在哪个区间
        if (target <= nums[mid]) {
            // target在左区间，right缩边
            right = mid - 1;
        } else {
            // target在右区间，left缩边
            left = mid + 1;
        }
    }
    return left;
}

在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了旋转，使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。

给你 旋转后 的数组 nums 和一个整数 target ，如果 nums 中存在这个目标值 target ，则返回它的下标，否则返回 -1 。

你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

示例 1：

输入：nums = [4,5,6,7,0,1,2], target = 0
输出：4

示例 2：

输入：nums = [4,5,6,7,0,1,2], target = 3
输出：-1

示例 3：

输入：nums = [1], target = 0
输出：-1

2.题解思路

思路分析

【思路1】中规中矩，二分法的思路是对有序数组进行操作，题目中数组原本有序，但是由于旋转规则未知，因此无法直接用二分法，最硬核的就是先排序，后二分，或者直接遍历检索，但是这种方式显然不满足要求

【思路2】基于思路1中引申的问题进一步思考，可以看到经过旋转后的数组是局部有序的，通过这个轴点将数组划分为升序的两部分。因此可以将这个题目转化为寻找这个轴点，如果轴点存在则说明出现了旋转（根据轴点拆分为两个数组，然后分别进行二分），如果没有出现轴点则说明数组没有旋转，则直接可以对整个数组进行二分

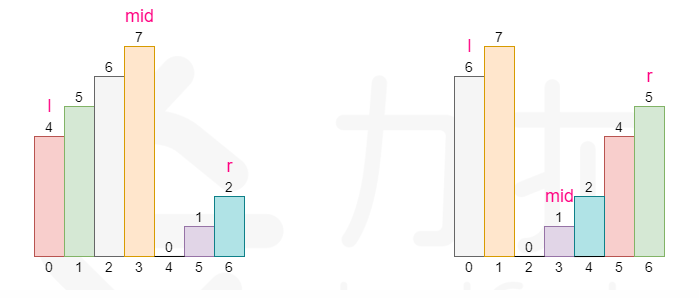
👻方法1：找轴点+分段二分

思路分析
- 找轴点：
  - 数组本身有序，如果经过旋转后则必然会存在突然断序的情况（即连续升序，断开的那个点就是轴点）
  - 数组为空、数组长度为0或者1都视作无旋转
- 分段二分：
  - 如果轴点不存在，则说明数组没有旋转，直接对整个数组进行二分查找
  - 如果轴点存在，则说明数组通过轴点旋转，则对数组进行切割然后分别二分获取结果

/**
 * 33 搜索旋转数组
 */
public class Solution1 {

    /**
     * 思路：找轴点+分段二分
     */
    public int search(int[] nums, int target) {

        int findPoint = getPoint(nums);
        if (findPoint == -1) {
            // 不存在轴点（无旋转），可以直接对整个数组进行二分
            return binarySearch(nums, target);
        }

        // 存在轴点的情况处理（分段二分）
        int[] leftNums = Arrays.copyOfRange(nums, 0, findPoint + 1);
        int[] rightNums = Arrays.copyOfRange(nums, findPoint + 1, nums.length);
        int leftSearch = binarySearch(leftNums, target);
        int rightSearch = binarySearch(rightNums, target);
        // 校验结果(数据只有存在与左侧或右侧)
        // 如果左侧结果存在则返回
        if (leftSearch != -1) {
            return leftSearch;
        }
        // 如果左侧结果不存在则返回右侧结果
        if (rightSearch != -1) {
            return rightSearch + leftNums.length;
        }
        return -1;
    }


    /**
     * 寻找轴点：判断数组是否旋转
     * 如果未旋转（完全升序）：返回-1（表示轴点不存在）
     * 如果存在旋转（存在降序）：返回轴点索引位置
     */
    public int getPoint(int[] nums) {
        // 判断数组边界
        if (nums == null || nums.length == 0 || nums.length == 1) {
            return -1;
        }
        // 判断是否完全升序
        for (int i = 0; i < nums.length - 1; i++) { // 注意数组边界处理
            if (nums[i] > nums[i + 1]) {
                // 出现降序，则轴点位置存在
                return i;
            }
        }
        return -1;
    }

    // 二分法检索
    public int binarySearch(int[] nums, int target) {
        int left = 0, right = nums.length - 1;
        while (left <= right) {
            int mid = left + (right - left) / 2;
            // 判断target是否匹配
            if (nums[mid] == target) {
                return mid;
            } else if (nums[mid] < target) {
                left = mid + 1;
            } else if (nums[mid] > target) {
                right = mid - 1;
            }
        }
        // 结果不存在
        return -1; // return left 表示下一个可插入的位置
    }

}

复杂度分析
- 时间复杂度：O（logN）
- 空间复杂度：O（n）如果数组被旋转，则需要借助辅助的数组来分段二分

算法优化：基于原数组进行检索（不使用copyOfRange）

当确认了旋转基点之后，此处不需要单独copy数组进行切分，而是在原数组基础上直接限定范围进行二分检索（确定检索的起止点）即可

/**
 * 🟡 033 搜索旋转排序数组 - https://leetcode.cn/problems/search-in-rotated-sorted-array/description/
 */
public class Solution033_01 {

    /**
     * 思路：寻转旋转基点 + 二分检索，区分有旋转和无旋转两种情况分析
     */
    public int search(int[] nums, int target) {
        int findRotateIdx = searchRotateIdx(nums);
        if (findRotateIdx == -1) {
            // 无旋转，直接调用二分法检索
            return binarySearch(nums, 0, nums.length - 1, target);
        } else {
            // 有旋转，拆分数组进行二分法检索
            int find1 = binarySearch(nums, 0, findRotateIdx - 1, target);
            int find2 = binarySearch(nums, findRotateIdx, nums.length - 1, target);
            return find1 != -1 ? find1 : find2;
        }
    }

    // 寻找旋转基点
    private int searchRotateIdx(int[] nums) {
        int idx = -1;
        for (int i = 1; i < nums.length; i++) {
            if (nums[i] <= nums[i - 1]) {
                idx = i;
                break; // 出现骤降点
            }
        }
        return idx;
    }

    /**
     * 二分检索(针对指定检索范围)
     */
    private int binarySearch(int[] nums, int start, int end, int target) {
        int left = start, right = end;
        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] == target) {
                return mid;
            } else if (target < nums[mid]) {
                right = mid - 1;
            } else if (target > nums[mid]) {
                left = mid + 1;
            }
        }
        return -1; // 未找到指定target
    }

}

🟡05-在排序数组中查找元素的第1个和最后1个位置（34）🚀

1.题目内容

给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。

示例 1：

输入：nums = [5,7,7,8,8,10], target = 8
输出：[3,4]

示例 2：

输入：nums = [5,7,7,8,8,10], target = 6
输出：[-1,-1]

示例 3：

输入：nums = [], target = 0
输出：[-1,-1]

2.题解思路

👻方法1：low_bound 概念🚀

思路分析

核心思路：掌握二分查找的三种方式的任意一种，然后将二分查找进行分类>=、>、<=、<，转化成>x的进行求解

设定任意一种二分查找的方式（闭区间、左闭右开区间、开区间），将有序整数数组上的二分查找分为4种类型，分别是>=、>、<=、<，而这四种类型是可以相互转化的

例如查找>x的位置，实际上可以等价于查找>= x+1 的位置
类似地如果是<x的位置，则可以等价于查找(>=x) -1即大于等于x的的那个数的左边的数
类似地如果是<=x的位置，则可以等价于查找(>x) -1即大于等于x的的那个数的左边的数

思路分析：题目中要求的是目标值在数组中的开始位置和结束位置即>=x和<=x的位置

// 闭区间
public int low_bound (int[] nums, int target) {
    // 定义检索区间
    int left = 0, right = nums.length - 1; // 闭区间
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (target < nums[mid]) {
            // 如果目标在左侧，则右侧缩边
            right = mid - 1;
        } else if (target > nums[mid]) {
            // 如果目标在右侧，则左侧缩边
            left = mid + 1;
        } else {
            return mid;
        }
    }
    // 返回元素可插入的下个位置（如果不存在可以直接返回-1）
    return left; // return -1;
}

/**
     * 检索法: 二分检索
     * 转化为查找>=x的位置和<=x（（ > x） - 1）的位置
     */

public int[] searchRange(int[] nums, int target) {
    int startIdx = -1,endIdx = -1;
    // 先检索第1个满足的target索引
    startIdx = lowBound(nums,target);
    if (startIdx == nums.length || nums[startIdx]!=target){
        // 元素不存在
        return new int[]{-1,-1};
    }
    // 如果firstIdx存在，则继续寻找endIdx的值
    endIdx = lowBound(nums,target + 1) - 1; // 寻找到>x的位置，定位到其前一个数
    return new int[]{startIdx,endIdx};
}


public int lowBound(int[] nums, int target) {
    // 定义检索区间
    int left = 0, right = nums.length - 1; // 闭区间
    while (left <= right) { // 区间不为空时
        int mid = left + (right - left) / 2;
        if (nums[mid] < target) {
            left = mid + 1; // 取[mid,+1,right]区间
        } else {
            right = mid - 1; // 取[left,mid-1]区间 （target==nums[mid]的情况也包括在内）
        }
    }
    // 返回元素可插入的下个位置（如果不存在可以直接返回-1）
    return left; // return -1;
}

复杂度分析
- 时间复杂度：O（log n）
- 空间复杂度：O（1）常数级别的应用

👻方法2：暴力法

核心：循环遍历数组（数组本身升序排列），定义一个数组存储结果集合，这个结果集可以理解为（第一个匹配的元素索引，第一个匹配的元素索引+匹配个数（作为结束索引））

// 暴力法：循环遍历数组，一次进行校验
public int[] searchRange(int[] nums, int target) {
    // 定义结果集(开始索引,结束索引)
    int[] res = {-1,-1};
    // 定义target在数组中的匹配个数(计数器)
    int count = 0;
    for (int i = 0; i < nums.length; i++) {
        if (nums[i] == target) {
            if(count == 0){
                // 表示第一个检索到的匹配元素，将其加入结果集
                res[0] = i;
            }
            count++;
        }
    }
    // 最终封装结果集并返回
    if(res[0] != -1){
        res[1] = res[0] + count -1;
    }
    return res;
}

👻方法3：正向二分+逆向二分

思路分析：正向二分找左边界 + 逆向二分找右边界

复杂度分析
- 时间复杂度：
- 空间复杂度：

🟡06-寻找旋转排序数组中的最小值（153）

1.题目内容

已知一个长度为 n 的数组，预先按照升序排列，经由 1 到 n 次旋转后，得到输入数组。例如，原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到：

若旋转 4 次，则可以得到 [4,5,6,7,0,1,2]
若旋转 7 次，则可以得到 [0,1,2,4,5,6,7]

注意，数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。

给你一个元素值 互不相同 的数组 nums ，它原来是一个升序排列的数组，并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。

你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

2.题解思路

👻方法1：二分法

思路分析：旋转后的数组一定会被划分为前后两部分的升序数组，且前面部分的最小值一定大于后一半的最大值，因此只要通过二分法找到后半部分的第1个元素即可。采用二分查找思路，然后不断缩小区间取值

/**
 * 153 寻找旋转排序数组的中的最小值
 */
public class Solution1 {

    /**
     * 遍历法
     */
    public int findMin(int[] nums) {
        // 初始化最小值
        int min = nums[0];

        // 闭区间思路
        int left = 0, right = nums.length - 1;
        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] < min) {
                // 如果mid所在位置元素小于min，则其左侧可能还会存在比min更小的数，因此要更新min的值，右侧缩边
                min = nums[mid];
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        }

        // 返回最小值
        return min;
    }

}

复杂度分析
- 时间复杂度：O（log n）二分检索
- 空间复杂度：O（1）常数级别的空间占用

👻方法2：规律法

思路分析：结合题意分析，未知数组是否旋转，如果数组出现旋转则这个排序数组必然会出现突然断序的情况，则这个断续的位置就是最小值所在位置，因此可以通过遍历继续数组元素进行判断。如果数组元素连续升序则说明无旋转（最小值就是第1个），如果数组元素遍历过程中出现断序的情况，则断续位置就是最小值

public class Solution1 {
    /**
     * 遍历法
     */
    public int findMin(int[] nums) {
        int idx = validRotate(nums);
        return idx == -1 ? nums[0] : nums[idx];
    }

    public int validRotate(int[] nums) {
        int idx = -1; // 如果无旋转则返回-1
        // 如果数组为空或者数组长度为1则视作没有旋转
        if (nums == null || nums.length == 0 || nums.length == 1) {
            return -1;
        }
        // 判断数组是否连续升序
        for (int i = 0; i < nums.length - 1; i++) {
            if (nums[i] > nums[i + 1]) { // 连续升序出现断序
                idx = i + 1; // 此处取i+1表示这个位置是最小的数
            }
        }
        return idx;
    }
}

复杂度分析
- 时间复杂度：O（n）最差的情况需要遍历整个数组，n为数组长度
- 空间复杂度：O（1）只需要常数级的空间占用

🔴07-寻找两个正序数组的中位数（04）

1.题目内容

给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。

算法的时间复杂度应该为 O(log (m+n)) 。

示例 1：

输入：nums1 = [1,3], nums2 = [2]
输出：2.00000
解释：合并数组 = [1,2,3] ，中位数 2

示例 2：

输入：nums1 = [1,2], nums2 = [3,4]
输出：2.50000
解释：合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5

2.题解思路

👻方法1：合并排序数组 + 奇偶找中位（❌非O（logn））

/**
 * 004 寻找两个正序数组的中位数
 */
public class Solution1 {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int[] mergeNums = merge(nums1, nums2);

        int len = mergeNums.length;
        if (len % 2 == 0) {
            // 偶数
            int left = 0, right = len - 1;
            int mid = left + (right - left) / 2;
            return ((double) mergeNums[mid] + (double)mergeNums[mid+1]) / 2; // 需将int转为double做除法
        } else {
            // 奇数
            return mergeNums[mergeNums.length / 2];
        }
    }

    // 合并两个有序数组
    public int[] merge(int[] nums1, int[] nums2) {
        int len1 = nums1.length, len2 = nums2.length;
        // 定义数组存储合并后的内容
        int[] nums = new int[len1 + len2];
        // 定义数组指针，分别装箱nums、nums1、nums2当前遍历位置
        int cur = 0, p1 = 0, p2 = 0;
        while (p1 < len1 && p2 < len2) {
            // 如果p1指向元素较小则加入nums1[p1]
            if (nums1[p1] < nums2[p2]) {
                nums[cur] = nums1[p1];
                // 指针后移
                cur++;
                p1++;
            } else {
                nums[cur] = nums2[p2];
                // 指针后移
                cur++;
                p2++;
            }
        }

        // 判断是否有多余长度的元素需补充
        while (p1 < len1) {
            nums[cur] = nums1[p1];
            cur++;
            p1++;
        }
        while (p2 < len2) {
            nums[cur] = nums2[p2];
            cur++;
            p2++;
        }

        // 返回合并后的有序数组
        return nums;
    }
}

复杂度分析
- 时间复杂度：O（m+n）遍历所有元素进行合并
空间复杂度：O（m+n）需m+n空间存储合并后的排序数组

昵称

邮箱

网址

按正序
按倒序
按热度

hot150-15-二分查找

预览: