难度说明：🟢简单🟡中等🔴困难

hot100-14-贪心算法

学习资料

• 代码随想录-贪心算法

贪心算法一般分为如下四步：

• 将问题分解为若干个子问题
• 找出适合的贪心策略
• 求解每一个子问题的最优解
• 将局部最优解堆叠成全局最优解

​ 但是这些步骤说明显然过于理论化，反而难以切入。而实际上贪心算法的场景很难完全按照这四个步骤去思考（因为要去验证贪心算法的正确性、排除异常的一些情况），如果单纯按照这几个步骤思考反而会陷进去。因此在一些场景中往往会通过常识性推导+举反例来验证贪心策略的正确性，在切入场景的过程中只需要思考局部最优是什么，从局部最优推导出全局最优，这个思考的步骤也往往是比较抽象的，没有具体的解题套路和模板。

🟢01-买卖股票的最佳时机（一锤定音）（121）

1.题目内容

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格

你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。

返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0

问题核心：操作一次股票买卖

2.题解思路

❌方法1：暴力法（超时）

​ 直接循环遍历依次找到任意两个数的查找，然后定义一个max存储这个遍历过程中产生的差值的最大结果

// 思路1：暴力法
public int maxProfit(int[] prices) {
    // 依次遍历判断任意两个元素之间的差值，记录最大利润值
    int maxProfit = 0;
    for(int i = 0; i < prices.length; i++) {
        for(int j = i+1; j < prices.length; j++) { // 卖出时间要晚于买入时间
            if(prices[j] > prices[i]) { // 至少要获取利润
                maxProfit = Math.max(maxProfit, prices[j] - prices[i]);
            }
        }
    }
    // 返回结果
    return maxProfit;
}

• 复杂度分析

  • 时间复杂度：O(n²)，n为数组大小

  • 空间复杂度：O(1)，只需一个变量存储最大值

👻方法2：一次遍历（贪心思路：假设以历史最低价格买入，择日卖出）

​ 核心：记录股票历史价格最低点，然后每天都假设是在历史价格最低点买入，然后执行卖出操作计算可以赚多少钱。一次遍历结束则可以得到最大利润

​ 假设给定的数组是【7，1，5，3，6，4】，则其描绘图示如下

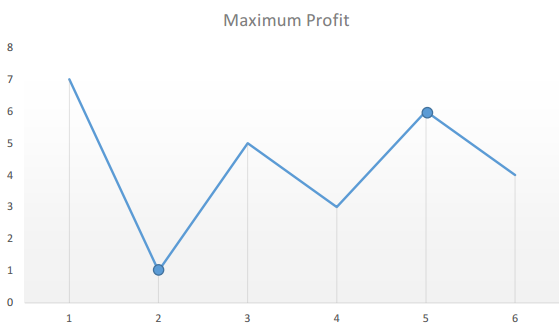
​ 假设自己来购买股票。随着时间的推移，每天都可以选择出售股票与否。那么，假设在第 i 天，如果要在今天卖股票，那么能赚多少钱呢？

​ 显然，如果真的在买卖股票，肯定会想：如果是在历史最低点买的股票就好了！只要用一个变量记录一个历史最低价格 minprice，就可以假设自己的股票是在那天买的。那么在第 i 天卖出股票能得到的利润就是 prices[i] - minprice（因为此处限定了股票不能当天卖出，所以只需要关注历史价格最低点和当日价格的差值即为当前的最大利润，当考虑完所有的天数，最终即可得到最终的最大利润值）。也就是说此处的minprice并不是全局的最低点，而是当天之前的历史最低点，这个历史最低点是可以在一次遍历的过程中附带记录的

​ 因此，只需要遍历价格数组一遍，记录历史最低点，然后在每一天考虑这么一个问题：如果是在历史最低点买进的，那么今天卖出能赚多少钱？当考虑完所有天数之时，就得到了最好的答案

// 思路2：贪心算法
public int maxProfit(int[] prices) {
    // 记录最大利润值
    int maxProfit = 0;
    // 记录股票的历史价格最低点（非全局最低点）
    int hisMinPrice = Integer.MAX_VALUE;
    // 一次遍历的过程中记录hisMinPrice的同时，并假设每天如果是在hisMinPrice位置买入然后执行卖出的利润，考虑所有的天数并同步更新最大利润值
    for(int i = 0; i < prices.length; i++) {
        // 计算假设在hisMinPrice位置买入，今天卖出股票能得到的利润值，并更新maxProfit
        maxProfit = Math.max(maxProfit, prices[i] - hisMinPrice);
        // 更新历史记录最低点
        hisMinPrice = Math.min(hisMinPrice, prices[i]);
    }
    // 返回结果
    return maxProfit;
}

• 复杂度分析

  • 时间复杂度：O(n)

  • 空间复杂度：O(1)

3.扩展题型

👻扩展：买卖股票的最佳时机II

​ 给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格

​ 设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易（多次买卖一支股票）

​ 注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）

示例 1:

• 输入: [7,1,5,3,6,4]
• 输出: 7
• 解释: 在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4。随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6-3 = 3

示例 2:

• 输入: [1,2,3,4,5]
• 输出: 4
• 解释: 在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。注意你不能在第 1 天和第 2 天接连购买股票，之后再将它们卖出。因为这样属于同时参与了多笔交易，你必须在再次购买前出售掉之前的股票

示例 3:

• 输入: [7,6,4,3,1]
• 输出: 0
• 解释: 在这种情况下, 没有交易完成, 所以最大利润为 0

问题核心：可多次操作股票，获取最大利润

一次遍历（贪心思路：利润拆分，收集正利润）

​ 如果基于利润分解的思路，可以将本题结合如下思路理解：

• 假设第0天买入，第3天卖出，则利润为prices[3] - prices[0]，其等价于(prices[3] - prices[2]) + (prices[2] - prices[1]) + (prices[1] - prices[0])
• 也就是说，将利润分解为每天为单位的维度，而不是以一个整体的思路去考虑。也就是说每次都是今天买隔日卖（低买高卖）的思路去做，如果这个操作有利润就落袋为安，如果没有利润则不去做这个操作（相当于没有买卖）
  • 股票价格：【7，1，5，10，3，6，4】
  • 每日利润：【0，-6，4，5，-7，3，-2】（首日是没有利润的，贪心的思路是只收集每天的正利润）

public int maxProfit(int[] prices) {
    // 记录最大利润值
    int maxProfit = 0;
    // 一次遍历的过程，叠加每次低买高卖的正利润操作（从第2天开始可以卖前一天的票,且首日是没有利润的）
    for (int i = 1; i < prices.length; i++) {
        maxProfit += Math.max(prices[i] - prices[i - 1], 0);
    }
    // 返回结果
    return maxProfit;
}

• 复杂度分析

  • 时间复杂度：O(n)，n为数组长度

  • 空间复杂度：O(1)

🟡02-跳跃游戏（55）

1.题目内容

给你一个非负整数数组 nums ，你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。

判断你是否能够到达最后一个下标，如果可以，返回 true ；否则，返回 false 。

示例 1：

输入：nums = [2,3,1,1,4]
输出：true
解释：可以先跳 1 步，从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。

示例 2：

输入：nums = [3,2,1,0,4]
输出：false
解释：无论怎样，总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 ， 所以永远不可能到达最后一个下标

2.题解思路

👻方法1：范围覆盖（推荐）

​ 核心：判断并更新每个节点的范围覆盖的最大值，如果最终cover大于终点坐标则说明是可达的（这道题目关键点在于：不用拘泥于每次究竟跳几步，而是看覆盖范围，覆盖范围内一定是可以跳过来的，不用管是怎么跳的）

class Solution {
    public boolean canJump(int[] nums) {
        if (nums.length == 1) {
            return true;
        }
        //覆盖范围, 初始覆盖范围应该是0，因为下面的迭代是从下标0开始的
        int coverRange = 0;
        //在覆盖范围内更新最大的覆盖范围（此处必须是限定覆盖范围内更新，否则中间节点有可能不可达，i只能在覆盖范围内移动）
        for (int i = 0; i <= coverRange; i++) {
            coverRange = Math.max(coverRange, i + nums[i]);
            // 如果当前覆盖范围大于终点坐标，说明是可达终点的（此处在遍历过程中进行判断，不需要等到最后）
            if (coverRange >= nums.length - 1) {
                return true;
            }
        }
        return false;
    }
}

• 复杂度分析

  • 时间复杂度：O(n)

  • 空间复杂度：O(1)

👻方法2：加油站思维

​ 核心：类似加油站加油场景，判断当前已走里程+加油里程能否支撑汽车走到下一个节点

​ 可以结合实际场景案例分析：假设设定了N个加油站（n对应数组元素个数），每到一个加油站可以进行加油（nums[i]为最大加油油量），要看已走里程+站点的加油里程能否走到下一个节点，如果可以则一直延续到终点即可，如果中间某个环节不行则是无法到达终点的

​ 在这个过程中必须始终选择可覆盖的最大范围，而不是"累加"概念

public boolean canJump(int[] nums) {
    int max = 0; // 此前可支撑的最大里程
    for(int i=0;i<nums.length;i++){
        // 判断当前的最大里程是否可以支持走到当前节点
        if(max<i){
            return false; // 无法走到当前节点
        }
        // 更新最大的覆盖范围（此处并不是简单的max+=nums[i]）
        max = Math.max(max, i + nums[i]);
    }
    return true;
}

• 复杂度分析

  • 时间复杂度：O(n)

  • 空间复杂度：O(1)

👻方法3：倒序遍历

​ 核心：倒着走看能不能跳到

​ 从正向分析来看，可能会陷入究竟应该怎么跳，才能让其可以跳到最后一个下标。实际上这个题目只需要判断是否可以跳到最后一个下标，而不用关心"具体的过程"，因此此处可以简化题意，我并不care前面怎么跳，只关心我'"最后一步是否可以跳到目标位置"'，而这个则取决于其前面一步的下标指定的步数是否满足可以目标下标

​ 从逆向的角度思考，从数组尾部开始遍历，去找一个数（这个数满足其数值大于等于步数，所谓步数就是这个数和目标值的坐标差值），如果存在这个数则变相说明正向可以跳到目标位置，不断地向左边缩圈（即一直往左去找它的上一步满足条件的坐标），直到循环结束

• 复杂度分析

  • 时间复杂度：

  • 空间复杂度：

🟡03-跳跃游戏II（45）

1.题目内容

给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。

每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说，如果你在 nums[i] 处，你可以跳转到任意 nums[i + j] 处:

• 0 <= j <= nums[i]
• i + j < n

返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。

示例 1:

输入: nums = [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
     从下标为 0 跳到下标为 1 的位置，跳 1 步，然后跳 3 步到达数组的最后一个位置。

示例 2:

输入: nums = [2,3,0,1,4]
输出: 2

2.题解思路

👻方法1：反向查找出发位置

​ 目标是到达数组的最后一个位置，因此我们可以考虑最后一步跳跃前所在的位置，该位置通过跳跃能够到达最后一个位置。

​ 如果有多个位置通过跳跃都能够到达最后一个位置，那么我们应该如何进行选择呢？直观上来看，我们可以「贪心」地选择距离最后一个位置最远的那个位置，也就是对应下标最小的那个位置。因此，我们可以从左到右遍历数组，选择第一个满足要求的位置。

​ 找到最后一步跳跃前所在的位置之后，我们继续贪心地寻找倒数第二步跳跃前所在的位置，以此类推，直到找到数组的开始位置

class Solution {
    public int jump(int[] nums) {
        int position = nums.length - 1;
        int steps = 0;
        while (position > 0) {
            for (int i = 0; i < position; i++) {
                if (i + nums[i] >= position) {
                    position = i;
                    steps++;
                    break;
                }
            }
        }
        return steps;
    }
}

• 复杂度分析

  • 时间复杂度：O(n²)

  • 空间复杂度：O(1)

👻方法2：跳槽思维

​ 把该问题比喻为入职，数组下标是公司级别(入职门槛)，对应的值是公司级别之上的级别成长空间。你想用最少的跳槽次数入职最高级的公司

• 数组[2,3,1,2,4,2,3]
• 下标 0 1 2 3 4 5 6

​ 最开始你没有工作，你的水平是2级，可以在2级及以下的公司里随便挑，此时候选公司有下标1和2

​ 注意：如果你想进入更高级别的公司，应该选择能够帮助你提升级别最多的公司。例如，公司1能够将你的级别提升到1+3=4级，而公司2只能提升到2+1=3级。显然，你应该选择公司1，然后升到4级。接下来，你可以跳槽到4级及以下的公司，每次都选择能够帮助你提升最多级别的公司，如此循环……直到水平级别足够入职梦中情司

​ 只有每次跳槽都选择能够帮助你升级最多的公司，才能以最少的跳槽次数到达最高级别的公司

​ PS：此处题目生成的测试用例都是可达的，因此此处钻的点在于，认为每次都能以最小步数达到终点的思路去做

class Solution {
    public int jump(int[] nums) {
        int ans = 0; //跳槽次数
        int curUnlock = 0; //当前你的水平能入职的最高公司级别
        int maxUnlock = 0; //当前可选公司最多能帮你提到几级
        for (int i = 0; i < nums.length - 1; i++) { //从前向后遍历公司，最高级公司(nums.length-1)是目标，入职后不再跳槽，所以不用看，故遍历范围是左闭右开区间[0,nums.length-1)
            maxUnlock = Math.max(maxUnlock, i + nums[i]); //计算该公司最多能帮你提到几级(公司级别i+成长空间nums[i])，与之前的提级最高记录比较，打破记录则更新记录
            if (i == curUnlock) { // 把你当前水平级别能选的公司都看完了，你选择跳槽到记录中给你提级最多的公司，以解锁更高级公司的入职权限
                curUnlock = maxUnlock; // 你跳槽到了该公司，你的水平级别被提升了
                ans++; //这里记录你跳槽了一次
            }
        }
        return ans; //返回跳槽总次数
    }
}

• 参考：跳跃游戏II 题解

class Solution {
    public int jump(int[] nums) {
        int result = 0;
        // 当前覆盖的最远距离下标
        int end = 0;
        // 下一步覆盖的最远距离下标
        int temp = 0;
        for (int i = 0; i <= end && end < nums.length - 1; ++i) {
            temp = Math.max(temp, i + nums[i]);
            // 可达位置的改变次数就是跳跃次数
            if (i == end) {
                end = temp;
                result++;
            }
        }
        return result;
    }
}

• 复杂度分析

  • 时间复杂度：

  • 空间复杂度：

🟡04-划分字母区间（763）todo

1.题目内容

给你一个字符串 s 。我们要把这个字符串划分为尽可能多的片段，同一字母最多出现在一个片段中。

注意，划分结果需要满足：将所有划分结果按顺序连接，得到的字符串仍然是 s 。

返回一个表示每个字符串片段的长度的列表

示例 1：

输入：s = "ababcbacadefegdehijhklij"
输出：[9,7,8]
解释：
划分结果为 "ababcbaca"、"defegde"、"hijhklij" 。
每个字母最多出现在一个片段中。
像 "ababcbacadefegde", "hijhklij" 这样的划分是错误的，因为划分的片段数较少。 

示例 2：

输入：s = "eccbbbbdec"
输出：[10]

2.题解思路

👻方法1：

• 复杂度分析

  • 时间复杂度：

  • 空间复杂度：