hot150-07-栈

holic-x...大约 14 分钟

难度说明：🟢简单🟡中等🔴困难

hot150-07-栈

🟢01-有效的括号（20）

1.题目内容

给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串 s ，判断字符串是否有效。

有效字符串需满足：

左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
每个右括号都有一个对应的相同类型的左括号。

示例 1：

**输入：**s = "()"

**输出：**true

示例 2：

**输入：**s = "()[]{}"

**输出：**true

示例 3：

**输入：**s = "(]"

**输出：**false

示例 4：

**输入：**s = "([])"

**输出：**true

2.题解思路

👻方法1：替换法

思路分析：题中给定的字符串只包括括号，因此可以采用替换的思路
- 根据指定的括号类型，进行成对替换，如果最终返回空字符串，则说明括号有效

// 替换法：括号是成对出现的，如果成对进行替换，到最后只剩下空字符串，则括号有效
public boolean isValid(String s) {
    while(s.contains("()")|| s.contains("{}") || s.contains("[]")){
        // 替换成对的括号
        s = s.replace("()","");
        s = s.replace("{}","");
        s = s.replace("[]","");
    }

    // 如果最终返回空字符串，则说明括号有效
    return s.isEmpty();
}

复杂度分析
- 时间复杂度：
- 空间复杂度：

👻方法2：栈

思路分析：利用栈先进后出思想，遍历字符串序列，如果是左括号则压栈，如果是右括号则校验栈顶元素的左括号与当前是否匹配（匹配则正常弹出），不匹配则直接return false（表示括号是无效的）

public class Solution2 {

    /**
     * 栈思路：利用栈先进后出的特点
     * 1.构建括号映射Map<k,v> k 为右括号，v为左括号
     * 2.左括号入栈，遇到右括号则出栈进行比较
     */
    public boolean isValid(String s) {
        // 构建括号映射
        Map<Character,Character> map = new HashMap<>();
        map.put(')','(');
        map.put('}','{');
        map.put(']','[');

        // 定义栈存储左括号序列
        Stack<Character> stack = new Stack<>();
        // 遍历字符串序列，如果遇到左括号则入栈，右括号则弹出栈顶元素进行比较
        for(int i=0;i<s.length();i++){
            char cur = s.charAt(i);
            if(map.containsValue(cur)){
                // 遇到左括号则入栈
                stack.push(cur);
            }else if(map.containsKey(cur)){
                // 遇到右括号，则弹出栈顶元素进行比较，确认括号是否一一匹配
                if(stack.isEmpty()||stack.peek()!=map.get(cur)){ // 如果栈为空，或者括号不匹配则为无效的括号，直接返回false
                    return false;
                }else{
                    // 弹出元素，继续下一轮比较
                    stack.pop(); // pop 方法移除并返回栈顶元素
                }
            }
        }
        // 校验最终stack中的元素，如果还存在元素则说明不匹配
        return stack.isEmpty();
    }
}

复杂度分析
- 时间复杂度：O（n）遍历字符串元素
- 空间复杂度：O（n）需要栈空间存储字符串元素（n为字符串长度）

🟡02-简化路径（71）

1.题目内容

给你一个字符串 path ，表示指向某一文件或目录的 Unix 风格 绝对路径 （以 '/' 开头），请你将其转化为 更加简洁的规范路径。

在 Unix 风格的文件系统中规则如下：

一个点 '.' 表示当前目录本身。
此外，两个点 '..' 表示将目录切换到上一级（指向父目录）。
任意多个连续的斜杠（即，'//' 或 '///'）都被视为单个斜杠 '/'。
任何其他格式的点（例如，'...' 或 '....'）均被视为有效的文件/目录名称。

返回的 简化路径 必须遵循下述格式：

始终以斜杠 '/' 开头。
两个目录名之间必须只有一个斜杠 '/' 。
最后一个目录名（如果存在）不能以 '/' 结尾。
此外，路径仅包含从根目录到目标文件或目录的路径上的目录（即，不含 '.' 或 '..'）。

返回简化后得到的 规范路径 。

示例 1：

**输入：**path = "/home/"

输出："/home"

解释：

应删除尾随斜杠。

示例 2：

**输入：**path = "/home//foo/"

输出："/home/foo"

解释：

多个连续的斜杠被单个斜杠替换。

示例 3：

**输入：**path = "/home/user/Documents/../Pictures"

输出："/home/user/Pictures"

解释：

两个点 ".." 表示上一级目录（父目录）。

示例 4：

**输入：**path = "/../"

输出："/"

解释：

示例 5：

**输入：**path = "/.../a/../b/c/../d/./"

输出："/.../b/d"

解释：

"..." 在这个问题中是一个合法的目录名。

2.题解思路

👻方法1：分割 + 栈（双端队列）+ 目录拼接

思路分析
- 分析题意，对names进行分割，names中包括的字符串只能有如下：
  - 空字符串（当出现多个连续的/）就会分割出空字符串
  - 一个点.
  - 两个..
  - 只包含英文字母、数字或者_的目录名
- 遍历字符串元素，对于空字符串和.无需进行处理（空字符串没有意义，而.表示目录本身，无需切换目录），对于..或者目录名可以通过栈维护路径中的每个目录名
  - 当遇到..时就将目录切换到上一级（栈不为空，就弹出栈顶元素）
  - 当遇到目录名就直接入栈
- 按照上述规则遍历字符串，随后依次解析栈内元素进行拼接（顺序：从栈底到栈顶）

/**
 * 071 简化路径
 */
public class Solution1 {
    /**
     * 对于path，切割后的names只有四种形式：空字符串、一个点.、两个点..、目录名
     * 对于空字符串和一个点无需做处理，但对于两个点和目录名的存储可以考虑通过栈来实现
     * 遇到两个点：需切换上级目录（栈不为空弹出栈顶元素）
     * 遇到目录名：入栈
     */
    public String simplifyPath(String path) {

        // 对路径进行分割，解析数据
        String[] names = path.split("/");
        // 解析分割后的数据，获取到目录信息（借助栈存储元素）
        Deque<String> stack = new ArrayDeque<>(); // 此处使用双端队列存储
        for(String name: names){
            if("".equals(name) || ".".equals(name)){
                // 如果是空字符串（////这种情况下分割出来的）或者`.`则不做处理
                continue;
            }else if("..".equals(name)){
                // 对于两个点，需切换上级目录（栈不为空弹出栈顶元素）
                if(!stack.isEmpty()){
                    stack.pollLast(); // 弹出栈顶元素
                }
            }else{
                stack.offerLast(name); // 对于目录名则压栈
            }
        }

        // 遍历栈中元素（按照栈底-栈顶的顺序拼接路径）
        StringBuffer sb = new StringBuffer();
        // 栈为空则表示根目录，栈不为空则依次拼接信息
        if(stack.isEmpty()){
            sb.append("/");
        }else{
            while(!stack.isEmpty()){
                sb.append("/" + stack.pollFirst());
            }
        }

        // 返回拼接后的结果
        return sb.toString();
    }

}

复杂度分析
- 时间复杂度：O（n），n为字符串path的长度
- 空间复杂度：O（n），需要O（n）的空间存储names中所有的字符串

🟡03-最小栈（155）

1.题目内容

设计一个支持 push ，pop ，top 操作，并能在常数时间内检索到最小元素的栈。

实现 MinStack 类:

MinStack() 初始化堆栈对象。
void push(int val) 将元素val推入堆栈。
void pop() 删除堆栈顶部的元素。
int top() 获取堆栈顶部的元素。
int getMin() 获取堆栈中的最小元素。

2.题解思路

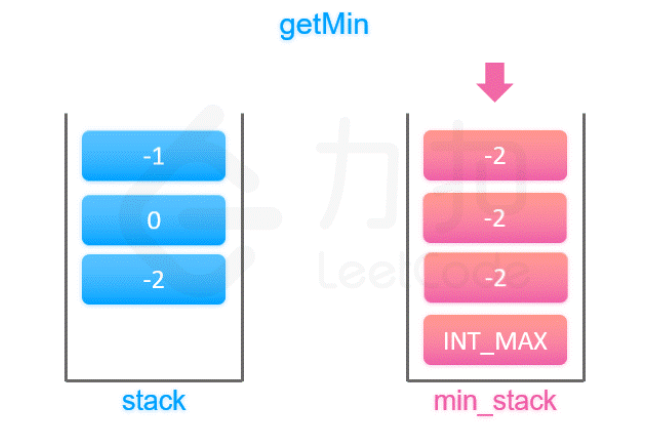
👻方法1：辅助栈（stack + minValStack）

思路分析：通过一个辅助栈，同步记录每个元素入栈后当前栈的最小值，当需要获取到当前栈的最小元素，只需要查看栈顶元素就能跟踪到当前栈状态的最小元素
- 初始化栈：内部定义两个栈，分别用于存储栈元素和对应栈状态下元素的min
  - 对于stack：存储元素
  - 对于minValStack：存储对应状态下的栈的最小值，初始化压入Integer.MAX_VALUE，让其栈顶元素始终指向当前对应状态的栈的最小值
- 入栈：每次入栈的时候同步更新（stack压栈，minValStack则压入当前状态栈的min（将val与栈顶元素比较1次即可））
- 出栈：通过弹出两个栈的栈顶元素
- top：返回stack的栈顶元素
- getMin：返回minValStack的栈顶元素

/**
 * 155 最小栈
 */
public class MinStack {

    // 内部定义两个栈，分别用于存储栈元素和对应栈状态下元素的min
    Stack<Integer> stack ;
    Stack<Integer> minValStack ;

    public MinStack() {
        stack = new Stack<>();
        minValStack = new Stack<>();
        // 初始化时先压入一个min
        minValStack.push(Integer.MAX_VALUE);
    }

    public void push(int val) {
        // 同步入栈,并更新当前的栈的最小值（minValStack栈顶元素始终存储上一状态的栈的最小值，因此每次比较只需要和栈顶元素比较即可）
        int curMin = Math.min(minValStack.peek(),val);
        stack.push(val);
        minValStack.push(curMin);
    }

    public void pop() {
        // 同步出栈，直接弹出栈顶元素
        stack.pop();
        minValStack.pop();
    }

    public int top() {
        // 获取栈顶元素
        return stack.peek();
    }

    public int getMin() {
        // 获取当前栈的最小值(当前minValStack的栈顶元素即指向当前状态的栈的最小值)
        return minValStack.peek();
    }
}

复杂度分析
- 时间复杂度：O（1）所有操作的时间复杂度均为O（1）（栈的插入、删除、读取操作均为O（1））
- 空间复杂度：O（n），n为总操作数，需要辅助栈空间。如果连续插入n个元素则两个栈的占用空间复杂度为O（n）

🟡04-逆波兰表达式求值（150）

1.题目内容

给你一个字符串数组 tokens ，表示一个根据逆波兰表示法open in new window 表示的算术表达式。

请你计算该表达式。返回一个表示表达式值的整数。

注意：

有效的算符为 '+'、'-'、'*' 和 '/' 。
每个操作数（运算对象）都可以是一个整数或者另一个表达式。
两个整数之间的除法总是 向零截断 。
表达式中不含除零运算。
输入是一个根据逆波兰表示法表示的算术表达式。
答案及所有中间计算结果可以用 32 位 整数表示。

示例 1：

输入：tokens = ["2","1","+","3","*"]
输出：9
解释：该算式转化为常见的中缀算术表达式为：((2 + 1) * 3) = 9

示例 2：

输入：tokens = ["4","13","5","/","+"]
输出：6
解释：该算式转化为常见的中缀算术表达式为：(4 + (13 / 5)) = 6

示例 3：

输入：tokens = ["10","6","9","3","+","-11","*","/","*","17","+","5","+"]
输出：22
解释：该算式转化为常见的中缀算术表达式为：
  ((10 * (6 / ((9 + 3) * -11))) + 17) + 5
= ((10 * (6 / (12 * -11))) + 17) + 5
= ((10 * (6 / -132)) + 17) + 5
= ((10 * 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22

2.题解思路

👻方法1：栈

思路分析：借助栈存储操作元素，辅助操作
- 遍历表达式元素
  - 数字处理（压栈）；如果是数字则压栈
  - 符号处理（取2个元素出栈+根据符号计算结果+结果入栈）：如果是符号，则需从栈中取出两个元素进行符号运算（栈：先进后出，因此先出来的是右操作数，后出来的是左操作数），随后将得到的新结果入栈
- 表达式遍历完成，最终栈内只有一个元素，得到的即为结果

/**
 * 150 逆波兰表达式求值
 */
public class Solution1 {

    /**
     * 遍历数组元素，借助栈辅助操作
     * 1.如果是数字则入栈
     * 2.如果是操作符，则需从栈中取出两个元素进行运算，随后将得到的结果入栈
     */
    public int evalRPN(String[] tokens) {
        // 定义栈用作操作辅助
        Stack<Integer> stack = new Stack<>();
        // 遍历表达式
        for (String token : tokens) {
            // 如果是操作数
            if ("+".equals(token) || "-".equals(token) || "*".equals(token) || "/".equals(token)) {
                // 取出栈元素
                int right = stack.pop();
                int left = stack.pop();
                int res;
                switch (token) {
                    case "+": {
                        res = left + right;
                        stack.push(Integer.valueOf(res));
                        break;
                    }
                    case "-": {
                        res = left - right;
                        stack.push(Integer.valueOf(res));
                        break;
                    }
                    case "*": {
                        res = left * right;
                        stack.push(Integer.valueOf(res));
                        break;
                    }
                    case "/": {
                        res = left / right;
                        stack.push(Integer.valueOf(res));
                        break;
                    }
                }
            } else {
                // 其他内容，数字处理直接压栈
                stack.push(Integer.valueOf(token));
            }
        }
        // 遍历完成，最终得到的栈中只有一个元素
        return stack.peek();
    }
}

复杂度分析
- 时间复杂度：O（n），n 为tokens数组长度
- 空间复杂度：O（n），借助辅助栈存储token元素

🔴05-基本计算器（224）（🚀）

1.题目内容

给你一个字符串表达式 s ，请你实现一个基本计算器来计算并返回它的值。

注意：不允许使用任何将字符串作为数学表达式计算的内置函数，比如 eval() 。

示例 1：

输入：s = "1 + 1"
输出：2

示例 2：

输入：s = " 2-1 + 2 "
输出：3

示例 3：

输入：s = "(1+(4+5+2)-3)+(6+8)"
输出：23

2.题解思路

👻方法1：栈

思路分析：借助栈存储字符串表达式中的数字（此处为了简化判断，将减去一个数转化为加上一个负数来实现）
- sign记录正负操作标记、tempRes记录临时保存的结果，遍历字符串表达式的字符
- 如果是数字：则需要得到一个完整的数字curVal（即往后遍历i+1位置字符，直到遇到非数字，将得到的序列组合成一个完整的数字），并将其累加到tempRes中
  - tempRes = tempRes + sign * curVal
- 如果是操作符号（+、-）：需更新sign标记（+：sign=1；-：sign=-1）
- 如果是括号：
  - 左括号(：临时结果入栈+重置 则说明需要将现有的临时记录压栈（暂时保存计算结果），然后进入括号中的表达式运算
    - 将当前的tempRes和sign入栈，然后重置这两个内容进入括号内表达式的计算
  - 右括号)：需弹出当前栈内临时保存的元素（tempRes和sign），然后更新操作结果：tempRes = prevNum + prevSign * tempRes
- 遍历结束，最终返回累加的结果集tempRes

/**
 * 224 基本计算器
 */
public class Solution1 {

    /**
     * 将操作转化为加法操作（减去一个数等价于加上一个负数）
     */
    public int calculate(String s) {
        // 使用栈存储字符串表达式的数字
        Stack<Integer> stack = new Stack<>();
        // 定义正负标记
        int sign = 1; // 1 表示正数
        // 临时保存计算结果
        int tempRes = 0;

        // 遍历字符串表达式，然后进行解析
        int len = s.length();
        for (int i = 0; i < len; i++) {
            char cur = s.charAt(i);
            // 判断当前字符
            if (Character.isDigit(cur)) {
                int curVal = Integer.valueOf(cur - '0'); // 需要将字符转数字
                // 如果是数字，则需判断其后一位是否存在（直到遇到非数字），组成一个完整的数字
                while (i + 1 < len && Character.isDigit(s.charAt(i + 1))) {
                    // 拼接更新当前的数字
                    curVal = curVal * 10 + Integer.valueOf(s.charAt(i + 1) - '0');
                    // 计算完成，i 继续往前
                    i++;
                }
                // 将结果进行累加
                tempRes = tempRes + sign * curVal;
            } else if (cur == '+' || cur == '-') {
                // 如果是+/-符号，则需更新sign
                sign = (cur == '+') ? 1 : -1; // sign=1 表示加一个正数,sign = -1 表示加一个负数
            } else if (cur == '(') {
                // 如果遇到左括号，则需先将前面的累计结果和符号状态入栈并初始化一个新的res和sigh标记用于计算括号内表达式的值
                stack.push(tempRes);
                stack.push(sign);
                // 初始化
                tempRes = 0;
                sign = 1;
            } else if (cur == ')') {
                // 如果遇到右括号，则说明需要将栈中的元素取出然后进行计算(先取出符号，后取出上一个操作数)
                int prevSign = stack.pop();
                int prevNum = stack.pop();
                // 更新结果值
                tempRes = prevNum + prevSign * tempRes;
            }
        }
        // 最终返回结果值
        return tempRes;
    }
}

复杂度分析
- 时间复杂度：O（n） n为字符串表达式长度
- 空间复杂度：O（n）借助栈存储操作数
案例分析：10+(5+20)-(1-3)
- 遍历字符串表达式中的元素内容：初始化tempRes=0、sign=1
- i=0：数字判断，则继续往后找到一个完整的数字10，然后累加到tempRes
  - tempRes => 10
- i=2：操作符号判断，更新sign
  - sign => 1
- i=3：左括号，需将当前的临时结果和操作符压栈，并重置tempRes \ sign
  - stack => 10 1
  - tempRes => 0、sign = 1
- i=4：数字判断，得到完整数字5，累加到tempRes
  - tempRes => 5
- i=5：操作符号判断，更新sign
  - sign => 1
- i=6：数字判断，得到完整数字20，累加到tempRes
  - tempRes => 25
- i=8：右括号，取出目前栈的元素，进行累加操作
  - stack => 空
  - tempRes => 35（10 + 1 * 25）
- i=9：操作符号判断，更新sign
  - sign => -1
- i=10：左括号，需将当前的临时结果和操作符压栈，并重置tempRes \ sign
  - stack => 35 -1
  - tempRes => 0、sign = 1
- i=11：数字判断，得到完整数字1，累加到tempRes
  - tempRes => 1
- i=12：操作符号判断，更新sign
  - sign => -1
- i=13：数字判断，得到完整数字1，累加到tempRes
  - tempRes => -2（tempRes = tempRes + sign * curVal）
- i=14：右括号，取出目前栈的元素，进行累加操作
  - stack => 空
  - tempRes => 35（35 + (-1) * -2）
- 遍历结束
  - 得到tempRes的值为37

昵称

邮箱

网址

按正序
按倒序
按热度

hot150-07-栈

预览: