难度说明：🟢简单🟡中等🔴困难

hot150-03-滑动窗口

滑动窗口场景

🟡01-长度最小的子数组（209）

1.题目内容

给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其总和大于等于 target 的长度最小的

子数组

[numsl, numsl+1, ..., numsr-1, numsr] ，并返回其长度**。**如果不存在符合条件的子数组，返回 0 。

2.题解思路

👻方法1：暴力法

​ 思路分析：判断以每个元素为起点的子数组的总和是否大于等于target，更新min

• 此处需注意子数组的总和计算可以不需要每次都计算[i,j]，每次循环通过累加的方式去实现即可
• 每次循环的是否判断当前子数组的累加和是否满足条件，满足则记录min

/**
 * 209 长度最小的子数组
 */
public class Solution1 {
    /**
     * 暴力法
     */
    public int minSubArrayLen(int target, int[] nums) {

        // 定义满足条件的子数组的最小长度
        int min = Integer.MAX_VALUE;

        // 判断以每个元素为起点的子数组是否满足target，暴力遍历所有子数组
        for (int i = 0; i < nums.length; i++) {
            // 每次循环可以定义一个累加sum，不用每次都重复计算一遍
            int curSum = 0;
            for (int j = i ; j < nums.length; j++) {
                // 计算和
                curSum += nums[j];
                if (curSum >= target) {
                    min = Math.min(min, j - i+1); // 更新min
                }
            }
        }

        // 返回响应
        return min==Integer.MAX_VALUE?0:min ;
    }
}

• 复杂度分析

  • 时间复杂度：

  • 空间复杂度：

👻方法2：滑动窗口

• 思路分析：定义滑动窗口，存储满足条件的子数组
  • 滑动窗口：存储子数组，左侧收缩、右侧扩张
  • 左右指针移动：从起点开始初始化，right 指向当前要移入窗口的元素，left 指向窗口的左边界
    • （1）将当前right指向元素加入窗口
    • （2）判断窗口中的子数组之和是否大于等于target，如果满足条件则记录min，并逐步移出左侧元素直到curSum<target（为了确保子数组特性，只能从左侧慢慢剔出元素，才可能让新元素在下次循环中加进来）
    • （3）操作完成将right右移（此处right++放在最后是因为在步骤（2）中会用索引位置来计算窗口元素个数，因此为了避免影响将指针右移放在最后）

/**
 * 209 长度最小的子数组
 */
public class Solution2 {

    public int minSubArrayLen(int target, int[] nums) {
        // 定义滑动窗口存储元素
        // HashSet<Integer> set = new HashSet<Integer>();
        int min = Integer.MAX_VALUE;

        // 定义指针确定窗口边界（left左边界，right指向当前要加入的元素位置）
        int left = 0, right = 0, curSum = 0;

        while (right < nums.length) {
           // 将当前元素加入
            curSum += nums[right];
            // 判断数据是否大于target，如果大于则记录min，并从左侧移入数据，直到curSum<target
            while (curSum >= target) {
                // 记录min
                min = Math.min(min,right - left + 1);
                // 从左侧逐步移出数据
                curSum -= nums[left];
                left++;
            }
            // right指向下一个元素(因为在while判断中会用到right，因此这个过程中要将right的变化放到最后，避免产生影响)
            right ++;
        }

        // 返回结果
        return min == Integer.MAX_VALUE ? 0 : min;
    }
    
}

• 复杂度分析

  • 时间复杂度：

  • 空间复杂度：

🟡02-无重复字符的最长子串（3）

1.题目内容

给定一个字符串 s ，请你找出其中不含有重复字符的 最长 子串 的长度

2.题解思路

👻方法1：

• 思路分析
  • 【1】定义一个滑动窗口，这个滑动窗口用于存放无重复子串（滑动过程中窗口大小会随之改变）
  • 【2】当滑动窗口的左右指针都走到字符串尾部时遍历结束，在这个过程中窗口会不断变化
    • 定义set存储滑动窗口的元素
    • 以left收缩、right扩张，当left、right 都到尾部则结束
      • right指向当前要加入窗口的元素cur，如果窗口中不包括cur，则将cur加入窗口，right向前滑动继续扩展
      • left指向左边界，如果判断当前窗口包括了cur，则需要移动左边界逐步将这个重复的元素移出
      • 在遍历操作的过程中需要记录窗口的最大值max

/**
 * 03 无重复字符的最长子串
 */
public class Solution1 {
    /**
     * 滑动窗口
     */
    public int lengthOfLongestSubstring(String s) {
        // 定义参数记录最大窗口
        int max = 0;
        // 定义一个滑动窗口
        HashSet<Character> set = new HashSet<>();
        // 定义滑动窗口的开始和结束索引
        int left = 0, right = 0;
        // 遍历目标字符串，根据规则滑动窗口(确认是否要将字符加入窗口),窗口滑到字符串右侧则结束
        int n = s.length();
        while (right < n) { // left < n && right < n
            // 当前校验的字符（以右指针为参考）
            char curChar = s.charAt(right); // 注意字符类型处理（此处用char接收处理字符串中的每个字符）
            // 判断字符是否已在集合中
            if (!set.contains(curChar)) {
                // 如果字符不在窗口中则说明当前字符可加入窗口，并将right指向下一个字符进行判断
                set.add(curChar);
                right++;
            } else {
                // 如果字符在窗口中，逐步将重复的元素移出
                set.remove(s.charAt(left));
                left++;
            }
            // 更新滑动窗口的最大值
            max = Math.max(max, set.size());
        }
        // 返回最大的内容
        return max;
    }
}

​ 以pwwkew为例，初始化left、right都指向第1个元素：

• 【1】p不在窗口内，则将其移入set，right后移指向下一位w，窗口更新为p

• 【2】w不在窗口内，则将其移入set，right后移指向下一位w，窗口更新为pw

• 【3】w在窗口中，则需将左边界元素逐步移出（目的是逐步将当前重复元素给移出），因此将p移出set，left后移指向w，窗口更新为w

• 【4】此时right当前指向的w仍在窗口中，类似地，将当前left指向的w移出，随后窗口更新为空窗口

• 【5】执行完步骤【4】后，继续判断发现w不在窗口内，则将其移入set，right后移指向下一位k，窗口更新为w

• 【6】k不在窗口内，则将其移入set，right后移指向下一位e，窗口更新为wk

• 【7】e不在窗口内，则将其移入set，right后移指向下一位w，窗口更新为wke

• 【8】w在窗口中，将当前left指向的w移出set，left后移指向k，窗口更新为kew

• 在整个遍历的过程中，记录窗口变化的最大值，返回返回这个长度即可，其核心和注意点在于：

  • 构建窗口：用于存储不重复的子串，通过left、right来限定窗口边界

  • left收缩、right扩展：right 指向当前要加入窗口的元素，通过判断这个元素是否存在于窗口来决定这个窗口是收缩还是扩展

    • 如果set不包括cur，则将cur加入set，right向右扩展
    • 如果set包括cur，则理论上需要将cur移出，然后等下一次遍历会将这个重复元素加入进来。因为设定是子串，因此不可以直接将cur移出（要确保窗口内的序列是子串概念），而是通过将left逐步收缩的方式，直到将这个重复元素移出，然后再下一次遍历的时候就可以将right指向元素加入进来了
    • 在整个遍历过程中需要记录这个窗口的变化大小，取max

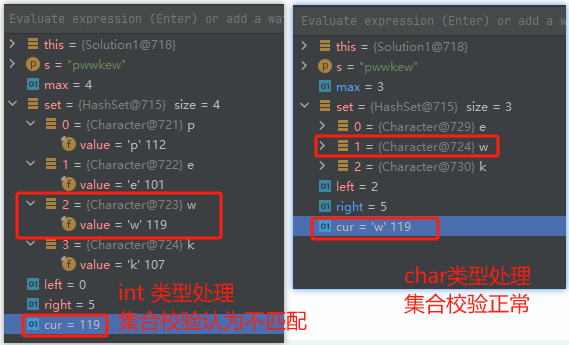
  • char和int：在用Set<Character>定义set集合时，处理字符串中的每个字符，需要用char类型匹配（否则由于自动类型转化机制可能导致一些校验出错）

    • 以pwwkew为例，如果用int类型接收处理字符串的每个字符，会自动将其转化为int类型（w=>119），当使用Set<Character>类型的集合去校验时就会发现set会认为这两个元素不是同一个内容（不匹配），显然不符合题意。那么最终运行的结果实际上统计的是字符串s去重的长度（会遍历所有元素，然后匹配校验认为遍历字符都不在现有的set集合中，就会直接执行加入操作，而set本身会做去重操作，所以最终得到的是去重后的s的长度，也就是4）
    • 正常用char类型处理，两边比较的类型匹配，所以可以正常执行相应的逻辑（可以通过打断点去处理）

    

• 复杂度分析

  • 时间复杂度：O（n）遍历所有元素

  • 空间复杂度：O（1）定义双指针辅助遍历（left 缩边、right 扩边）

双指针思路的另一种写法：

/**
     * 滑动窗口：定义滑动窗口存储不含重复字符的最长子串
     */
    public int lengthOfLongestSubstring(String s) {
        // 定义最长不重复子串长度
        int max = 0;
        // 构建集合存储不重复字符子串:left,right分别指向这个子串的左右边界（left缩边、right扩边）
        HashSet<Character> set = new HashSet<>();
        // 定义双指针
        int left = 0, right = 0;
        // 当right指针滑动到字符串尾部则结束（此处求的是最长子串，当right移动到字符串尾部遍历结束，因为剩下的情况就是left缩边，长度只会越来越小）
        while (right < s.length()) {
            // right用于扩展搜索，指向当前遍历元素位置，判断是否已经出现在set中
            char cur = s.charAt(right); // 注意用字符类型处理字符串中的每个字符
            if (!set.contains(cur)) {
                // 如果指向元素不在集合中则加入集合并更新最长不重复子串的长度
                set.add(s.charAt(right));
                right++;
                // 更新集合大小
                max = Math.max(max, set.size());
            } else {
                /**
                 * 如果指向元素已在集合中则需逐步移出前面出现这个重复元素及在其前面的元素，此处有两种思路处理
                 * ① 逐步移除：当出现重复元素时，每次从左侧移除一个元素（这个思路处理的核心在于每次校验只要set存在重复元素，就逐步从左侧开始缩边移除一位直到把满足加入新的元素并更新）
                 * ② 遍历移除：当出现重复元素时，从左侧开始搜索到这个重复的元素并移除，在遍历的过程中需要将搜索过的元素也一并移除
                 */
                while (s.charAt(left) != cur) { // 定位重复元素所在位置，并逐步移除前面的元素
                    set.remove(s.charAt(left));
                    left++;
                }
                set.remove(cur);  // 此处等价于 set.remove(s.charAt(left));
                left++;
            }
        }
        // 返回结果
        return max;
    }
}

🔴03-串联所有单词的子串（30）

1.题目内容

给定一个字符串 s 和一个字符串数组 words。 words 中所有字符串 长度相同。

s 中的 串联子串 是指一个包含 words 中所有字符串以任意顺序排列连接起来的子串。

• 例如，如果 words = ["ab","cd","ef"]， 那么 "abcdef"， "abefcd"，"cdabef"， "cdefab"，"efabcd"， 和 "efcdab" 都是串联子串。 "acdbef" 不是串联子串，因为他不是任何 words 排列的连接。

返回所有串联子串在 s 中的开始索引。你可以以 任意顺序 返回答案

示例 1：

输入：s = "barfoothefoobarman", words = ["foo","bar"]
输出：[0,9]
解释：因为 words.length == 2 同时 words[i].length == 3，连接的子字符串的长度必须为 6。
子串 "barfoo" 开始位置是 0。它是 words 中以 ["bar","foo"] 顺序排列的连接。
子串 "foobar" 开始位置是 9。它是 words 中以 ["foo","bar"] 顺序排列的连接。
输出顺序无关紧要。返回 [9,0] 也是可以的。

示例 2：

输入：s = "wordgoodgoodgoodbestword", words = ["word","good","best","word"]
输出：[]
解释：因为 words.length == 4 并且 words[i].length == 4，所以串联子串的长度必须为 16。
s 中没有子串长度为 16 并且等于 words 的任何顺序排列的连接。
所以我们返回一个空数组。

示例 3：

输入：s = "barfoofoobarthefoobarman", words = ["bar","foo","the"]
输出：[6,9,12]
解释：因为 words.length == 3 并且 words[i].length == 3，所以串联子串的长度必须为 9。
子串 "foobarthe" 开始位置是 6。它是 words 中以 ["foo","bar","the"] 顺序排列的连接。
子串 "barthefoo" 开始位置是 9。它是 words 中以 ["bar","the","foo"] 顺序排列的连接。
子串 "thefoobar" 开始位置是 12。它是 words 中以 ["the","foo","bar"] 顺序排列的连接。

2.题解思路

​ 参考题解

👻方法1：滑动窗口（滑动、分段截取比较）

• 思路分析：抓住题目核心单词等长
  • 外层遍历：定义一个固定长度的窗口（每个单词等长，则窗口长度为单词数量*单词长度），每次遍历都去判断这个窗口是否满足条件（即窗口元素是否满足串联子串的要求）
  • 内层循环：即如何判断这个窗口是否为串联子串，实际就是将字符串切割成n等分（n为单词个数），随后将其一一匹配单词列表中的数据
    • 例如窗口被划分为n个subStr，可以定义List存储单词，判断每个subStr是否存在于list中，存在则移除，如果不存在则说明不符合串联子串；当次窗口遍历完成需要复原List用于下次遍历判断使用
    • 同理，此处可以用Map来进行替代：key存储单词，value存储单词出现次数，如果单词不存在或者单词出现次数为0则说明不匹配

// 存在超时情况
public class Solution2 {

    /**
     * 分析：滑动窗口
     * 外层循环：定义一个固定的滑动窗口（窗口大小：单词个数*单词长度，因为单词是等长的）
     * 内存循环：目的是为了判断每个滑动窗口的数据是否为串联子串
     * - 定义一个集合存储单词（可重复集合）（因为此处每次判断都会移出集合元素，因此在循环中重建、移出） // todo 注意遍历集合移出集合元素的处理问题
     * - 将滑动窗口中的子串拆分为n（n为单词个数）部分，判断每个部分是否存在于集合中，存在则移除，不存在则说明不符合子串要求（直到所有子串判断完成）
     * 此处这个List也可用Map替代：key存储单词元素，value存储出现次数（当subStr不在这个Map中或者key对应value为0则说明不匹配）
     */
    public List<Integer> findSubstring(String s, String[] words) {
        // 定义结果接
        List<Integer> res = new ArrayList<>();

        // 计算滑动窗口大小
        int len = words[0].length() * words.length;
        // 定义一个滑动窗口（起始指针）
        int start = 0, end = len;

        // 外层循环(因为窗口有固定长度，此处只需要遍历到sLen-len的位置即可)
        for (int i = 0; i <= s.length() - len; i++) {
            String target = s.substring(start, end);
            // 判断target是否满足串联子串要求,满足将当前索引位置记录下来
            if(isValid(target, words)) {
                res.add(start);
            }
            // 本次遍历判断结束，指针继续向前
            start++;
            end++;
        }

        // 返回结果
        return res;
    }

    public boolean isValid(String target, String[] words) {
        // 1.将words放到一个集合中便于处理（此处用Map存储：key存储单词内容，value存储单词出现次数）
        Map<String,Integer> map = new HashMap<>();
        for(String word : words) {
            map.put(word, map.getOrDefault(word, 0) + 1);
        }

        // 2.将target拆分为words数组大小的n个部分
        int singleWordLen = words[0].length();
        int wordsLen = words.length;
        List<String> targetList = new ArrayList<>(wordsLen);
        for (int i = 0; i < target.length(); i = i + singleWordLen) {
            targetList.add(target.substring(i, i + singleWordLen)); // 每次截取单词长度的大小，截取完成i继续前进（步长为单词长度大小）
        }

        // 3.循环遍历目标集，校验是否匹配
        for(String str : targetList) {
            // 判断str是否存在于list中，存在则移除
            if(map.containsKey(str) && map.get(str) > 0) {
                map.put(str, map.get(str) - 1); // 将元素出现次数-1（表示这个单词用过了，等价于list移出元素）
            }else{
                // 不存在则说明不符合子串要求
                return false;
            }
        }
        return true;
    }
}

• 复杂度分析

  • 时间复杂度：

  • 空间复杂度：

3.复盘

// 3.循环遍历目标集，校验是否匹配
for(String str : targetList) {
    // 判断str是否存在于list中，存在则移除
    if(list.contains(str)) {
        list.remove(str);
    }else{
        // 不存在则说明不符合子串要求
        return false;
    }
}

​ 这段代码的处理逻辑问题在于不能在list判断的移出元素，因此此处要么拆两个list（一个只读，一个记录），要么借助Map来存储（记录单词元素的出现次数变化，而不真正移出元素）

🔴04-最小覆盖子串（76）todo

1.题目内容

2.题解思路

👻方法1：

• 复杂度分析

  • 时间复杂度：

  • 空间复杂度：