hot100-08-二叉树
难度说明:🟢简单🟡中等🔴困难
hot100-08-二叉树
技巧说明
- 核心掌握二叉树的遍历方式(DFS、BFS),大部分题型基于这两个思路进行展开
🟢01-二叉树的中序遍历(94)
1.题目内容
给定一个二叉树的根节点 root ,返回 它的 中序 遍历
2.题解思路
DFS:深度优先遍历参考思路
// 前序遍历
public static List<Integer> preOrder(TreeNode root,List<Integer> list){
// 判断当前节点是否为空
if(root == null){
return list;
}
// root->left->right
list.add(root.val);
preOrder(root.left, list);
preOrder(root.right, list);
return list;
}
// 中序遍历
public static List<Integer> midOrder(TreeNode root,List<Integer> list){
// 判断当前节点是否为空
if(root == null){
return list;
}
// left->root->right
midOrder(root.left, list);
list.add(root.val);
midOrder(root.right, list);
return list;
}
// 后序遍历
public static List<Integer> postOrder(TreeNode root,List<Integer> list){
// 判断当前节点是否为空
if(root == null){
return list;
}
// left->right->root
postOrder(root.left, list);
postOrder(root.right, list);
list.add(root.val);
return list;
}
// 初始化传入空List(list存储的是遍历的次序)
👻方法1:递归法
此处由于限定了只接受一个TreeNode参数,因此需要自己封装中序遍历的方法,相当于将上述的解题思路拆分为两个方法进行操作
public class Solution {
/**
* 二叉树的中序遍历
* @param root
* @return
*/
public List<Integer> inorderTraversal(TreeNode root) {
// 定义集合存储遍历序列
List<Integer> list = new ArrayList<Integer>();
list = inorderHelper(root,list);
return list;
}
/**
* 定义中序遍历辅助方法
*/
public List<Integer> inorderHelper(TreeNode root,List<Integer> list){
// 定义节点指针
TreeNode cur = root;
// 判断是否为null(不为null则继续遍历子节点)
if (cur != null) {
// 中序遍历次序:left->root->right
inorderHelper(cur.left,list);
list.add(cur.val); // 遍历节点(将节点值加入列表)
inorderHelper(cur.right,list);
}
// 返回遍历后的序列
return list;
}
/* 二叉树节点类 */
class TreeNode {
int val; // 节点值
TreeNode left; // 左子节点引用
TreeNode right; // 右子节点引用
TreeNode(int x) {
val = x;
}
public TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
}
复杂度分析
- 时间复杂度:O(n),其中 n 为二叉树节点的个数。二叉树的遍历中每个节点会被访问一次且只会被访问一次
- 空间复杂度:空间复杂度取决于递归的栈深度,而栈深度在二叉树为一条链的情况下会达到 O(n) 的级别
👻方法2:迭代法
参考层次遍历的思路,依次入队出队进行迭代
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<Integer>();
Deque<TreeNode> stk = new LinkedList<TreeNode>();
while (root != null || !stk.isEmpty()) {
while (root != null) {
stk.push(root);
root = root.left;
}
root = stk.pop();
res.add(root.val);
root = root.right;
}
return res;
}
}
3.复盘
🟢02-二叉树的最大深度(104)
1.题目内容
给定一个二叉树 root ,返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数

2.题解思路
👻方法1:深度优先遍历思路
如果知道左右子树的最大深度l、r,则树的最大深度为max(l,r)+1,类似地,左右子树的最大深度又可以基于此公式进行计算,因此可以采用深度优先搜索的思路来计算二叉树的最大深度。先递归计算出左右子树的最大深度,选择较大值+1即可,递归在访问到空节点时退出
public int maxDepth(TreeNode root) {
// 递归访问到空节点的时候退出
if(root == null) {
return 0;
}else{
// 分别计算左右子树的深度
int leftDepth = maxDepth(root.left);
int rightDepth = maxDepth(root.right);
return Math.max(leftDepth, rightDepth) + 1;
}
}
复杂度分析
时间复杂度:O(n),其中 n 为二叉树节点的个数。每个节点在递归中只被遍历一次
空间复杂度:O(height),其中 height 表示二叉树的高度。递归函数需要栈空间,而栈空间取决于递归的深度,因此空间复杂度等价于二叉树的高度
👻方法2:广度优先遍历思路
此处使用的是Deque双端队列,BFS遍历方式应采用队列的属性,先进先出
对比BFS遍历,如果是普通遍历节点,则直接进一个出一个进行统计即可,但是对于树的最大深度遍历,需要计算的是层数,因此要排除掉同层的元素统计(即每次出队前先获取当前的队列长度,将同层元素的遍历作为一个周期进行统计,进而得到树的最大深度)
// 广度优先遍历思路
public int maxDepthBFS(TreeNode root) {
// 定义节点深度
int depth = 0;
// 定义队列做遍历辅助
Deque<TreeNode> queue = new LinkedList<>();
queue.offer(root); // 初始化队列
while (!queue.isEmpty()) {
// 记录当前层的节点个数
int size = queue.size();
while(size>0){
TreeNode node = queue.poll();
if(node.left != null){
queue.offer(node.left); // 存入左节点
}
if(node.right != null){
queue.offer(node.right);// 存入右边节点
}
size--;
}
depth++;
}
return depth;
}

复杂度分析
时间复杂度:O(n),其中 n 为二叉树的节点个数。与方法一同样的分析,每个节点只会被访问一次
空间复杂度:此方法空间的消耗取决于队列存储的元素数量,其在最坏情况下会达到 O(n)
🟢03-翻转二叉树(226)
1.题目内容
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点
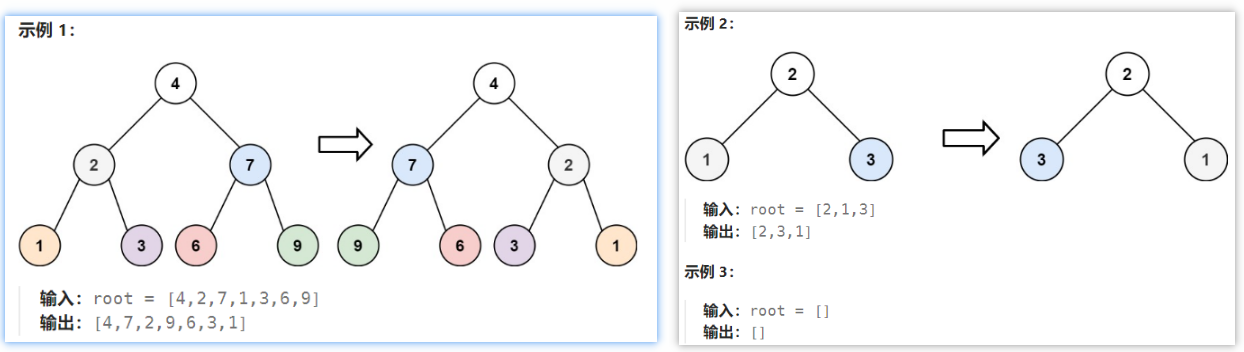
2.题解思路
👻方法1:递归
// 递归方式反转二叉树
public TreeNode invertTree(TreeNode root) {
// 空节点不做处理
if(root == null){
return null;
}
// 交换左右子树
TreeNode temp = root.left;
root.left = root.right;
root.right = temp;
// 递归交换左右子树的子节点
invertTree(root.left);
invertTree(root.right);
// 返回响应结果
return root;
}
复杂度分析
时间复杂度:O(N),其中 N 为二叉树节点的数目。我们会遍历二叉树中的每一个节点,对每个节点而言,在常数时间内交换其两棵子树
空间复杂度:O(N),使用的空间由递归栈的深度决定,它等于当前节点在二叉树中的高度。在平均情况下,二叉树的高度与节点个数为对数关系,即 O(logN)。而在最坏情况下,树形成链状,空间复杂度为 O(N)
👻方法2:层次遍历反转
// 层序遍历反转(相当于每次遍历节点的时候就将其左右节点进行交换)
public TreeNode invertTree(TreeNode root) {
// 空节点判断
if (root == null) {
return null;
}
Deque<TreeNode> queue = new LinkedList<>();
queue.offer(root);
// 遍历队列
while (!queue.isEmpty()) {
// 依次出队反转
TreeNode node = queue.poll();
// 将当前节点的左右节点进行反转
TreeNode temp = node.left;
node.left = node.right;
node.right = temp;
// 如果存在左右节点则继续入队
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
}
// 返回遍历、反转后的节点信息
return root;
}
复杂度分析
时间复杂度:
空间复杂度:
🟢04-对称二叉树(101)
1.题目内容
给你一个二叉树的根节点 root , 检查它是否轴对称
2.题解思路
👻方法1:递归思路
理解轴对称的概念:以根节点为中间轴,轴对称满足两个条件:
- 左右两个节点的val一致
- 每个树的右子树和另一个树的左子树镜像对称
采用"双指针"概念,定义两个指针分别进行游走,一开始初始化p、q都指向root,随后分别向相反方向遍历,检查任意时刻p、q指针指向的节点值是否相等,如果相等则继续遍历其左右子树是否对称
public boolean isSymmetric(TreeNode root) {
// p、q的起始节点均从root开始
return check(root,root);
}
public boolean check(TreeNode p, TreeNode q) {
// 边界条件检验
/* 如果p、q都为null */
if (p == null && q == null) {
return true;
}
/* 如果p、q两者中有一个为null,明显不符合镜像对称要求 */
if (p == null || q == null) {
return false;
}
/* p、q都不为null,需校验指针对应的节点值,及其子树的值(子树对称可通过递归校验) */
// if (p != null && q != null) {}
return p.val==q.val && check(p.left, q.right) && check(p.right, q.left);
}
复杂度分析
时间复杂度:遍历了这棵树,渐进时间复杂度为 O(n)
空间复杂度:空间复杂度和递归使用的栈空间有关,这里递归层数不超过 n,故渐进空间复杂度为 O(n)
🟢05-二叉树的直径(543)
1.题目内容
给你一棵二叉树的根节点,返回该树的 直径 。
二叉树的 直径 是指树中任意两个节点之间最长路径的 长度 。这条路径可能经过也可能不经过根节点 root 。
两节点之间路径的 长度 由它们之间边数表示

2.题解思路
👻方法1:深度遍历思路
结合题目描述分析,如果要获取二叉树中任意两个节点的最大直径,则需要观察哪两个节点是最值得计算的?
以3个节点的二叉树为例:leftNode左子节点、rootNode根节点、rightNode右子节点,基于此计算最大直径:可能的最大直径 = leftNode到rootNode的距离(lrd) + rootNode到rightNode的距离(rrd),那么如何让这个lrd和rrd之和倾向最大则可得到max
如果说二叉树不限于这3个节点,当节点很多的情况下,二叉树的层级会越来越深,据此可以观察到,只要找到lrd+rrd的最大值即可,基于此回归深度遍历计算树的最大深度概念,在递归的过程就就去计算lrd+rrd的最大值
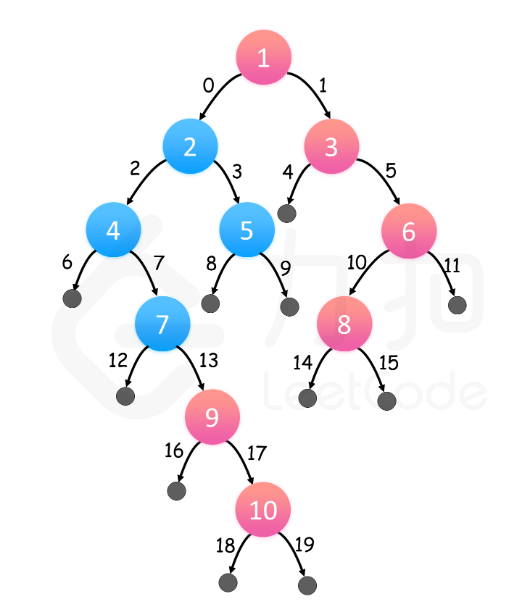
误区分析:此处可能存在一个容易出错的地方,结合上述公式分析,可能会误认为经过root的路径是最大的,所以将思路转向计算root的左右子树的最大深度之和,但实际上这个任意节点之间的最大直径可能并不会经过root(例如下述图示的节点参考)。因此此处的设定应该是当遍历到每个节点时,将其当做主节点记录下其左右子树的最大深度之和(即每个节点都有可能是上面的root角色),因此在迭代过程中就依次去对比lrd+rrd的最大值,然后所有节点遍历结束得到一个max
参考下述图示,如果基于图示代码拆分为左右子树(经过root)则得到最大值是1+6=7,而实际上当不经过root时有一条路径能得到8
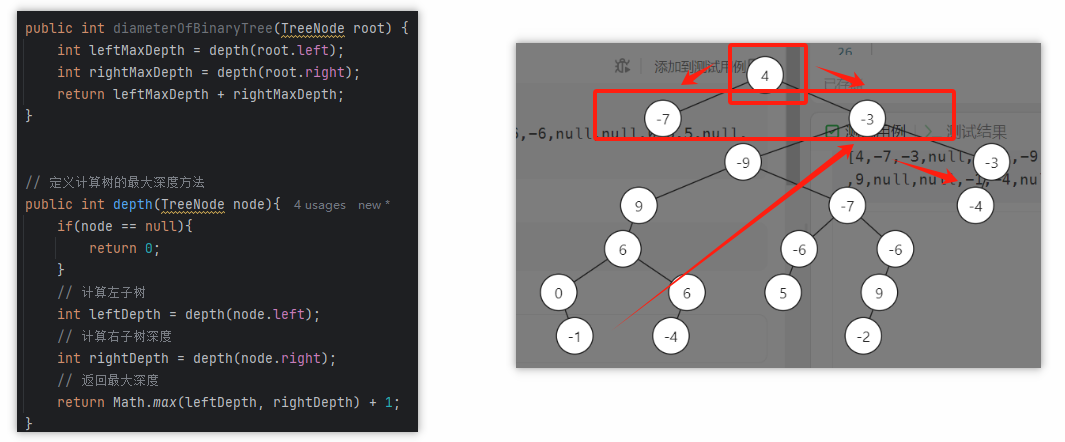
因此此处深度遍历核心就是:依次遍历每个节点,将每个节点当做当前的子树root,然后调用depth递归方法获取左右子树的最大深度,并更新lrd+rrd的最大值
// 定义直径
int diameter = 0;
public int diameterOfBinaryTree(TreeNode root) {
depth(root);
return diameter;
}
// 定义计算树的最大深度方法
public int depth(TreeNode node){
if(node == null){
return 0;
}
// 计算左子树
int leftDepth = depth(node.left);
// 计算右子树深度
int rightDepth = depth(node.right);
// 更新最大值
diameter = Math.max(diameter, leftDepth + rightDepth);
// 返回最大深度
return Math.max(leftDepth, rightDepth) + 1;
}
复杂度分析
时间复杂度:
空间复杂度:
3.复盘
🟡06-二叉树的层序遍历(102)
1.题目内容
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)
2.题解思路
👻方法1:层序遍历(借助队列辅助操作)
此处注意结果集的处理,分层进行操作,因此需要记录每一层操作的节点数,每一层的操作作为一个周期记录
public List<List<Integer>> levelOrder(TreeNode root) {
// 定义结果集
List<List<Integer>> res = new ArrayList<List<Integer>>();
if (root == null) {
return new ArrayList<>();
}
// 定义队列进行辅助操作
Deque<TreeNode> queue = new LinkedList<TreeNode>();
queue.offer(root); // 初始化队列
// 当队列不为空则迭代队列
while (!queue.isEmpty()) {
// 记录当前队列节点(分层遍历)
int n = queue.size();
List<Integer> curList = new ArrayList<>();
while (n > 0) {
// 节点依次出队处理,并将其左右节点加入队列等待下层处理
TreeNode cur = queue.poll();
curList.add(cur.val); // 将节点值存入遍历序列
// 判断当前节点是否存在左右节点
if (cur.left != null) {
queue.offer(cur.left); // 左节点入队处理
}
if (cur.right != null) {
queue.offer(cur.right); // 右节点入队处理
}
n--;
}
// 完成一层遍历,将列表加入结果集
res.add(curList);
}
return res;
}
复杂度分析
- 时间复杂度:
- 空间复杂度:
🟢07-将有序数组转为二叉搜索树(108)
1.题目内容
给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵 平衡 二叉搜索树
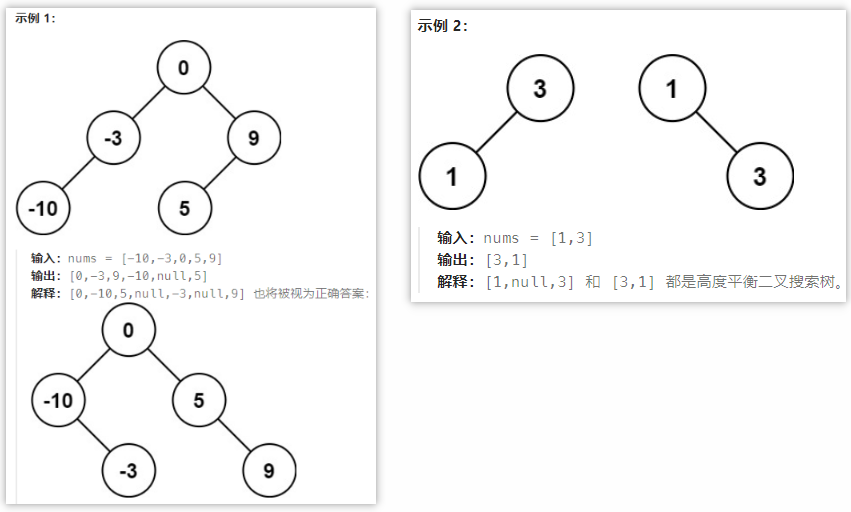
2.题解思路
👻方法1:中序遍历逆向思考
在树的学习中有cue到二叉搜索树的中序遍历是升序序列,此处给定的数组是按照升序排序的有序数组,因此可以确保数组是二叉搜索树的中序遍历序列。以这个为切入点,反向构建相应的二叉搜索树,但仅仅通过中序遍历是没有办法唯一确定一个二叉搜索树的
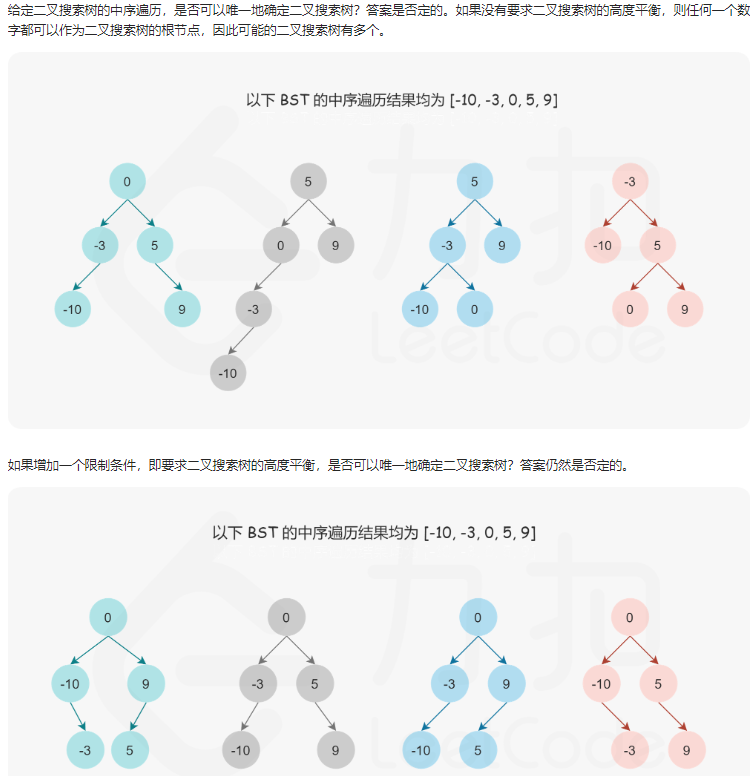
此处将中点作为根节点,中点左侧作为左子树,右侧作为右子树
// 数组本身有序,将中点作为根节点,中点左侧的作为左子树、中点右侧的作为右子树
public TreeNode sortedArrayToBST(int[] nums) {
// 判断传入的nums长度是否为0,如果为0则不需要构建
if(nums == null || nums.length == 0) {
return null;
}
// 计算中点
int mid = nums.length / 2;
// 创建根节点进行存储
TreeNode root = new TreeNode(nums[mid]);
root.left = sortedArrayToBST(Arrays.copyOfRange(nums,0,mid)); // 将数组左边的元素作为左节点
root.right = sortedArrayToBST(Arrays.copyOfRange(nums,mid+1,nums.length)); // 将数组右边的元素作为右节点
// 返回root
return root;
}
复杂度分析
时间复杂度:
空间复杂度:
PS:还有一种硬核方式就是手撕AVL代码的新增节点方法(涉及树的旋转),然后依次遍历数组进行插入即可
🟡08-验证二叉搜索树(98)
1.题目内容
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
节点的左
子树
只包含
小于
当前节点的数。
节点的右子树只包含 大于 当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。
2.题解思路
👻方法1:二叉搜索树的中序遍历是升序序列
/**
* 98.二叉搜索树验证
*/
public class Solution1 {
public boolean isValidBST(TreeNode root) {
// 二叉搜索树的中序遍历是升序的,因此可以基于此先得到二叉搜索树的中序遍历序列,然后校验升序性
List<Integer> list = toBFS(root);
// 校验list的升序性(相邻两个元素依次比较)
for(int i=0;i<list.size();i++){
for(int j=i+1;j<list.size();j++){
if(list.get(i)>=list.get(j)){ // 需注意数组元素重复的情况,二叉搜索树不允许出现重复值
return false;
}
}
}
return true;
}
public List<Integer> toBFS(TreeNode root) {
List<Integer> list = new ArrayList<Integer>();
list = bfs(root,list);
return list;
}
public List<Integer> bfs(TreeNode node,List<Integer> list) {
// 判断node是否为null,为null不执行操作
if(node == null){
return list;
}
// 中序遍历:left、root,right
bfs(node.left,list); // 左节点
list.add(node.val);
bfs(node.right,list);// 右节点
// 返回list
return list;
}
}
复杂度分析
- 时间复杂度:
- 空间复杂度:
3.复盘
🟡09-二叉搜索树中第K小的元素(230)
1.题目内容
给定一个二叉搜索树的根节点 root ,和一个整数 k ,请你设计一个算法查找其中第 k 小的元素(从 1 开始计数)
2.题解思路
👻方法1:二叉搜索树的中序遍历是升序序列
public int kthSmallest(TreeNode root, int k) {
List<Integer> list = toBFS(root);
return list.get(k-1);
}
// 构建二叉搜索树的中序遍历序列
public List<Integer> toBFS(TreeNode root) {
List<Integer> list = new ArrayList<>();
list = bfs(root,list);
return list;
}
public List<Integer> bfs(TreeNode node,List<Integer> list) {
// 判断node是否为null(为null不执行任何操作,直接返回)
if(node == null){
return list;
}
// 中序遍历操作:left->root->right
bfs(node.left,list); // 左节点
list.add(node.val); // root
bfs(node.right,list);// 右节点
// 返回列表(遍历序列)
return list;
}
复杂度分析
- 时间复杂度:
- 空间复杂度:
🟡10-二叉树的右视图(199)
1.题目内容
给定一个二叉树的 根节点 root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值
2.题解思路
思路1:基于深度优先遍历,每次先访问右子树,那么对于每层来说,在这层见到的第一个节点一定是最右边的节点
思路2:基于广度优先遍历(层次遍历),在分层遍历过程中,每次选择最后一个元素加入遍历序列即可
👻方法1:BFS(广度优先遍历)
基于BFS方式,在对每层遍历的时候,将当层的最后一个节点加入遍历序列
public List<Integer> rightSideView(TreeNode root) {
// 定义结果集
List<Integer> res= new ArrayList<>();
// NULL判断(根节点为null则返回空集合)
if(root==null){
return res;
}
// 定义辅助队列
Deque<TreeNode> queue = new LinkedList<TreeNode>();
queue.offer(root); // 初始化队列
// 依次遍历队列
while (!queue.isEmpty()) {
// 取节点依次出队(按照分层记录)
int size = queue.size(); // 存储每层的节点个数
for(int i = 0; i < size; i++) {
TreeNode node = queue.poll(); // 出队(读取节点)
// 判断当前节点是否为当前层的最后一个节点
if(i==size-1){
res.add(node.val); // 说明是符合右子树视图的条件
}
// 将当前节点的左右节点加入列表,等待下次循环
if(node.left!=null){
queue.offer(node.left);
}
if(node.right!=null){
queue.offer(node.right);
}
}
}
// 返回结果集
return res;
}
复杂度分析
- 时间复杂度:
- 空间复杂度:
🤡方法2:DFS(递归)
class Solution {
public List<Integer> rightSideView(TreeNode root) {
List<Integer> res = new ArrayList<>();
dfs(res, root, 0);
return res;
}
private void dfs(List<Integer> res, TreeNode node, int level) {
if(node != null) {
if(res.size() == level) {
res.add(node.val);
}
dfs(res, node.right, level + 1);
dfs(res, node.left, level + 1);
}
}
}
🟡11-二叉树展开为链表(114)
1.题目内容
给你二叉树的根结点 root ,请你将它展开为一个单链表:
- 展开后的单链表应该同样使用
TreeNode,其中right子指针指向链表中下一个结点,而左子指针始终为null。 - 展开后的单链表应该与二叉树 先序遍历 顺序相同

2.题解思路
👻方法1:基础思路
基于题意,按照下述方式的顺序执行操作:
- 【1】将左子树插入到右子树的地方
- 【2】将原来的右子树接到左子树的最右边节点
- 【3】考虑新的右子树的根节点,一直重复上边的过程,直到新的右子树为 null
1
/ \
2 5
/ \ \
3 4 6
//将 1 的左子树插入到右子树的地方
1
\
2 5
/ \ \
3 4 6
//将原来的右子树接到左子树的最右边节点
1
\
2
/ \
3 4
\
5
\
6
//将 2 的左子树插入到右子树的地方
1
\
2
\
3 4
\
5
\
6
//将原来的右子树接到左子树的最右边节点
1
\
2
\
3
\
4
\
5
\
6
public class Solution1 {
public void flatten(TreeNode root) {
/**
* 1.记录root的左右子树
* 2.将左子树left移动到右子树right的位置
* 3.然后将原来的右子树right移动到左子树最右边的节点
* 4.依次类推,直到左边的节点被全部移过去
*/
// 定义cur记录当前节点位置
TreeNode cur = root;
while (cur != null) {
// 1.记录当前节点的左右子树
TreeNode leftTree = cur.left;
TreeNode rightTree = cur.right;
// 如果左子树为空则直接进入下一个节点,不为空则进行移动操作
if (leftTree != null) {
// 2.将左子树移动到右子树的位置
cur.right = leftTree;
cur.left = null; // 原有的左节点位置置空
// 3.将原右子树移动到现在这个新的右子树最右边的节点(找出这个最右边节点)
TreeNode finder = leftTree;
while (finder.right != null) {
finder = finder.right;
}
finder.right = rightTree; // 将右子树移动到其右节点
}
// 更新cur指针位置(下一个指针指向当前节点的右节点)
cur = cur.right;
}
}
}
👻方法2:先序遍历
结合题目分析,展开后的单链表和二叉树先序遍历的顺序相同,最简单的一种思路就是先将二叉树先序遍历的序列敲定下来,然后基于此链表构造一条先序顺序的链表。但题目要求是使用原地算法(O(1)额外空间)展开这棵树
复杂度分析
- 时间复杂度:
- 空间复杂度:
3.复盘
🟡12-从前序和中序遍历序列构造二叉树(105)
1.题目内容
给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点
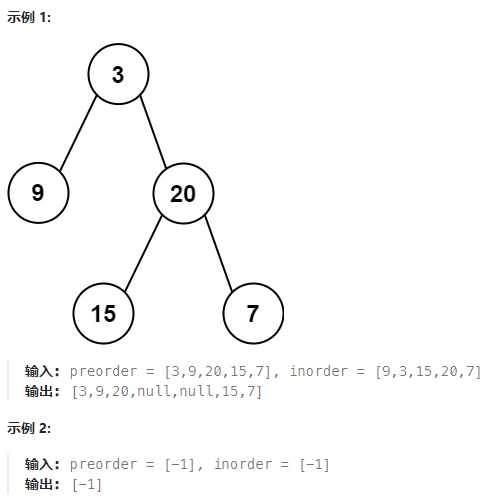
2.题解思路
中序遍历:left->root->right:中序遍历的第一个元素是left、最后一个元素是right,根节点左边的所有元素都在根节点左子树中,右边的所有元素都在根节点右子树中
前序遍历:root->left->right:前序遍历的第一个元素是根节点
👻方法1:分治法
【步骤1】:梳理序列的对照关系(根节点元素及位置,对应左右子树在各个序列的边界)
中序遍历(left->root->right):【【左子树的inOrder结果】,根节点,【右子树的inOrder结果】】
前序遍历(root->left->right):【根节点,【左子树的preOrder结果】,【右子树的preOrder结果】】
(1)根节点的确认:根据前序遍历的第一个元素确定根节点值,然后根据val在中序遍历中定位根节点的位置(索引)
(2)判断左右节点的个数(实际为定位根节点在中序序列的位置):确定了根节点的位置后,在中序遍历中根节点左边就是左子树的节点个数、根节点右边就是右子树的节点个数
(3)左右子树的构建:结合图示理解分析(通过划分数组的下限,定义不同的下标/游标实现编码),前序遍历的左右游标(preLeft、preRight),中序遍历的左右游标(inLeft、inRight)

数据的对应关系可以拆解为:(梳理每个序列的根节点位置,和对应左右子树的边界索引,确定两个序列的对照关系(即对应子树的元素))
以中序遍历为参考,其左侧是左子树的所有节点,这些节点在前序遍历中对应的位置是根据根节点下一个位置+子节点个数进行确定的
- 即中序遍历
[inLeft,pivot-1](左子树)对应前序遍历中[preLeft+1,preLeft+左子树节点个数],而左子树节点个数在中序遍历中可以通过pivot-inLeft得到 - 基于此分析左子树的关系映射为:中序的
[inLeft,pivot-1]元素 =[preLeft+1,preLeft+pivot-inLeft]元素
- 即中序遍历
同理继续基于此梳理右子树的游标关系:中序的
[pivot+1,inRight]元素=[preLeft+pivot-inLeft+1,preRight]元素
【步骤2】创建根节点并递归构建左右子树
左右子树的构建最终是落实到子节点的创建,因此基于上述关系分析,可进一步构造递归函数进行构建(首先就是确定递归函数的入参和出参),递归的结束条件就是边界相遇,基于前序遍历序列去构建,借助中序遍历序列确定子树节点个数
- (1)确定递归退出条件(基于前序遍历序列构建,当前序的两个边界相遇则退出,即
preLeft>preRight时return) - (2)正常创建根节点(递归的最终也是落实到单个节点的创建)并设置其相应的左右子树
- 此处结合图示进行理解,按照图示参数一步步拿到需要的值并设置
/**
* 105.从前序和中序遍历序列中构造二叉树
*/
public class Solution1 {
public TreeNode buildTree(int[] preorder, int[] inorder) {
TreeNode root = buildTreeHelper(preorder,inorder,0,preorder.length-1,0,inorder.length-1);
return root;
}
// 前序遍历序列、中序遍历序列、子树的前序左右边界(preLeft、preRight)、子树的中序左右边界(inLeft、inRight)
public TreeNode buildTreeHelper(int[] preorder, int[] inorder,int preLeft,int preRight,int inLeft,int inRight) {
// 基于前序遍历序列去构建,借助中序遍历序列确定左子树节点个数,如果左右边界相遇则结束
if(preLeft>preRight){
return null;
}
// 满足条件则递归构建子树(最终落实到创建节点)
// 1.确定根节点(前序序列的第一个元素)
TreeNode root = new TreeNode(preorder[preLeft]);
// 2.计算左子树的元素长度(leftCount = pivot-inLeft),其中pivot为根节点在中序遍历序列的下标索引(自定义工具方法获取)
// int leftCount = getRootIndex(root.val,inorder) - inLeft ;
int pivot = getRootIndex(root.val,inorder) ; // 如果此处对照图示则an按照图示的参数定义便于理解,避免混淆
// 3.递归构建左右子树(结合图示设置值即可)
root.left = buildTreeHelper(preorder,inorder,preLeft+1,preLeft+pivot-inLeft,inLeft,pivot-1);// 对应传入左子树的前序左右边界和中序左右边界
root.right = buildTreeHelper(preorder,inorder,preLeft+pivot-inLeft+1,preRight,pivot+1,inRight);// 对应传入右子树的前序左右边界和中序左右边界
// 返回创建的节点信息
return root;
}
/**
* 根据val值获取其在对应数组的下标位置
* @param val
* @return
*/
private int getRootIndex(int val,int[] inorder){
for(int i=0;i<inorder.length;i++){
if(inorder[i]==val){
return i;
}
}
return -1;
}
}
基于上述优化方向,会从getRootIndex这个定位根节点位置的方法进行切入,先将inorder数组转为哈希表存储(map),提升数据快速检索定位效率,需注意的是,此处存储的是非重复元素
🟡13-路径总和III(437)
1.题目内容
给定一个二叉树的根节点 root ,和一个整数 targetSum ,求该二叉树里节点值之和等于 targetSum 的 路径 的数目。
路径 不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)

2.题解思路
👻方法1:深度优先搜索(双递归调用思路)
最基础的解法是穷举所有的可能,即访问每个节点node,检测以node为起始节点向下衍生的路径有多少种。递归遍历每个节点的所有可能的路径,然后将这些路径数目加起来
(1)根节点上的路径穷举等于当前节点的路径穷举+左子树的路径穷举+右子树的路径穷举,其中左右子树的路径穷举实际又可向下传递给各自的左右子树,基于此整体的计算框架可以同归递归来进行设计
(2)上述方法中左右子树可通过递归来进行计算,主要关注当前节点的路径穷举(通过定义方法
rootSum(TreeNode p)实现,表示以P为根节点,遍历其下的路径(遍历则可通过深度优先遍历来实现)),基于此可以设计下述大致的框架// 第1个递归(得到当前节点的所有可能路径) public int pathSum(TreeNode root) { if (root == null) { return 0; } int ret = rootSum(root); // 此处的rootSum(p)是为了以当前 ret += pathSum(root.left); // 左子树穷举 ret += pathSum(root.right);// 右子树穷举 return ret; }(3)由于路径的查找是为了判断是否存在路径和为target的值的路径,这点可以通过在遍历过程中计算得到,因此入参需要传入target在遍历过程中进行校验,则进一步调整方法设计
// 第1个递归(得到当前节点的所有可能路径) public int pathSum(TreeNode root,int targetNum) { if (root == null) { return 0; } int ret = rootSum(root,targetNum); // 此处的rootSum(p)是为了以当前 ret += pathSum(root.left,targetNum); // 左子树穷举 ret += pathSum(root.right,targetNum);// 右子树穷举 return ret; }(4)基于此,此处需进一步思考
rootSum(root,targetNum)方法的设计,其表示以节点p为起点向下且满足路径总和为targetNum的路径数目,这点可以在DFS遍历过程中进行校验
public int rootSum(TreeNode root, long targetSum) {
int ret = 0;
if (root == null) {
return 0;
}
// 判断特殊情况(如果自身节点满足也算一个有效的路径)
int val = root.val;
if (val == targetSum) {
ret++;
}
// 递归获取子树路径的统计
ret += rootSum(root.left, targetSum - val); // targetSum-val 表示子树需要凑出来的路径和
ret += rootSum(root.right, targetSum - val);
return ret;
}
参考代码
由于提供的测试用例累加会超过int阈值,所以此处要用long进行替换调整
public int pathSum(TreeNode root, int targetSum) {
// 1.穷举法概念:将当前节点的可能路径拆分为三部分进行计算:当前节点的路径穷举+左子树的路径穷举+右子树的路径穷举
if (root == null) {
return 0;
}
int res = 0;
int cur = rootSum(root, targetSum);
int left = pathSum(root.left, targetSum);
int right = pathSum(root.right, targetSum);
res += cur + left + right;
return res;
}
private int rootSum(TreeNode node, int targetSum) {
int res = 0;
if (node == null) {
return 0;
}
int val = node.val;
// 特殊情况考虑(如果当前节点值等于targetSum,则其本身就是一条满足条件的路径)
if (val == targetSum) {
res++;
}
// 递归计算左右子树
res += rootSum(node.left, targetSum - val) + rootSum(node.right, targetSum - val);// 此处设定target-val,表示向下传递的子树需要满足的路径和
// 返回结果
return res;
}
复杂度分析
- 时间复杂度:
- 空间复杂度:
🟡14-二叉树的最近公共祖先(236)
1.题目内容
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)
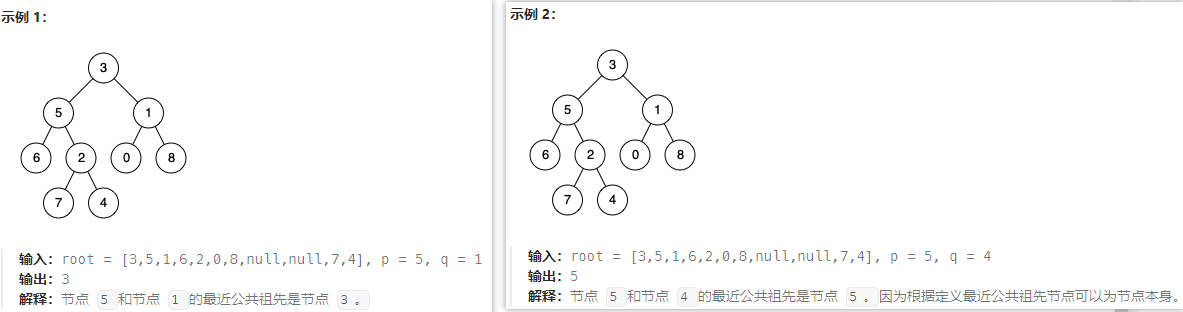
2.题解思路
👻方法1:
将寻找最近公共祖先拆分多种情况进行分析:采用递归的思路进行查找,核心思路
- 设定递归条件
- 判断最近公共祖先是否在当前节点(
node==p || node==q) - 判断最近公共祖先在左节点还是右节点
/**
* 236.最小公共路径
*/
public class Solution1 {
// 递归思路,如果在过程中找到满足条件的直接返回
public TreeNode lowestCommonAncestor(TreeNode node, TreeNode p, TreeNode q) {
// 递归退出条件
if(node==null){
return null;
}
// 如果当前节点为p或q,则当前节点即为最小公共节点
if(node==p || node==q){
return node;
}
// 将找公共路径的任务交给左右子树找
TreeNode findLeft = lowestCommonAncestor(node.left, p, q);
TreeNode findRight = lowestCommonAncestor(node.right, p, q);
// 判断左右子树是否找到,然后分情况讨论
if(findLeft!=null && findRight!=null){
// 左右子树都找到了,则说明公共节点就是当前节点
return node;
}
if(findLeft!=null){
// 只有左子树找到了
return findLeft;
}
if(findRight!=null){
// 只有右子树找到了
return findRight;
}
// 如果左右子树都没有找到
return null;
}
}
简化版本
public boolean dfs(TreeNode root, TreeNode p, TreeNode q){
if(root == null){
return false;
}
//在当前节点
boolean inCurrentNode = root.val == p.val || root.val == q.val;
//在左节点
boolean inLeft = dfs(root.left,p,q);
//在右节点
boolean inRight = dfs(root.right,p,q);
if((inLeft && inRight) || (inCurrentNode && (inLeft || inRight))){
ans = root;
}
return inLeft || inRight || inCurrentNode;
}
复杂度分析
- 时间复杂度:
- 空间复杂度:
