hot100-06-矩阵

holic-x...大约 4 分钟

难度说明：🟢简单🟡中等🔴困难

hot100-06-矩阵

🟡01-矩阵置零（73）

1.题目内容

给定一个 m x n 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。请使用 原地open in new window 算法

2.题解思路

👻方法1：标记法

循环遍历矩阵元素，如果当前的元素为0，则标记当前元素对应行、列为true，然后再次循环遍历矩阵根据标记进行置0操作

/**
 * 73.矩阵置零
 * 思路：标记置0操作
 */
public class Solution {

    public void setZeroes(int[][] matrix) {
        int rowLen = matrix.length;
        int colLen = matrix[0].length;

        // 定义置零的行、列标记（一维数组）
        boolean[] row = new boolean[rowLen];
        boolean[] col = new boolean[colLen];

        // 循环遍历矩阵，校验元素是否为0，为0则进行标记
        for(int i=0;i<rowLen;i++) {
            for(int j=0;j<colLen;j++) {
                if(matrix[i][j]==0) {
                    // 将对应行、列进行标记
                    row[i]=col[j]=true;
                }
            }
        }

        // 再次循环遍历矩阵，根据标记进行置零
        for(int i=0;i<rowLen;i++) {
            for(int j=0;j<colLen;j++) {
                if(row[i] || col[j]) {
                    matrix[i][j]=0;
                }
            }
        }
    }
}

扩展思路：将元素为0的索引位置记录下来，然后根据索引分别对行、列进行置零

复杂度分析

时间复杂度：
空间复杂度：

3.复盘

🟡02-螺旋矩阵（54）

1.题目内容

给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素

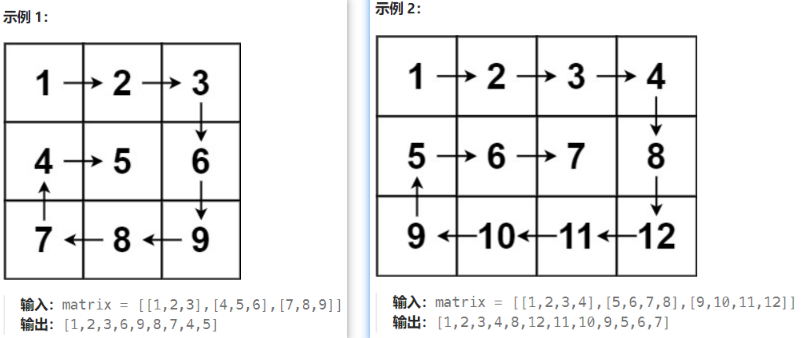
2.题解思路

👻方法1：4 个指针转圈圈

算法核心说明（m×n矩阵：[[1,2,3],[4,5,6]]这是一个3×2的矩阵 => m=matrix[0].length、n=matrix.length）
- 定义4个指针（边界），left=0（左边界）、right=m-1（右边界）、top=0（上边界）、bottom=n-1
- 按照4个方向依次进行遍历（即将当前索引指向的元素加入结果集），然后判断向哪边缩圈
- 从左到右遍历（left=>right）：遍历一遍当前top边界，随后top++（上边界下移）
- 从上到下遍历（top=>bottom）：遍历一遍当前right边界，随后right--（右边界左移）
- 从右到左遍历（right=>left）：当上下边界没有越界（避免重复读取），遍历一遍当前bottom边界，随后bottom--（下边界上移）
- 从下到上遍历（bottom=>top）：当左右边界没有越界（避免重复读取），遍历一遍完成当前left边界，随后left++（左边界右移）

依次类推，当边界相遇时停止检索（即当满足条件left<=right&&top<=bottom进行遍历，直到不满足条件遍历结束跳出循环。或者是res.size()<m×n（res.size()==m×n表示已经将当前矩阵所有元素塞入结果集了））

/**
 * 54.螺旋矩阵
 * 思路：四指针依次循环读取
 */
public class Solution {
    public List<Integer> spiralOrder(int[][] matrix) {

        // 定义结果集合
        List<Integer> list = new ArrayList<Integer>();

        // 矩阵大小(m*n)[[a,b,c],[a,b,c]] => 3*2
        int m = matrix[0].length, n = matrix.length;

        // 定义4个边界指针并初始化
        int left = 0, right = m - 1, top = 0, bottom = n - 1;

        // 循环遍历4个方向，当指针相遇时候遍历停止
        while(left <= right && top <= bottom) { // 或者是list.size < m * n(因为res.size()==m×n`表示已经将当前矩阵所有元素塞入结果集了)
            // 从左往右循环一遍（行不变），遍历完成top边界下移
            for(int i=left;i<=right;i++){
                list.add(matrix[top][i]);
            }
            top++;// top边界下移

            // 从上往下循环一遍（列不变），遍历完成right边界左移
            for(int i=top;i<=bottom;i++){
                list.add(matrix[i][right]);
            }
            right--;

            // 从右往左循环一遍（行不变），遍历完成左边界右移
            if(top<=bottom){
                for(int i=right;i>=left;i--){
                    list.add(matrix[bottom][i]);
                }
            }
            bottom--;

            // 从下往上循环一遍（行不变），遍历完成左边界右移
            if(left<=right){
                for(int i=bottom;i>=top;i--){
                    list.add(matrix[i][left]);
                }
            }
            left++;
        }

        // 返回结果集
        return list;

    }
}