hot150-08-链表
难度说明:🟢简单🟡中等🔴困难
hot150-08-链表
🟢01-环形链表(141)
1.题目内容
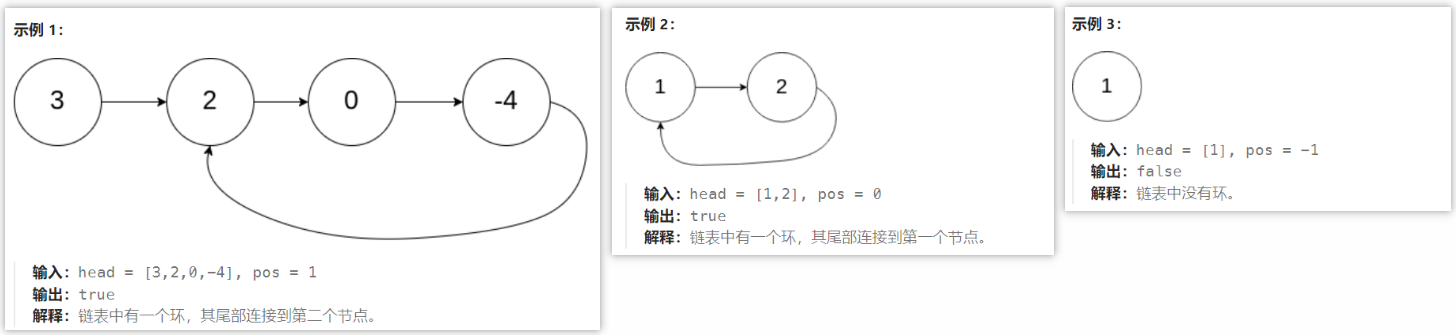
给你一个链表的头节点 head ,判断链表中是否有环。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。注意:pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。
如果链表中存在环 ,则返回 true 。 否则,返回 false 。
2.题解思路
👻方法1:哈希表
- 思路分析:遍历所有链表元素,并加入集合,如果此前集合中已经存在该元素则说明链表存在环
/**
* 141 环形链表
*/
public class Solution1 {
/**
* 判断链表中是否存在环
* 思路:哈希表
*/
public boolean hasCycle(ListNode head) {
// 定义集合存储链表元素,如果集合中存在重复元素则说明链表中存在环
Set<Integer> set = new HashSet<>();
ListNode point = head ; // 定义遍历指针
while(point!=null){
if(set.contains(point.val)){
// 集合中已存在该元素,说明存在环
return true;
}
// 将元素加入集合,指针后移
set.add(point.val);
point = point.next;
}
return false;
}
}
复杂度分析
时间复杂度:O(n) 遍历链表元素,n为链表长度
空间复杂度:O(n)需要set存储链表元素,最坏情况下不存在环,需要占用链表长度的空间存储元素
👻方法2:快慢指针法
- 思路分析:定义快慢指针遍历链表元素
- 快慢指针起点相同
- 慢指针走1步、快指针走2步:如果两者相遇则说明存在环;如果快指针先遍历到链表尾部则说明不存在环
/**
* 141 环形链表
*/
public class Solution2 {
/**
* 判断链表中是否存在环
* 思路:快慢指针
* 1.如果链表不存在环,则必然会遍历到链表尾部(也就是说快指针到达链表尾部的时候,就会跳出链表遍历了)
* 2.如果链表存在环,则快慢指针必然会相遇(因为存在环,快慢指针必然会在圈子内转圈圈,最终在某个时刻相遇)
*/
public boolean hasCycle(ListNode head) {
// 定义快慢指针:如果链表中存在环则快慢指针最终会相遇,如果不存在环则均能遍历到尾部
ListNode slow = head;
ListNode fast = head;
// 遍历元素
while (fast != null && fast.next != null) { // 如果快指针遍历到链表尾部则循环结束
// 快慢指针继续往前
slow = slow.next; // 慢指针走1步
fast = fast.next.next; // 快指针走2步
// 判断如果指针相遇,则说明存在环
if (slow == fast) {
return true;
}
}
return false;
}
}
复杂度分析
时间复杂度:O(n) n 链表节点数(最坏情况下需要遍历每个节点)
空间复杂度:O(1)定义了快慢指针,只占用了这两个指针的额外空间
🟡02-两数相加(02)
1.题目内容
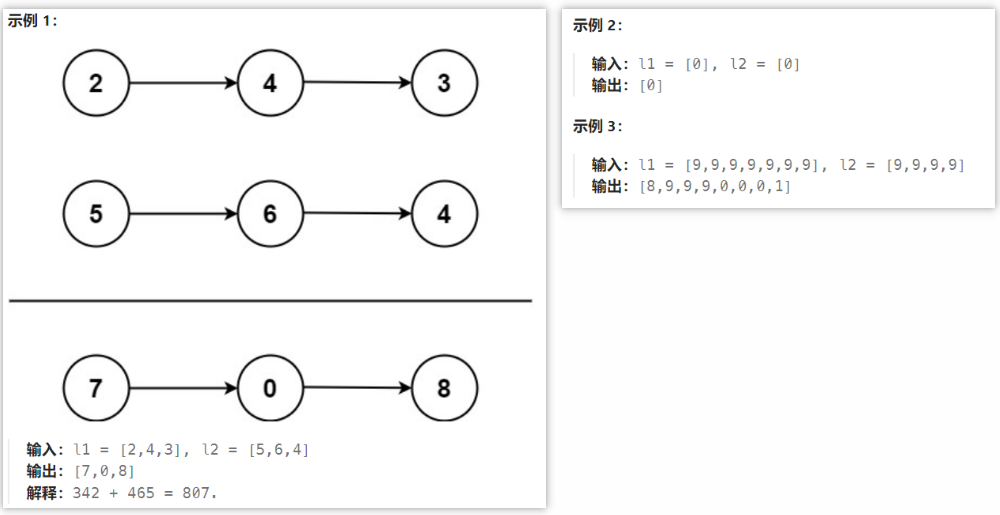
给你两个 非空 的链表,表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的,并且每个节点只能存储 一位 数字。
请你将两个数相加,并以相同形式返回一个表示和的链表。
你可以假设除了数字 0 之外,这两个数都不会以 0 开头。
2.题解思路
👻方法1:链表法
- 思路分析
- 定义虚拟链表头和对应指针,构建一个新链表用于存储相加后的结果
- 同时遍历两个链表元素,将元素相加并判断是否带进位,存储相加结果并更新进位信息,指针继续后移
/**
* 002 两数相加
*/
public class Solution1 {
/**
* 243+564=708
* 将链表元素按位对照相加,如果存在进位则放在下一个位置的相加中,直到某个链表遍历结束,最终将剩余的链表进行拼接
*/
public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
// 定义虚拟链表头
ListNode dummy = new ListNode(-1);
ListNode cur = dummy; // 定义新链表指针
// 分别定义两个待相加的链表指针
ListNode p1 = l1;
ListNode p2 = l2;
// 遍历链表,当两个链表都不为空时,按位相加
int carry = 0; // 是否存在进位
while (p1 != null || p2 != null) { // 为了不需额外处理多出来的链表,此处对于空节点的值可以置为0
int val1 = p1 == null ? 0 : p1.val;
int val2 = p2 == null ? 0 : p2.val;
int sum = val1 + val2 + carry;
// 定义新节点存储相加后的值
ListNode node = new ListNode(sum >= 10 ? (sum % 10) : sum);
cur.next = node;
cur = cur.next; // 指针指向下一位
// 更新进位信息
carry = sum / 10;
// 指针后移
if(p1!=null){
p1 = p1.next;
}
if(p2!=null){
p2 = p2.next;
}
}
// 需要将最终的进位补上(也可以将其放在上面的while条件中就不用单独拎出来)
if(carry==1){
cur.next = new ListNode(1);
}
// 返回构建的新链表
return dummy.next;
}
}
复杂度分析
时间复杂度:O(max(m,n)),其中 m 和 n 分别为两个链表的长度。我们要遍历两个链表的全部位置,而处理每个位置只需要 O(1) 的时间
空间复杂度:O(1)
🟢03-合并两个有序链表(21)
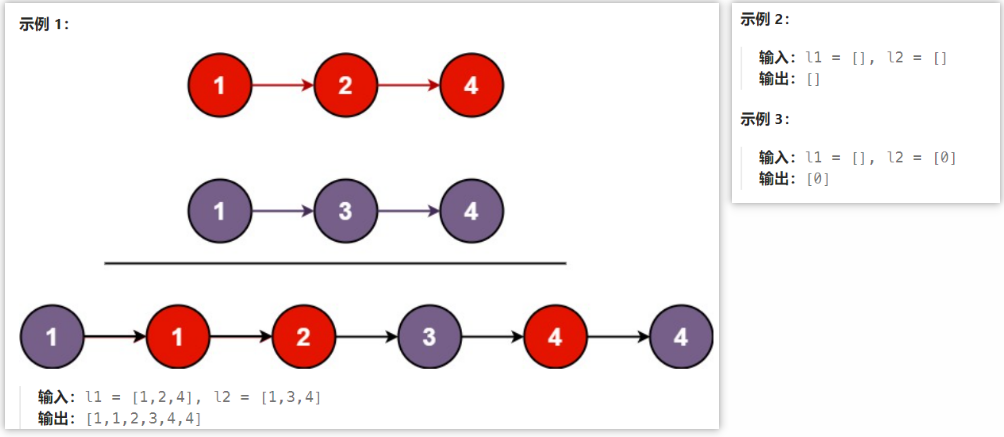
1.题目内容
将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的
2.题解思路
👻方法1:模拟比较
/**
* 021 合并两个有序链表
*/
public class Solution1 {
public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
// 定义虚拟链表头(构建新链表存储合并后的链表)
ListNode dummy = new ListNode(-1);
ListNode cur = dummy ; // 定义指针节点,指向合并后的链表
// 定义链表指针
ListNode p1 = l1;
ListNode p2 = l2;
// 遍历两个链表元素
while(p1!=null && p2!=null){
int val1 = p1.val;
int val2 = p2.val;
// 选择较小的元素优先插入
if(val1<=val2){
// 选择链表l1的当前指向元素插入
cur.next = new ListNode(val1);
p1 = p1.next; // 指针后移,指向下一个元素
cur = cur.next; // 指针后移
}else{
// 选择链表l2的当前指向元素插入
cur.next = new ListNode(val2);
p2 = p2.next; // 指针后移,指向下一个元素
cur = cur.next; // 指针后移
}
}
// 当两个链表中其中一个链表遍历到尾节点,则需将剩余节点拼接到合并后的链表尾部即可
if(p1!=null){
cur.next = p1;
}
if(p2!=null){
cur.next = p2;
}
// 返回合并后的链表
return dummy.next;
}
}
复杂度分析
时间复杂度:O(M+N)(M、N分别为两个链表的长度),合并链表需要遍历两个链表
空间复杂度:O(1) 节点引用dummy,cur 指针使用常数大小的额外空间
🟡04-随机链表的复制(138)
1.题目内容
给你一个长度为 n 的链表,每个节点包含一个额外增加的随机指针 random ,该指针可以指向链表中的任何节点或空节点。
构造这个链表的 深拷贝。 深拷贝应该正好由 n 个 全新 节点组成,其中每个新节点的值都设为其对应的原节点的值。新节点的 next 指针和 random 指针也都应指向复制链表中的新节点,并使原链表和复制链表中的这些指针能够表示相同的链表状态。复制链表中的指针都不应指向原链表中的节点 。
例如,如果原链表中有 X 和 Y 两个节点,其中 X.random --> Y 。那么在复制链表中对应的两个节点 x 和 y ,同样有 x.random --> y 。
返回复制链表的头节点。
用一个由 n 个节点组成的链表来表示输入/输出中的链表。每个节点用一个 [val, random_index] 表示:
val:一个表示Node.val的整数。random_index:随机指针指向的节点索引(范围从0到n-1);如果不指向任何节点,则为null。
你的代码 只 接受原链表的头节点 head 作为传入参数。
2.题解思路
👻方法1:哈希表(Map<oldNode,newNode>)
- 思路分析:由于random指针的存在,无法预先判断random指向的下一个节点是否已经创建过,因此采用"提前创建节点,延迟加载映射"的思路去实现
- 提前创建节点:遍历一遍原始链表,创建好新链表的节点数据(但暂时不初始化指针关系),构建原链表和新链表各个节点的映射关系(
Map<k,v> => Map<oldNode,newNode>) - 延迟加载映射:当新链表的节点构建完成,则再次遍历原始链表(或者遍历map映射关系),可根据map映射关系构建新链表的指针关系
- oldNode 与 newNode 是一一对应的,那么构建指针关系时则可通过这个map进行构建
- 提前创建节点:遍历一遍原始链表,创建好新链表的节点数据(但暂时不初始化指针关系),构建原链表和新链表各个节点的映射关系(
/**
* 138 随机链表的复制
*/
public class Solution1 {
public Node copyRandomList(Node head) {
// 定义虚拟头节点
Node dummy = new Node(-1);
Node point = dummy; // 定义新链表的指针
// 1.提前创建新节点,构建oldNode、newNode 的映射关系
Map<Node,Node> map = new HashMap<>();
Node cur = head; // 定义cur指针遍历head原始链表
while(cur!=null){
// 创建新节点
Node newNode = new Node(cur.val);
// 构建映射关系
map.put(cur,newNode);
// 遍历指针后移
cur = cur.next;
}
// 2.构建新链表的节点关系
Node pcur = head;
while(pcur!=null){
// 根据映射关系构建节点联系(设定next、random)
Node newNode = map.get(pcur);
newNode.next = map.get(pcur.next);
newNode.random = map.get(pcur.random);
// 遍历指针后移
pcur = pcur.next;
// 将新节点加入新链表
point.next = newNode;
point = point.next;
}
// 返回结果
return dummy.next;
}
}
复杂度分析
时间复杂度:O(N)遍历两轮链表(一轮创建节点,二轮更新指针)
空间复杂度:O(N)哈希表 使用线性空间大小的额外空间
🟡05-反转链表II(92)
1.题目内容
给你单链表的头指针 head 和两个整数 left 和 right ,其中 left <= right 。请你反转从位置 left 到位置 right 的链表节点,返回 反转后的链表 。

2.题解思路
理解反转链表的思路,反转链表基础版本可以通过一次遍历+头插实现,或者借助栈(先进后出)辅助操作(或者借助其他集合存储链表遍历元素,随后倒序读取构建新链表)
- 反转链表思路
- 一次遍历+头插:构建一个尾节点遍历链表元素,每次都插入元素都在链表头部,则可完成反转
- 栈/集合:借助栈或者其他集合存储链表元素,随后弹出元素(栈:先进后出)或者逆序遍历元素实现反转
/**
* 反转链表 (一整个链表反转的思路)
*/
public class Solution2 {
public ListNode reverse(ListNode head) {
// 定义虚拟链表头
ListNode dummy = null; // 此处其作为尾节点
// 定义指针用于遍历head
ListNode cur = head;
while(cur!=null){
dummy = new ListNode(cur.val,dummy); // 头插
cur = cur.next; // 指针后移
}
// 返回结果
return dummy;
}
}
/**
* 反转链表:遍历反转(结合画图理解)
*/
public class Solution1 {
public ListNode reverseList(ListNode head) {
ListNode cur = head; // 定义遍历指针
// 遍历并进行链表反转
ListNode pre = null; // 初始化
while(cur!=null){
// 反转链表
ListNode nxt = cur.next; // 记录链表的下一个节点
cur.next = pre;
// 指针往后移动等待下一轮反转
pre = cur;
cur = nxt;
}
// 返回结果
return pre;
}
}
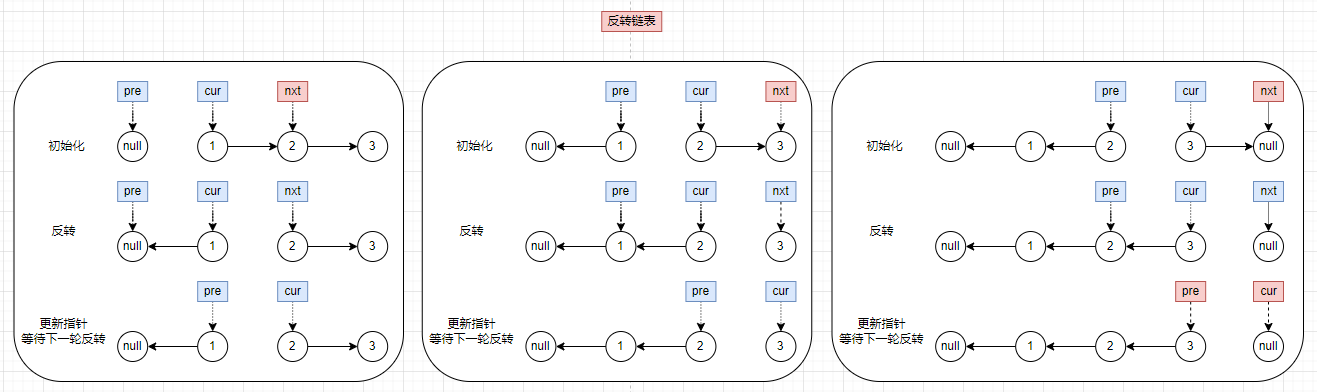
通过直接遍历反转,这个过程中需要记录3个点,一个是cur当前遍历节点(即当前要进行反转操作的节点),一个是其pre(初始化为null),一个是nxt(初始化为cur.next),反转的核心在于要让cur.next指向其前一个节点,然后让pre、cur分别往后移动,随后进行下一轮反转
当所有的元素反转完成,即操作到最后时:pre指向的就是反转的链表,而cur最终会指向null
- 记录:遍历链表元素cur,初始化是pre为null(表示尾节点),需记录
cur.next(nxt) - 反转:将cur.next指针切断指向其pre(
cur.next = pre) - 移动指针:往后移动pre、cur指针,等待下一轮反转
👻方法1:分段处理(遍历+区间反转)
此处的反转链表是限定区间的反转链表,最硬核的做法就是分段去处理,前面一段正常遍历、到了反转区间进行反转操作、剩下的链表直接拼接
/**
* 092 反转链表II
*/
public class Solution1 {
/**
* 分段处理:
* 第1段:[0,left-1] 正常遍历
* 第2段:[left,right] 反转
* 第3段:[right+1,end] 拼接
*/
public ListNode reverseBetween(ListNode head, int left, int right) {
// 定义虚拟头节点
ListNode dummy = new ListNode(-1, head); // 将head拼接过来构成一个新链表,对这个新链表进行区间反转操作:等价于ListNode dummy = new ListNode(-1); dummy.next = head;
ListNode pd = dummy; // pd指针指向新链表的头节点
/**
* 第1段:正常遍历(p、cur向前移动,到达要进行反转的左区间)
* 遍历完成 pd 的下一个节点指向的是要翻转的节点(因为dummy多了个虚拟头结点)
*/
for (int i = 0; i < left - 1; i++) {
pd = pd.next;
}
/**
* 第2段:反转这个范围区间的链表节点
*/
ListNode pre = null; // 指向前一个节点
ListNode cur = pd.next; // cur 指向当前要反转的节点(当前遍历的节点位置)
for (int i = 0; i < right - left + 1; i++) {
// 记录位置,翻转节点
ListNode nxt = cur.next; // 记录当前要翻转的下一个节点内容(避免被覆盖)
cur.next = pre; // 将cur.next指向前一个节点pre
// 更新指针位置,等待下一轮反转(pre、cur往后移动)
pre = cur;
cur = nxt;
}
// 反转完成最终cur指向的就是反转区间的下一个节点(此处也就是指代第三段区间),而pre则是指向反转完成的这个区间
// 拼接:找到第一段的拼接位置,将反转后的区间和第三段区间进行拼接(此处是先操作pd.next.next,再操作pd.next,避免影响覆盖)
pd.next.next = cur;
pd.next = pre;
return dummy.next;
}
}
复杂度分析
时间复杂度:O(n) n为链表节点个数
空间复杂度:O(1) 用到一些指针节点空间
🔴06-K个一组翻转链表(25)
1.题目内容
给你链表的头节点 head ,每 k 个节点一组进行翻转,请你返回修改后的链表。
k 是一个正整数,它的值小于或等于链表的长度。如果节点总数不是 k 的整数倍,那么请将最后剩余的节点保持原有顺序。
你不能只是单纯的改变节点内部的值,而是需要实际进行节点交换。
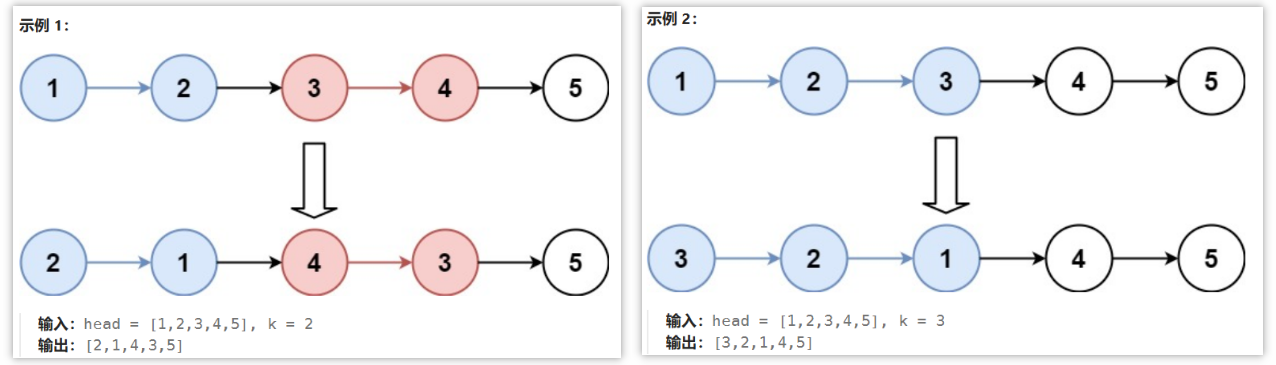
思路分析:通过模拟理解分组反转的过程,首先要进行分组反转,则需要将分组的区域圈出来,因此要先记录这个分组的前置节点pre和后置节点nxt
pre节点:对照的应该是上一组反转节点的尾节点(同理是反转之前的头节点)nxt节点:对照的应该是本组反转之前分组区域的下一个节点(因此要在每组反转之前先记录这个nxt,再断开连接进行反转)- 反转指定区域链表,反转完成随后将其拼接回去即可
pre.next=反转后的头节点、反转后的尾节点(反转前的头节点).next = nxt
2.题解思路
👻方法1:模拟法
- 思路分析:K个一组进行反转,每次找到要反转的位置节点,然后反转指定区域的链表节点,在这个过程中要记录每组反转链表区域的前后节点,用于反转后重新拼接
- ① 定义方法进行指定链表反转(传入head节点,反转链表)
- ② 遍历所有链表节点(构建虚拟头节点封装head进行遍历),定位到反转的位置,记录每一组反转区域的前置和后置节点,断开、反转后再进行拼接
- 此处先遍历一遍链表节点,将链表封装到集合中,然后通过for循环找到每个反转的位置点
- 根据这个反转位置点,找到要进行反转的头、尾节点
pre、nxt作为滚动变量记录的是每一组反转链表的前置和后置节点pre:反转后的链表的尾节点会作为下一组反转链表的前置节点(反转后更新)nxt:每次反转前要先记录当组反转链表的后置节点,反转前先断开(便于局部链表反转),反转之后再连接上
/**
* 🔴 025 K个一组反转链表
*/
class Solution {
// K 个一组反转链表
public ListNode reverseKGroup(ListNode head, int k) {
// 正序遍历链表
List<ListNode> list = new ArrayList<>();
ListNode dummy = new ListNode(-1, head);
ListNode cur = dummy;
while (cur != null) {
list.add(cur);
cur = cur.next;
}
// 遍历链表节点,K个为一组进行反转
ListNode pre = list.get(0); // 记录每一组当前反转head节点的前一个节点
ListNode nxt = null; // 记录每一组当前反转链表尾部节点的下一个节点
for (int i = 1; i < list.size(); i = i + k) {
if (i + k - 1 < list.size()) { // 不足K的剩余部分则跳过
// 截取链表节点并进行反转,反转后重新拼接
ListNode startNode = list.get(i);
ListNode endNode = list.get(i + k - 1);
// 此处需要先记录nxt,避免反转后修改
nxt = endNode.next;
endNode.next = null;
// 反转链表并拼接
pre.next = reverseLink(startNode);
startNode.next = nxt;
// 反转后的尾节点会作为下一组的反转链表的上一个节点
pre = startNode;
}
}
// 返回处理后的节点
return dummy.next;
}
// 反转指定链表
public ListNode reverseLink(ListNode node) {
if (node == null) {
return null;
}
ListNode pre = null;
ListNode cur = node;
while (cur != null) {
ListNode nxt = cur.next;
cur.next = pre;
// 滚动更新pre、cur
pre = cur;
cur = nxt;
}
// 返回反转后的链表
return pre;
}
}
复杂度分析
时间复杂度:
空间复杂度:
🟡07-删除链表的倒数第N个节点(19)
1.题目内容
给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。

2.题解思路
👻方法1:查找法
- 思路分析:核心在于找到要删除节点的前一个节点,然后调整指针
- 删除链表的节点:操作核心在于找到要删除的节点的前一个节点
prev,然后执行prev.next = prev.next.next(即将prev的下一个节点指向其下下个节点) - 如果是正向遍历删除第N个节点,则只需要遍历到
N-1的位置就可以找到这个prev - 如果是删除倒数第N个节点,则是逆向遍历的思维
- 一种思路是转正向遍历思路(即删除第
L-N+1位置的节点,但首先得直到链表节点的长度) - 一种思路是逆向遍历的思路,元素依次进栈,随后弹出N-2个元素,获取到第N-1个元素即为要删除节点的上一个节点
prev
- 一种思路是转正向遍历思路(即删除第
- 删除链表的节点:操作核心在于找到要删除的节点的前一个节点
/**
* 019 删除链表的倒数第N个节点
*/
public class Solution1 {
/**
* 核心:找到待删除节点的前一个节点
* 借助栈(先进后出)辅助存储,弹出N-2个元素,则第N-1个元素即待删除元素的前一个节点prev,调整节点指针
*/
public ListNode removeNthFromEnd(ListNode head, int n) {
// 定义虚拟头节点
ListNode dummy = new ListNode(-1, head);
ListNode cur = dummy;
// 构建栈辅助存储
Stack<ListNode> stack = new Stack<>();
// 遍历元素依次入栈
while (cur.next != null) {
stack.push(cur);
cur = cur.next;
}
// 弹出n-2个元素
for (int i = 0; i < n - 1; i++) {
stack.pop();
}
ListNode prev = stack.pop(); // 第N-1个元素即为待删除元素的上一个节点
prev.next = prev.next.next; // 删除节点
// 返回链表
return dummy.next;
}
}
复杂度分析
时间复杂度:
空间复杂度:
🟡08-删除排序链表中的重复元素II(82)
1.题目内容
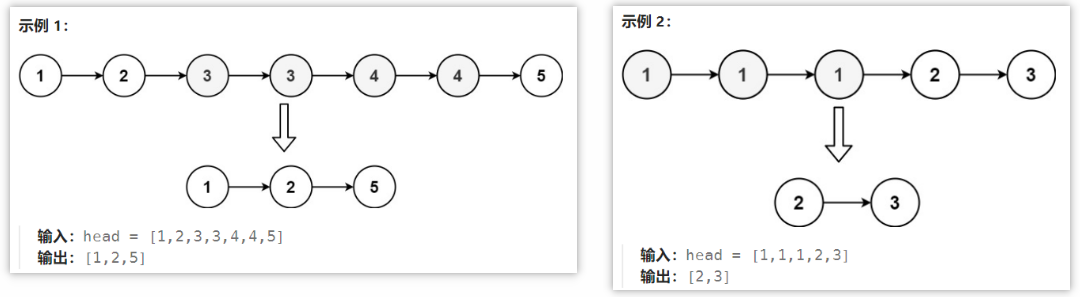
给定一个已排序的链表的头 head , 删除原始链表中所有重复数字的节点,只留下不同的数字 。返回 已排序的链表 。
2.题解思路
👻方法1:一次遍历
- 思路分析:
- 构建dummy 便于操作,借助cur 指针节点进行链表遍历
- 判断cur后两个节点是否相同(如果相同则说明出现重复元素需进行移除操作)
- 如果相同:记录当前的重复值
x,需要删除cur节点后值为x的节点(删除过程中注意空指针判断) - 如果不同:指针后移,继续遍历下一个元素
- 如果相同:记录当前的重复值
/**
* 082 删除链表中的重复元素
*/
public class Solution1 {
/**
* 思路:遍历链表元素(画图理解)
* dummy->1->1->1->2->3
* 遍历链表节点cur指向当前节点
* 1.如果当前节点的后两个节点相等则说明出现重复需执行移除操作
* 2.记录下这个重复的元素,如果cur.next.val为重复元素,则需移除cur后面这些重复的元素
*/
public ListNode deleteDuplicates(ListNode head) {
// 虚拟头节点定义,构建新链表用作遍历
ListNode dummy = new ListNode(-1);
dummy.next = head;
// 定义链表指针
ListNode cur = dummy;
// 遍历元素(判断cur后两个节点是否相同)
while(cur.next!=null && cur.next.next!=null){
// 判断cur后两个节点是否重复
if(cur.next.val == cur.next.next.val){
// 记录重复的元素,随后进行移除(即移除cur后面这些重复的元素)
int x = cur.next.val;
while(cur.next!=null && cur.next.val == x){
cur.next = cur.next.next; // 删除cur的下一个节点
}
}else{
// 不重复,指针继续后移
cur = cur.next;
}
}
// 返回链表
return dummy.next;
}
}
复杂度分析
时间复杂度:O(n)n 链表长度
空间复杂度:O(1)
🟡09-旋转链表(61)
1.题目内容
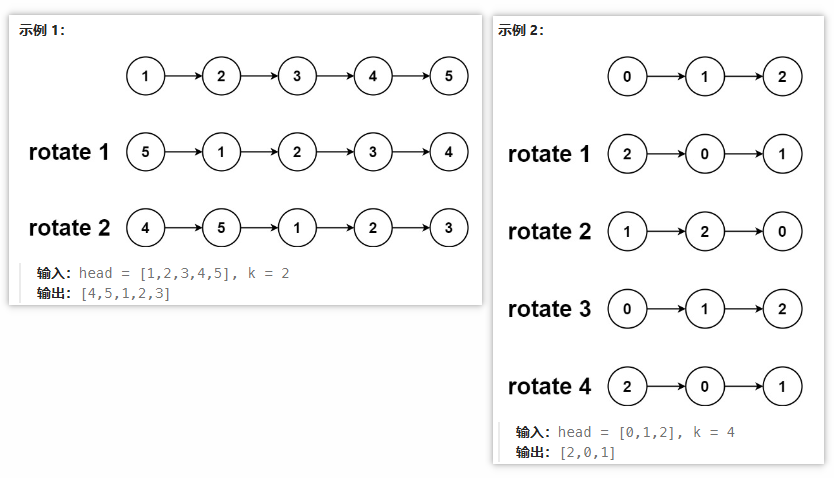
给你一个链表的头节点 head ,旋转链表,将链表每个节点向右移动 k 个位置
2.题解思路
👻方法1:三次翻转(全反转+前K反转+后N-K反转)
- 思路分析:
- 和此前的数组的元素移动概念类似,可以转化为通过多次反转实现
- 第1次反转:全链表反转
- 切割:随后遍历反转后的链表,在指定idx位置切割(获取到切割后的两个链表的头节点)
- 反转:对切割后的两个链表进行反转得到reverseA、reverseB
- 拼接:拼接反转后的链表(遍历reverseA得到其尾节点,然后让其尾节点指向reverseB)
/**
* 061 旋转链表
*/
public class Solution2 {
/**
* 思路:3次反转链表
*/
public ListNode rotateRight(ListNode head, int k) {
//边界情况
if (head == null) {
return null;
}
// 定义指针遍历链表,计算链表长度
int len = 1;
ListNode cur = head;
while (cur.next != null) { // 从1开始计数
len++;
cur = cur.next;
}
// 计算移动步数(取模得到切割点)
int idx = k % len;
if (idx == 0) {
return head; // 如果idx为0则说明不需要反转
}
// 第1次反转:整体反转
ListNode reverseAll = reverse(head);
// 获取切割的两个链表头(A、B)
ListNode p = reverseAll; // 遍历指针
for (int i = 0; i < idx - 1; i++) { // 找到切割位置
p = p.next;
}
ListNode hA = reverseAll; // A 链表头
ListNode hB = p.next; // B 链表头
p.next = null; // 断开链表
// 分别进行反转
ListNode reverseA = reverse(hA);
ListNode reverseB = reverse(hB);
// 重新拼接链表
ListNode pA = reverseA;
for (int i = 0; i < idx - 1; i++) {
pA = pA.next;
}
pA.next = reverseB; // A链表拼接B链表
// 返回拼接后的链表
return reverseA;
}
public ListNode reverse(ListNode head) {
// 反转链表节点
ListNode prev = null;
ListNode cur = head;
while (cur != null) {
ListNode nxt = cur.next; // 记录下个元素
cur.next = prev; // 反转
// 更新指针信息
prev = cur;
cur = nxt;
}
// 返回反转后的链表
return prev;
}
}
复杂度分析
时间复杂度:
空间复杂度:
👻方法2:循环链表切节点(todo)
思路分析:
- 循环一遍链表,计算链表长度N,得到真正移动(切割)的位置(
N % k) - 再遍历一遍列表,在K的位置切割(A,B),并将切割后的链表B补到A前面
- 循环一遍链表,计算链表长度N,得到真正移动(切割)的位置(
复杂度分析
时间复杂度:
空间复杂度:
🟡10-分隔链表(86)
1.题目内容
给你一个链表的头节点 head 和一个特定值 x ,请你对链表进行分隔,使得所有 小于 x 的节点都出现在 大于或等于 x 的节点之前。
你应当 保留 两个分区中每个节点的初始相对位置。

2.题解思路
👻方法1:分拆链表
- 思路分析:可以理解为分拆链表的思路
- 定义两个链表:
sml_dummy存储【节点值<x】,big_dummy存储【节点值>=x】 - 遍历链表head:依次进行比较,然后将满足条件的值添加到对应链表尾部
- 合并:遍历完成后,拼接
sml_dummy和big_dummy - 返回:最终返回拼接后的
sml_dummy.next
- 定义两个链表:
/**
* 086 分隔链表
*/
public class Solution1 {
/**
* 思路:分拆链表存储,然后合并返回
*/
public ListNode partition(ListNode head, int x) {
// 定义两个链表分别存储[val<x][val>=x]的值
ListNode smlDummy = new ListNode(-1);
ListNode bigDummy = new ListNode(-1);
// 定义链表指针
ListNode curSml = smlDummy;
ListNode curBig = bigDummy;
// 遍历元素存储数据
ListNode cur = head;
while(cur!=null){
// 根据链表节点值和x进行比较,追加到相应的链表
if(cur.val<x){
curSml.next = cur; // 追加节点到sml
curSml = curSml.next; // sml指针后移
}else{
curBig.next = cur; // 追加节点到big
curBig = curBig.next; // big指针后移
}
// 遍历指针移动
cur = cur.next;
}
// 遍历完成进行拼接
curSml.next = bigDummy.next; // 将bigDummy链表拼接到curDummy链表后面
curBig.next = null; // Error - Found cycle in the ListNode 异常处理
// 返回结果
return smlDummy.next;
}
}
复杂度分析
- 时间复杂度:O(n)遍历一遍链表
空间复杂度:O(n)需借助两个链表存储节点,节点总和为原链表节点长度
🟡11-LRU缓存(146)
1.题目内容
请你设计并实现一个满足 LRU (最近最少使用) 缓存 约束的数据结构。
实现 LRUCache 类:
LRUCache(int capacity)以 正整数 作为容量capacity初始化 LRU 缓存int get(int key)如果关键字key存在于缓存中,则返回关键字的值,否则返回-1。void put(int key, int value)如果关键字key已经存在,则变更其数据值value;如果不存在,则向缓存中插入该组key-value。如果插入操作导致关键字数量超过capacity,则应该 逐出 最久未使用的关键字。
函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。
2.题解思路
思路:哈希表和双向链表的应用,Java中提供了LinkedHashMap这种数据结构进行支持,主要是实现get、put方法:确定队头队尾(确定一端)
- LRU 淘汰策略:
- 思路1:记录元素的访问频次,每次发现超出容量阈值则淘汰访问频次最低的元素
- 思路2:借助队列,始终将经常访问的元素放在队尾,队头就是最近未被使用的元素等待下一轮淘汰

- get:访问元素
- 如果元素不存在,直接返回-1
- 如果元素存在,则需更新其位置(例如先删除后插入,让它排在后面)
- put:插入元素
- 判断操作新增是否超出阈值,如果没有则直接插入
- 如果超出阈值,则需要剔除一个最近最少使用的元素(此处可以理解为队头元素就是这个最近最少使用的缓存数据,因为get操作会将最近被访问的元素放在队尾)
👻方法1:LinkedHashMap 实现
/**
* 146 LRU缓存
*/
class LRUCache {
// 借助LinkedHashMap存储
LinkedHashMap<Integer,Integer> map ;
// 容量
int capacity ;
// 初始化
public LRUCache(int capacity) {
map = new LinkedHashMap<>();
this.capacity = capacity;
}
// get 是访问操作,如果元素存在且被访问则需更新它的位置
public int get(int key) {
if(map.containsKey(key)){
int curVal = map.get(key);
// 元素被访问,需要更新它的位置(先移除后增加)
map.remove(key);
map.put(key,curVal);
return curVal;
}else{
return -1;
}
}
public void put(int key, int value) {
// 校验元素是否存在
if(map.containsKey(key)){
// 存在则删除后再增加(确保最近访问的元素放在后面)
map.remove(key);
map.put(key,value);
}else{
// 元素不存在则校验是否超出阈值,超出阈值则需执行LRU策略腾挪位置,清理掉最近未被访问的第一个元素
if(map.size()+1>this.capacity){
// 清理最久未被使用的元素(即map的第一个元素)
map.remove(map.keySet().iterator().next());
}
// 插入新元素
map.put(key,value);
}
}
}
复杂度分析
时间复杂度:
空间复杂度:
👻方法2:手撕(双向链表+哈希表)
借助哈希表存储实际元素,双向链表维护元素访问顺序
复杂度分析
时间复杂度:
空间复杂度:
