hot150-09-二叉树系列
难度说明:🟢简单🟡中等🔴困难
hot150-09-二叉树系列
🚀二叉树遍历
基本概念补充(二叉树常用操作集合)
Queue:队列(FIFO,先进先出的有序表)- 添加元素:
add、offer - 获取元素:
remove:移出并返回目标元素peek:返回队列的第一个元素(按照入队顺序返回,但不删除元素)poll:返回队列的第一个元素(按照入队顺序返回,并删除元素)
- 添加元素:
Stack- 添加元素:
push - 获取元素:
peek:获取栈顶元素,但不删除pop:弹出栈顶元素
- 添加元素:
Deque:双端队列(Double Ended Queue),因为其既有队列又有栈的特性,因此操作方法要注意区分(建议明确First、Last方法调用,避免使用过程概念混淆)- 添加元素(区分队头、队尾操作):
- 栈的添加操作:
- 栈顶添加:
push、offFirst - 栈尾添加:
add、offer、offLast
- 栈顶添加:
- 栈的添加操作:
- 获取元素(区分队头、队尾操作):
peek:检索但不删除peek:检索但不删除此列表的头部(第一个元素)peekFirst:检索但不删除此列表的第一个元素,如果此列表为空,则返回nullpeekLast:检索但不删除此列表的最后一个元素,如果此列表为空,则返回null
poll:检索并删除poll:检索并删除此列表的头部(第一个元素)pollFirst:检索并删除此列表的第一个元素,如果此列表为空,则返回nullpollLast:检索并删除此列表的最后一个元素,如果此列表为空,则返回null
- 添加元素(区分队头、队尾操作):
🚀01-层序遍历(广度优先遍历)
(1)层序遍历-基础版
思路:借助队列辅助操作(首先要区分不同的集合选择和方法调用,避免使用过程中方法混淆导致顺序出现问题),此处如果使用Deque则应该是队列的操作
初始化队列(Queue,也可使用Deque),将根节点加入队列
当队列不为空则继续判断,其实现分析:
- 取出1个节点,然后判断它的左右节点是否存在,如果存在则将它的左右节点分别加入queue中,等待下次循环进行遍历
案例分析:
[3,9,20,null,null,15,7]- 初始化:3 进队
- 遍历,直到队列为空:
- 取出3(加入结果集),判断它存在左右节点,然后分别将
9,20加入队列,当次循环结束 - 队列不为空,继续遍历
- 取出节点9(加入结果集),判断不存在左右节点,当次循环结束
- 取出节点20(加入结果集),判断存在左右节点,将
15,7加入队列,当次循环结束 - 取出节点15(加入结果集),判断不存在左右节点,当次循环结束
- 取出节点7(加入结果集),判断不存在左右节点,当次循环结束
- 队列为空,跳出循环
- 取出3(加入结果集),判断它存在左右节点,然后分别将
- 最终返回结果集合
public List<Integer> bfs(TreeNode root){
// 定义列表存储结果集
List<Integer> res = new ArrayList<>();
// 借助队列辅助存储
Queue<TreeNode> queue = new ArrayDeque<>();
queue.offer(root); // 初始化
while(!queue.isEmpty()){
// 取出节点
TreeNode cur = queue.poll();
res.add(cur.val);
// 判断左右节点
if(cur.left!=null){
queue.offer(cur.left);
}
if(cur.right!=null){
queue.offer(cur.right);
}
}
// 返回结果集
return res;
}
(2)层序遍历-分层版
基于上述层序遍历的思路,在这个过程中将所有结果加入到结果集。如果此处希望做到分层统计的概念,则需每次进入循环遍历的时候记录当前遍历层的节点的个数n,通过这个n来达到分层统计的目的
public List<List<Integer>> bfsByLevel(TreeNode root){
// 定义列表存储结果集
List<List<Integer>> res = new ArrayList<>();
// 借助队列辅助存储
Queue<TreeNode> queue = new ArrayDeque<>();
queue.offer(root); // 初始化
while(!queue.isEmpty()){
// 获取当前队列的元素个数(用作分层统计)
int n = queue.size();
// 定义当层结果集
List<Integer> curList = new ArrayList<>();
// 分层统计
while(n>0){
// 取出节点
TreeNode cur = queue.poll();
curList.add(cur.val);
// 判断左右节点
if(cur.left!=null){
queue.offer(cur.left);
}
if(cur.right!=null){
queue.offer(cur.right);
}
n--; // 当n减为0说明当前轮次遍历结束,进入下一层
}
// 每层结果遍历完成则加入结果集,随后进入下一层遍历
res.add(curList);
}
// 返回结果集
return res;
}
🚀02-深度优先遍历(先序、中序、后序)
递归实现(DLR、LDR、LRD)
- 实现分析:
- 递归结束条件:遇到空节点就结束
- 根据先序、中序、后序的规则遍历节点
/**
* 深度优先遍历(先序DLR、中序LDR、后序LRD)
*/
public class DFSSearch {
/**
* 先序遍历:DLR
* 根节点=》左节点=》右节点
*/
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> list = new ArrayList<>();
dlr(root,list);
return list;
}
public void dlr(TreeNode root, List<Integer> list) {
if (root == null) {
return;
}
list.add(root.val);
dlr(root.left, list);
dlr(root.right, list);
}
/**
* 中序遍历:LDR
* 左节点=》根节点=》右节点
*/
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> list = new ArrayList<>();
ldr(root,list);
return list;
}
public void ldr(TreeNode root, List<Integer> list) {
if (root == null) {
return;
}
ldr(root.left, list);
list.add(root.val);
ldr(root.right, list);
}
/**
* 后续遍历:LRD
* 左节点=》右节点=》根节点
*/
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> list = new ArrayList<>();
lrd(root,list);
return list;
}
public void lrd(TreeNode root, List<Integer> list) {
if (root == null) {
return;
}
lrd(root.left, list);
lrd(root.right, list);
list.add(root.val);
}
}
非递归实现(借助栈)
递归的思路是运用了方法的调用栈,如果是非递归的方式则需要自行实现一个栈保存数据
🚀二叉树基础
🟢01-二叉树的最大深度(104)
1.题目内容
给定一个二叉树 root ,返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
2.题解思路
👻方法1:BFS(广度优先遍历)思路
- 思路分析:基于广度优先遍历思路,计算节点深度(回归【层序遍历-分层版】的思路,只不过此处只需要记录层数,不需要存储遍历结果)
/**
* 104 二叉树的最大深度
*/
public class Solution1 {
/**
* 思路:层序遍历(BFS思路),计算层数
*/
public int maxDepth(TreeNode root) {
// 空节点校验
if(root==null){
return 0;
}
// 借助队列辅助存储
Queue<TreeNode> queue = new ArrayDeque<>();
queue.offer(root); // 初始化加入根节点
// 定义变量存储下沉深度
int depth = 0;
// 遍历队列元素
while(!queue.isEmpty()){
// 分层遍历
int n = queue.size(); // 记录当前队列长度(当层遍历)
while(n>0){
// 获取当前节点
TreeNode cur = queue.poll();
// 判断是否存在左右节点
if(cur.left!=null){
queue.add(cur.left);
}
if(cur.right!=null){
queue.add(cur.right);
}
n--;
}
// 当层节点遍历完成
depth++;
}
// 返回结果
return depth;
}
}
复杂度分析
时间复杂度:O(n)需要遍历所有节点
空间复杂度:取决于队列中存储的元素数量,其在最坏情况下会达到O(n)
👻方法2:递归
- 思路分析:递归计算左右子树的深度,得到最大值
- 如果知道左子树和右子树的最大深度,那么该子树的最大深度为
max(lmax,rmax) + 1 - 因此可以递归获取到左右子树的最大深度(遍历到叶子节点结束),然后得到该子树的最大深度
- 如果知道左子树和右子树的最大深度,那么该子树的最大深度为
/**
* 104 二叉树的最大深度
*/
public class Solution2 {
/**
* 思路:递归法
* 递归计算左右子树的最大深度,直到叶子节点(叶子结点作为子树其深度为0)
*/
public int maxDepth(TreeNode root) {
if(root==null){
return 0;
}
// 分别递归计算左右子树的最大深度
int leftHeight = maxDepth(root.left);
int rightHeight = maxDepth(root.right);
// 获取到当前子树的最大深度
return Math.max(leftHeight,rightHeight) + 1;
}
}
复杂度分析
时间复杂度:
空间复杂度:
// 递归:计算二叉树的层数
private int countLevel(TreeNode root){
if(root == null){
return 0;
}
return Math.max(countLevel(root.left),countLevel(root.right)) + 1;
}
🟢02-相同的树(100)
1.题目内容
给你两棵二叉树的根节点 p 和 q ,编写一个函数来检验这两棵树是否相同。
如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的
2.题解思路
👻方法1:广度优先遍历(依次判断节点值)
/**
* 100 相同的树
*/
public class Solution3 {
/**
* 广度优先遍历
*/
public boolean isSameTree(TreeNode p, TreeNode q) {
/**
* 定义队列辅助存储(此处可以使用两个队列,也可使用同一个队列按层遍历即可)
* 每次同步存入两个元素,同步取出两个元素进行比较
*/
Queue<TreeNode> queue = new LinkedList<>(); // 此处使用LinkedList存储,允许存入null数据
queue.offer(p);
queue.offer(q);
while (!queue.isEmpty()) {
// 弹出元素进行判断(每次取出两个元素判断)
TreeNode pcur = queue.poll();
TreeNode qcur = queue.poll();
// 两个节点都为空(跳出本次循环,进行下一轮比较)
if (pcur == null && qcur == null) {
continue;
}
// 当节点不为空,校验是否匹配
if (pcur == null || qcur == null || pcur.val != qcur.val) {
return false;
}
// 插入左节点
queue.offer(pcur.left);
queue.offer(qcur.left);
// 插入右节点
queue.offer(pcur.right);
queue.offer(qcur.right);
}
return true;
}
}
复杂度分析
时间复杂度:
空间复杂度:
👻方法2:递归
public class Solution2 {
/**
* 递归思路:
*/
public boolean isSameTree(TreeNode p, TreeNode q) {
// 当p、q中存在null节点
if(p==null||q==null){
return p==q;
}
// p、q都不为null的情况下,进一步比较值,如果不匹配则直接返回false
if(p.val != q.val){
return false;
}
// 当前比较节点值匹配,继续验证其左节点、右节点
return isSameTree(p.left,q.left) && isSameTree(p.right,q.right);
}
}
复杂度分析
时间复杂度:
空间复杂度:
🟢03-翻转二叉树(226)
1.题目内容
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点
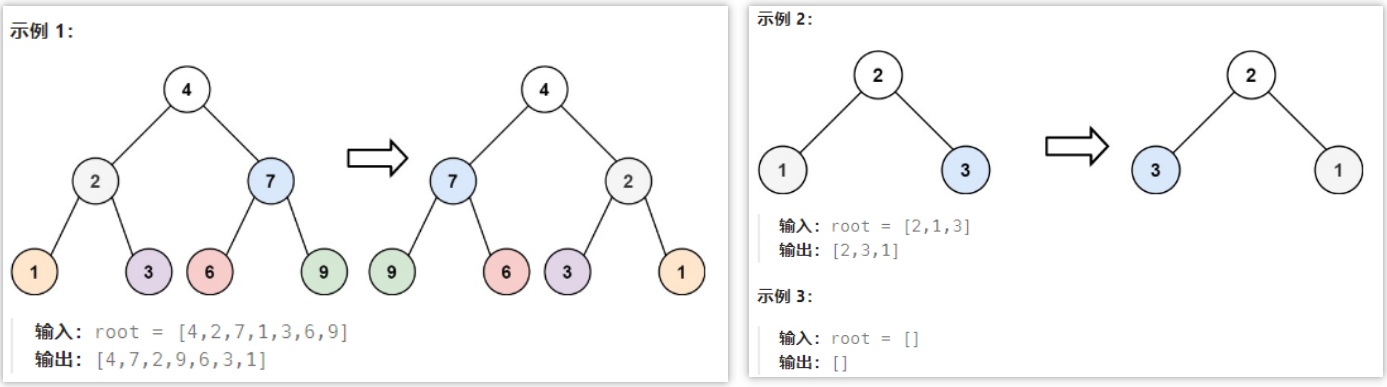
2.题解思路
👻方法1:层次遍历(边遍历边翻转)
- 思路分析:基于层次遍历的思想,每次取出一个节点遍历就交换它的左右节点即可
/**
* 226 翻转二叉树
*/
public class Solution1 {
/**
* 基于层序遍历,每遍历一个节点,交换其左右节点
*/
public TreeNode invertTree(TreeNode root) {
// root为空判断
if(root==null){
return root;
}
// 借助队列辅助
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
// 遍历队列元素(按层)
while(!queue.isEmpty()){
// 取出元素
TreeNode cur = queue.poll();
// 交换其左右节点
TreeNode temp = cur.left;
cur.left = cur.right;
cur.right = temp;
// 继续遍历
if(cur.left!=null){
queue.offer(cur.left);
}
if(cur.right!=null){
queue.offer(cur.right);
}
}
// 返回结果
return root;
}
}
复杂度分析
时间复杂度:
空间复杂度:
👻方法2:递归(思路类似DFS)
- 实现思路
- 递归出口:遇到空节点则结束
- 递归内容:非空节点则交换左右指针,并分别递归左、右节点
/**
* 226 翻转二叉树
*/
public class Solution2 {
/**
* 思路:递归
*/
public TreeNode invertTree(TreeNode root) {
if(root==null){
return root; // 节点为空,不需要执行操作
}
// 节点不为空,递归交换其左右子树
TreeNode temp = root.left;
root.left = root.right;
root.right = temp;
// 递归交换
invertTree(root.left);
invertTree(root.right);
return root;
}
}
复杂度分析
- 时间复杂度:O(N),其中 N 为二叉树节点的数目。会遍历二叉树中的每一个节点,对每个节点而言,在常数时间内交换其两棵子树
- 空间复杂度:O(N)。使用的空间由递归栈的深度决定,它等于当前节点在二叉树中的高度。在平均情况下,二叉树的高度与节点个数为对数关系,即 O(logN)。而在最坏情况下,树形成链状,空间复杂度为O(N)
🟢04-对称二叉树(101)
1.题目内容
给你一个二叉树的根节点 root , 检查它是否轴对称
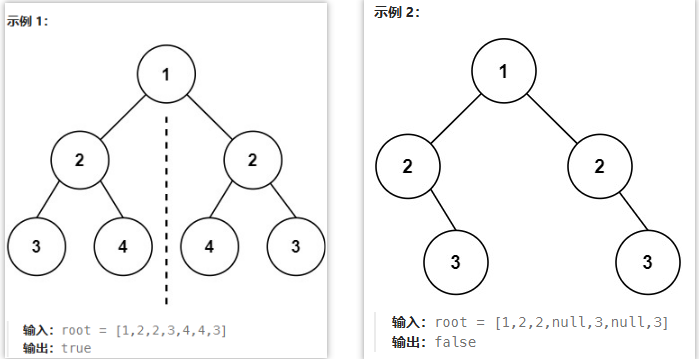
2.题解思路
👻方法1:递归思路
理解轴对称的概念:以根节点为中间轴,轴对称满足两个条件:
- 左右两个节点的val一致
- 每个树的右子树和另一个树的左子树镜像对称
采用"双指针"概念,定义两个指针分别进行游走,一开始初始化p、q都指向root,随后分别向相反方向遍历,检查任意时刻p、q指针指向的节点值是否相等,如果相等则继续遍历其左右子树是否对称
public boolean isSymmetric(TreeNode root) {
// p、q的起始节点均从root开始
return check(root,root);
}
public boolean check(TreeNode p, TreeNode q) {
// 边界条件检验
/* 如果p、q都为null */
if (p == null && q == null) {
return true;
}
/* 如果p、q两者中有一个为null,明显不符合镜像对称要求 */
if (p == null || q == null) {
return false;
}
/* p、q都不为null,需校验指针对应的节点值,及其子树的值(子树对称可通过递归校验) */
// if (p != null && q != null) {}
return p.val==q.val && check(p.left, q.right) && check(p.right, q.left);
}
复杂度分析
时间复杂度:遍历了这棵树,渐进时间复杂度为 O(n)
空间复杂度:空间复杂度和递归使用的栈空间有关,这里递归层数不超过 n,故渐进空间复杂度为 O(n)
👻方法2:层序遍历
- 思路分析:和相同的树这道题目的层序遍历类似,其实现思路是将要比较的元素两两放入到队列中,然后每次取出两个进行比较。类似的,基于本题对称二叉树的设定,也是通过层序遍历的方式和将节点放入队列,然后两两取出进行比较。但此处需注意的是此时两两放入的元素应该是左右对称放入进行比较(而非校验相同的树中左左、右右进行比较)
/**
* 101 对称二叉树
*/
public class Solution2 {
/**
* 转换题意:相同的树(仿照思路)
* 判断左右子树是否对称(左右节点比较)
*/
public boolean isSymmetric(TreeNode root) {
return check(root, root);
}
/**
* 基于层次遍历判断两个树是否对称
*/
public boolean check(TreeNode p, TreeNode q) {
// 借助队列辅助存储
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(p);
queue.offer(q);
while(!queue.isEmpty()){
// 两两比较
TreeNode curP = queue.poll();
TreeNode curQ = queue.poll();
// 如果两个节点都为空,则无需比较,跳过本轮
if(curP==null && curQ==null){
continue;
}
// 如果其中一个为空,则不对称
if(curP==null || curQ==null){
return false;
}
// 如果两个都不为空,则进一步校验值
if(curP.val != curQ.val){
return false;
}
// 将左、右节点加入队列,进行下一步判断
queue.add(curP.left);
queue.add(curQ.right);
queue.add(curP.right);
queue.add(curQ.left);
}
return true;
}
}
复杂度分析
时间复杂度:O(n)
空间复杂度:O(n) 需要一个队列维护节点(每个节点最多进队一次、出队一次),队列中不会超过n个节点,渐进空间复杂度为O(n)
🟡04-从前序和中序遍历序列构造二叉树(105)
1.题目内容
思路核心
思路核心:画图、递归构建左右子树、基于前序序列构造(前序确定根节点),中序序列打辅助(中序确定左右子树节点个数,即长度)
- 画图,勾勒出数组的左右区间等关系
- 构建子树:递归构建,基于前序序列构建
- 判断递归出口:前序序列的左右指针相遇则返回null
- 确定递归的左右区间边界(结合中序序列来辅助),确定区间的下标索引
- 随后依次创建根节点、递归构建左子树、右子树
- 最终返回创建好的节点
2.题解思路
👻方法1:递归法(画图+构建)
复杂度分析
时间复杂度:
空间复杂度:
【步骤1】:梳理序列的对照关系(根节点元素及位置,对应左右子树在各个序列的边界)
中序遍历(left->root->right):【【左子树的inOrder结果】,根节点,【右子树的inOrder结果】】
前序遍历(root->left->right):【根节点,【左子树的preOrder结果】,【右子树的preOrder结果】】
(1)根节点的确认:根据前序遍历的第一个元素确定根节点值,然后根据val在中序遍历中定位根节点的位置(索引)
(2)判断左右节点的个数(实际为定位根节点在中序序列的位置):确定了根节点的位置后,在中序遍历中根节点左边就是左子树的节点个数、根节点右边就是右子树的节点个数
(3)左右子树的构建:结合图示理解分析(通过划分数组的下限,定义不同的下标/游标实现编码),前序遍历的左右游标(preLeft、preRight),中序遍历的左右游标(inLeft、inRight)

数据的对应关系可以拆解为:(梳理每个序列的根节点位置,和对应左右子树的边界索引,确定两个序列的对照关系(即对应子树的元素))
以中序遍历为参考,其左侧是左子树的所有节点,这些节点在前序遍历中对应的位置是根据根节点下一个位置+子节点个数进行确定的
- 即中序遍历
[inLeft,pivot-1](左子树)对应前序遍历中[preLeft+1,preLeft+左子树节点个数],而左子树节点个数在中序遍历中可以通过pivot-inLeft得到 - 基于此分析左子树的关系映射为:中序的
[inLeft,pivot-1]元素 =[preLeft+1,preLeft+pivot-inLeft]元素
- 即中序遍历
同理继续基于此梳理右子树的游标关系:中序的
[pivot+1,inRight]元素=[preLeft+pivot-inLeft+1,preRight]元素
【步骤2】创建根节点并递归构建左右子树
左右子树的构建最终是落实到子节点的创建,因此基于上述关系分析,可进一步构造递归函数进行构建(首先就是确定递归函数的入参和出参),递归的结束条件就是边界相遇,基于前序遍历序列去构建,借助中序遍历序列确定子树节点个数
- (1)确定递归退出条件(基于前序遍历序列构建,当前序的两个边界相遇则退出,即
preLeft>preRight时return) - (2)正常创建根节点(递归的最终也是落实到单个节点的创建)并设置其相应的左右子树
- 此处结合图示进行理解,按照图示参数一步步拿到需要的值并设置
/**
* 105.从前序和中序遍历序列中构造二叉树
*/
public class Solution1 {
public TreeNode buildTree(int[] preorder, int[] inorder) {
TreeNode root = buildTreeHelper(preorder,inorder,0,preorder.length-1,0,inorder.length-1);
return root;
}
// 前序遍历序列、中序遍历序列、子树的前序左右边界(preLeft、preRight)、子树的中序左右边界(inLeft、inRight)
public TreeNode buildTreeHelper(int[] preorder, int[] inorder,int preLeft,int preRight,int inLeft,int inRight) {
// 基于前序遍历序列去构建,借助中序遍历序列确定左子树节点个数,如果左右边界相遇则结束
if(preLeft>preRight){
return null;
}
// 满足条件则递归构建子树(最终落实到创建节点)
// 1.确定根节点(前序序列的第一个元素)
TreeNode root = new TreeNode(preorder[preLeft]);
// 2.计算左子树的元素长度(leftCount = pivot-inLeft),其中pivot为根节点在中序遍历序列的下标索引(自定义工具方法获取)
// int leftCount = getRootIndex(root.val,inorder) - inLeft ;
int pivot = getRootIndex(root.val,inorder) ; // 如果此处对照图示则an按照图示的参数定义便于理解,避免混淆
// 3.递归构建左右子树(结合图示设置值即可)
root.left = buildTreeHelper(preorder,inorder,preLeft+1,preLeft+pivot-inLeft,inLeft,pivot-1);// 对应传入左子树的前序左右边界和中序左右边界
root.right = buildTreeHelper(preorder,inorder,preLeft+pivot-inLeft+1,preRight,pivot+1,inRight);// 对应传入右子树的前序左右边界和中序左右边界
// 返回创建的节点信息
return root;
}
/**
* 根据val值获取其在对应数组的下标位置
* @param val
* @return
*/
private int getRootIndex(int val,int[] inorder){
for(int i=0;i<inorder.length;i++){
if(inorder[i]==val){
return i;
}
}
return -1;
}
}
基于上述优化方向,会从getRootIndex这个定位根节点位置的方法进行切入,先将inorder数组转为哈希表存储(map),提升数据快速检索定位效率,需注意的是,此处存储的是非重复元素
- 复杂度分析
- 时间复杂度:O(n),其中 n 是树中的节点个数
- 空间复杂度:O(n),除去返回的答案需要的 O(n) 空间之外,还需要使用 O(n) 的空间存储哈希映射,以及 O(h)(其中 h 是树的高度)的空间表示递归时栈空间。这里 h<n,所以总空间复杂度为 O(n)
🟡05-从中序和后序遍历序列构造二叉树(106)
1.题目内容
基于中序和后续序列构造二叉树,其思路和前序+中序的方式类似,确定好每次的边界条件
2.题解思路
- 和从中序和前序序列构造二叉树的解决方案类似,只不过此处注意LRD序列的root是最后一个元素,其次要注意边界的问题
- 计算一个区间的长度公式:
终点-起点+1=size - 如果无法明确一个区间终点位置,则采用方程式的形式来进行处理

/**
* 106 从后序遍历和中序遍历序列构造二叉树
*/
public class Solution1 {
/**
* 基于后序序列构建(得到root),中序序列辅助(计算长度)
*/
public TreeNode buildTree(int[] inorder, int[] postorder) {
return buildTreeHelper(inorder, postorder, 0, inorder.length - 1, 0, postorder.length - 1);
}
public TreeNode buildTreeHelper(int[] inorder, int[] postorder, int inL, int inR, int postL, int postR) {
// 基于后序序列构建,当两个指针相遇则为递归出口
if (postL > postR) {
return null;
}
// 根据root节点获取其在inorder下的索引位置,以确定左右子树的节点个数
int idx = getRootIndex(postorder[postR], inorder);
int leftSize = idx - inL;
// 构建节点:root、left、right
TreeNode root = new TreeNode(postorder[postR]);
root.left = buildTreeHelper(inorder, postorder, inL, idx - 1, postL, postL + leftSize - 1);
root.right = buildTreeHelper(inorder, postorder, idx + 1, inR, postL + leftSize, postR - 1);
// 返回构建的节点
return root;
}
public int getRootIndex(int target, int[] inorder) {
for (int i = 0; i < inorder.length; i++) {
if (inorder[i] == target) {
return i;
}
}
return -1;
}
}
🟡06-填充每个节点的下一个右侧节点指针II(117)
1.题目内容
给定一个二叉树:
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL 。
初始状态下,所有 next 指针都被设置为 NULL 。
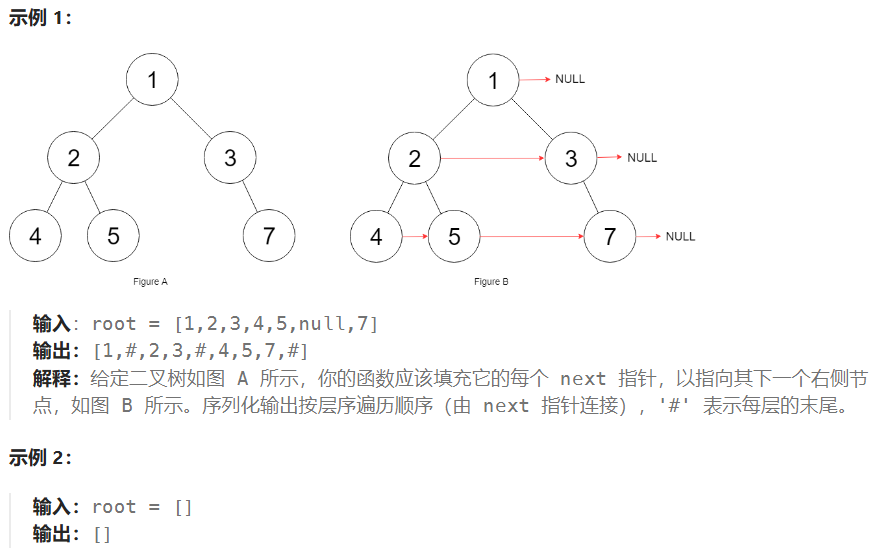
2.题解思路
👻方法1:层次遍历(从上到下按层,从右到左遍历)
- 思路分析:基于层次遍历的思路,只不过此处是采用从上到下,从右到左的方向进行遍历,基于此当按层遍历的时候可以定义一个tempNode始终存放上一个遍历节点(这个节点会作为下一个遍历节点的next)
/**
* 117 填充每个节点的下一个右侧节点指针II
*/
public class Solution2 {
/**
* 基于层序遍历的思路实现
* root、right、left(从上到下,从右到左的方向进行遍历)
*/
public Node connect(Node root) {
// null判断
if (root == null) {
return root;
}
// 定义辅助队列存储遍历节点
Deque<Node> queue = new LinkedList<>();
queue.add(root); // 初始化队列
// 层序遍历(从上到下,从右到左)
while (!queue.isEmpty()) {
int size = queue.size(); // 获取当前队列size(当层节点个数)
Node tempNextNode = null; // 定义临时节点存储这个next
for (int i = 0; i < size; i++) {
// 遍历当层元素
Node cur = queue.poll();
// 将右、左节点分别先后加入队列
if (cur.right != null) {
queue.add(cur.right); // 此处添加的是cur.right(不要犯常识性错误)
}
if (cur.left != null) {
queue.add(cur.left);
}
/**
* 构建cur的指针关系(cur指向的是右边的节点)
* 如果入队是先右后左的话,那么上一个入队的元素会作为下一个节点的next
*/
cur.next = tempNextNode; // 上一个入队的元素会作为下一个节点的next(当前cur.next指向的就是上一个遍历节点)
tempNextNode = cur; // 更新cur为tempNextNode,其会作为下一个遍历节点的next
}
}
return root;
}
}
/**
* Node 节点定义
*/
class Node {
int val;
Node left; // 左节点
Node right; // 右节点
Node next; // next指针
Node(int val){
this.val = val;
}
}
复杂度分析
时间复杂度:O(N) N 为树中所有节点个数
空间复杂度:O(N)队列的空间代价
🟡07-二叉树展开为链表(114)
1.题目内容
给你二叉树的根结点 root ,请你将它展开为一个单链表:
- 展开后的单链表应该同样使用
TreeNode,其中right子指针指向链表中下一个结点,而左子指针始终为null - 展开后的单链表应该与二叉树 先序遍历 顺序相同
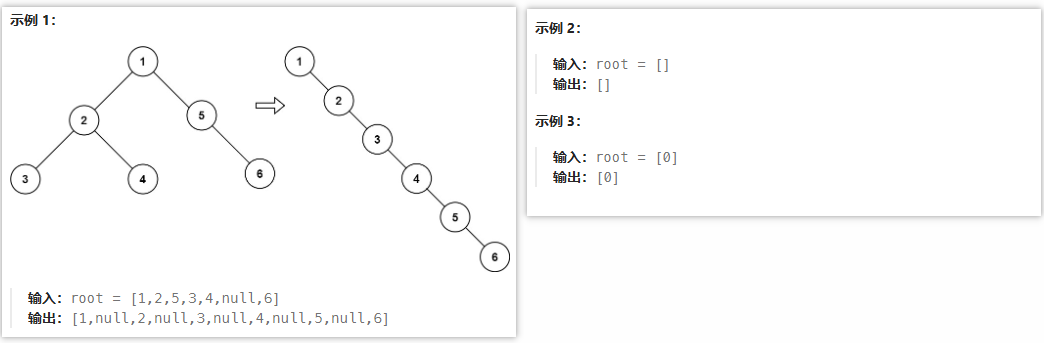
2.题解思路
👻方法1:遍历+移动
- 思路分析:遍历每个节点,如果存在左子树则移动(原左移右,现左置空,原右移到现右(原左)的最右侧),单个节点遍历/移动完成则指针继续向右移动
- 遍历
root树,定义cur指针指向遍历节点 - 当
cur不为叶子节点时则进入循环判断是否需要进行移动- 如果
cur.left不为空,则需执行移动操作(移动前需要记录原来的左右子树)- 左子树的处理:将
cur.left移动到cur的右侧,并将cur左侧置为空 - 右子树的处理:需要找到移动后的
左子树的最右侧的节点,然后将cur.right放在这个最右节点的右侧
- 左子树的处理:将
- 移动完成,此时可以指向下一个节点进行遍历
cur = cur.right(因为左节点被搬到右边了,因此指针始终指向右边的节点,然后依次进行遍历)
- 如果
- 遍历
/**
* 114 二叉树展开为链表
*/
public class Solution1 {
/**
* 遍历的思路:
* 1.定义cur指针进行遍历
* 2.如果节点存在则判断其是否存在左子树需要移动
* - 如果存在左子树,则进行移动操作:a.将左子树移动到右侧 b.原左子树位置置空 c.将其原右子树的位置拼接到移动后的左子树的最右侧节点
* - 如果节点不存在左子树,则不需要执行任何操作
* 3.本次遍历操作完成,继续下一次遍历(cur始终指向右侧节点,因为在这个过程中,左侧子树会被移动到右侧)
*/
public void flatten(TreeNode root) {
// 1.定义cur指针,指向当前遍历节点
TreeNode cur = root;
// 当节点不为叶子节点,则依次判断是否需要进行移动
while (cur != null) {
// 记录cur原来的左右子树(节点)
TreeNode leftTree = cur.left;
TreeNode rightTree = cur.right;
// 如果左子树不为空,则需要将其搬到右侧
if (leftTree != null) {
// a.左子树处理
cur.right = leftTree; // 将左子树搬到右侧
cur.left = null; // 原来左子树的位置置空
// b.右子树处理(找到移动后的leftTree的左右侧节点,然后将原rightTree放到其右侧)
TreeNode findRightNode = leftTree; // 定义指针遍历寻找原左子树的最右侧节点
while (findRightNode.right != null) { // 当右侧节点不为空则一直向下找,直到找到最右侧节点
findRightNode = findRightNode.right;
}
// 找到这个最右侧节点(叶子节点),然后将原来的rightTree放置在其右侧
findRightNode.right = rightTree;
}
// 如果左子树为空,则不需要做任何操作,继续遍历下一个右侧节点
cur = cur.right;
}
}
}
复杂度分析
时间复杂度:
空间复杂度:
🟢08-路径总和(112)
1.题目内容
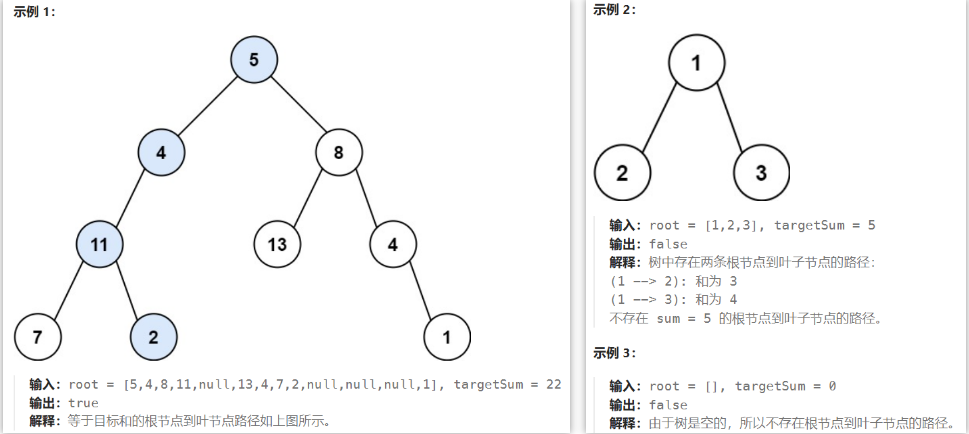
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 true ;否则,返回 false 。
叶子节点 是指没有子节点的节点。
2.题解思路
👻方法1:广度优先遍历(🚀)
结合题意分析,从根节点到叶子节点的路径中节点之和等于targetSum。回归最原始的思路就是遍历到每个叶子节点,然后计算其路径和。可以基于广度优先搜索的方式,借助两个队列进行存储:
- 节点队列:存储每个遍历的节点(基于BFS存取)
- 路径和队列:存储从根结点到每个遍历的节点的路径和(避免重复计算)
- 遍历节点的过程中判断是否为叶子节点,如果是叶子结点则进一步判断当前路径和是否满足targetSum(满足则直接返回true),不满足则继续遍历
/**
* 112 路径之和
*/
public class Solution1 {
/**
* 基于广度优先遍历的思路:BFS 借助队列存取
* - 节点队列:存储每个遍历的节点
* - 路径和队列:存储root到每个遍历的节点的路径和
* 遍历的过程中判断root到leaf的节点是否满足targetSum
*/
public boolean hasPathSum(TreeNode root, int targetSum) {
// 空节点判断
if (root == null) {
return false;
}
// 构建队列存储
Deque<TreeNode> nodeQueue = new LinkedList<>();
nodeQueue.offer(root);
Deque<Integer> valQueue = new LinkedList<>();
valQueue.offer(root.val);
while (!nodeQueue.isEmpty()) {
// 取出节点,然后按层次遍历
TreeNode node = nodeQueue.poll();
int cur = valQueue.poll();
// 判断是否为叶子节点以及路径和是否满足要求
if (node.left == null && node.right == null) {
// 如果为叶子节点(左右节点为null),则进一步判断是否存在满足条件的target
if (cur == targetSum) {
return true;
}
}
// 非叶子结点则继续判断并加入队列
if (node.left != null) {
nodeQueue.offer(node.left);
valQueue.offer(cur + node.left.val);
}
if (node.right != null) {
nodeQueue.offer(node.right);
valQueue.offer(cur + node.right.val);
}
}
return false;
}
}
复杂度分析
时间复杂度:O(N) N 是树的节点数(对每个节点访问一次)
空间复杂度:O(N)空间复杂度主要取决于队列的开销(队列中的元素个数不会超出 N )
👻方法2:递归
- 思路分析:将题意转化为是否存在从当前节点 root 到叶子节点的路径,满足其路径和为sum。假设从根结点到当前节点的值之和为
val,将大问题转化为小问题(是否存在从当前节点的子节点到叶子结点的路径满足其路径和为sum-val)
/**
* 112 路径之和
*/
public class Solution2 {
/**
* 递归
*/
public boolean hasPathSum(TreeNode root, int targetSum) {
// 递归出口
if (root == null) {
return false;
}
// 叶子节点判断
if (root.left == null && root.right == null) {
return root.val == targetSum;
}
// 递归判断
return hasPathSum(root.left, targetSum - root.val) || hasPathSum(root.right, targetSum - root.val);
}
}
复杂度分析
时间复杂度:O(N) N 是树的节点数(对每个节点访问一次)
空间复杂度:O(H)H 是树的高度(空间复杂度主要取决于递归时栈空间的开销,最坏情况下树呈链状(O(N),平均情况下树的高度和节点对数正相关O(log N)))
👻方法3:DFS
- 思路分析
- 使用全局变量res记录结果,递归过程中每次使用目标值减去当前节点的值,当遍历到子节点的时候,如果子节点的val与剩余的targetSum相等则说明能找到一条路径,且这条路径上的总和和targetSum相等
/**
* 112 路径之和
*/
public class Solution3 {
boolean res = false; // 定义全局变量存储结果
/**
* 递归
*/
public boolean hasPathSum(TreeNode root, int targetSum) {
// root 为空
if (root == null) {
return false;
}
dfs(root, targetSum);
return res;
}
/**
* 深度优先遍历
*/
public void dfs(TreeNode root, int targetSum) {
// 递归出口
if (root == null) {
return;
}
if (root.left == null && root.right == null && root.val == targetSum) {
res = true;
}
dfs(root.left, targetSum - root.val);
dfs(root.right, targetSum - root.val);
}
}
复杂度分析
时间复杂度:O(N) N 是树的节点数(对每个节点访问一次)
空间复杂度:O(H)H 是树的高度(空间复杂度主要取决于递归时栈空间的开销,最坏情况下树呈链状(O(N),平均情况下树的高度和节点对数正相关O(log N)))
🟡09-求根节点到叶节点数字之和(129)
1.题目内容
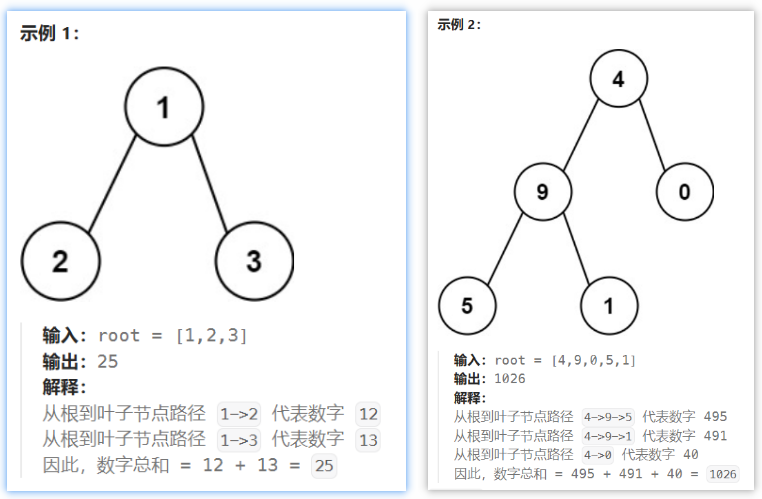
给你一个二叉树的根节点 root ,树中每个节点都存放有一个 0 到 9 之间的数字。
每条从根节点到叶节点的路径都代表一个数字:
- 例如,从根节点到叶节点的路径
1 -> 2 -> 3表示数字123。
计算从根节点到叶节点生成的 所有数字之和 。
叶节点 是指没有子节点的节点。
2.题解思路
👻方法1:层序遍历(🚀)
- 思路分析:基于层序遍历思路,参考==路径总和(112)==的BFS思路,通过维护两个队列(存储遍历节点,root到当前节点的路径和(数字拼接)),在遍历的过程中判断是否为叶子节点,如果为叶子节点则计算当前累加和,如果非叶子节点则继续拼接路径并存储
/**
* 求根节点到叶节点数字之和(129)
*/
public class Solution1 {
public int sumNumbers(TreeNode root) {
if (root == null) {
return 0;
}
Deque<TreeNode> queue = new LinkedList<>();
queue.offer(root);
Deque<Integer> valQueue = new LinkedList<>();
valQueue.offer(root.val);
int res = 0;
while (!queue.isEmpty()) {
int size = queue.size();
for (int i = 0; i < size; i++) {
TreeNode curNode = queue.poll();
int val = valQueue.poll();
// 判断是否为叶子节点,如果为叶子节点则将当前路径和进行累加
if (curNode.left == null && curNode.right == null) {
res = res + val;
}
// 将节点和对应路径值加入队列
if (curNode.left != null) {
queue.offer(curNode.left);
valQueue.offer(val * 10 + curNode.left.val); // 将拼接的数字放入
}
if (curNode.right != null) {
queue.offer(curNode.right);
valQueue.offer(val * 10 + curNode.right.val); // 将拼接的数字放入
}
}
}
// 返回结果
return res;
}
}
复杂度分析
时间复杂度:O(N) N为树节点个数
空间复杂度:O(N)空间占用取决于队列
🔴10-二叉树中的最大路径和(124)
1.题目内容
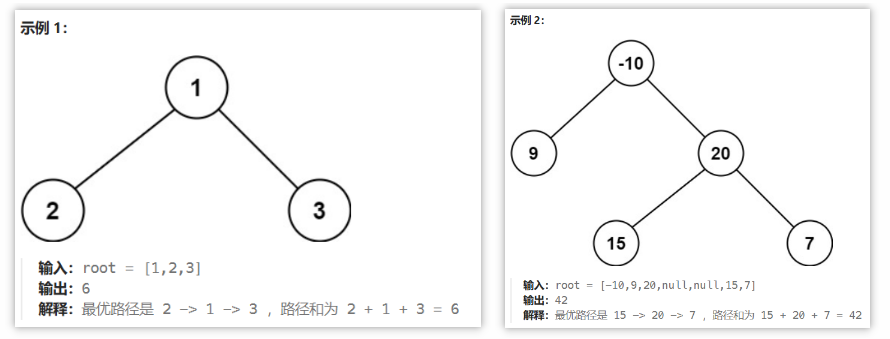
二叉树中的 路径 被定义为一条节点序列,序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点,且不一定经过根节点
路径和 是路径中各节点值的总和
给你一个二叉树的根节点 root ,返回其 最大路径和
2.题解思路
👻方法1:👻方法1:结合543-二叉树的最长直径进行分析
/**
* 🔴 124 二叉树中的最大路径和
*/
public class Solution1 {
public int maxSum = Integer.MIN_VALUE;
public int maxPathSum(TreeNode root) {
// 调用递归方法
dfs(root);
// 返回结果
return maxSum;
}
// 递归处理(dfs返回的是链的节点值之和,而不是直径的节点值之和)
private int dfs(TreeNode node) {
if (node == null) {
return 0; // 没有节点,和为0
}
// 计算左子树的最大链和
int L = dfs(node.left);
// 计算右子树的最大链和
int R = dfs(node.right);
// 两条链拼成路径
maxSum = Math.max(maxSum, L + R + node.val);
// 返回当前子树最大链和,向上层调用返回(如果必须选当前节点)的一定是当前节点+max(左树,右树),不然上一级就无法连城一条线了
return Math.max(Math.max(L, R) + node.val, 0);
}
}
复杂度分析
时间复杂度:O(n),其中 n 为二叉树的节点个数
空间复杂度:O(n)。最坏情况下,二叉树退化成一条链,递归需要 O(n) 的栈空间
🟡11-二叉搜索树迭代器(173)
1.题目内容
实现一个二叉搜索树迭代器类BSTIterator ,表示一个按中序遍历二叉搜索树(BST)的迭代器:
BSTIterator(TreeNode root)初始化BSTIterator类的一个对象。BST 的根节点root会作为构造函数的一部分给出。指针应初始化为一个不存在于 BST 中的数字,且该数字小于 BST 中的任何元素。boolean hasNext()如果向指针右侧遍历存在数字,则返回true;否则返回false。int next()将指针向右移动,然后返回指针处的数字。
注意,指针初始化为一个不存在于 BST 中的数字,所以对 next() 的首次调用将返回 BST 中的最小元素。
你可以假设 next() 调用总是有效的,也就是说,当调用 next() 时,BST 的中序遍历中至少存在一个下一个数字。

2.题解思路
👻方法1:扁平化(转LDR的list进行迭代)
- 思路分析:将二叉树转化为
LDR中序遍历的结果列表(数组)存储,然后可以用得到的数组本身来实现迭代器的效果LDR:定义列表存储LDR遍历结果,point定义迭代指针索引(初始化:0)hasNext():如果指针指向数组之外说明没有下一个值next():根据当前point获取值,然后point++继续指向下一个可迭代的索引位置
/**
* 173 二叉搜索树迭代器
*/
class BSTIterator {
List<Integer> list ;// 存储LDR中序遍历结果
int point ; // 指针
public BSTIterator(TreeNode root) {
list = new ArrayList<>();
point = 0; // 需初始化为一个不存在于bst中的数字,且该数字小于bst中任何元素
ldr(root,list);
}
/**
* 中序遍历
*/
public void ldr(TreeNode root,List<Integer> list) {
if (root == null) {
return;
}
// LDR:left->ROOT->RIGHT
ldr(root.left,list);
list.add(root.val);
ldr(root.right,list);
}
public int next() {
if(point<list.size()){
return list.get(point++); // 返回值,然后 point 指向指针移动
}else{
return -1; // 不存在
}
}
public boolean hasNext() {
return point<list.size(); // point超出listSize说明不存在next
}
}
复杂度分析
时间复杂度:O(N) N 为树节点
空间复杂度:O(N)空间复杂度为辅助列表存储需要占用的空间
👻方法2:迭代(LDR+栈)
- 思路分析:
LDR+ 栈(不提前获取LDR序列,而是实时维护stack信息)- 栈
stack:用于存储当前待遍历的节点,cur指向当前指针位置 next():- 当节点不为空,则不断遍历其左子树并将节点入栈(左节点)
- 当节点为空时,弹出栈顶元素(元素弹出表示已遍历过)
- 栈
/**
* 173 二叉搜索树迭代器
*/
class BSTIterator {
Stack<TreeNode> stack; // 栈存储待遍历的元素
TreeNode cur;// 指向当前节点
public BSTIterator(TreeNode root) {
stack = new Stack<>();
cur = root; // 指针初始化
}
public int next() {
// 当cur不为空,一直遍历左子树(直到cur为null退出)
while (cur != null) {
stack.push(cur);
cur = cur.left;
}
// 节点为空则弹出栈顶元素
cur = stack.pop();
int val = cur.val;
// 遍历右节点
cur = cur.right;
return val;
}
public boolean hasNext() {
// 当指针节点为null且栈为空表示遍历完毕
return cur != null || !stack.isEmpty();
}
}
复杂度分析
时间复杂度:初始化和hasNext方法调用需要O(1)时间,但对于next方法最坏情况下需要O(n)的时间
空间复杂度:O(n)空间复杂度取决于栈深度(极端情况下当二叉树为一条链的情况下会到达O(n)的级别)
🟢12-完全二叉树的节点个数(222)
1.题目内容
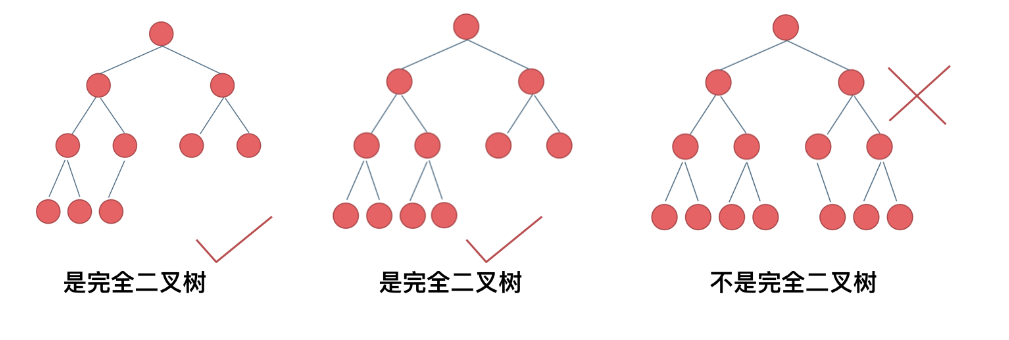
给你一棵 完全二叉树 的根节点 root ,求出该树的节点个数。
完全二叉树 的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层,则该层包含 1~ 2h 个节点。
2.题解思路
👻方法1:针对完全二叉树的解法(判断子树是否为满二叉树,分情况讨论)
思路分析:结合完全二叉树的特点进行计算
- 通过比较两棵子树的高度来进行计算,如果子树是满二叉树则借助公式进行计算,如果子树非满二叉树则采用递归方式计算
public class Solution3 { /** * 针对完全二叉树的解法: * 深度 */ public int countNodes(TreeNode root) { // root 为null判断 if (root == null) { return 0; } // 判断子树是否为满二叉树,如果不是则递归计算 int leftDepth = 0, rightDepth = 0; // 计算左子树的深度 TreeNode curLeft = root.left; while (curLeft != null) { leftDepth++; curLeft = curLeft.left; } // 计算右子树的深度 TreeNode curRight = root.right; while (curRight != null) { rightDepth++; curRight = curRight.right; } // 判断左右子树的深度是否相同(如果递归向左向右深度相同则说明是满二叉树,则借助公式计算) if (leftDepth == rightDepth) { return (2 << leftDepth) - 1; // 注意(2<<1) 相当于2^2,所以leftDepth初始为0 } // 如果左右子树深度不同,即非满二叉树则继续递归计算 return countNodes(root.left) + countNodes(root.right) + 1; } }复杂度分析
时间复杂度:
空间复杂度:
👻方法2:层序遍历(BFS)❌ 迭代法
- 思路分析:中规中矩进行层序遍历
/**
* 222 完全二叉树的节点个数
*/
public class Solution1 {
/**
* 层序遍历
*/
public int countNodes(TreeNode root) {
// root 为null判断
if(root==null){
return 0;
}
Deque<TreeNode> queue = new LinkedList<>();// 辅助队列
queue.offer(root); // 初始化
int count = 0;// 定义计数器
while(!queue.isEmpty()){
TreeNode cur = queue.poll();
// 节点计数
count++;
// 加入左、右节点
if(cur.left!=null){
queue.offer(cur.left);
}
if(cur.right!=null){
queue.offer(cur.right);
}
}
// 返回结果
return count;
}
}
复杂度分析
时间复杂度:O(N)N为树节点个数
空间复杂度:O(N)N为树节点个数
👻方法3:DFS(深度优先)❌ 递归法
- 思路分析:节点个数=左节点个数+右节点个数+自身(左右中)
class Solution {
public int countNodes(TreeNode root) {
if(root == null) {
return 0;
}
int left = countNodes(root.left); // 左
int right = countNodes(root.right); // 右
return left+right+1; // 中(当前根节点的节点数量)
}
}
// 简化版本:
return root==null?0:countNodes(root.left)+countNodes(root.right)+1;
复杂度分析
时间复杂度:O(N)
空间复杂度:O(logN)空间占用取决于递归系统栈占用的空间
🟡13-二叉树的最近公共祖先(236)
1.题目内容
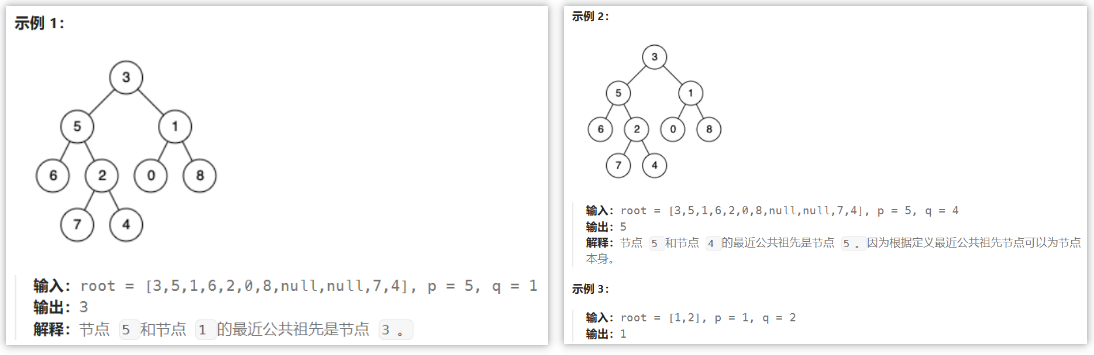
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
2.题解思路
👻方法1:分类讨论
- 思路分析:根据多种情况分析公共祖先节点可能出现的情况,递归判断
- 遍历每个节点,当节点左子树和右子树中同时包含p节点时和q节点时该节点即为最近公共祖先

PS:这种思路只能处理p、q在Tree中的情况,限定题目要求
/**
* 236 二叉树的最近公共祖先
*/
public class Solution1 {
/**
* 分类讨论:遍历节点进行讨论
* 1.node==null || node == p || node == q 则返回node
* 2.判断其是在左子树还是右子树:
* - 如果左右子树都找到,则当前node即为公共节点
* - 如果只有左子树找到,则返回findLeft(递归左子树的结果)
* - 如果只有右子树找到,则返回findRight(递归右子树的结果)
* - 如果左右子树都没找到,返回null
*/
public TreeNode lowestCommonAncestor(TreeNode node, TreeNode p, TreeNode q) {
// 递归退出条件
if (node == null) {
return null;
}
// 1.如果当前节点node为p或q,则node即为最小公共节点(结合案例可分析)
if (node == p || node == q) {
return node;
}
// 2.其他情况判断:继续判断公共节点是在左子树还是右子树
TreeNode findLeft = lowestCommonAncestor(node.left, p, q);
TreeNode findRight = lowestCommonAncestor(node.right, p, q);
// 判断左右子树的查找情况(要么在左子树、要么在右子树,要么左右子树都找到的情况下当前节点就是最小公共节点)
if (findLeft != null && findRight != null) {
return node; // 左右子树都找到了,则node就是当前的公共节点
}
if (findLeft != null) {
return findLeft; // 只有左子树找到了
}
if (findRight != null) {
return findRight; // 只有右子树找到了
}
return null; // 左右子树都没找到
}
}
复杂度分析
时间复杂度:
空间复杂度:
// 简化版本
/**
* 236 二叉树的最近公共祖先
*/
public class Solution2 {
/**
* 分类讨论:遍历节点进行讨论
* 1.node==null || node == p || node == q 则返回node
* 2.判断其是在左子树还是右子树:
* - 如果左右子树都找到,则当前node即为公共节点
* - 如果只有左子树找到,则返回findLeft(递归左子树的结果)
* - 如果只有右子树找到,则返回findRight(递归右子树的结果)
* - 如果左右子树都没找到,返回null
*/
public TreeNode lowestCommonAncestor(TreeNode node, TreeNode p, TreeNode q) {
// 1.node为null或者p、q中的任意一个节点则返回node
if (node == null || node == p || node == q) {
return node;
}
// 2.其他情况判断:继续判断公共节点是在左子树还是右子树
TreeNode findLeft = lowestCommonAncestor(node.left, p, q);
TreeNode findRight = lowestCommonAncestor(node.right, p, q);
// 判断左右子树的查找情况(要么在左子树、要么在右子树,要么左右子树都找到的情况下当前节点就是最小公共节点)
if (findLeft != null && findRight != null) {
return node;
}
return findLeft != null ? findLeft : findRight;
}
}
🚀二叉树层次遍历
🟡01-二叉树的右视图(199)
1.题目内容
给定一个二叉树的 根节点 root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。

2.题解思路
👻方法1:BFS(层次遍历)
- 思路分析:基于层次遍历的思路,可以看到所谓的右视图实际上就是拿到每一层的最后一个元素
- 基于此设定,可以将题意转化为层次遍历,然后分层遍历的时候判断是不是最后一个元素,如果是才加入结果集
/**
* 199 二叉树的右视图
*/
public class Solution1 {
/**
* 思路:基于层次遍历的思路(封装每一层最右侧的数)
*/
public List<Integer> rightSideView(TreeNode root) {
if(root==null){
return new ArrayList<>();
}
Deque<TreeNode> queue = new LinkedList<>(); // 辅助队列
queue.offer(root); // 初始化
// 定义右视图结果集
List<Integer> ans = new ArrayList<>();
// 遍历元素
while(!queue.isEmpty()){
// 分层统计
int size = queue.size();
for(int i=0;i<size;i++){
TreeNode node = queue.poll();
// 判断当前遍历元素是否为当层的最后一个元素
if(i==size-1){
ans.add(node.val); // 将当层的最后一个元素加入右视图结果集
}
// 将node的左右节点加入队列
if(node.left!=null){
queue.offer(node.left);
}
if(node.right!=null){
queue.offer(node.right);
}
}
}
// 返回结果
return ans;
}
}
复杂度分析
时间复杂度:O(N) N 树节点个数
空间复杂度:O(N)空间复杂度取决于队列占用(队列中的元素个数不会超过N)
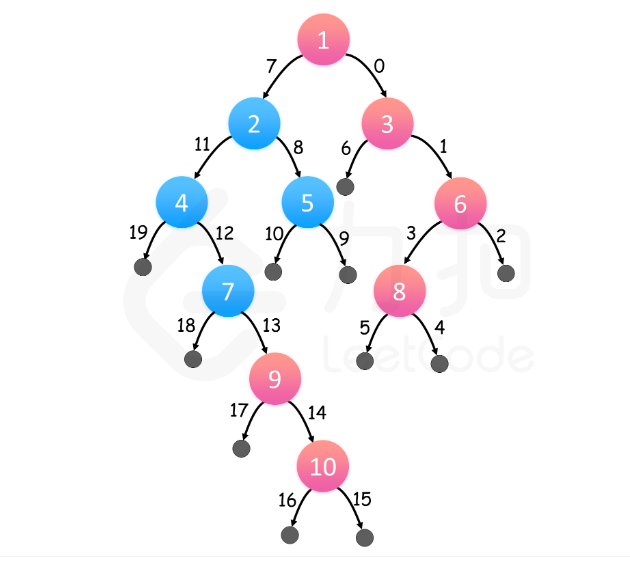
👻方法2:
- 思路分析:不能单纯用查找最右节点的思路去做,因为树的形状并无法确定
复杂度分析
时间复杂度:
空间复杂度:
🟢02-二叉树的层平均值(637)
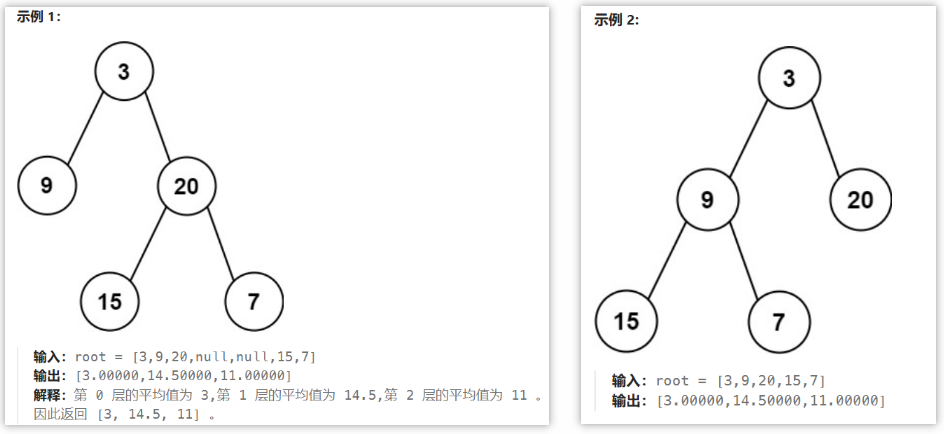
1.题目内容
给定一个非空二叉树的根节点 root , 以数组的形式返回每一层节点的平均值。与实际答案相差 10-5 以内的答案可以被接受。
2.题解思路
👻方法1:层序遍历(BFS)
/**
* 637 二叉树的层平均值
*/
public class Solution1 {
/**
* 基于层序遍历的思路
*/
public List<Double> averageOfLevels(TreeNode root) {
if (root == null) {
return new ArrayList<>();
}
// 存储每一层的平均值结果
List<Double> ans = new ArrayList<>();
Deque<TreeNode> queue = new LinkedList<>(); // 定义辅助队列
queue.offer(root); // 初始化
while (!queue.isEmpty()) {
// 分层
int size = queue.size();
// 计算每一层的平均值,并加入结果集
int curSum = 0;
for (int i = 0; i < size; i++) {
TreeNode node = queue.poll();
curSum += node.val; // 将每一层的元素值进行累加
// 将node的左右节点加入队列
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
}
// 单层遍历结束,计算平均值并加入结果集合
ans.add((double) curSum / size); // 平均值:和/元素个数
}
// 返回结果集
return ans;
}
}
复杂度分析
时间复杂度:O(N) N为树节点总数
空间复杂度:O(N) 空间复杂度取决于队列层次遍历占用(队列长度不会超出N)
🟡03-二叉树的层序遍历(102)
1.题目内容
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)
2.题解思路
👻方法1:BFS(层序遍历)
/**
* 102 层序遍历
*/
public class Solution1 {
/**
* 层序遍历:逐层遍历
*/
public List<List<Integer>> levelOrder(TreeNode root) {
// 空节点校验
if (root == null) {
return new ArrayList<>();
}
Deque<TreeNode> queue = new LinkedList<>(); // 定义辅助队列
queue.offer(root); // 初始化
// 定义结果集
List<List<Integer>> ans = new ArrayList<>();
// 遍历队列元素,直至队列为空
while (!queue.isEmpty()) {
// 分层遍历
List<Integer> curList = new ArrayList<>();
int curSize = queue.size();
for (int i = 0; i < curSize; i++) {
// 取出节点
TreeNode node = queue.poll();
// 将结果加入集合
curList.add(node.val);
// 将node的左右节点加入队列
if (node.left != null) {
queue.add(node.left);
}
if (node.right != null) {
queue.add(node.right);
}
}
// 单层遍历结束,录入结果集
ans.add(curList);
}
// 返回结果集
return ans;
}
}
复杂度分析
时间复杂度:O(N) N为树节点总数
空间复杂度:O(N) 空间复杂度取决于队列层次遍历占用(队列长度不会超出N)
🟡04-二叉树的锯齿形层序遍历(103)
1.题目内容
给你二叉树的根节点 root ,返回其节点值的 锯齿形层序遍历 。(即先从左往右,再从右往左进行下一层遍历,以此类推,层与层之间交替进行)。
2.题解思路
👻方法1:层序遍历
思路分析:基于层序遍历思想,通过定义一个反转标识来确定每一层遍历的方向
易错点(确保整体反序,而非局部反序):此处可能会思考在加入节点的时候根据遍历方向决定
先左后右还是先右后左,但如果在for循环中加入节点的时候根据遍历方向加入的话,处理不当则会出现局部方向的问题(因为节点的遍历是按顺序取出的)例如
[1,2,3,4,null,null,5]遍历第3层的时候就出现问题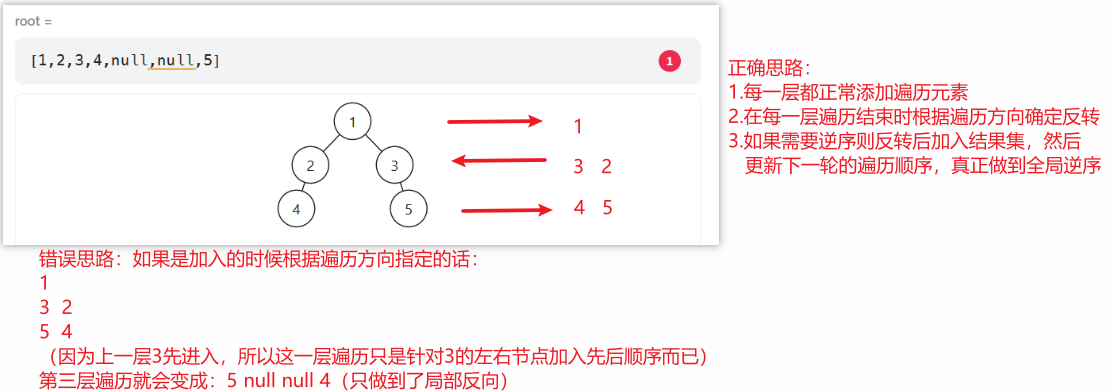
public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
if (root == null) {
return new ArrayList<>();
}
List<List<Integer>> ans = new ArrayList<>();
Deque<TreeNode> queue = new LinkedList<>(); // 定义辅助队列
queue.offer(root); // 初始化
boolean leftToRight = false; // true:从左到右;false:从右到左 (因为初始化的时候已经是从左到右的顺序,因此此处初始化为false)
// 遍历队列元素
while (!queue.isEmpty()) {
// 分层遍历
List<Integer> curList = new ArrayList<>();
int curSize = queue.size();
for (int i = 0; i < curSize; i++) {
// 取出节点
TreeNode node = queue.poll();
curList.add(node.val);
// 加入左右节点(正常录入节点)
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
}
if (leftToRight) {
Collections.reverse(curList);
}
ans.add(curList); // 当层遍历完成,加入结果集(判断是否需要对当层数据结果反转)
leftToRight = !leftToRight; // 当层遍历完成,切换下一轮次的遍历顺序
}
// 返回遍历结果集
return ans;
}
复杂度分析
时间复杂度:O(N) N为树节点总数
空间复杂度:O(N) 空间复杂度取决于队列层次遍历占用(队列长度不会超出N)
🚀二叉搜索树
🟢01-二叉搜索树的最小绝对差(530)
1.题目内容
给你一个二叉搜索树的根节点 root ,返回 树中任意两不同节点值之间的最小差值 。
差值是一个正数,其数值等于两值之差的绝对值。

2.题解思路
👻方法1:中序遍历(dfs)+检索min
- 思路分析:充分利用二叉搜索树的特性:
左节点<根节点<右节点- 即二叉搜索树的中序遍历最终得到就是一个升序数组,而升序数组中绝对值差的最小值就是比较相邻两节点差值的绝对值,找出其中最小值
public class Solution1 {
public int getMinimumDifference(TreeNode root) {
List<Integer> list = new ArrayList<>();
ldr(root, list); // 中序遍历
// 对中序遍历后的序列进行最小值绝对值判断(相邻两数比较)
int min = Integer.MAX_VALUE;
for (int i = 0; i < list.size() - 1; i++) {
min = Math.min(min, Math.abs(list.get(i + 1) - list.get(i)));
}
return min;
}
public void ldr(TreeNode node, List<Integer> list) {
if (node == null) {
return;
}
// 中序遍历(left=》root=》right)
ldr(node.left, list);
list.add(node.val);
ldr(node.right, list);
}
}
复杂度分析
- 时间复杂度:O(N)中序遍历需O(logN)时间复杂度,随后需对中序遍历的结果列表进行min检索
空间复杂度:O(N)需要额外列表存储中序遍历的结果
🟡02-二叉搜索树中第K小的元素(230)
1.题目内容
给定一个二叉搜索树的根节点 root ,和一个整数 k ,请你设计一个算法查找其中第 k 小的元素(从 1 开始计数)。
2.题解思路
👻方法1:中序遍历+检索k-1
- 思路分析:充分利用二叉搜索树的特性,二叉搜索树的中序遍历序列是一个连续升序的序列
- (1)获取二叉搜索树的中序序列(连续升序)
- (2)获取第K小的元素
- 不足:无法适配频繁地查找第 k 小的值,如果二叉搜索树频繁变化或者需要频繁查找这个第k小的元素,则这个方法不太适合
/**
* 230 二叉搜索树中第K小的元素
*/
public class Solution1 {
public int kthSmallest(TreeNode root, int k) {
List<Integer> list = new ArrayList<>();
ldr(root,list); // 获取中序遍历后的集合(升序集合)
return list.get(k-1); // 下标为k-1的元素即为第k小的元素
}
/**
* 中序遍历(left =》 root =》 right)
*/
public void ldr(TreeNode node, List<Integer> list){
if(node==null){
return;
}
ldr(node.left,list);
list.add(node.val);
ldr(node.right,list);
}
}
复杂度分析
时间复杂度:O(logN)中序遍历
空间复杂度:O(N)需要额外存储空间存储中序遍历结果
优化版本:不需要完整构建整个中序遍历序列,而是通过递归时计数统计,当达到K的时候返回结果
- 思路分析:定于全局变量用于递归计数统计、递归结果记录,在递归的过程中进行计数统计
/**
* 230 二叉搜索树中第K小的元素
*/
public class Solution3 {
// 定义全局变量用作递归计数统计、递归结果输出
int res, count;
public int kthSmallest(TreeNode root, int k) {
this.count = k; // 初始化count计数器,当计数器减为0表示找到这个第k小的元素
ldr(root); // 执行中序遍历,递归过程中进行计数
return res; // 返回结果
}
/**
* 中序遍历(left =》 root =》 right)
*/
public void ldr(TreeNode node) {
if (node == null) {
return;
}
ldr(node.left); // left
// 判断count计数是否达到k(count减为0)
if (count == 0) {
return;
} else {
// 记录值
res = node.val;
count--;
}
ldr(node.right); // right
}
}
👻方法2:中序遍历(迭代思路)
- 思路分析:考虑到如果需要频繁获取的话,采用迭代的思路进行中序遍历,这样可以在找到第K小的元素之后立刻停止,而不需要完整地遍历整棵树,以此降低复杂度
/**
* 230 二叉搜索树中第K小的元素
*/
public class Solution2 {
public int kthSmallest(TreeNode node, int k) {
Deque<TreeNode> stack = new ArrayDeque<>();
stack.push(node);
while (node!=null || !stack.isEmpty()) {
while (node != null) {
stack.push(node);
node = node.left;
}
// 当node为null(遍历到最左节点),此时弹出栈顶元素
node = stack.pop();
k--; // 计数-1(当K减为0,跳出循环)
if (k == 0) {
break;// 跳出循环,表示找到了这个第K小的元素
}
node = node.right;
}
// 当前指针指向的就是第K小的元素
return node.val;
}
}
复杂度分析
时间复杂度:O(H+k),其中 H 是树的高度。在开始遍历之前,我们需要 O(H) 到达叶结点。当树是平衡树时,时间复杂度取得最小值 O(logN+k);当树是线性树(树中每个结点都只有一个子结点或没有子结点)时,时间复杂度取得最大值 O(N+k)
空间复杂度:O(H),栈中最多需要存储 H 个元素。当树是平衡树时,空间复杂度取得最小值 O(logN);当树是线性树时,空间复杂度取得最大值 O(N)
🟡03-验证二叉搜索树(98)
1.题目内容
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树
有效 二叉搜索树定义如下:
节点的左子树只包含 小于 当前节点的数
节点的右子树只包含 大于 当前节点的数
所有左子树和右子树自身必须也是二叉搜索树
2.题解思路
👻方法1:中序遍历+升序判断
- 思路分析:充分利用二叉搜索树的特性,其中序遍历序列是一个连续序列
/**
* 098 验证二叉搜索树
*/
public class Solution1 {
public boolean isValidBST(TreeNode root) {
List<Integer> list = new ArrayList<>();
ldr(root, list); // 获取中序遍历结果
// 验证是否为BST(即验证是否连续升序)
for (int i = 0; i < list.size() - 1; i++) {
if (list.get(i) >= list.get(i + 1)) { // 出现降序(且二叉搜索树不能有相等的元素)
return false;
}
}
return true;
}
public void ldr(TreeNode node, List<Integer> list) {
if (node == null) {
return;
}
ldr(node.left, list);
list.add(node.val);
ldr(node.right, list);
}
}
复杂度分析
时间复杂度:
空间复杂度:
👻方法2:前中后序+递归判断
- 思路分析:基于前中后序的递归实现进行改造,在递归的过程中判断是否满足二叉搜索树的特点
- 前序:
- 中序:二叉搜索树的特性决定它的中序就是从小到大排列的, 所以每次只需要跟前一个遍历的节点比是不是比它大即可,通过pre记录前一个遍历的节点值
- 后序:
前序遍历
/**
* 098 验证二叉搜索树
*/
public class Solution2 {
/**
* 递归方式:前序遍历
* 此处用long接收参数(避免数值溢出问题)
* 因为二叉搜索树序满足:left < root < right 如果left取到int的最大值,那么root、right必须必这个MIN_INT要大,不符合场景,因此需要用long
*/
public boolean isValidBST(TreeNode root) {
return validBSTByPreOrder(root, Long.MIN_VALUE, Long.MAX_VALUE);
}
public boolean validBSTByPreOrder(TreeNode node, long leftVal, long rightVal) {
if (node == null) {
return true;
}
long x = node.val;
// 比较值,先递归左子树,后递归右子树
return leftVal < x && x < rightVal && validBSTByPreOrder(node.left, leftVal, x) && validBSTByPreOrder(node.right, x, rightVal);
}
}
复杂度分析
时间复杂度:O(n) n 为二叉搜索树节点个数
空间复杂度:O(n)最坏情况下二叉搜索树会退化成一条链表(因为题目中并没有保证这是一个平衡树),因此递归空间最坏可能会达到O(n)
中序遍历
/**
* 098 验证二叉搜索树
*/
public class Solution3 {
long pre = Long.MIN_VALUE;
/**
* 递归方式:中序遍历
*/
public boolean isValidBST(TreeNode root) {
return validBSTByInOrder(root);
}
public boolean validBSTByInOrder(TreeNode node) {
if (node == null) {
return true;
}
if(!validBSTByInOrder(node.left) || node.val <= pre){
return false;
}
pre = node.val;
return validBSTByInOrder(node.right);
}
}
复杂度分析
时间复杂度:O(n) n 为二叉搜索树节点个数
空间复杂度:O(n)最坏情况下二叉搜索树会退化成一条链表(因为题目中并没有保证这是一个平衡树),因此递归空间最坏可能会达到O(n)
后序遍历
/**
* 098 验证二叉搜索树
*/
public class Solution4 {
/**
* 递归方式:后序遍历
*/
public boolean isValidBST(TreeNode root) {
return dfs(root)[1] != Long.MAX_VALUE;
}
private long[] dfs(TreeNode node) {
if (node == null) {
return new long[]{Long.MAX_VALUE, Long.MIN_VALUE};
}
long[] left = dfs(node.left);
long[] right = dfs(node.right);
long x = node.val;
// 也可以在递归完左子树之后立刻判断,如果发现不是二叉搜索树,就不用递归右子树了
if (x <= left[1] || x >= right[0]) {
return new long[]{Long.MIN_VALUE, Long.MAX_VALUE};
}
return new long[]{Math.min(left[0], x), Math.max(right[1], x)};
}
}
复杂度分析
时间复杂度:O(n) n 为二叉搜索树节点个数
空间复杂度:O(n)最坏情况下二叉搜索树会退化成一条链表(因为题目中并没有保证这是一个平衡树),因此递归空间最坏可能会达到O(n)
