跳至主要內容

ext-01-数据结构设计

holic-x...大约 13 分钟算法算法

难度说明：🟢简单🟡中等🔴困难

学习资料

学习目标

  • 掌握数据结构核心基础
  • 借助数据结构完成常见题型

ext-01-数据结构设计

核心内容

​ 针对一些常见的数据结构和应用场景的设计思路剖析，如何借助现有的数据结构实现常用的场景结构，数据结构之间如何进行转化

  • LRUCache（最近最少使用缓存）：LinkedHashMap
  • 队列和栈：
    • 如何用队列实现栈？=》双队列思路（头插概念）
    • 如何用栈实现队列？=》双栈思路（输入栈、输出栈）
  • xxxx

理论基础

1.核心理论

2.技巧总结

常见题型

🟡146-LRU缓存

1.题目内容open in new window

请你设计并实现一个满足 LRU (最近最少使用) 缓存open in new window 约束的数据结构。

实现 LRUCache 类：

  • LRUCache(int capacity) 以 正整数 作为容量 capacity 初始化 LRU 缓存
  • int get(int key) 如果关键字 key 存在于缓存中，则返回关键字的值，否则返回 -1 。
  • void put(int key, int value) 如果关键字 key 已经存在，则变更其数据值 value ；如果不存在，则向缓存中插入该组 key-value 。如果插入操作导致关键字数量超过 capacity ，则应该 逐出 最久未使用的关键字。

函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。

示例：

输入
["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
输出
[null, null, null, 1, null, -1, null, -1, 3, 4]

解释
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // 缓存是 {1=1}
lRUCache.put(2, 2); // 缓存是 {1=1, 2=2}
lRUCache.get(1);    // 返回 1
lRUCache.put(3, 3); // 该操作会使得关键字 2 作废，缓存是 {1=1, 3=3}
lRUCache.get(2);    // 返回 -1 (未找到)
lRUCache.put(4, 4); // 该操作会使得关键字 1 作废，缓存是 {4=4, 3=3}
lRUCache.get(1);    // 返回 -1 (未找到)
lRUCache.get(3);    // 返回 3
lRUCache.get(4);    // 返回 4

2.题解思路

思路梳理

​ 首先理解什么是LRU：Least Recently Used 最近最少使用，即当缓存域满了之后会通过这种算法优先淘汰最近最少使用的元素。可以有两种思路切入LRU的设计：

  • 思路①：基于访问频次（统计每个元素的访问频次，优先淘汰访问频次最小的元素）

    • 数据插入：判断是否超出阈值，如果超出阈值则淘汰访问频次最低的元素（进行替换），如果没有超出阈值则正常追加数据
    • 数据访问：更新记录访问频次

  • 思路②：基于队列处理（更新队列中元素的排列顺序，确定一端入队、一端出队，如果元素被访问则将其重新排到后面，让前面最近没被访问的元素优先出队）

    • 基于上述流程分析，优化LRU的设计思路，如何通过不记录访问频次的方式实现LRU？即类似排队的概念，选定一个方向进行淘汰，当数据被访问时就将其重新排到后面去，以此达到不记录访问频次就能实现LRU淘汰的效果 =》淘汰尾部的数据（尾部存储的是最久远访问的数据）、让活跃的节点移动到队列另一段
      • 淘汰谁？：采用头插法，确保最新插入的数据在头部，依次类推，当依次插入数据超出缓存阈值的时候，此时尾部的数据会被淘汰（就是最先插入的数据会被淘汰）
      • 如何更新访问频次？：此处没有访问频次的概念，而是将活跃的数据移动到另一端

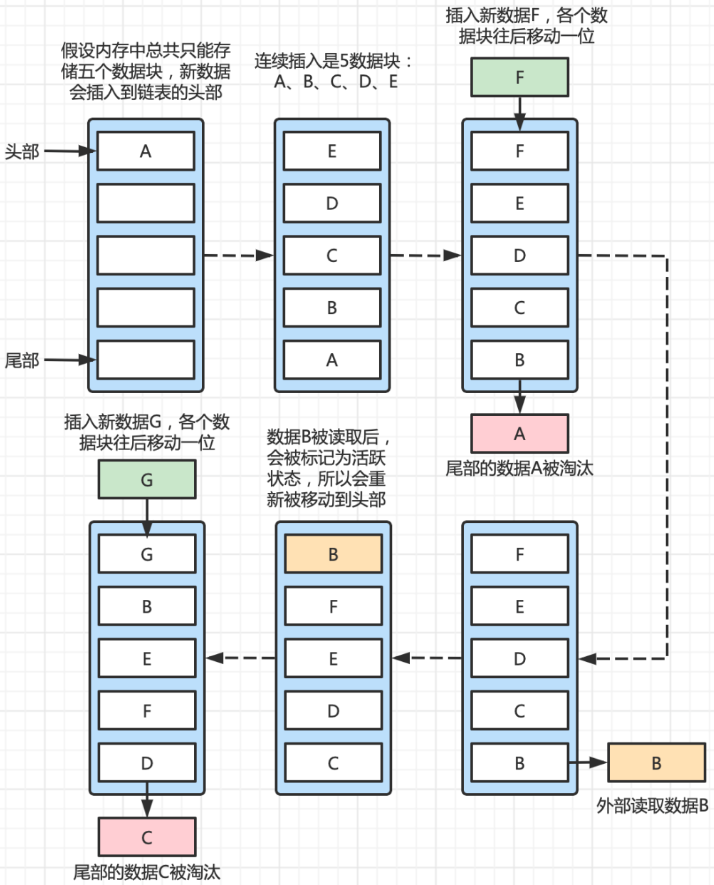
    image-20241223091802321

👻方法1：基于LinkedHashMap实现
  • 思路分析：基于队列（排队）概念处理，确定移除和新增的逻辑
    • 访问元素：如果元素存在则直接移除然后新增（调用新增元素方法），目的是为了让访问的元素
    • 新增元素：
      • 如果元素存在则覆盖并更新排列顺序（将其移动到队尾：先删除后新增）
      • 如果元素不存在则新增（需要校验容量值，如果超出容量则需淘汰队首元素（队首尾最近未被访问的元素），然后再执行新增）
/**
 * LRUCache：最近最少使用
 * 可以基于双向队列概念辅助处理：（此处用LinkedHashMap构建有序的k-v对）
 * ① put：访问（新增）：
 * - 如果元素不存在，直接追加尾部（追加的过程中需校验缓存是否超出阈值，如果超出则需弹出队首元素）
 * - 如果元素存在，删除元素并追加到尾部（追加的过程中需校验缓存是否超出阈值，如果超出则需弹出队首元素）
 * ② get：访问（获取）
 * - 如果元素不存在，不执行操作
 * - 如果元素存在，删除元素并追加到尾部（相当于更新元素的排序，将元素重新排到队尾）
 * ③ 初始化函数：根据限定容量大小控制存储集合
 */
class LRUCache {

    public int capacity;
    public LinkedHashMap<Integer, Integer> cache;

    LRUCache(int capacity) {
        this.capacity = capacity;
        this.cache = new LinkedHashMap<>();
    }

    int get(int key) {
        int val = -1;
        if (cache.containsKey(key)) {
            val = cache.get(key);
            cache.remove(key);
            // 此处调用put方法处理
            put(key, val);
        }
        return val;
    }

    void put(int key, int value) {
        // 如果已存在key则移除后添加
        if (cache.containsKey(key)) {
            cache.remove(key);
            cache.put(key, value);
        } else {
            // 新增新的key，校验容量
            if (cache.size() >= capacity) {
                // 移除队首元素随后加入新缓存
                int firstKey = cache.keySet().iterator().next();
                cache.remove(firstKey);
            }
            cache.put(key, value);
        }
    }

}

  • 复杂度分析

    • 时间复杂度：

    • 空间复杂度：

🟢232-用栈实现队列

1.题目内容open in new window

请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作（push、pop、peek、empty）：

实现 MyQueue 类：

  • void push(int x) 将元素 x 推到队列的末尾
  • int pop() 从队列的开头移除并返回元素
  • int peek() 返回队列开头的元素
  • boolean empty() 如果队列为空，返回 true ；否则，返回 false

说明：

  • 你 只能 使用标准的栈操作 —— 也就是只有 push to top, peek/pop from top, size, 和 is empty 操作是合法的。
  • 你所使用的语言也许不支持栈。你可以使用 list 或者 deque（双端队列）来模拟一个栈，只要是标准的栈操作即可。

示例 1：

输入：
["MyQueue", "push", "push", "peek", "pop", "empty"]
[[], [1], [2], [], [], []]
输出：
[null, null, null, 1, 1, false]

解释：
MyQueue myQueue = new MyQueue();
myQueue.push(1); // queue is: [1]
myQueue.push(2); // queue is: [1, 2] (leftmost is front of the queue)
myQueue.peek(); // return 1
myQueue.pop(); // return 1, queue is [2]
myQueue.empty(); // return false

2.题解思路

👻方法1：双栈思路（输入栈、输出栈）

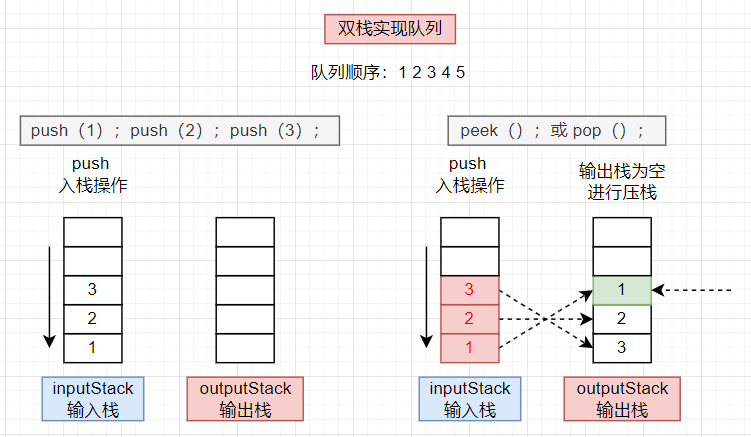
image-20241112104628081

  • 思路分析：构建双栈（输入栈inputStack、输出栈outputStack）
    • 输入栈：正常push数据
    • 输出栈：从栈顶获取元素（当输出栈为空的时候，需要将输入栈中现存的数据依次弹出然后压入输出栈）==负负得正：压入输入栈的时候先进后出，当从输入栈中弹出压入输出栈时原inputStack栈底的元素会被放到outputStack的栈顶，从而保证了输入的队列输出序列
    • 压栈时机：此处的压栈指的是当输出栈为空的时候，需要将输入栈中现存的数据依次弹出然后压入输出栈，因此此处可以有两种压栈时机
      • push的时候❌：每次压入数据的时候，每次压入数据都倒一次或者限定outputStack为空则倒一次
      • pop或peek的时候🟢：只在获取元素的时候当outputStack为空的时候进行压栈操作（只有当inputStack、outputStack不为空的时候整个队列才不为空）
    • empty：队列中的元素针对的是输入栈和输出栈的内容，由于优化处理选择的outputStack的压栈时机不同，所以不能进行校验输出栈是否为空（有可能此时输入栈不为空但还没压栈），所以队列不为空应该是两个栈都不为空的情况下才成立
/**
 * 232 用栈实现队列
 */
class MyQueue2 {

    // 双栈模拟
    Stack<Integer> inputStack; // 输入栈
    Stack<Integer> outputStack; // 输出栈

    // 初始化
    public MyQueue2() {
        inputStack = new Stack<>();
        outputStack = new Stack<>();
    }

    // 加入元素（往输入栈中插入）
    public void push(int x) {
        inputStack.push(x);
    }

    // 获取元素（从输出栈中获取，如果输出栈为空校验输入栈是否还有没遍历的数据，将输入栈现存数据压入输出栈）
    public int pop() {
        boolean isOutputStackEmpty = outputStack.isEmpty();
        if (isOutputStackEmpty) {
            // 输出栈为空，触发输入栈的压栈操作
            while (!inputStack.isEmpty()) {
                outputStack.push(inputStack.pop());
            }
        }
        // 弹出栈顶元素
        return outputStack.pop();
    }

    // 获取元素（不弹出元素）
    public int peek() {
        boolean isOutputStackEmpty = outputStack.isEmpty();
        if (isOutputStackEmpty) {
            // 输出栈为空，触发输入栈的压栈操作
            while (!inputStack.isEmpty()) {
                outputStack.push(inputStack.pop());
            }
        }
        // 获取栈顶元素
        return outputStack.peek();
    }

    // 队列为空判断
    public boolean empty() {
        // 当输入栈和输出栈都为空说明队列为空
        return inputStack.isEmpty() && outputStack.isEmpty();
    }
}

  • 复杂度分析

    • 时间复杂度：push和empty为O（1），pop 和 peek 为均摊 O(1)。对于每个元素，至多入栈和出栈各两次，故均摊复杂度为 O(1)

    • 空间复杂度：O(n)。其中 n 是操作总数。对于有 n 次 push 操作的情况，队列中会有 n 个元素，故空间复杂度为 O(n)

👻方法2：Deque（队列方法调用）
  • 思路分析：借助Deque双端队列的操作方法实现
    • 画图理解每个方法的执行效果，选用合适的方法组合实现栈或队列效果
/**
 * 232 用栈实现队列
 */
class MyQueue1 {

    // 双端队列模拟
    Deque<Integer> deque ;

    // 初始化
    public MyQueue1() {
        deque = new ArrayDeque<>();
    }

    // 加入元素
    public void push(int x) {
        deque.offerFirst(x);
    }

    public int pop() {
        return deque.pollLast();
    }

    public int peek() {
        return deque.peekLast();
    }

    public boolean empty() {
        return deque.isEmpty();
    }
}

  • 复杂度分析

    • 时间复杂度：

    • 空间复杂度：

🟢225-用队列实现栈

1.题目内容open in new window

请你仅使用两个队列实现一个后入先出（LIFO）的栈，并支持普通栈的全部四种操作（push、top、pop 和 empty）。

实现 MyStack 类：

  • void push(int x) 将元素 x 压入栈顶。
  • int pop() 移除并返回栈顶元素。
  • int top() 返回栈顶元素。
  • boolean empty() 如果栈是空的，返回 true ；否则，返回 false 。

注意：

  • 你只能使用队列的标准操作 —— 也就是 push to back、peek/pop from front、size 和 is empty 这些操作。
  • 你所使用的语言也许不支持队列。 你可以使用 list （列表）或者 deque（双端队列）来模拟一个队列 , 只要是标准的队列操作即可。

2.题解思路

👻方法1：双队列（主队列(栈核心)、辅助队列头插）
image-20241112104600439
  • 思路分析：采用双队列的思路实现（queue1、queue2，类似头插的概念，每次将最新的数据插入到现有队列的头部：先插入queue2，然后将queue1的队列插入到queue2，最后交换queue1和queue2（相当于queue1每次保存了最新的"栈"数据，而queue2是作为头插的辅助））
/**
 * 225 用队列实现栈（双队列、头插法思路）
 */
public class MyStack {

    LinkedList<Integer> queue1; // queue1 保存最新的"模拟栈"数据
    LinkedList<Integer> queue2; // queue2 作为头插的辅助队列

    // 初始化
    public MyStack() {
        queue1 = new LinkedList<>();
        queue2 = new LinkedList<>();
    }

    // 插入元素：类似头插概念
    public void push(int x) {
        // 1.将元素先插入到queue2
        queue2.offer(x);
        // 2.将queue1队列中现有元素依次补到queue2中，即确保最新插入的数据始终在队头（满足后入先出）
        while(!queue1.isEmpty()){
            queue2.offer(queue1.poll());
        }
        // 3.交换queue1、queue2，让queue1始终保存最新的"模拟栈"数据（即保存经过头插后的内容）
        LinkedList<Integer> temp = queue1;
        queue1 = queue2;
        queue2 = temp;
        // 交换两个队列指针（也可以直接让mainQueue指向tempQueue，然后tempQueue重置）
        // mainQueue = tempQueue;
        // tempQueue = new LinkedList<>();
    }

    // 弹出元素：从queue1中获取
    public int pop() {
        return queue1.poll();
    }

    // 返回栈顶元素：此处对应queue1最新头插的队首元素
    public int top() {
        return queue1.peek();
    }

    // 栈是否为空：queue1始终指向最新的模拟栈内容，因此此处只需要校验queue
    public boolean empty() {
        return queue1.isEmpty();
    }

}

  • 复杂度分析

    • 时间复杂度：入栈操作 O(n)，其余操作都是 O(1)，其中 n 是栈内的元素个数。
      • 入栈操作需要将 queue1中的 n 个元素出队，并入队 n+1 个元素到 queue2，共有 2n+1 次操作，每次出队和入队操作的时间复杂度都是 O(1)，因此入栈操作的时间复杂度是 O(n)
      • 出栈操作对应将 queue1的队首元素出队，时间复杂度是 O(1)
      • 获得栈顶元素操作对应获得 queue1 的队首元素，时间复杂度是 O(1)
      • 判断栈是否为空操作只需要判断 queue1是否为空，时间复杂度是 O(1)
    • 空间复杂度：O(n)，其中 n 是栈内的元素个数。需要使用两个队列存储栈内的元素
/**
 * 用队列实现栈：双队列实现（基于头插概念）
 */
class MyStack {

    public Queue<Integer> mainQueue; // 主队列：始终存储
    public Queue<Integer> tempQueue; // 辅助队列：用于头插构建,临时存储元素

    // 构造器
    public MyStack() {
        mainQueue = new LinkedList<>();
        tempQueue = new LinkedList<>();
    }

    // 将元素x压入栈顶
    public void push(int x) {
        // 插入过程：将元素插入tempQueue，然后将mainQueue中的元素追加到tempQueue后面，随后交换两个队列，始终让mainQueue指向完整的元素列表（即栈）
        tempQueue.offer(x);
        while (!mainQueue.isEmpty()) {
            tempQueue.offer(mainQueue.poll());
        }
        // 交换两个队列指针（也可以直接让mainQueue指向tempQueue，然后tempQueue重置）
        mainQueue = tempQueue;
        tempQueue = new LinkedList<>();
    }

    // 移除并返回栈顶元素
    public int pop() {
        // 返回并弹出mainQueue的队头元素（即对应头插后构成的栈的栈顶元素）
        return mainQueue.poll();
    }


    // 返回栈顶元素
    public int top() {
        // 返回mainQueue的队头元素（即对应头插后构成的栈的栈顶元素）
        return mainQueue.peek();
    }

    // 如果栈为空则返回true，否则返回false
    public boolean empty() {
        // 限定mainQueue即为对应的栈，因此此处只需要校验mainQueue是否为空
        return mainQueue.isEmpty();
    }
}
👻方法2：双端队列
  • 思路分析：借助双端队列提供的队列方法实现栈操作
/**
 * 225 用队列实现栈
 */
public class MyStack2 {

    Deque<Integer> deque;

    // 初始化
    public MyStack2() {
        deque = new LinkedList<>();
    }

    // 插入元素：
    public void push(int x) {
        deque.offerLast(x); // 队尾追加最新的元素
    }

    // 弹出元素：
    public int pop() {
        return deque.pollLast(); // 队尾获取最新的元素（满足LIFO）
    }

    // 返回栈顶元素：
    public int top() {
        return deque.peekLast();
    }

    // 栈是否为空：校验deque集合
    public boolean empty() {
        return deque.isEmpty();
    }

}

  • 复杂度分析

    • 时间复杂度：

    • 空间复杂度：

01-xxx（123）

1.题目内容

2.题解思路

👻方法1：

  • 复杂度分析

    • 时间复杂度：

    • 空间复杂度：

0  字
评论
  • 按正序
  • 按倒序
  • 按热度
Powered by Waline v3.1.3
一人の境 Copyright © 2019-未知 holic-x
Copyright © 2025 holic-x