难度说明：🟢简单🟡中等🔴困难

学习资料

• 代码随想录

学习目标

• 掌握数据结构核心基础
• 借助数据结构完成常见题型

skill-05-双指针

理论基础

1.核心理论

​ 双指针算法并不隶属于某一种数据结构，在数组、链表、字符串中都用到了双指针的思路，选择合适的方案解决算法问题，而不局限于数据结构

​ 双指针的效率优势：通过两个指针在一个for循环中完成两个for循环的操作

2.技巧总结

数组篇

• 移除元素：原地移除数组上的元素（通过两个指针在一个for循环下完成两个for循环的工作）

字符串篇

• 字符串反转：定义两个指针分别从前后遍历交换元素（指针向中间靠拢）
• 替换数字：使用双指针填充字符串的方法（一个指针遍历源字符串，一个指针遍历填充位置

链表篇

• 链表反转：改变链表的next指向，不需开辟空间反转链表
• 环形链表：判断是否存在环、判断环的入口，借助快慢指针（龟兔赛跑的思路）

N 数之和篇

• 三数之和：先对数组进行排序，然后固定一位，然后借助双指针从剩余的数组元素中找符合条件的三元组（将O(n³)暴力检索降低至O(n²)）

• 四数之和：在三数之和的基础上构建，固定1位，再检索匹配的三元组（相当于固定两位+双指针找四元组）（将O(n⁴)暴力检索降低至O(n³)）

• ❌两数之和：由于两数之和需要记录索引位置，如果通过双指针思路去做需要先对数组进行排序，这个过程会打乱原有的索引排序，反而不太适合用双指针，而是用哈希表去做

常见题型

🟢027-移除元素

题目内容

2.题解思路

👻方法1：双指针+交换元素

• 思路分析：双指针+交换元素，将非val置换到后面去

/**
 * 027 移除元素
 */
public class Solution027 {

    /**
     * 双指针思路：left、right
     * left 指向当前等于val的元素位置（用于置换）、right 指向当前不等于val的元素位置
     * 交换元素，直到指针相遇
     */
    public int removeElement(int[] nums, int val) {
        // 定义双指针
        int left = 0, right = nums.length - 1;
        while (left <= right) {
            // 如果两个指针满足置换条件则进行交换，交换完毕指针靠拢
            if (nums[left] == val && nums[right] != val) {
                // 交换元素
                int temp = nums[left];
                nums[left] = nums[right];
                nums[right] = temp;
                // 指针靠拢
                left++;
                right--;
            } else if (nums[left] != val) {
                left++; // left指针前移，寻找下一个可置换的位置
            } else if (nums[right] == val) {
                right--; // right指针前移，寻找下一个可置换的位置
            }
        }
        // 返回不等于val的元素数量
        return left;
    }
}

• 复杂度分析

  • 时间复杂度：O（n）n 为数组长度

  • 空间复杂度：O（1）原地交换，只占用常数级别的空间（指针定义）

🟢344-反转字符串

题目内容

2.题解思路

👻方法1：双指针+交换元素

• 思路分析：双指针+依次交换头尾元素，交换完成双指针向中间靠拢

/**
 * 344 反转字符串
 */
public class Solution344 {

    /**
     * 双指针：left、right分别指向头尾元素，依次相互置换，置换完成指针向中间靠拢
     */
    public void reverseString(char[] s) {
        // 定义双指针
        int left = 0, right = s.length - 1;
        while (left < right) {
            // 交换元素
            char temp = s[left];
            s[left] = s[right];
            s[right] = temp;
            // 指针靠拢
            left++;
            right--;
        }
    }

}

• 复杂度分析

  • 时间复杂度：O（n）n为字符串长度

  • 空间复杂度：O（1）占用常数级别的空间，原地交换

⚽KMW054-替换数字

题目内容

2.题解思路

👻方法1：统计数字+扩容数组+双指针（一个遍历元素、一个填充数组）

• 思路分析：
  • （1）统计源字符串中数字个数cnt，用于数组扩容确定
  • （2）根据cnt进行数组扩容（分两个数组处理，也可以在一个数组上处理）
  • （3）填充数组：
    • 两个数组处理：一个用于遍历的targetArr源数组，一个用于填充的newArr新数组，依次遍历然后从左往右填充新数组即可
    • 一个数组处理：newArr基于targetArr构建，前部分为targetArr内容，后部分为扩容待填充部分。定义双指针从后往前遍历数组，一个指针用于指向当前遍历字符，一个指针用于指向当前填充的位置（选用从后往前的做法不用考虑从前往后填充导致的整体数组元素后移问题，也不用担心覆盖问题）

/**
 * 卡码网 054 替换数字
 */
public class SolutionKMW054 {

    /**
     * 将target中的数字置换为"number"：
     * （1）统计字符串中数字的个数cnt
     * （2）根据统计个数cnt扩容数组，通过双指针从后往前置换
     * - pointer：用于遍历元素；- cur：用于指向当前填充的位置
     */
    public String convertDigit(String target){
        // 1.统计字符串中数字的个数
        int cnt = 0; // 数字个数统计
        char[] targetArr = target.toCharArray();
        for(char ch : targetArr){
            if(Character.isDigit(ch)){
                cnt++;
            }
        }

        // 2.定义扩容数组，将源字符串数组copy进去
        char[] newArr = Arrays.copyOfRange(targetArr, 0,target.length() + 5 * cnt);
        // 遍历扩容后的新数组：pointer（从后往前遍历元素）、cur（从后往前填充元素）
        int cur = newArr.length -1;
        for(int pointer=target.length()-1;pointer>=0;pointer--){
            // 判断当前遍历元素是否为字母，如果为字母则直接填充
            char curCh = newArr[pointer];
            if(Character.isLetter(curCh)){
                newArr[cur--] = curCh;
            }else if(Character.isDigit(curCh)){
                // 如果为数字，则需逆序置换rebmun
                newArr[cur--] = 'r';
                newArr[cur--] = 'e';
                newArr[cur--] = 'b';
                newArr[cur--] = 'm';
                newArr[cur--] = 'u';
                newArr[cur--] = 'n';
            }
        }

        // 3.返回构建好的字符串
        return new String(newArr);
    }

    public static void main(String[] args) {
        String target = "a1b2c3";
        SolutionKMW054 solutionKMW054 = new SolutionKMW054();
        System.out.println(solutionKMW054.convertDigit(target));
    }

}

• 复杂度分析

  • 时间复杂度：O（m+n）n 为字符串长度，m设定为扩容数组的填充占用的时间复杂度

  • 空间复杂度：O（m）需结合数字个数进行数组扩容

🟡151-翻转字符串中的单词

题目内容

2.题解思路

👻方法1：去除首尾空格+切割+原地反转（双指针）+拼接

• 思路分析：
  • （1）去除字符串首尾空格
  • （2）切割字符串（\\s+，基于正则表达式，以一个或者多个空格进行切割）
  • （3）原地反转（基于双指针思路进行数组反转）
  • （4）拼接反转后的结果（通过String.join方法构建）

/**
 * 151 反转字符串中的单词
 */
public class Solution151 {

    public String reverseWords(String s) {
        // 1.取出元素首尾空格
        s = s.trim();
        // 2.切割字符串
        String[] strs = s.split("\\s+");
        // 3.交换字符串数组元素
        int left = 0,right = strs.length-1;
        while(left<right){
            // 交换元素
            String temp = strs[left];
            strs[left] = strs[right];
            strs[right] = temp;
            // 指针靠拢
            left++;
            right--;
        }
        // 4.将数组拼接
        return String.join(" ", strs);
    }
}

• 复杂度分析

  • 时间复杂度：O（n）需遍历所有字符串

  • 空间复杂度：O（n）需定义数组存储切割后的字符串数组，原地反转占用的是常数级空间

🟢206-翻转链表

题目内容

2.题解思路

👻方法1：双指针（prev+cur+nxt）

• 思路分析：核心在于让cur.next指向其前一个节点prev，在这个过程中需要先记录cur.next(nxt)，指针修改完成则继续下一个位置的指向修改（此时pre、cur都要向前移动，指向下一个位置：pre=cur、cur=nxt）

/**
 * 206 反转单链表
 */
public class Solution206 {

    /**
     * 链表反转：pre、cur、nxt
     * 核心：将cur.next指向pre，随后pre、cur指针后移，在此需注意先记录nxt（cur.next）
     */
    public ListNode reverseList(ListNode head) {
        // 定义虚拟头节点
        ListNode dummy = new ListNode(-1, head);
        ListNode cur = dummy.next; // cur 指向遍历指针
        ListNode pre = null; // pre 作为尾节点（初始化时）
        while (cur != null) {
            ListNode nxt = cur.next;
            cur.next = pre; // 将cur的next指针指向前一个节点
            // 双指针继续后移
            pre = cur;
            cur = nxt;
        }
        // 最终pre指向反转链表
        return pre;
    }

}

• 复杂度分析

  • 时间复杂度：O（n）n为链表长度

• 空间复杂度：O（1）只占用常数级别的空间

🟡019-删除链表的倒数第N个节点

题目内容

2.题解思路

👻方法1：双指针（快慢指针：fast先走n步，然后slow、fast同时出发）

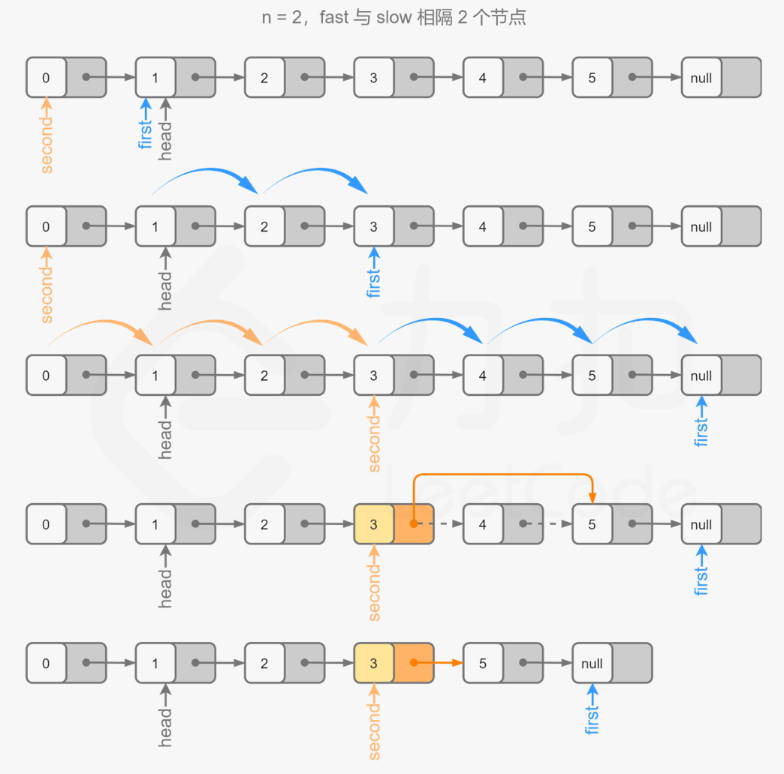
• 思路分析：巧妙利用快慢指针的思路（如果概念懵最好的解决方式就是画图理解）
  • 实现分析：对于链表head定义快慢指针，slow、fast初始化指向head
    • （1）fast指针先走n步
    • （2）随后slow、fast同时出发，当fast到达链表尾部的时候，此时slow也到达了第len-n的位置（也就是要删除的倒数第N个节点）
  • 进一步说明：由于删除节点是要找到待删除节点的前驱节点prev（然后直接执行prev.next=prev.next.next），因此此处如果slow能再晚一步出发，那么等到fast到达链表尾部的时候slow刚好就到达这个待删除的倒数第N个节点的前驱节点位置。因此dummy虚拟头节点就派上用场了，引入dummy=new ListNode(-1,head)，让slow初始化指向dummy那么就能达到目的
    • 此处虚拟头节点的引入有两个好处：
      • 不用考虑删除头节点的各种判断的苦恼（避免头节点NPE处理繁琐）
      • 让slow再慢一步出发，能够拿到待删除节点的前驱节点，更好地进行删除操作

/**
 * 019 删除链表的倒数第N个节点
 */
public class Solution019 {
    /**
     * 双指针：定义快慢指针
     * 1.快指针从head开始，让快指针先走n步   慢指针从起点（dummy）开始
     * 2.当快指针走了n步之后，双指针同时出发，当快指针走到链表尾部的时候此时慢指针恰好就走到倒数第n个节点
     */
    public ListNode removeNthFromEnd(ListNode head, int n) {
        // 构建虚拟头节点
        ListNode dummy = new ListNode(-1, head);
        // 定义双指针
        ListNode slow = dummy, fast = head; // slow初始指向dummy（是为了拿到待删除节点的前驱节点），fast初始指向head
        // 1.快指针先走n步
        for (int i = 0; i < n; i++) {
            fast = fast.next;
        }
        // 2.双指针再一起出发，当快指针遍历到链表尾部，此时慢指针指向len-n（倒数第n的位置）的前驱节点位置
        while (fast != null) {
            slow = slow.next;
            fast = fast.next;
        }
        // 删除指定节点
        slow.next = slow.next.next;
        // 返回
        return dummy.next;
    }
}

• 复杂度分析

  • 时间复杂度：O（n）双指针遍历链表，当fast遍历到链表尾部循环结束

  • 空间复杂度：O（1）只占用常数级别的空间

🟢160-链表相交

题目内容

2.题解思路

👻方法1：双指针（PA：A->B、PB：B->A 指针最终相遇为交点（公共交点或者null））

/**
 * 160 链表相交
 */
public class Solution160 {

    /**
     * 双指针遍历：pointerA(A->B) pointer(B->A)
     * 如果两个链表存在公共链表（公共交点），则两个指针同时出发遍历最终会相遇（相遇的点要么是公共交点要么是null）
     */
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        // 定义双指针遍历链表
        ListNode pointerA=headA;
        ListNode pointerB=headB;
        while(pointerA!=pointerB){
            // A指针遍历（A->B）
            if(pointerA!=null){
                pointerA = pointerA.next;// A指针继续往前
            }else{
                pointerA = headB; // 指向B链表继续遍历
            }

            // B指针遍历（B->A）
            if(pointerB!=null){
                pointerB = pointerB.next; // B指针继续往前
            }else{
                pointerB = headA; // 指向A链表继续遍历
            }
        }
        // 返回相遇点
        return pointerA;
    }
}

• 复杂度分析

  • 时间复杂度：O（m+n）m、n分别为两个链表的长度，最坏的情况是两个链表没有公共交点，双指针都遍历到尾部

  • 空间复杂度：O（1）占用常数级空间（双指针）

🟡142-环形链表II

题目内容

2.题解思路

👻方法1：快慢指针（龟兔赛跑）（判断是否存在环、获取环入口）

/**
 * 142 环形链表II（判断是否存在环，判断环入口）
 */
public class Solution142 {

    /**
     * 1.判断是否存在环（龟兔赛跑）：slow、fast起点相同，slow走一步，fast走两步
     * 2.如果存在环则获取环入口，让fast从起点、slow从当前位置一起出发，相遇位置即环入口
     */
    public ListNode detectCycle(ListNode head) {
        // head为空判断
        if (head == null) {
            return head;
        }

        ListNode slow = head;
        ListNode fast = head;
        boolean hasCycle = false;
        while (fast != null && fast.next != null) { // fast指针先遍历到链表尾部则循环结束
            slow = slow.next; // slow指针走1步
            fast = fast.next.next; // fast指针走2步
            // 判断是否相遇
            if (slow == fast) {
                hasCycle = true; // 存在环
                break; // 跳出当前循环，需要保留slow、fast当前位置
            }
        }

        // 判断是否存在环
        if (!hasCycle) {
            return null; // 不存在环直接返回
        }

        // 存在环：fast从起点、slow从当前位置继续同时同步出发，两者再次相遇即为入环口
        fast = head;
        while (fast != slow) {
            fast = fast.next;
            slow = slow.next;
        }
        // 返回入环口
        return slow;
    }

}

• 复杂度分析

  • 时间复杂度：O（n） n 为链表长度，需判断是否存在环，如果存在环还需继续遍历寻找环入口

• 空间复杂度：O（n）双指针法（龟兔赛跑），占用常数级空间

🟡015-三数之和

题目内容

2.题解思路

👻方法1：双指针（排序+固定1位+双指针检索三元组）

/**
 * 015 三数之和
 */
public class Solution015 {

    /**
     * 排序 + 双指针（固定1位+双指针寻找三元组）
     */
    public List<List<Integer>> threeSum(int[] nums) {
        // 定义结果集合
        List<List<Integer>> res = new ArrayList<>();

        // 1.对数组元素进行排序
        Arrays.sort(nums);

        // 2.双指针（固定1位+双指针寻找三元组）
        int len = nums.length;
        for (int i = 0; i < len - 2; i++) {
            // 特例情况判断
            if(nums[i]>0){
                break; // 如果固定的位置元素大于0，则后面累加和会更大，不可能构成三元组
            }

            // 定义双指针寻找三元组
            int left = i + 1, right = len - 1;
            while (left < right) { // 不能重复用数组元素
                // 判断当前三个元素和与0的关系，决定指针移动方向
                int curSum = nums[i] + nums[left] + nums[right];
                if (curSum == 0) {
                    // 满足三元组，判断去重条件决定是否加入结果集合
                    List<Integer> temp = new ArrayList<>();
                    temp.add(nums[i]);
                    temp.add(nums[left]);
                    temp.add(nums[right]);
                    if (!res.contains(temp)) {
                        res.add(temp);
                    }
                    // 处理完成，双指针向中间靠拢
                    left++;
                    right--;
                } else if (curSum > 0) {
                    // 当前curSum比较大，需让curSum变小
                    right--;
                } else if (curSum < 0) {
                    // 当前curSum比较小，需让curSum变大
                    left++;
                }
            }
        }
        // 返回最终的结果集
        return res;
    }
}

• 复杂度分析

  • 时间复杂度：O（n²）通过双指针将原O（n³）的复杂度优化到O（n²）

  • 空间复杂度：O（logN）如果不考虑结果集存储的占用空间，此处额外的空间占用主要是数组排序消耗

🟡018-四数之和

题目内容

2.题解思路

👻方法1：排序+双指针（固定2位+双指针（延续三元组思路）检索四元组）

/**
 * 018 四数之和
 */
public class Solution018 {

    /**
     * 排序 + 双指针（固定2位+双指针寻找四元组）
     */
    public List<List<Integer>> fourSum(int[] nums, int target) {
        // 定义结果集合
        List<List<Integer>> res = new ArrayList<>();

        // 1.对数组元素进行排序
        Arrays.sort(nums);

        // 2.双指针（固定1位+双指针寻找三元组）
        int len = nums.length;
        for (int i = 0; i < len - 3; i++) {
            for (int j = i + 1; j < len - 2; j++) {
                // 定义双指针寻找四元组
                int left = j + 1, right = len - 1;
                while (left < right) { // 不能重复用数组元素
                    // 判断当前四个元素和与target的关系，决定指针移动方向
                    int curSum = nums[i] + nums[j] + nums[left] + nums[right];
                    if (curSum == target) {
                        // 满足四元组，判断去重条件决定是否加入结果集合
                        List<Integer> temp = new ArrayList<>();
                        temp.add(nums[i]);
                        temp.add(nums[j]);
                        temp.add(nums[left]);
                        temp.add(nums[right]);
                        if (!res.contains(temp)) {
                            res.add(temp);
                        }
                        // 处理完成，双指针向中间靠拢
                        left++;
                        right--;
                    } else if (curSum > target) {
                        // 当前curSum比较大，需让curSum变小
                        right--;
                    } else if (curSum < target) {
                        // 当前curSum比较小，需让curSum变大
                        left++;
                    }
                }
            }
        }
        // 返回最终的结果集
        return res;
    }
}

• 复杂度分析

  • 时间复杂度：O（n³）通过双指针将原O（n⁴）的复杂度优化到O（n³）

  • 空间复杂度：O（logN）如果不考虑结果集存储的占用空间，此处额外的空间占用主要是数组排序消耗