skill-09-贪心算法

holic-x...大约 67 分钟

难度说明：🟢简单🟡中等🔴困难

学习资料

代码随想录open in new window

学习目标

掌握数据结构核心基础
借助数据结构完成常见题型

skill-09-贪心算法

理论基础

1.核心理论

贪心的本质：通过选择每一阶段的局部最优，从而达到全局最优

举个例子：如果有一堆钞票，可以拿走10张，如果想要达到最大的金额，要怎么拿？最贪心的做法就是每次拿最大的（局部最优），进而达到全局最优

贪心算法的本质即难点，很难从题目中去分析如何从局部最优推出全局最优，甚至没有固定的策略或者套路。如果采用手动模拟的思路，模拟可行的话可以试试看贪心算法，但是如果模拟不可行则可能需要切换动态规划思路

而验证贪心算法的正确性往往也是最难的，但要想推翻贪心算法策略最好用的方式就是通过举反例来推翻

但往往通过手动模拟或者举例子得出的结论可能可靠性并没有那么强，有时候可能需要数学证明（数学归纳法、反证法）来进行作证。但一般情况下不会现场让证明贪心算法的合理性，只要通过测试用例、能够自圆其说即可。因为贪心有时候更多的是一种常识性的引导，因此在刷题的时候如果发现一些题目可以通过手动模拟或者举例子（枚举）的方式来从局部最优得到全局最优的情况下，而且没有反例可推翻时，可以试着用贪心算法去解决

2.技巧总结

贪心算法的解题步骤

将问题分解为若干个子问题
找出适合的贪心策略
求解每一个子问题的最优解
将局部最优解堆叠成全局最优解

上述的步骤有点趋向理论化，平时的场景中如果单纯从理论去切入很容易陷进去（略显积累），倒不如切入重点，理解清楚"局部最优"是什么？可否推导出"全局最优"，从这两个核心点去靠的话可能解题的目的性会更强一点

总而言之，贪心无技巧，它就是一个常识性推导和举反例的过程，解题步骤有时会比较抽象，没有那么多套路和模板

题解核心

基础问题：

455-分发饼干：排序+双指针+贪心（用小的饼干投喂胃口小的小朋友，直到饼干派完或者小朋友都轮到了）
1005-K次取反后最大化的数组和：
- 排序 + 负数取反 + 根据奇偶处理余K：核心是尽量将小的负数取反，根据余K的奇偶性判断做取反处理
- 堆 + 取反（根据K）：数据入堆（自动维护数据顺序），取堆顶元素如果是负数就取反执行K次
860-柠檬水找零：关注散纸的剩余张数，遍历所有账单，判断是否可以找零并选择找零方案（贪心思路：尽量保留更多的5元）

序列问题：

376-摆动序列：贪心（峰谷切换问题）
- preDiff与curDiff的情况讨论（两者方向相反，则可将当前元素加入），贪心的目的在于不断加入满足条件的峰、谷
738-单调递增的数字：逆序找非单调递增的位置执行-1，记录位置idx；遍历完成后将idx+1位置开始的数字置为9

股票问题：

121-买卖股票的最佳时机："低买高卖"：假设【以当日价格卖出，历史最低价买入】计算日内利润，获取最大的日内利润
122-买卖股票的最佳时机II："做T利润收集"：计算每日做T可以得到的"正利润"，差价为负则不做任何操作，差价为正则收集，进而得到整个周期的总利润

加油站问题：找到可行的加油站起点（中间不能断油）+ 能跑完一圈（所有加油站遍历完成总油量仍有剩余）

区间问题：

045-跳跃游戏：区间覆盖（在遍历过程中更新"右边界"（每次选择更大的覆盖范围））
452-用最少的箭引爆更多的气球：右边界排序+右端点射击（遍历排序后的区间，判断上一个引爆点是否覆盖当前区间，如果未覆盖则选择右端点作为新的引爆点）
435-无重叠区间：思路和【452-用最少的箭引爆更多的气球】类似，只不过此处需要判断的是重复区间的个数，且需要注意临界问题（触点不视作覆盖）
763-划分字母区间：通过字符出现最远距离取并集的方法，把出现过的字符都圈到一个区间里（找可能的切割点，当遍历位置=目前已遍历的字母的最远出现位置时进行切割）
056-合并区间：左边界排序、右边界扩展（判断是否覆盖，是否需要扩展）

两个维度权衡问题：

135-分发糖果：两次遍历（动态规划+贪心算法）将【相邻两个孩子评分更高的孩子会获得更多的糖果】拆分为左右规则进行校验，选择同时满足两个规则的糖果数（此处的思路有点类似【求左右乘积】的动态规划思路）
406-根据身高重建队列：联合排序（先h后k）+ 遍历并按k插入

常见题型

📯基础题型

🟢455-分发饼干

1.题目内容open in new window

假设你是一位很棒的家长，想要给你的孩子们一些小饼干。但是，每个孩子最多只能给一块饼干。

对每个孩子 i，都有一个胃口值 g[i]，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j，都有一个尺寸 s[j] 。如果 s[j] >= g[i]，我们可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。你的目标是满足尽可能多的孩子，并输出这个最大数值

示例 1:

输入: g = [1,2,3], s = [1,1]
输出: 1
解释: 
你有三个孩子和两块小饼干，3 个孩子的胃口值分别是：1,2,3。
虽然你有两块小饼干，由于他们的尺寸都是 1，你只能让胃口值是 1 的孩子满足。
所以你应该输出 1。

示例 2:

输入: g = [1,2], s = [1,2,3]
输出: 2
解释: 
你有两个孩子和三块小饼干，2 个孩子的胃口值分别是 1,2。
你拥有的饼干数量和尺寸都足以让所有孩子满足。
所以你应该输出 2。

2.题解思路

👻方法1：贪心（排序+双指针+贪心）

思路分析：是否可以派发饼干取决于饼干大小是否满足小朋友的胃口，每个小朋友只能得到一块饼干，且一块饼干只能派给一个小朋友。因此最贪心的思路就是用最小的饼干投喂胃口最小的小朋友
- 排序：分别对两个数组进行排序（从小到大）
- 双指针：定义双指针分别辅助遍历饼干大小数组s[]和小朋友胃口数组g[]（两个数组数量不一定相等）
- 贪心遍历：同时遍历两个数组（由于两个数组数量不一定相等，因此此处设定结束条件是两个数组中其中一个遍历结束就整体结束），判断当前sPointer指向的饼干是否可以派给gPointer指向的小朋友
  - 如果可以s[sPointer]>=g[gPointer]：记录结果，两个指针继续后移等待下一轮判断
  - 如果不行s[sPointer]<g[gPointer]：说明当前饼干不满足这个目前胃口最小的小朋友的要求（更别说后面比他大胃口的小朋友了），因此这块饼干派不出去，只能sPointer++取下一块再继续判断

/**
 * 455 分发饼干
 */
public class Solution1 {
    public int findContentChildren(int[] g, int[] s) {
        // 记录满足派发条件的个数
        int cnt = 0;

        // 排序
        Arrays.sort(g);
        Arrays.sort(s);

        // 定义双指针：分别指向两个数组遍历位置
        int gPointer = 0, sPointer = 0;
        // 饼干和小朋友的数量不一定一一对应，因此两个当中一个完结视为结束
        while (sPointer < s.length && gPointer < g.length) {
            // 用最小的饼干投喂胃口最小的小朋友
            if (s[sPointer] >= g[gPointer]) {
                // 满足条件则进行投喂，然后继续下一块饼干的派发
                cnt++;
                // 继续下一块饼干、下一个小朋友
                sPointer++;
                gPointer++;
            } else {
                // 当前饼干不满足投喂这个小朋友，拿下一块试试
                sPointer++;
            }
        }

        // 返回结果
        return cnt;
    }
}

复杂度分析
- 时间复杂度：双数组排序+双数组遍历 =》O(mlogm+nlogn)，其中 m 和 n 分别是数组 g 和 s 的长度。对两个数组排序的时间复杂度是 O(mlogm+nlogn)，遍历数组的时间复杂度是 O(m+n)，因此总时间复杂度是 O(mlogm+nlogn)
空间复杂度：O(logm+logn) 主要是额外排序的空间开销

🟢1005-K次取反后最大化的数组和

1.题目内容open in new window

给你一个整数数组 nums 和一个整数 k ，按以下方法修改该数组：

选择某个下标 i 并将 nums[i] 替换为 -nums[i] 。

重复这个过程恰好 k 次。可以多次选择同一个下标 i 。

以这种方式修改数组后，返回数组 可能的最大和 。

示例 1：

输入：nums = [4,2,3], k = 1
输出：5
解释：选择下标 1 ，nums 变为 [4,-2,3] 。

示例 2：

输入：nums = [3,-1,0,2], k = 3
输出：6
解释：选择下标 (1, 2, 2) ，nums 变为 [3,1,0,2] 。

示例 3：

输入：nums = [2,-3,-1,5,-4], k = 2
输出：13
解释：选择下标 (1, 4) ，nums 变为 [2,3,-1,5,4] 。

2.题解思路

贪心思路：此处贪心的核心思路是尽可能对小数进行取反（因为更小的负数取反会更大，而更小的正数区分扣减的没那么多，因此优先每次选择最小的数进行取反即可），但此处有一个点在于负数取反后重新放入数组可能会打乱原有的排序，因此如果仅仅依靠数组遍历则需分情况讨论：

思路1（排序+取反）
- ① 对数组进行排序
- ② 遍历一遍数组，在k次限定条件下对负数进行取反（有可能出现所有负数都取反完成的情况，有可能k有剩余），并在此过程中计算目前的累加和sum
- ③ k的剩余处理：
  - 如果k无剩余，则步骤②中得到的结果sum即为所求；
  - 如果k有剩余，则分奇偶性讨论（偶数则一正一负操作抵消返回sum，奇数则需要获取当前的数组的最小值进行取反得到sum-2*min）
思路2（最小堆）：上述步骤③中还涉及到一次排序/遍历操作找到最小值，主要原因是因为取反操作打乱了原有的数组排序，因此需要获取min(或者在步骤②的遍历过程中同步更新目前的min)
- ① 构建最小堆维护数组元素
- ② k次取反：每次选择目前堆中的最小元素（堆顶元素）进行取反后重新载入堆（堆自动维护了元素的有序性，确保每次取出的堆顶元素是min，因此无序额外排序）
- ③ 弹出堆元素，获取累加和

👻方法1：贪心算法（排序+取反）

贪心思路分析

排序分析：只有将负数取反才可能拿到最大和，且负数越小其取反的收益越大，因此可以先将数据按照【从小到大】的顺序进行排序，然后按顺序取反
取反过程：按照顺序，依次从最小的负数开始取反。此处根据【负数的个数】和【k的取值】有两种情况需要讨论（在处理的过程中关注k有没有用完）
- 如果负数够用（负数足够多，能满足k次反转）：那么在遍历过程中就能够满足反转（完成k次负数反转，其他元素不动），整个数组遍历完成就可取得目前的最大数组和
- 如果负数不够用（已经将数组中所有的负数都取反了）：则一次遍历将所有负数反转，并计算当前数组的最大和。然后根据剩余K的个数来决定接下来的取反操作
  - 如果剩余的K为偶数，由于此时数组中已经全部为正数，所以任意取正数一正一负抵消了，这个对curMaxSum没有影响
  - 如果剩余的K为奇数，由于此时数据中已经全部为正数，所以要从数组中取一个最小的正数取反（也就是说curMaxSum要减去两倍的这个最小整数，得到最终的结果）
    - 这个最小正数可以有两种方式获取：一种是最新的数组进行二次排序，然后取最小的；也可以在遍历的过程中记录这个min（注意负数取反）

public int largestSumAfterKNegations(int[] nums, int k) {
        int curMaxSum = 0; // 记录当前的最大数组和

        // 对数组元素进行从小到大排序
        Arrays.sort(nums);

        // 遍历数组，取负数进行取反（根据k进行处理）
        for (int i = 0; i < nums.length; i++) {
            // 如果是负数且K足够，则将元素取反
            if (nums[i] < 0 && k > 0) {
                nums[i] *= -1; // 负数取反
                k--; // k 减 1
            }
            // 计算累加和
            curMaxSum += nums[i];
        }

        /**
         * 剩余K为0，对curMaxSum无影响
         * 剩余K为大于0的偶数，一正一负抵消对curMaxSum无影响（因为此时数组已经没有负数可取反收益了，只能选择一正一负）
         * 剩余K为奇数，则需选择当前数组的最小正数来做 一正一负 + 一负 的操作，最终 curMaxSum 取的是 curMaxSum-2*最小正数
         */
        // 遍历完成，如果K仍有剩余则需进行处理（判断当前剩余K是奇数还是偶数）
        if (k % 2 == 0) {
            return curMaxSum;
        } else if (k % 2 == 1) {
            // 对元素进行排序，取到当前的最小整数
            Arrays.sort(nums);
            return curMaxSum - 2 * nums[0];
        }
        return curMaxSum;
    }

}

复杂度分析
- 时间复杂度：遍历+排序
- 空间复杂度：主要是排序占用的空间

思路：维护min

/**
 * 🟢 1005 K次取反后最大化的数组和 - https://leetcode.cn/problems/maximize-sum-of-array-after-k-negations/description/
 */
public class Solution1005_03 {

    /**
     * 思路分析：选择某个位置进行取反，需执行k次取反操作，可以多次选择同一个下标i，基于此操作返回数据可能的最大和
     * 贪心思路：如果数组元素中存在负数，则优先尽可能将负数转化为正数
     * - 优先转化最小的负数，如果数组中所有的负数转化后k还有剩余，则选择一个最小的正数进行一正一负抵消操作处理（剩余k为偶数直接抵消，剩余k为奇数则最小正数取反）
     */
    public int largestSumAfterKNegations(int[] nums, int k) {
        // ① 对数组元素进行排序
        Arrays.sort(nums);
        // ② 处理k次取反
        int sum = 0;
        int curMin = Integer.MAX_VALUE; // 维护最小值
        for (int i = 0; i < nums.length; i++) {
            // 如果为负数且k有剩余则执行取反
            if (nums[i] < 0 && k > 0) {
                nums[i] *= -1;
                k--;
            } else {
                // break; // 所有负数处理完成或者k不足了，则跳出处理
            }
            // 维护目前数组的最小值
            curMin = Math.min(curMin, nums[i]);
            // 遍历过程累加和
            sum += nums[i];
        }
        // ③ 校验剩余k
        if (k > 0) {
            if (k % 2 == 0) {
                return sum; // 剩余k为偶数，无论选择什么元素都是一正一负抵消，因此返回结果即为上述操作处理结果
            } else {
                // 选择目前数组的最小数取反
                return sum - 2 * curMin;
            }
        }
        // 返回结果
        return sum;
    }

}

👻方法2：最小堆（优先队列+k次取反+累加和）

思路分析

基于方法1贪心思路的分析，相当于每次都要取最小的元素（如果是负数且k>0则进行取反），因此可以构建一个最小堆维护数据的有序性，每次取出堆顶元素并取反后入队（k>0），当执行k次取反之后，读取目前堆中的值进行和累加

/**
 * 1005 K次取反后最大化的数组和
 */
public class Solution2 {

    // 最小堆
    public int largestSumAfterKNegations(int[] nums, int k) {

        // 构建最小堆
        PriorityQueue<Integer> queue = new PriorityQueue<>();
        for (int num : nums) {
            queue.offer(num);
        }

        // 取出堆顶元素(每次都拿最小的次数进行取反)
        while (k > 0) {
            int cur = queue.poll();
            cur *= -1;
            queue.offer(cur);
            // 取反完成
            k--;
        }

        // 依次弹出堆元素累加和
        int curMaxSum = 0; // 记录当前的最大数组和
        while (!queue.isEmpty()) {
            curMaxSum += queue.poll();
        }

        return curMaxSum;
    }

}

复杂度分析
- 时间复杂度：
- 空间复杂度：

🟢860-柠檬水找零

1.题目内容open in new window

在柠檬水摊上，每一杯柠檬水的售价为 5 美元。顾客排队购买你的产品，（按账单 bills 支付的顺序）一次购买一杯。

每位顾客只买一杯柠檬水，然后向你付 5 美元、10 美元或 20 美元。你必须给每个顾客正确找零，也就是说净交易是每位顾客向你支付 5 美元。

注意，一开始你手头没有任何零钱。

给你一个整数数组 bills ，其中 bills[i] 是第 i 位顾客付的账。如果你能给每位顾客正确找零，返回 true ，否则返回 false

2.题解思路

👻方法1：贪心算法（穷举法）

理解收银找零的方案：重点关心散纸的张数是否足够应付找零方案，不关心余额多少
- 客户给5 直接接收
- 客户给10 判断当前5的个数余量是否至少为1（找5）
- 客户给20 判断当前5的个数是否有3，或者是否满足5（至少1）、10（至少1）
  - 此处贪心思路的思考：此处20的找零方案有2种，一种是5+10，一种是3*5，此处应该尽可能保留5的纸币才能应对更多可能，因此此处优先选择5+10的方案处理，备选3*5
- 如果过程中不满足则说明没法找零，顺利遍历所有账单数据说明ok

/**
 * 860 柠檬水找零
 */
public class Solution1 {

    public boolean lemonadeChange(int[] bills) {
        // 初始化5 10 的零钱个数
        int fiveCnt = 0, tenCnt = 0;
        // 遍历账单信息判断是否足够找零
        for (int i = 0; i < bills.length; i++) {
            if (bills[i] == 5) {
                // 客户给了5,直接接收
                fiveCnt++;
            } else if (bills[i] == 10) {
                // 客户给了10，判断是否可以找零
                if (fiveCnt < 1) {
                    return false; // 5的张数不足，没法找零
                }
                // 满足找零条件，则更新余额
                tenCnt++;
                fiveCnt--;
            } else if (bills[i] == 20) {
                /**
                 * 贪心思路：此处20的找零方案有2种，一种是5+10，一种是3*5
                 * 此处应该尽可能保留5的纸币才能应对更多可能，因此此处优先选择5+10的方案处理，备选3*5
                 */
                // 客户给了10，判断是否可以找零
                if (fiveCnt >= 1 && tenCnt >= 1) { // 5和10至少有1张
                    // 满足找零条件，更新余额（选择方案）
                    fiveCnt--;
                    tenCnt--;
                } else if (fiveCnt >= 3) { // 5至少有3张
                    fiveCnt = fiveCnt - 3;
                } else {
                    return false; // 两种组合都不符合：5和10的张数都少于1，或者5的张数少于3
                }
            }

        }
        // 账单遍历完成
        return true;
    }
}

复杂度分析
- 时间复杂度：O（n）n 数组长度
- 空间复杂度：O（1）常量级别的占用

📯序列问题

🟡376-摆动序列

1.题目内容open in new window

如果连续数字之间的差严格地在正数和负数之间交替，则数字序列称为 **摆动序列。**第一个差（如果存在的话）可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。

例如， [1, 7, 4, 9, 2, 5] 是一个 摆动序列 ，因为差值 (6, -3, 5, -7, 3) 是正负交替出现的。
相反，[1, 4, 7, 2, 5] 和 [1, 7, 4, 5, 5] 不是摆动序列，第一个序列是因为它的前两个差值都是正数，第二个序列是因为它的最后一个差值为零。

子序列 可以通过从原始序列中删除一些（也可以不删除）元素来获得，剩下的元素保持其原始顺序。

给你一个整数数组 nums ，返回 nums 中作为 摆动序列 的 最长子序列的长度 。

示例 1：

输入：nums = [1,7,4,9,2,5]
输出：6
解释：整个序列均为摆动序列，各元素之间的差值为 (6, -3, 5, -7, 3) 。

示例 2：

输入：nums = [1,17,5,10,13,15,10,5,16,8]
输出：7
解释：这个序列包含几个长度为 7 摆动序列。
其中一个是 [1, 17, 10, 13, 10, 16, 8] ，各元素之间的差值为 (16, -7, 3, -3, 6, -8) 。

示例 3：

输入：nums = [1,2,3,4,5,6,7,8,9]
输出：2

2.题解思路

👻方法1：贪心（峰谷切换问题）

思路分析：先对特例进行判断，然后对其他情况进行讨论，实际上就是希望每次加入的元素能够使得序列构成小大小或者大小大的形式（也就是判断峰谷）让序列有更多的局部峰值
- 围绕x y z相邻三个元素差值分析，记录preDiff=y-x，在后续遍历的过程中去找这个z使其满足curDiff与preDiff相反（curDiff=z-y）满足条件则说明可以加入子序列并更新当前序列的上升下降趋势
- 代码要点分析：
  - 为什么preDiff=0的情况要计入判断，可以结合图示理解（是为了处理中间平坡的情况）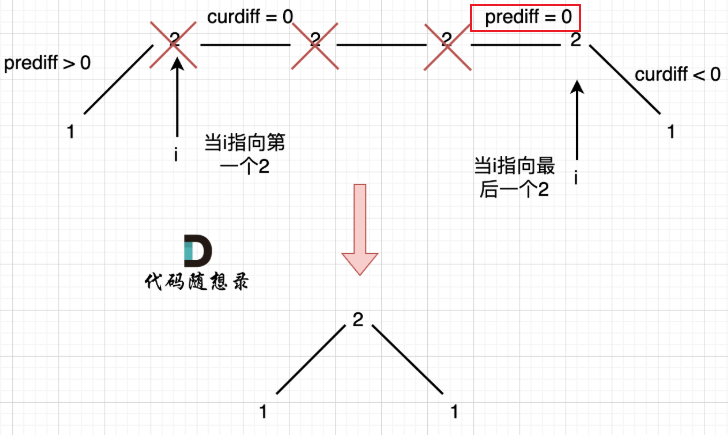

/**
 * 376 摆动序列
 */
public class Solution1 {
    // 返回nums中作为摆动序列的最长子序列长度
    public int wiggleMaxLength(int[] nums) {
        // 特例判断
        if (nums == null || nums.length == 0) {
            return 0;
        }
        if (nums.length == 1) {
            return 1;
        }
        if (nums.length == 2 && nums[0] != nums[1]) {
            return 2;
        }

        // 其余情况：峰 谷 选择（实际就是小大小或者大小大这种序列的选择，遇到相等差值就跳过）
        int preDiff = nums[1] - nums[0]; // 记录 x y z 相邻元素中的 x y 之间的差值
        int res = preDiff == 0 ? 1 : 2; // 初始化判断：如果差值为0则说明相等只能选1个元素，如果差值不为0则说明不相等可以构成上升或下降（即可以选2个元素）
        // 遍历剩余元素（依次加入剩余元素，判断是否可以构成小大小 或者 大小大 的情况）
        for (int i = 2; i < nums.length; i++) {
            // 获取当前元素与前一个元素的差值
            int curDiff = nums[i] - nums[i - 1];

            // 判断其【是否满足与前一个差值符号相反】的条件，如果满足则可以将这个元素加入到当前的摆动序列中
            if (preDiff <= 0 && curDiff > 0 || preDiff >= 0 && curDiff < 0) { // 判断当前序列的上升下降趋势 与 之前的是否相反
                res++; // 满足条件，加入该元素(出现了峰 或 谷)
                preDiff = curDiff; // 更新当前序列的上升|下降趋势
            }
        }
        // 返回结果
        return res;
    }
}

复杂度分析
- 时间复杂度：O(n)，其中 n 是序列的长度
- 空间复杂度：O(1)，只需要常数空间来存放若干变量

🟡053-最大子数组和

1.题目内容

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。子数组是数组中的一个连续部分。

2.题解思路

👻方法1：动态规划

思路分析：
- 【1】构建dp（dp[i]表示以当前数组元素结尾的最大连续子数组之和）
- 【2】初始化dp（dp[0]=nums[0]）
- 【3】状态转移方程：遍历每个元素，当前元素的最大子数组和有两个方面考虑细节：
  - nums[i] 能否带来正收益：如果nums[i] 能带来正收益就接上，如果不能带来正收益就断掉（断掉的话只能是nums[i]）
  - dp[i]必须以当前数组元素nums[i]结尾：要么基于前面的序列继续接上nums[i]，要么就在这里断开只取nums[i]（自称一派）
  - 基于上述分析得到状态转移方程dp[i] = max{dp[i-1]+nums[i],nums[i]}，随后获取到dp[]中的最大值
- 【4】构建dp并验证

/**
 * 最大子序和：最大连续子数组和
 */
class Solution1 {
    // 动态规划思路
    public int maxSubArray(int[] nums) {
        // 1.定义dp（dp[i] 表示以当前元素结尾的最大连续子数组和）
        int[] dp = new int[nums.length];

        // 2.初始化dp
        dp[0] = nums[0];

        // 3.状态转移方程:dp[i]=max{dp[i-1]+nums[i],nums[i]}

        // 4.构建dp
        for (int i = 1; i < nums.length; i++) {
            dp[i] = Math.max(dp[i - 1] + nums[i], nums[i]);
        }

        // 再次遍历构建好的dp数组，获取到max
        int maxVal = Integer.MIN_VALUE;
        for (int i = 0; i < dp.length; i++) {
            maxVal = Math.max(maxVal, dp[i]);
        }
        // 返回结果
        return maxVal;
    }
}

复杂度分析
- 时间复杂度：
- 空间复杂度：

动态规划（空间优化版本）

/**
 * 最大子序和：最大连续子数组和
 */
class Solution2 {
    /**
     * 动态规划思路: 空间优化版本
     * 1.dp[i]和dp[i-1]、nums[i] 有关
     * 2.可以在遍历的过程中就同步更新max的值
     * 基于此可以定义滚动变量来滚动存储，不需要记录整个dp数组
     */
    public int maxSubArray(int[] nums) {
        int maxVal = Integer.MIN_VALUE;
        int curMaxSum = 0;

        for (int i = 0; i < nums.length; i++) {
            curMaxSum = Math.max(curMaxSum + nums[i], nums[i]);
            maxVal = Math.max(maxVal, curMaxSum); // 在构建dp的时候同步更新maxVal
        }

        // 返回结果
        return maxVal;
    }
}

👻方法2：贪心算法

思路分析：不同于动态规划的思路，动态规划的分析点在于dp[i]的设计，判断当前元素是否可以接在当前的序列后面，如果可以就加上、不可以就自己作为一个新序列（其关注的是当前nums[i]可否给它带来正效益）；而贪心算法则是基于[负数+正数] 会变小的想法，其核心在于不让一个负数去加下一个数（即当连续和小于0的时候，则不加入下一个元素）
- 常见误区：如果仅仅基于贪心算法直接去写，容易先入一些边界条件的坑，需注意解题技巧
  - 先更新后判断：初始化从0开始计数，此处for对于第一个数先加入（数据元素本身就是一个子数组），然后更新maxVal，再去判断curSum是否小于等于0（负数），如果curSum为负数则砍断当前序列，下一个数从0开始累加

/**
 * 053 最大连续子数组和
 */
public class Solution1 {

    public int maxSubArray(int[] nums) {
        // 特例分析
        if (nums.length == 1) {
            return nums[0];
        }

        int maxVal = Integer.MIN_VALUE;
        int curSum = 0;

        for (int i = 0; i < nums.length; i++) {
            // 1.先更新
            curSum += nums[i];
            // 判断当前连续和是否为负数（如果为负数则不加入下一个数）
            maxVal = Math.max(maxVal, curSum); // 更新最大值（表示将当前元素加进来）

            // 2.后判断添加了这个元素之后如果连续子数组和变成负数的话，则下一个数开始从0开始计数（从次数开始断掉）
            if (curSum <= 0) {
                curSum = 0; // 重置（重新从下一个数开始计数）
            }
        }

        // 返回结果
        return maxVal;
    }

}

复杂度分析
- 时间复杂度：O（n） n 为数组长度
- 空间复杂度：O（1）占用常数级别的空间

🟡738-单调递增的数字

1.题目内容open in new window

当且仅当每个相邻位数上的数字 x 和 y 满足 x <= y 时，我们称这个整数是单调递增的。

给定一个整数 n ，返回小于或等于 n 的最大数字，且数字呈 单调递增 。

示例 1:

输入: n = 10
输出: 9

示例 2:

输入: n = 1234
输出: 1234

示例 3:

输入: n = 332
输出: 299

2.题解思路

👻方法1：贪心法

思路分析：
- 贪心核心：**"逆序"**找到非单调递增的位置，然后将这个位置idx+1开始后的数字都设置为9
  - 为什么要逆序而不是正序去找非单调递增的位置？
    - 以332为例，如果是正序处理的话，得到的结果是329，但显然这个并不是想要的答案，因为此时329并不是一个单调递增的数字序列
    - 继续以332为例，如果是逆序处理，322=>222 从后往前遍历才能重复利用上次比较的结果，随后处理当前位置idx+1之后的9（332->322->222->299）

/**
 * 738 单调递增的数字
 */
public class Solution1 {

    // 贪心：找到非单调递增的标记位
    public int monotoneIncreasingDigits(int n) {
        char[] nums = String.valueOf(n).toCharArray();
        // 逆序遍历每个数字,如果发现当前数字大于下一位数字,就将当前数字-1,记录这个位置
        int idx = -1;
        for (int i = nums.length - 2; i >= 0; i--) {
            if (nums[i] > nums[i + 1]) {
                nums[i]--;
                idx = i; // 记录这个位置
            }
        }

        // 如果idx存在，则将当前位置后面的所有位数设为9
        if (idx != -1) {
            for (int i = idx + 1; i < nums.length; i++) {
                nums[i] = '9';
            }
        }

        // 返回结果
        return Integer.valueOf(String.valueOf(nums));
    }

}

复杂度分析
- 时间复杂度：O（n）遍历数字字符序列
- 空间复杂度：构建辅助的字符数组进行处理

📯股票问题

买卖股票的最佳时机：低买高卖
买卖股票的最佳时机II：做T利润累加

🟢121-买卖股票的最佳时机

1.题目内容open in new window

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。

你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。

返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0

2.题解思路

👻方法1：贪心算法

思路分析：低买高卖（在可以卖出股票的日内，计算自己如果当日卖出股票（高卖）且是历史最低点买入股票（低买）是可以获得的利益，然后取得最大利益）
- 此处贪心的思路核心在于：每天都假设自己当日卖出股票，且是在当日之前以最低点买入的话所能获得的利益，计算出每个利润然后取最大（可以看到此处有两个"最值"概念，通过遍历数组得到，一个是该股票往期的最低点，一个是目前可获得利润的高大值)
  - 局部最优：日内可以获得得到最大利润（当日卖出股票-历史最低点）
  - 全局最优：从【每日最大利润的集合】中选取一个最大值，则可由局部最优 =》全局最优

/**
 * 121 买卖股票的最佳时机
 */
public class Solution1 {

    /**
     * 思路：贪心算法（低买高卖）
     * 核心：
     * 1.假设自己当日卖出股票，且该股票是在历史最低点买入的情况下所获得的利润差（局部最优）；
     * 2.计算每天基于【假设】所能得到的最大利润（由局部最优->全局最优）
     */
    public int maxProfit(int[] prices) {
        int minHistoryPrice = prices[0]; // 股票的历史最低点(以第1日开始)
        int maxProfit = 0; // 最大利润

        // 遍历（股票需隔日卖出，因此是从第2日开始计算利润）
        for (int i = 1; i < prices.length; i++) {
            // 计算当前利润
            int profit = prices[i] - minHistoryPrice; // 当日卖出价格-历史最低点=当日所得最大利润
            maxProfit = Math.max(maxProfit, profit); // 更新最大利润
            // 更新历史最低点
            minHistoryPrice = Math.min(minHistoryPrice, prices[i]);
        }

        // 返回最大利润
        return maxProfit;
    }
}

复杂度分析
- 时间复杂度：O（n）n 为价格列表长度
- 空间复杂度：O（1）占用常数级别的空间

🟡122-买卖股票的最佳时机II

1.题目内容open in new window

给你一个整数数组 prices ，其中 prices[i] 表示某支股票第 i 天的价格。

在每一天，你可以决定是否购买和/或出售股票。你在任何时候最多只能持有一股股票。你也可以先购买，然后在 同一天 出售。

返回 你能获得的最大利润

示例 1：

输入：prices = [7,1,5,3,6,4]
输出：7
解释：在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4。
随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6 - 3 = 3。
最大总利润为 4 + 3 = 7 。

示例 2：

输入：prices = [1,2,3,4,5]
输出：4
解释：在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4。
最大总利润为 4 。

示例 3：

输入：prices = [7,6,4,3,1]
输出：0
解释：在这种情况下, 交易无法获得正利润，所以不参与交易可以获得最大利润，最大利润为 0。

2.题解思路

👻方法1：贪心算法

思路分析：做T（nums[2]-nums[0]=(nums[2]-nums[1]) + (nums[1]-nums[0])），计算每天做T的利润差，如果利润>0就做，否则不动
- 局部最优：nums[2]-nums[0]=(nums[2]-nums[1]) + (nums[1]-nums[0]) 计算每日做T的利润差，正则累加，负则继续持有
- 全局最优：每日做T的正利润累加就是最大利润值
- ==误区：==此处一开始没想明白的话可能容易陷入到"怎么买？怎么卖？哪一天买？哪一天卖？"的问题导致思路混淆。但实际上可以不把关注点放在当日（因为日内买入卖出没有意义），而是两天为一个周期进行判断（今天卖的是昨天买的份额：nums[2]-nums[0]=(nums[2]-nums[1]) + (nums[1]-nums[0])，把每日做T的利润差拿到手即可）只收集正利润的区间（股票买卖的区间），而不记录区间

/**
 * 122 买卖股票的最佳时机II
 */
public class Solution1 {

    /**
     *  每日可操作股票，但最多只能持有一股
     */
    public int maxProfit(int[] prices) {
        /**
         * 贪心思路：收集正利润，如果有利润就做T，没利润就不动
         * nums[2]-nums[0] = (nums[2]-nums[1]) + (nums[1]-nums[0])
         * 即可以理解为假设每天做T能得到正利润，那么就去做，如果不能则继续持有等待，进而使得这个数值最大
         */
        int maxProfit = 0; // 初始化最大利润

        // 计算每日做T利润，如果存在正利润就累加，不存在正利润就继续持有
        for(int i=1;i<prices.length;i++){ // 第1天没有利润
            int curProfit = prices[i]-prices[i-1];
            if(curProfit>0){
                maxProfit += curProfit; // 累加正利润（做T）
            }
        }
        
        // 返回结果
        return maxProfit;
    }
}

复杂度分析
- 时间复杂度：O（n）n 为价格列表长度
- 空间复杂度：O（1）占用常数级别的空间

📯区间问题

🟡055-跳跃游戏

1.题目内容open in new window

给你一个非负整数数组 nums ，你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。

判断你是否能够到达最后一个下标，如果可以，返回 true ；否则，返回 false 。

示例 1：

输入：nums = [2,3,1,1,4]
输出：true
解释：可以先跳 1 步，从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。

示例 2：

输入：nums = [3,2,1,0,4]
输出：false
解释：无论怎样，总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 ， 所以永远不可能到达最后一个下标。

2.题解思路

👻方法1：贪心算法

贪心思路分析：在有效的覆盖范围内更新最大覆盖值（需注意跳跃不是油量累加概念，选择某个节点其可覆盖的范围是i=nums[i]）

以汽车加油为例，如果假设有n个加油站（nums表示每个加油站可以加的油量），判断汽车是否可以从起点走到终点。那么最贪心的思路就是，从第一个加油站出发（加满油），然后每到1个加油站就继续加满油上路，加满油后判断能够到达下一个加油站，可以就继续走，不行就返回false（直到油量大于总路程或者遍历结束，此时说明可以到达终点）

/**
 * 055 跳跃游戏
 */
public class Solution1 {
    // 贪心误区：此处是跳跃概念，并不是每到一个点都能够"加油"
    public boolean canJump(int[] nums) {
        // 定义当前位置可到达的最远位置
        int maxStep = 0;

        // 遍历每个节点：加油，并判断当前加油可否到达下一个节点
        for (int i = 0; i < nums.length; i++) {
            // 加油：更新当前可到达的最远位置
            maxStep += nums[i];

            if (maxStep < i + 1) {
                // 如果当前可到达的最远位置无法到达下一个加油站，则更加不可能往后走
                return false;
            }

            // 提前终止（如果当前加油量超过总里程，则必然可以到达终点，提前剪枝）
            if (maxStep >= nums.length-1) {
                return true;
            }
        }

        // 整个遍历完成，说明可以到达终点
        return true;
    }
}

但是上面的思路太贪心了，它是理想化情况下每次都能去每个加油站去加油，但实际上对于跳跃游戏来说，应该是在目前可以到达的加油站范围内的加油站才可以提供支持。例如加油加了3公里，那么只能是3公里范围内的加油站才可以提供支持；且对于跳跃游戏来说它并不是一直累加油量，而是选择选了某个节点之后只能用当前加油站提供的油量继续往下走

此处可以将题意抽象为始终有一个右边界maxCover，在遍历的过程中，应该在[0,maxCover]的有效范围内的加油站才可以提供支持。即遍历范围内的每个节点，在覆盖范围内更新更大的覆盖范围

/**
 * 055 跳跃游戏
 */
public class Solution3 {

    /**
     * 范围覆盖
     */
    public boolean canJump(int[] nums) {
        if (nums.length == 1) {
            return true;
        }

        // 定义覆盖范围
        int maxCover = 0;

        // 遍历每个节点：在覆盖范围内更新更大的覆盖范围
        for (int i = 0; i <= maxCover; i++) {
            // 在有效的覆盖范围内更新更大的覆盖范围
            maxCover = Math.max(maxCover, i + nums[i]);
            // 如果遍历过程中发现覆盖范围大于终点坐标，说明是可达终点的（此处在遍历过程中进行判断，不需要等到最后）
            if (maxCover >= nums.length - 1) { // 如果最大覆盖距离可到达最后一个位置则直接跳出（也是为了避免i在循环中取到maxCover导致越界）
                return true;
            }
        }

        // 其余情况
        return false;
    }
}

复杂度分析
- 时间复杂度：O（n）n 为数组长度
- 空间复杂度：O（1）占用常数级别

public boolean canJump(int[] nums) {
    int max = 0; // 此前可支撑的最大里程
    for(int i=0;i<nums.length;i++){
        // 判断当前的最大里程是否可以支持走到当前节点
        if(max<i){
            return false; // 无法走到当前节点
        }
        // 更新最大的覆盖范围（此处并不是简单的max+=nums[i]） 跳跃游戏不是油量累加，每一跳只依赖于当前nums[i]，其可覆盖的范围是i+nums[i]
        max = Math.max(max, i + nums[i]);
    }
    return true;
}

🟡045-跳跃游戏II

1.题目内容open in new window

给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。

每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说，如果你在 nums[i] 处，你可以跳转到任意 nums[i + j] 处:

0 <= j <= nums[i]
i + j < n

返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。

示例 1:

输入: nums = [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
     从下标为 0 跳到下标为 1 的位置，跳 1 步，然后跳 3 步到达数组的最后一个位置。

示例 2:

输入: nums = [2,3,0,1,4]
输出: 2

2.题解思路

👻方法1：贪心算法

结合题目分析，题目生成的测试用例可以到达nums[n-1]，则说明只需要关心怎么跳能以最小跳跃次数最快到达终点（这个时候就不要纠结能不能到达终点的问题）。此时只需要每次都跳到目前有效覆盖范围内可以达到的最远的那个位置即可

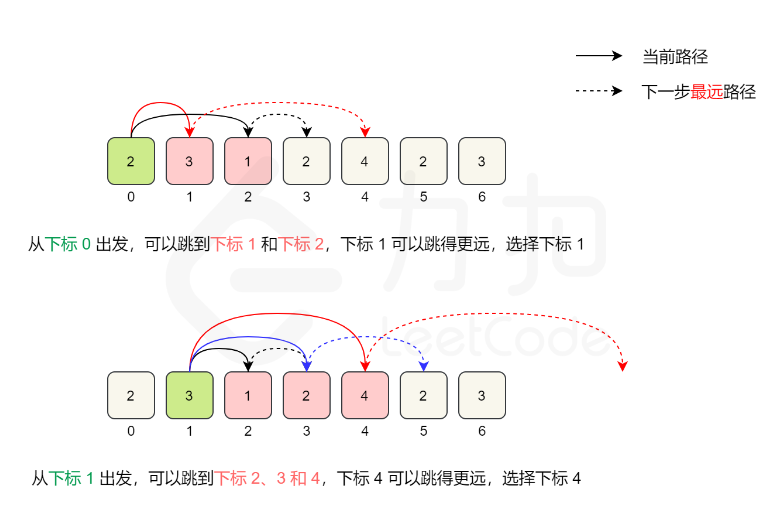
为什么i<nums.length - 1?：因为在访问最后一个元素之前，边界一定大于等于最后一个位置，否则就无法跳到最后一个位置。如果访问最后一个元素，在边界正好为最后一个位置的情况下，会增加一次「不必要的跳跃次数」，因此遍历不必访问最后一个元素

核心说明：
- 字段：maxCover当前位置可覆盖的最大跳跃位置、jumpPpinter上一跳指定的最大位置、cnt跳跃次数
- 遍历的过程中不断更新有效的覆盖范围maxCover，当走到上一跳指定的最大位置时i==jumpPpinter则进行跳跃并更新jumpPpinter作为下一个跳跃的目标位置

public class Solution1 {
    /**
     * 以最少的次数跳到终点（nums用例可以支持跳到终点）
     */
    public int jump(int[] nums) {
        int maxCover = 0; // 最大覆盖范围(当前位置i可跳的最大位置)
        int jumpPointer = 0; // 上一跳指定的可跳的最大位置 preStepMaxTarget
        int cnt = 0; // 跳跃次数

        for (int i = 0; i < nums.length - 1; i++) { // 此处遍历不必访问最后一个元素（考虑边界跳的情况）
            // 遍历过程中不断更新有效的覆盖范围
            maxCover = Math.max(maxCover, i + nums[i]);

            // 每次都选上一步可达到的最远的位置跳
            if (i == jumpPointer) {
                cnt++; // 跳
                jumpPointer = maxCover; // 当前可覆盖的最大范围作为下一个跳跃目标位置
            }
        }

        // 返回结果
        return cnt;
    }
}

复杂度分析
- 时间复杂度：O（n）n 为数组长度
- 空间复杂度：O（1）占用常数级别

🟡452-用最少数量的箭引爆气球

1.题目内容open in new window

有一些球形气球贴在一堵用 XY 平面表示的墙面上。墙面上的气球记录在整数数组 points ，其中 points[i] = [x_start, x_end] 表示水平直径在 x_start 和x_end之间的气球。你不知道气球的确切 y 坐标。

一支弓箭可以沿着 x 轴从不同点 完全垂直 地射出。在坐标 x 处射出一支箭，若有一个气球的直径的开始和结束坐标为 x_start,x_end，且满足 x_start ≤ x ≤ x_end，则该气球会被引爆。可以射出的弓箭的数量 没有限制 。弓箭一旦被射出之后，可以无限地前进。

给你一个数组 points ，返回引爆所有气球所必须射出的最小弓箭数 。

示例 1：

输入：points = [[10,16],[2,8],[1,6],[7,12]]
输出：2
解释：气球可以用2支箭来爆破:
-在x = 6处射出箭，击破气球[2,8]和[1,6]。
-在x = 11处发射箭，击破气球[10,16]和[7,12]。

示例 2：

输入：points = [[1,2],[3,4],[5,6],[7,8]]
输出：4
解释：每个气球需要射出一支箭，总共需要4支箭。

示例 3：

输入：points = [[1,2],[2,3],[3,4],[4,5]]
输出：2
解释：气球可以用2支箭来爆破:
- 在x = 2处发射箭，击破气球[1,2]和[2,3]。
- 在x = 4处射出箭，击破气球[3,4]和[4,5]。

2.题解思路

👻方法1：右边界排序 + 右端点射击

思路分析：右边界排序+右端点射击（按照右边界对区间进行排序，选择区间右端点进行射击（如果已覆盖的范围则不重复射击））
- 排序：基于Arrays.sort自定义排序规则，或者基于优先队列进行排序
步骤分析：[[10,16],[2,8],[1,6],[7,12]]
- （1）按照右边界对区间进行从小到大的排序[[1,6],[2,8],[7,12],[10,16]]
- （2）初始化第一个射击位置（选择第1个区间的右端点6）,随后依次遍历后面的节点，判断上一个射击点是否覆盖了该区间，如果覆盖则跳过，如果没有覆盖则选择新的射击点
  - 遍历[2,8]：其在上一个射击点6的覆盖范围内，无需重复射击
  - 遍历[7,12]：其不在上一个射击点6的覆盖范围内，选择新的射击点12（即当前区间的右端点）
  - 遍历[10,16]：其在上一个射击点12的覆盖范围内，无需重复射击
  - 遍历完成，可以看到只选择了两个射击点6 12即可完成所有气球的引爆
要点分析：此处因为边界触点也属于覆盖范围，所以下述两种验证方式都可行
- 此处是先初始化一个射击点，然后依次遍历所有区间，然后根据上一个射击点的位置和当前区间的关系决定是否要选择新的射击点
  - 思路1（校验覆盖范围）：如果上一个射击点在当前区间覆盖范围内（left<=shotIdx<=right），则不需要重复射击，继续遍历下一个区间
  - 思路2（只校验左边界）：如果上一个射击点不在当前区间覆盖范围内（shotIdx<left（因为对于区间来说right>=left始终成立，且基于前面的排序中shotIdx<=right也是始终成立的，因此此处如果shotIdx<left则说明上一个射击点和当前区间没有交集）），因此要选择一个新的射击点（即当前未覆盖区间的右端点作为新的射击点），然后更新射击点位置

/**
 * 452 用最少数量的箭引爆气球
 */
public class Solution1 {

    // 思路：右区间排序 + 右端点射击
    public int findMinArrowShots(int[][] points) {
        // 根据右区间排序
        Arrays.sort(points, new Comparator<int[]>() {
            @Override
            public int compare(int[] o1, int[] o2) {
                return o1[1] - o2[1];
            }
        });

        // 遍历区间
        int shotIdx = points[0][1]; // 初始化第一个射击点
        int cnt = 1; // 定义射击次数
        int m = points.length;
        for (int i = 0; i < m; i++) {
            // 遍历区间，如果区间在上一个射击范围内则跳过
            if (points[i][0] <= shotIdx && shotIdx <= points[i][1]) {
                continue;
            }
            // 如果当前区间没有在覆盖范围内，则选择其右边界作为射击点
            shotIdx = points[i][1];
            cnt++;
        }

        // 返回结果
        return cnt;
    }
}

复杂度分析
- 时间复杂度：二维数组排序 + 区间遍历
- 空间复杂度：常数级别空间占用

/**
 * 🟡 452 用最少数量的箭引爆气球 - https://leetcode.cn/problems/minimum-number-of-arrows-to-burst-balloons/description/
 */
public class Solution452_01 {

    /**
     * 贪心思路分析：将区间按照区间的右端点进行排序，然后每次选择一个右端点作为可能的射击点
     */
    public int findMinArrowShots(int[][] points) {
        int m = points.length, n = points[0].length;
        // 基于优先队列对数据进行排序
        PriorityQueue<int[]> pq = new PriorityQueue<>(new Comparator<int[]>() {
            @Override
            public int compare(int[] o1, int[] o2) {
                return (o1[1] != o2[1]) ? o1[1] - o2[1] : o1[0] - o2[0]; // 优先按照右端点排序
            }
        });
        // 初始化优先队列
        for (int i = 0; i < m; i++) {
            pq.add(points[i]);
        }

        // 基于上述排序选择可能的射击点（区间右端点可作为射击点参考）
        int shotIdx = pq.poll()[1]; // 初始化选择第1个区间的右端点为射击点
        int cnt = 1;
        // 遍历剩余数据，校验当前射击点是否覆盖了该数据，如果没有覆盖则需要选择新的射击点
        while (!pq.isEmpty()) {
            int[] cur = pq.poll();
            if (shotIdx >= cur[0] && shotIdx <= cur[1]) {
                // 满足覆盖位置，跳过
                continue;
            } else {
                // 选择新的射击位置
                shotIdx = cur[1];
                cnt++;
            }
        }
        // 返回结果
        return cnt;
    }
}

🟡435-无重叠区间（同【452】，m-cnt 概念）

1.题目内容open in new window

给定一个区间的集合 intervals ，其中 intervals[i] = [starti, endi] 。返回 需要移除区间的最小数量，使剩余区间互不重叠 。

注意只在一点上接触的区间是 不重叠的。例如 [1, 2] 和 [2, 3] 是不重叠的。

示例 1:

输入: intervals = [[1,2],[2,3],[3,4],[1,3]]
输出: 1
解释: 移除 [1,3] 后，剩下的区间没有重叠。

示例 2:

输入: intervals = [ [1,2], [1,2], [1,2] ]
输出: 2
解释: 你需要移除两个 [1,2] 来使剩下的区间没有重叠。

示例 3:

输入: intervals = [ [1,2], [2,3] ]
输出: 0
解释: 你不需要移除任何区间，因为它们已经是无重叠的了。

2.题解思路

👻方法1：贪心算法（右边界排序+右端点射击+注意边界处理）

核心：可参考【452-引爆气球】的思路，注意边界处理（触点不计入覆盖范围），结果用总区间数减去射击数即可（因为最少射击数表示了区间重复的分类情况，那么对于每种情况只需要保留1个区间即可，所以要移除的区间为m-cnt）

思路分析：本题和【452-用最少数量的箭引爆气球】的题型思路大同小异，但需注意边界处理和返回结果。【452】中求的是最少射击箭数（可以理解为此处保留的区间个数统计），那么【435】中返回的结果应该是m-cnt得到移除区间的最小数量
- 边界处理：【452】中判断射击位置是否被区间覆盖时包括了临界值（即只要射击位置触到了临界值也认为是覆盖到了），但此处针对边界的处理是点触区间不重复的概念，边界验证用shotIdx<=left更为简便（如果单纯只是用【452】中的第1种范围覆盖判断，则需要考虑边界条件）

/**
 * 435 无重叠区间
 */
public class Solution1 {

    public int eraseOverlapIntervals(int[][] intervals) {

        // 1.根据右区间排序
        Arrays.sort(intervals, new Comparator<int[]>() {
            @Override
            public int compare(int[] o1, int[] o2) {
                return o1[1] - o2[1];
            }
        });

        // 2.遍历区间
        int rightIdx = intervals[0][1]; // 初始化第一个右端点
        int cnt = 1; // 记录可保留的区间个数（可以理解为射箭数）
        int m = intervals.length;

        for (int i = 0; i < m; i++) {
            // 遍历区间，如果区间不上一个右端点的覆盖范围内（单点接触视为不重叠）则需进行标记（射出一箭）
            if (rightIdx <= intervals[i][0]) { // 如果上一个右边界位置位于当前比较区间边界的情况视作不覆盖
                cnt++;
                rightIdx = intervals[i][1];
            }
        }

        // 返回结果（需要删除的区间的最小数量为总区间数量减去需要保留的区间数量）
        return m - cnt;
    }
}

复杂度分析
- 时间复杂度：
- 空间复杂度：

/**
 * 🟡 435 无重叠区间 - https://leetcode.cn/problems/non-overlapping-intervals/description/
 */
public class Solution435_01 {

    /**
     * 思路转化：m-cnt 概念，cnt最小射击数量
     */
    public int eraseOverlapIntervals(int[][] intervals) {
        // ① 基于右端点进行排序
        Arrays.sort(intervals, new Comparator<int[]>() {
            @Override
            public int compare(int[] o1, int[] o2) {
                return o1[1] == o2[1] ? o1[0] - o2[0] : o1[1] - o2[1];
            }
        });

        // ② 寻找射击点,统计最少射击次数
        int shotIdx = intervals[0][1]; // 第一个区间的右端点作为射击点
        int cnt = 1; // 初始化弓箭数
        for (int i = 1; i < intervals.length; i++) {
            // 校验射击点是否覆盖区间，点接触不算覆盖
            if (shotIdx <= intervals[i][0]) {
                // 未覆盖区间，寻找新的射击点
                shotIdx = intervals[i][1];
                cnt++;
            }
            /*
            // 区间覆盖范围的校验条件控制
            if (shotIdx > intervals[i][0] && shotIdx <= intervals[i][1]) {
                continue;
            } else {
                // 未覆盖区间，寻找新的射击点
                shotIdx = intervals[i][1];
                cnt++;
            }
             */
        }

        // ③ 返回结果
        return intervals.length - cnt;
    }
}

🟡763-划分字母区间

1.题目内容open in new window

给你一个字符串 s 。我们要把这个字符串划分为尽可能多的片段，同一字母最多出现在一个片段中。

注意，划分结果需要满足：将所有划分结果按顺序连接，得到的字符串仍然是 s 。

返回一个表示每个字符串片段的长度的列表。

示例 1：

输入：s = "ababcbacadefegdehijhklij"
输出：[9,7,8]
解释：
划分结果为 "ababcbaca"、"defegde"、"hijhklij" 。
每个字母最多出现在一个片段中。
像 "ababcbacadefegde", "hijhklij" 这样的划分是错误的，因为划分的片段数较少。

示例 2：

输入：s = "eccbbbbdec"
输出：[10]

2.题解思路

👻方法1：遍历分割（两次遍历）

思路分析：通过字符出现最远距离取并集的方法，把出现过的字符都圈到一个区间里
- 关注【每个字母最多出现在一个片段中】这个切割条件，可以得到下述两个要点
  - （1）可能的切割位置：需要确定一个字母最后一个出现的位置（只有这个位置才有可能出现分割点）
  - （2）实际的切割位置：再次遍历字符串，遍历的同时更新当前已出现字符的最远出现位置下标maxIdx，如果这个maxIdx与当前遍历位置相等，作为切割位置
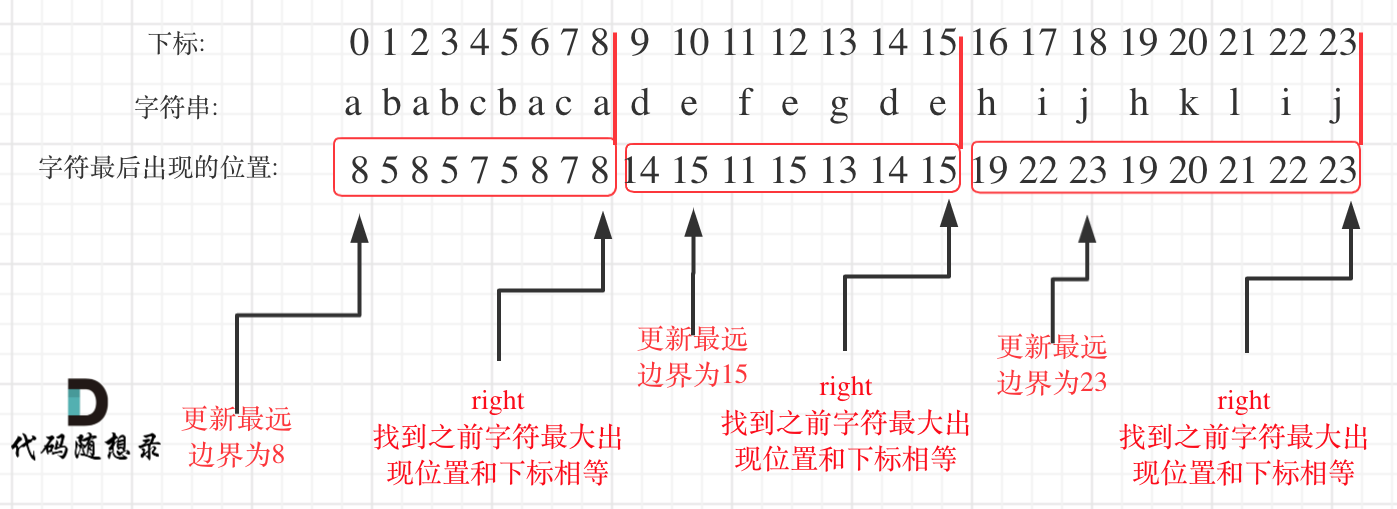
- 步骤分析：
  - （1）统计每个字母最后出现的位置
  - （2）再次遍历字符串，同步更新当前已出现字符的最远出现位置下标maxIdx，如果这个maxIdx与当前遍历位置相等，作为切割位置（同步记录结果：此处记录的是分段的长度，因此还需记录上一次的切割点）
    - 此处需注意maxIdx（可以理解为下一个切割位置，在遍历的过程中不断更新）、preCutIdx（上一个切割位置）的初始化值（边界处理）

/**
 * 763 划分字母区间
 */
public class Solution1 {

    /**
     * 核心条件：同一个字母最多只能出现在一个片段中
     * 1.第1次遍历：记录字母的最远出现位置（可能的切割点）
     * 2.第2次遍历：遍历字符串，同步更新当前【已出现字母的最远出现位置maxIdx】，如果当前遍历位置i与这个maxIdx相等，则此处即为切割点
     */
    public List<Integer> partitionLabels(String s) {
        // 1.存储每个字母最远出现位置
        Map<Character, Integer> map = new HashMap<>();
        for (int i = 0; i < s.length(); i++) {
            map.put(s.charAt(i), i);
        }

        // 2.遍历字符串，同步更新当前【已出现字母的最远出现位置maxIdx】，如果当前遍历位置i与这个maxIdx相等，则此处即为切割点
        int maxIdx = 0; // 已出现字母的最远出现位置maxIdx （此处只需要记录最远位置，因此不用额外的集合空间记录已出现的字符）
        int preCutIdx = -1; // 定义上一个切割索引位置（用于计算切割段长度）
        List<Integer> res = new ArrayList<>(); // 定义切割点结果集合
        for (int i = 0; i < s.length(); i++) {
            // 更新maxIdx、preCutIdx
            maxIdx = Math.max(maxIdx, map.get(s.charAt(i)));
            // 判断maxIdx是否与当前i相等，如果相等则记录切割位置
            if (i == maxIdx) {
                // res.add(i); // 此处i为切割位置，实际存储应为切割长度
                res.add(i - preCutIdx);
                preCutIdx = i; // 记录切割位置
            }
        }

        // 返回结果
        return res;
    }
}

复杂度分析
- 时间复杂度：O（n）n为字符串长度，此处需要遍历两次字符串
- 空间复杂度：O（n）需借助辅助集合存储每个字符的最远出现位置，以及其他常量级空间用于遍历存储切割点位置

另一种写法：思路调调差不多，只不多此处preCutIdx的概念被替换为startIdx(切割区间的开始位置，在每次执行切割操作后进行更新)；maxIdx即表示为下一个切割位置curIdx

startIdx：切割区间的开始位置，在每次执行切割操作后进行更新，会被更新为i+1(也就是curIdx+1,当前切割位置的下一位)
同理，那么此处切割长度应该为i-startIdx+1
且此处需注意起始值的初始化位置、以及curIdx的校验

/**
 * 🟡763 划分字母区间 - https://leetcode.cn/problems/partition-labels/
 */
public class Solution763_02 {

    /**
     * 思路分析：关注【每个字母最多出现在一个片段中】这个切割条件
     * - ① 可能的切割位置：每个字母的最后一次出现的位置
     * - ② 实际的切割位置：已出现的字母序列中的最后一次出现的位置的最大值，当遍历到这个位置可以进行切割（可以确保字母只在当前片段中出现）
     */
    public List<Integer> partitionLabels(String s) {
        // 第1次遍历：统计每个字母字符的最后一次的出现位置
        Map<Character, Integer> map = new HashMap<>();
        for (int i = 0; i < s.length(); i++) {
            map.put(s.charAt(i), i);
        }

        List<Integer> res = new ArrayList<>();

        // 第2次遍历：寻找实际的切割位置
        int cutIdx = 0; // 存储已出现的字母序列中最后一次出现的位置的最大值（切割位置会随着遍历元素的出现不断更新）
        int startIdx = 0; // 记录当前切割的起始点，用于划分切割区域（每次切割后进行更新）
        for (int i = 0; i < s.length(); i++) {
            // 更新已出现的字母的出现位置的最大值
            cutIdx = Math.max(cutIdx, map.get(s.charAt(i)));
            if (i == cutIdx) {
                // 如果遍历到当前的最大切割位置，则进行切割操作
                res.add(i - startIdx + 1);
                startIdx = i + 1; // 选择切割，更新下一个切割范围的起始点
            }
        }

        // 返回结果
        return res;
    }
}

🟡056-合并区间

1.题目内容open in new window

以数组 intervals 表示若干个区间的集合，其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间，并返回 一个不重叠的区间数组，该数组需恰好覆盖输入中的所有区间 。

示例 1：

输入：intervals = [[1,3],[2,6],[8,10],[15,18]]
输出：[[1,6],[8,10],[15,18]]
解释：区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].

示例 2：

输入：intervals = [[1,4],[4,5]]
输出：[[1,5]]
解释：区间 [1,4] 和 [4,5] 可被视为重叠区间。

2.题解思路

👻方法1：排序+遍历合并（贪心思路）

思路分析：

实现步骤：此处贪心的体现实际上就是固定左边界，不断去寻找可覆盖的最大右边界并更新（也可以就单纯理解为普通的合并思路，用了贪心而不自知）
- （1）排序：固定左边界，先按照区间左边界进行排序
- （2）遍历：循环遍历区间，根据区间右边界进行一一匹配合并

/**
 * 056 合并区间
 */
public class Solution1 {
    public int[][] merge(int[][] intervals) {

        // 1.对区间进行排序（按照左边界从小到大排序）
        Arrays.sort(intervals, new Comparator<int[]>() {
            @Override
            public int compare(int[] o1, int[] o2) {
                return o1[0] - o2[0];
            }
        });

        // 2.遍历区间一一进行合并
        List<int[]> res = new ArrayList<>(); // 定义结果集
        int curLeft = intervals[0][0], curRight = intervals[0][1]; // 初始化选择第1个区间作为合并目标
        for (int i = 1; i < intervals.length; i++) {
            /**
             * curRight 与 [left,right] 进行比较
             * curRight < left : 无重叠区间，需将当前区间加入结果集，并更新合并区间的最新状态
             * curRight >= left:
             *  - curRight < right: 合并后 需更新右边界
             *  - curRight >= right: 当前已完全覆盖，无需更新
             */
            int left = intervals[i][0], right = intervals[i][1];
            if (curRight < left) {
                res.add(new int[]{curLeft, curRight});
                curLeft = left;
                curRight = right;
            } else {
                if (curRight < right) {
                    curRight = right;
                }
            }
        }
        // 遍历完成，将当前的合并区间载入
        res.add(new int[]{curLeft, curRight});

        // 返回结果
        return res.toArray(new int[res.size()][]);

    }
}

复杂度分析
- 时间复杂度：排序O（nlogn）+遍历O（n）
- 空间复杂度：排序占用的空间复杂度（O(logN) java 的内置排序是快速排序需要 O(logN)空间）+遍历时占用常数级别空间（结果集不计的话）

📯两个维度权衡问题

🔴135-分发糖果

1.题目内容open in new window

n 个孩子站成一排。给你一个整数数组 ratings 表示每个孩子的评分。

你需要按照以下要求，给这些孩子分发糖果：

每个孩子至少分配到 1 个糖果。
相邻两个孩子评分更高的孩子会获得更多的糖果。

请你给每个孩子分发糖果，计算并返回需要准备的 最少糖果数目

2.题解思路

👻方法1：两次遍历（动态规划+贪心算法）

思路分析：将【相邻两个孩子评分更高的孩子会获得更多的糖果】拆分为左右规则进行校验，选择同时满足两个规则的糖果数（此处的思路有点类似【求左右乘积】的动态规划思路）
- 此处一开始可能会想着先对数组进行【从小到大】排序，然后按照顺序定义level，遇到评分增加（上升序列）则level+1（多发1个糖果），累加糖果数量（错误❌ 不能对其先排序）
- 两次遍历：将上述规则拆分为左规则、右规则（此处拆分的思路就是为了避免被左、右的因素干扰，导致不知道当前i的平衡点而思路混淆，两边同时讨论只会顾此失彼）
  - 左规则：当nums[i-1]<nums[i]时，i号学生的糖果数量将比i-1号孩子的糖果数量多一个
    - 贪心思路：i评分比i-1小或者相等，则最少只需要分1个（此处只考虑左规则，不要被右边的影响）
  - 右规则：当nums[i]>nums[i+1]时，i号学生的糖果数量将比i+1号孩子的糖果数量多一个
    - 贪心思路：i评分比i+1小或者相等，则最少只需要分1个（此处只考虑右规则，不要被左边的影响）
  - 分别遍历该数组两次，判断每个学生i如果分别满足左规则、右规则的情况下需要分得多少个糖果，要同时满足两个规则则需要选择两者较大的那个糖果数

/**
 * 135 分发糖果
 */
public class Solution2 {
    /**
     * 动态规划 + 贪心思路
     * 将校验规则分为两条：左、右规则，计算分别满足这两条规则的情况下需要多少个糖果，要同时满足两个规则则需要选择两者较大的那个糖果数
     */
    public int candy(int[] nums) { // int[] ratings
        int n = nums.length;
        // 左规则：如果nums[i-1]<nums[i]成立，则i号学生会比i-1号学生多一个糖果
        int[] left = new int[n];
        left[0] = 1; // 初始化左规则：left[i] 表示每个学生满足左规则条件下所需的最少糖果数
        for (int i = 1; i < n; i++) {
            // 如果i评分比i-1大则比它多1个糖果即可，如果比i-1评分小则取最小为1
            left[i] = (nums[i] > nums[i - 1]) ? left[i - 1] + 1 : 1;
        }

        // 右规则：如果nums[i]>nums[i+1] 表示i号学生会比i+1号学生多一个糖果（因此此处需要先确认nums[i+1]所需的最少糖果数量，采用逆向遍历的思路）
        int[] right = new int[n];
        right[n - 1] = 1; // 初始化右规则：right[i] 表示每个学生满足右规则条件下所需的最少糖果数
        for (int i = n - 2; i >= 0; i--) { // 逆序遍历
            // 如果i评分比i+1大则比它多1个糖果即可，如果比i+1评分小则取最小为1
            right[i] = (nums[i] > nums[i + 1]) ? right[i + 1] + 1 : 1;
        }

        // 左右规则汇聚（要同时满足左右规则，因此选则两者之间的最大值即可）
        int cnt = 0;
        for (int i = 0; i < n; i++) {
            cnt += Math.max(left[i], right[i]);
        }
        // 返回结果
        return cnt;
    }
}

复杂度分析
- 时间复杂度：O（n）上述思路需遍历3次数组
- 空间复杂度：O（n）需借助辅助数组进行构建

空间优化版本

分析上述的代码，实际上当得到left[]数组之后，对于right[]的求解不需要完整地存储right[]，而是在处理右规则的同时顺便就将结果给处理，这样可以节省内存空间

对于left[]：left[i]的取值依赖于left[i-1]（要先得到left[i-1]所以是正序遍历）
对于right[]：right[i]的取值依赖于right[i+1]（要先得到right[i+1]所以是逆序遍历）
- 空间优化：借助滚动变量记录right[i+1]，在处理right[]的过程中附带处理结果（注意数组的起点终点以及需要计算的位置（即下标索引））

/**
 * 135 分发糖果
 */
public class Solution3 {
    /**
     * 动态规划 + 贪心思路
     * 将校验规则分为两条：左、右规则，计算分别满足这两条规则的情况下需要多少个糖果，要同时满足两个规则则需要选择两者较大的那个糖果数
     * 空间优化版本：只需要保存left[],对于右规则的处理，可以在处理右规则的同时顺便处理相应的结果（这是动态规划空间优化的一种常见思路：此处i只依赖于i+1，因此只需要记录每次的i+1即可）
     */
    public int candy(int[] nums) { // int[] ratings
        int n = nums.length;
        int cnt = 0; // 糖果数量累加计数值

        // 左规则：如果nums[i-1]<nums[i]成立，则i号学生会比i-1号学生多一个糖果
        int[] left = new int[n];
        left[0] = 1; // 初始化左规则：left[i] 表示每个学生满足左规则条件下所需的最少糖果数
        for (int i = 1; i < n; i++) {
            // 如果i评分比i-1大则比它多1个糖果即可，如果比i-1评分小则取最小为1
            left[i] = (nums[i] > nums[i - 1]) ? left[i - 1] + 1 : 1;
        }


        // 右规则：如果nums[i]>nums[i+1] 表示i号学生会比i+1号学生多一个糖果（因此此处需要先确认nums[i+1]所需的最少糖果数量，采用逆向遍历的思路）
        int rightCandy = 1; // 初始化右规则：rightCandy始终指向i右边学生分配的最少糖果数
        for (int i = n - 1; i >= 0; i--) { // 逆序遍历(注意此时的起点和终点讨论)
            // 如果i评分比i+1大则比它多1个糖果即可，如果比i+1评分小则取最小为1
            int curCandy = 1;
            if (i < n - 1 && nums[i] > nums[i + 1]) {
                curCandy = rightCandy + 1; // 从n-2的位置才开始计算当前学生i满足有规则所需的最少糖果数
            }
            // 累加同时满足左右规则所需的糖果数
            cnt += Math.max(left[i], curCandy);
            // 更新rightCandy
            rightCandy = curCandy;
        }

        // 返回结果
        return cnt;
    }
}

👻方法2：常数空间优化

一次遍历版本优化参考

class Solution {
    public int candy(int[] ratings) {
        int n = ratings.length;
        int[] left = new int[n];
        for (int i = 0; i < n; i++) {
            if (i > 0 && ratings[i] > ratings[i - 1]) {
                left[i] = left[i - 1] + 1;
            } else {
                left[i] = 1;
            }
        }
        int right = 0, ret = 0;
        for (int i = n - 1; i >= 0; i--) {
            if (i < n - 1 && ratings[i] > ratings[i + 1]) {
                right++;
            } else {
                right = 1;
            }
            ret += Math.max(left[i], right);
        }
        return ret;
    }
}

🟡406-根据身高重建队列

1.题目内容open in new window

假设有打乱顺序的一群人站成一个队列，数组 people 表示队列中一些人的属性（不一定按顺序）。每个 people[i] = [hi, ki] 表示第 i 个人的身高为 hi ，前面正好有 ki 个身高大于或等于 hi 的人。

请你重新构造并返回输入数组 people 所表示的队列。返回的队列应该格式化为数组 queue ，其中 queue[j] = [hj, kj] 是队列中第 j 个人的属性（queue[0] 是排在队列前面的人）。

示例 1：

输入：people = [[7,0],[4,4],[7,1],[5,0],[6,1],[5,2]]
输出：[[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]]
解释：
编号为 0 的人身高为 5 ，没有身高更高或者相同的人排在他前面。
编号为 1 的人身高为 7 ，没有身高更高或者相同的人排在他前面。
编号为 2 的人身高为 5 ，有 2 个身高更高或者相同的人排在他前面，即编号为 0 和 1 的人。
编号为 3 的人身高为 6 ，有 1 个身高更高或者相同的人排在他前面，即编号为 1 的人。
编号为 4 的人身高为 4 ，有 4 个身高更高或者相同的人排在他前面，即编号为 0、1、2、3 的人。
编号为 5 的人身高为 7 ，有 1 个身高更高或者相同的人排在他前面，即编号为 1 的人。
因此 [[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]] 是重新构造后的队列。

示例 2：

输入：people = [[6,0],[5,0],[4,0],[3,2],[2,2],[1,4]]
输出：[[4,0],[5,0],[2,2],[3,2],[1,4],[6,0]]

2.题解思路

👻方法1：联合排序（先h后k）+ 遍历并按k插入

思路分析：本题涉及两个维度（h和k），遇到这种题型一定要控制变量（先确定一个维度，然后按照另一个维度排列），否则就会顾此失彼（参考135-分发糖果）
- 是先按照k排还是先按照h?：如果单纯按照k或者h排列的话，就会发现无论怎么排都无法不符合条件，两个维度都没有确定下来，因此考虑联合字段排序：先h后k（即按照h从大到小排序，对于h相同的按照k从小到大排序，以此保证了前面的节点身高一定比本节点高）
  - 局部最优：按照身高高的people的k来进行插入，可以保证身高顺序的同时，后面插入的节点又不会影响前面已经插入的节点
  - 全局最优：所有数据正常入队，整个队列满足队列属性
- ==处理结果集为什么选择List？==注意此处的关键字是插入，也就是说当明确了身高高低排序之后，需要根据前面排了几个比我高的人这个参数进行判断要插入到哪个位置，才不会影响现有的顺序规则。而这个插入操作则需要借助适合操作插入的数据结构来进行处理，而List的add(index,item)方法提供了可以直接将元素插入指定索引位置的方法。如果用数组去做的话，在插入的时候好还需要手动将这个插入位置及之后的所有元素后移，因此此处选用List更为合适，构建完成之后再将集合转为结果需要的二维数组即可
- 案例分析：[[7,0],[4,4],[7,1],[5,0],[6,1],[5,2]]
  - 联合排序（先h后k）：[[7,0] [7,1] [6,1] [5,0] [5,2] [4,4]]
    - 优先按照h从大到小进行排序
    - 如果h相同，则按照k从小到大进行排序
  - 依次选择元素入队：根据排序后的顺序，结合k进行处理，k 表示前面有几个比我高的元素，如果为2，那么插入位置就为2（因为前面的插入顺序已经确保了前面插入的节点肯定比当前节点身高要高，所以此处插入只需要根据k选择插入在第几个位置直接插入即可）

public int[][] reconstructQueue(int[][] people) {
    // 1.联合排序（先h后k：先按照身高从高到低排序，身高相同则按照k从小到大排序）
    Arrays.sort(people, (a, b) -> {
        if(a[0]==b[0]){
            return a[1]-b[1]; // 如果身高相同，按照k从小到大
        }else{
            return b[0]-a[0]; // 按照身高从高到低
        }
    });

    // 2.遍历排序后的数据，根据每个元素的k插入数据
    List<int[]> list = new ArrayList<>(); // 借助List构建插入顺序（int[]为对应的元素），选用List主要考虑便于插入操作
    for(int[] p : people){
        list.add(p[1],p); // add(index,item); 将元素插入指定索引位置（对照此处根据k插入元素）
    }
    return list.toArray(new int[people.length][]);
}

复杂度分析
- 时间复杂度：排序的时间复杂度 + 遍历二维数组的时间复杂度
- 空间复杂度：借助List构建结果集

给定两个整数数组 gas 和 cost ，如果你可以按顺序绕环路行驶一周，则返回出发时加油站的编号，否则返回 -1 。如果存在解，则保证它是唯一的。

示例 1:

输入: gas = [1,2,3,4,5], cost = [3,4,5,1,2]
输出: 3
解释:
从 3 号加油站(索引为 3 处)出发，可获得 4 升汽油。此时油箱有 = 0 + 4 = 4 升汽油
开往 4 号加油站，此时油箱有 4 - 1 + 5 = 8 升汽油
开往 0 号加油站，此时油箱有 8 - 2 + 1 = 7 升汽油
开往 1 号加油站，此时油箱有 7 - 3 + 2 = 6 升汽油
开往 2 号加油站，此时油箱有 6 - 4 + 3 = 5 升汽油
开往 3 号加油站，你需要消耗 5 升汽油，正好足够你返回到 3 号加油站。
因此，3 可为起始索引。

示例 2:

输入: gas = [2,3,4], cost = [3,4,3]
输出: -1
解释:
你不能从 0 号或 1 号加油站出发，因为没有足够的汽油可以让你行驶到下一个加油站。
我们从 2 号加油站出发，可以获得 4 升汽油。 此时油箱有 = 0 + 4 = 4 升汽油
开往 0 号加油站，此时油箱有 4 - 3 + 2 = 3 升汽油
开往 1 号加油站，此时油箱有 3 - 3 + 3 = 3 升汽油
你无法返回 2 号加油站，因为返程需要消耗 4 升汽油，但是你的油箱只有 3 升汽油。
因此，无论怎样，你都不可能绕环路行驶一周。

2.题解思路

👻方法1：贪心算法

核心思路：遍历数组，确认可行的加油站起点位置（中间不断油）+ 可以跑完一圈（遍历完所有加油站仍有油量剩余）
- 中间不断油：出现curGas<0说明断油，需要选择下一个加油站起点（重置起点startIdx和curGas）
- 判断是否可以跑完一圈：所有加油站遍历完成，如果tataoGas>0说明可以跑完一圈
思路分析：遍历以每个加油站为起点出发的情况，判断是否可以顺利走下去，如果无法走到下一个加油站，则需要以下一个加油站为起始点开始。
- 假设是在【1号加油站】出发，前进走到【2号加油站】进行验证如果当前可以到达下一个加油站（剩余油量刚好或者足够）则继续前进，如果其当前油量不足则说明其无法走到下一个加油站，那么说明以【1号加油站】这个起点开始出发的策略是走不通的（因为中间出现断油的情况）；
- 基于此分析局部最优的概念是判断当前加油站剩余油量是否可以走到下一个加油站，如果不行就以下一个加油站为起点出发；而全局最优的是基于局部最优，在这个过程中不断调整起点，最终如果可以遍历完所有的加油站且总油量大于等于0则找到可行的起始站，否则返回-1
- 步骤分析：
  - （1）初始化参数：起始站索引（startIdx）、从起始站出发的当前剩余油量（curGas）、总油量（totalGas）
  - （2）遍历每个加油站，更新curGas、totalGas（类似预先计算如果要走到下一个加油站后剩余油量和总油量有多少），然后判断当前油量是否可以支撑走到下一个加油站
    - 如果curGas>=0 说明可以走到下一个加油站
    - 如果curGas<0说明无法走到下一个加油站，只能从下一个加油站开始重新出发（curGas=0;startIdx=i+1）
      - ==为什么是只能？==假设从i->j则必须要求i->j之间的所有节点都是可达的（i->m->n->j），如果说中间存在m->n不可达，则说明以i为起点的这段路程走不下去，既然走不下去就只能从n重新开始（因为m->n也不可达，所以不会选m作为起点）
  - （3）当所有的加油站遍历完成，判断总油量是否大于等于0（如果满足totalGas>=0说明当前找的加油站起点是可以满足的，至于tataoGas>=0才能保证整个过程的供油量满足耗油量（跑完一圈），即有解）

/**
 * 134 加油站
 */
public class Solution1 {
    /**
     * 从某个加油站出发，可以绕所有加油站一圈
     */
    public int canCompleteCircuit(int[] gas, int[] cost) {
        int curGas = 0;   // 当前剩余油量
        int startIdx = 0; // 出发起点的加油站索引
        int totalGas = 0; // 走到某个节点的总油量

        int n = gas.length;
        for (int i = 0; i < n; i++) {
            // 到达某个加油站，进行加油，并判断当前油量是否可以支撑它走到下一个加油站
            totalGas = totalGas + (gas[i] - cost[i]); // 总油量
            curGas = curGas + (gas[i] - cost[i]); // 当前剩余油量
            if (curGas < 0) {
                // 如果当前剩余油量小于0，说明无法走到下一个加油站，则需从下一个加油站开始重新出发
                curGas = 0;
                startIdx = i + 1;
            }
        }
        // 遍历完成，判断最终的totalGas是否大于0
        return totalGas >= 0 ? startIdx : -1;
    }
}