难度说明：🟢简单🟡中等🔴困难

学习资料

• 代码随想录

学习目标

• 掌握数据结构核心基础
• 借助数据结构完成常见题型

skill-03-哈希表

理论基础

1.核心理论

​ 哈希表（英文名字为Hash table，国内也有一些算法书籍翻译为散列表），哈希表是根据关键码的值而直接进行访问的数据结构。

​ 例如数组可以理解为一张哈希表，通过数组的索引下标直接访问数组元素，一般哈希表用于快速判断一个元素是否出现在集合中

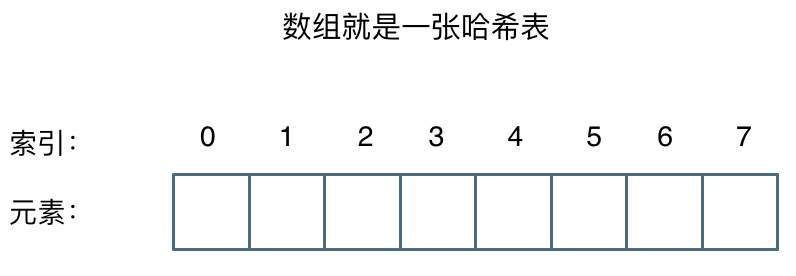
场景：哈希表用于快速判断一个元素是否出现在集合中

​ 例如要查询一个名字是否在这所学校里。直接通过枚举的话时间复杂度是O(n)，但如果使用哈希表的话只需要O(1)的时间复杂度。

​ 做法：在初始化的时候把这所学校里学生的名字都存在哈希表里，在查询的时候通过索引直接就可以知道这位同学在不在这所学校里了。将学生姓名映射到哈希表上就涉及到了hash function ，也就是哈希函数

（1）哈希函数

​ 哈希函数，把学生的姓名直接映射为哈希表上的索引，然后就可以通过查询索引下标快速知道这位同学是否在这所学校里

​ 通过hashCode把名字转化为数值，一般hashcode是通过特定编码方式，可以将其他数据格式转化为不同的数值，进而把学生名字映射为哈希表上的索引数字

​ 如果通过hashCode得到的数值大于哈希表的大小（tableSize），一般为了保证映射出来的索引数值都落在哈希表，则会再次对数值做一个取模的操作，以保证学生姓名一定可以落到哈希表上，但这个过程可能就会出现哈希碰撞问题（不同元素经过哈希计算之后得到相同的索引值，也就是映射到同一个索引下标位置，这种现象称为哈希碰撞）

（2）哈希碰撞

​ 例如图示小李和小王通过哈希计算都映射到了索引下标的位置，导致出现哈希碰撞。一般采用线性探测法和拉链法来解决

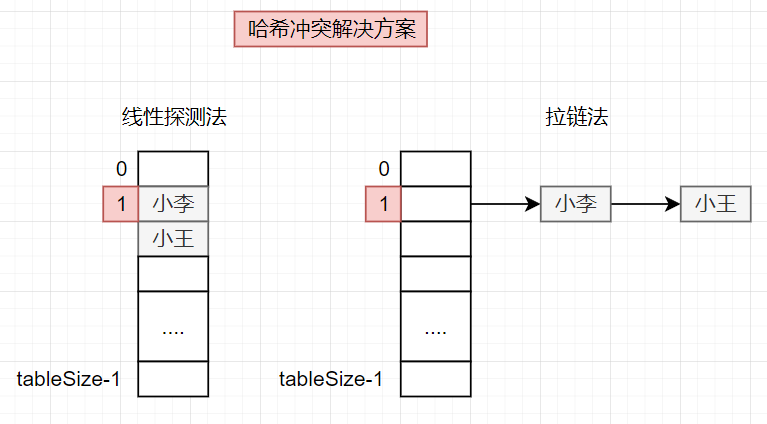
线性探测法

​ 如果当前索引位置存在冲突，则继续寻找下一个可用的位置，这种方式为了确保所有元素能够存放到哈希表中，则必须保证tableSize>dataSize，借助空位来解决碰撞问题

拉链法

​ 将发生冲突的元素存储到一条链表上，基于此区分冲突元素

​ 拉链法的选择要适当考虑哈希表的大小，避免因为数组空值而浪费大量内存，也避免因为链表太长而降低检索效率

（3）常见的3种哈希结构

当想使用哈希法来解决问题的时候，一般会选择如下三种数据结构

• 数组
• set （集合）
• map(映射)

2.技巧总结

​ 当遇到要快速判断元素是否出现在集合中的时候考虑用哈希法，但哈希法也是牺牲了空间换取时间（因为要用到额外的哈希结构（数组、set、map）来存放数据，以实现快速查找）

• 数组作为哈希表：例如有效的字母异位词、赎金信（题目限定了小写字母），因此可以选用限定固定大小的数组作为哈希表存储每个字符出现的次数（虽然也可以使用map存储，但map存储的空间消耗会比数组大一点，因为map要考虑维护红黑树或者符号表，还需做哈希函数的运算，不如数组简单直接）
  • 针对数组：因为数组的大小是有限的，针对一些限定场景可以优先考虑数组，但是如果一些集合大小不固定的场景，如果局限于开辟大数组空间的话就很容易导致空间性能浪费，那倒不如转变思路选用其他合适的哈希集合进行存储
• set作为哈希表：例如两个数组的交集、快乐数由于没有限定数值数量，因此无法用数组，而是选用set存储
• map作为哈希表：例如两数之和、四数之和II场景，既要判断两数之和是否满足target，又要返回满足条件的下标索引，因此可以选用map存储
  • 但是三数之和、四数之和这个场景中如果用哈希表可能稍显麻烦，而是选用排序+双指针的思路实现，因为它不需要考虑原下标索引（排序会打乱元素位置），因此只需要关注满足三元组、四元组的组合数
  • 而四数之和II是在不同的数组中取x+y+z+w=0的元素，不需要考虑重复问题

常见题型思路总结

• 242-有效的字母异位词

  • 【排序法】：判断排序后的字符序列是否完全一致
  • 【统计法】：判断每个字符的出现次数是否完全一致（可以一个统计、一个使用校验）

• 349-两个数组的交集

  • 【哈希法】：将数组1元素加入set，遍历数组2快速判断元素是否在set出现，如果出现则为交集加入结果集（需去重）

• 202-快乐数

  • 【哈希法】：数位分离（getNext） + 哈希判断（校验是否出现循环数）

• 001-两数之和

  • 【哈希法】：将数组元素加入map（需处理索引），快速判断target-x是否在map中出现，如果出现则满足两数之和

• 454-四数相加

  • 【拆分法】：x+y+u+v=0统计这样的组合个数
    • ① 两两拆分，分别计算(x,y)、(u,v)组合中每个元素组的两数之和的出现次数，构建为map1、map2
    • ② 遍历map1、map2统计两个集合中元素出现i+j=0的组合个数（组合个数应为满足元素对应出现次数的乘积，然后累加和统计）

• 383-赎金信

  • 【统计法】：基于magazine构建一个字符池map（存储字符及其出现次数），遍历ransomNote字符序列是否可以尤其构成（使用一个字符就取出，校验更新后的字符池会不会出现负数）

• 015-三数之和

  • 【暴力循环】：通过暴力循环嵌套
  • 【排序+双指针】：从一个整数数组nums中获取到满足x+y+z=0且不重复的三元组
    • ① 对nums进行排序（为了便于通过指针定位三元组）
    • ② 外层固定i，内层通过双指针分别从剩余的序列的头尾向中间靠拢寻找三元组(根据当前组合和决定指针更新方向)
      • 去重思路①：contains校验集合是否重复
      • 去重思路②：对于连续出现的x,y,z都可做去重排查处理
      • 在优化算法的时候结合题意处理一下特例情况，通过剪枝的方式提升算法效率：基于对[x,y,z]:x+y+z=0及数组有序的思考，通过剪枝来达到去重的效果

• 018-四数之和（与015-三数之和的思路类似，只不过此处是求[x,y,u,v]，同理也是通过固定元素的方式来实现）

  • 【暴力循环】：通过暴力循环嵌套
  • 【降维+排序+双指针】：从一个整数数组nums中获取到满足x+y+u+z=0且不重复的四元组
    • 所谓降维实际为四维降三维概念，通过固定x，然后将其转化为求[y,u,z]的三维形式（回归015的解题思路），在这个过程中注意剪枝处理即可。即基于每个x构成的满足[y,u,v](y+u+v=target-x的三元组) 构成的四元组
      • 第①层循环固定x
      • 第②层循环固定y(元素不能重复使用，则初始化y=x+1)
      • 第③层循环双指针确定[u,v]
    • 剪枝 + 去重：处理过程对遍历范围进行控制，避免数组越界
      • 剪枝：对外层循环进行控制（预校验x+y+u+v与target的关系，避免无效的内层循环处理）
        • 固定元素，基于当前遍历元素连续取剩余的数构成的组合curSum>target则break跳出外层循环，后面的组合构成的和会越来越大
        • 固定元素，从数组末尾取剩余的数构成的组合curSum<target，则跳过当前组合continue，但是继续往前遍历那么固定的元素基于此构成的组合就会逐渐变大接近target，因此还是需要继续遍历的
      • 去重：避免连续重复的元素选择

常见题型

🟢242-有效的字母异位词

题目内容

给定两个字符串 s 和 t ，编写一个函数来判断 t 是否是 s 的 字母异位词

示例 1:

输入: s = "anagram", t = "nagaram"
输出: true

示例 2:

输入: s = "rat", t = "car"
输出: false

2.题解思路

• 思路分析：字母异位词（即使用A字符串中的字符可以构成字符串B）
  • 【1】计数法：A、B两个字符串的字符统计完全匹配
  • 【2】排序法：A、B两个字符串排序后可以得到完全一致的字符串序列
  • 【3】比较移除法：固定遍历字符串A，如果A中的字符在B中存在则移除B中指定的字符，当A遍历完成时B如果满足字母异位词的条件的话则此时B应该为空

👻方法1：计数法

• 思路分析：分别统计两个字符串中每个字符出现次数，然后一一比较判断每个字符出现的次数是否一致

/**
 * 有效的字母异位词（242）
 */
public class Solution1 {

    // 【1】计数法
    public boolean isAnagram(String s, String t) {
        // 如果两个字符串长度不一致则必然非字母异位词
        if(s.length() != t.length()){
            return false;
        }
        // 分别获取两个字符串的统计集合
        Map<Character,Integer> smap = getCharacterNum(s);
        Map<Character,Integer> tmap = getCharacterNum(t);
        // 遍历集合判断字符和出现次数是否完全匹配
        Iterator iterator = smap.entrySet().iterator();
        while (iterator.hasNext()){
            Map.Entry<Character,Integer> entry = (Map.Entry<Character,Integer>)iterator.next();
            if(tmap.get(entry.getKey())!=entry.getValue()){
                return false;
            }
        }
        // 校验通过
        return true;
    }

    // 定义方法统计两个字符串中每个字符出现的次数
    public Map<Character,Integer> getCharacterNum(String str){
        Map<Character,Integer> map = new HashMap<>();
        for(char ch : str.toCharArray()){
            map.put(ch,map.getOrDefault(ch,0)+1);
        }
        return map;
    }
}

• 复杂度分析

  • 时间复杂度：O（N）需分别遍历两个字符串，然后统计字符出现次数

  • 空间复杂度：O（x）需分别统计两个字符串中字符的出现次数，需借助辅助集合存储

另一种计数的思路

• （1）定义一个数组int[]存放a-z中所有字符的出现次数
• （2）遍历字符串s统计次数（累加）
• （3）遍历字符串t使用字符（递减）：表示当前已有的字符集中取出字符，如果取的过程中发现待使用的次数为0则说明不一致

/**
 * 有效的字母异位词（242）
 */
public class Solution12 {

    // 【1】计数法（定义字符序列的出现次数集合：使用数组实现）
    public boolean isAnagram(String s, String t) {
        // 如果两个字符串长度不一致则必然非字母异位词
        if (s.length() != t.length()) {
            return false;
        }

        // 1.定义数组存放`a`-`z`字符序列的出现次数
        int[] letterNum = new int[26];
        // 2.遍历字符串s统计字符出现次数
        for (int i = 0; i < s.length(); i++) {
            char cur = s.charAt(i); // 此时cur为字符形式，需转化为数组下标存储：'a'对应 0 需进行转化则需减去'a'
            letterNum[cur - 'a']++; // 累加统计
        }
        // 3.遍历字符串t，从目前现有的字符集合中取出元素，如果集合中没有足够的次数，说明不匹配
        for (int i = 0; i < t.length(); i++) {
            char cur = t.charAt(i);
            if (letterNum[cur - 'a'] <= 0) {
                return false; // 次数不足说明不匹配
            } else {
                letterNum[cur - 'a']--; // 表示使用该字符一次
            }
        }

        // 校验通过
        return true;
    }

}

👻方法2：排序法

• 思路分析：两个字符串如果互为字母异位词，则其排序后的字符串序列是一致的

/**
 * 有效的字母异位词（242）
 */
public class Solution2 {
    // 【2】排序法
    public boolean isAnagram(String s, String t) {
        // 如果两个字符串长度不一致则必然非字母异位词
        if(s.length() != t.length()){
            return false;
        }
        // 分别对两个字符串序列进行排序，判断排序后的字符串序列是否完全一致
        char[] sArr = s.toCharArray();
        Arrays.sort(sArr);
        char[] tArr = t.toCharArray();
        Arrays.sort(tArr);
        // 校验
        return String.valueOf(sArr).equals(String.valueOf(tArr));
        // return Arrays.equals(sArr, tArr);
    }
}

• 复杂度分析

  • 时间复杂度：O（N logN）需分别遍历两个字符串（O（n）），且排序（O（n log n））也需额外的消耗

  • 空间复杂度：O（N）需借助辅助的字符数组存储和处理排序结果（排序辅助（O（n log n）））

👻方法3：比较移除法

• 思路分析：固定遍历某个字符串（A），然后判断当前指向的A的字符在B中是否存在，如果存在则移除该字符。当A中所有字符序列已经遍历完成，此时B如果满足与A互为字母异位词则B的长度需为0

/**
 * 有效的字母异位词（242）
 */
public class Solution3 {
    // 【3】比较移除法
    public boolean isAnagram(String s, String t) {
        // 如果两个字符串长度不一致则必然非字母异位词
        if (s.length() != t.length()) {
            return false;
        }
        /**
         * 遍历s字符串，判断s中的字符是否在t中存在，如果存在则移除t中的该字符，不存在说明不符合字母异位词条件
         * - 此处可以在循环中判断，遇到不匹配直接返回false
         * - 也可以直接调用替换方法，最后遍历完成校验t的长度是否为0即可
         */
        for (char cur : s.toCharArray()) {
            t = t.replaceFirst(cur + "", ""); // 替换第1个匹配cur字符的元素为空，表示移除
        }

        // 当s遍历完成，如果s与t互为字母异位词，则t应该为空
        return t.length() == 0;
    }
}

• 复杂度分析

  • 时间复杂度：O（n）遍历字符串消耗，调用替换函数消耗

  • 空间复杂度：O（1）无需占用额外的辅助集合，只涉及替换函数相关消耗

🟢349-两个数组的交集

题目内容

给定两个数组 nums1 和 nums2 ，返回 它们的 交集 。输出结果中的每个元素一定是 唯一 的。我们可以 不考虑输出结果的顺序 。

示例 1：

输入：nums1 = [1,2,2,1], nums2 = [2,2]
输出：[2]

示例 2：

输入：nums1 = [4,9,5], nums2 = [9,4,9,8,4]
输出：[9,4]
解释：[4,9] 也是可通过的

2.题解思路

👻方法1：哈希表（两个集合）

• 思路分析：先对两个数组进行去重（去重并加入到哈希表中），随后选定一个set进行遍历，判断元素是否在另一个集合中也存在，存在则说明是公共元素需加入结果集

/**
 * 两个数组的交集（349）
 */
class Solution2 {
    // 哈希表
    public int[] intersection(int[] nums1, int[] nums2) {
        // 如果nums1、nums2其中一个为空则公共集合为空
        if (nums1 == null || nums2 == null) {
            return null;
        }

        // 将nums1放入哈希表中
        Set<Integer> set1 = new HashSet<>();
        for (int num : nums1) {
            set1.add(num);
        }

        // 遍历nums2集合，如果元素存在于set中则为公共元素
        Set<Integer> set2 = new HashSet<>(); // 对nums2去重
        for (int num : nums2) {
            set2.add(num);
        }

        // 封装公共集合
        Set<Integer> commonSet = new HashSet<>();
        for (int num : set2) {
            if (set1.contains(num)) {
                commonSet.add(num);
            }
        }

        // 封装最终的结果集
        int[] res = new int[commonSet.size()];
        int cur = 0;// 定义结果集指针
        for (int num : commonSet) {
            res[cur++] = num;
        }

        // 返回结果
        return res; // 注意数组长度问题处理
        
        // resSet.stream().mapToInt(x -> x).toArray(); 借助封装函数将结果集Set转为数组
    }
}

• 复杂度分析

  • 时间复杂度：O(m+n)，其中 m 和 n 分别是两个数组的长度。使用两个集合分别存储两个数组中的元素需要 O(m+n) 的时间，遍历较小的集合并判断元素是否在另一个集合中需要 O(min(m,n)) 的时间

• 空间复杂度：O(m+n)，其中 m 和 n 分别是两个数组的长度。空间复杂度主要取决于两个集合

🟢202-快乐数

题目内容

编写一个算法来判断一个数 n 是不是快乐数。

「快乐数」 定义为：

• 对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和
• 然后重复这个过程直到这个数变为 1，也可能是 无限循环 但始终变不到 1
• 如果这个过程 结果为 1，那么这个数就是快乐数

如果 n 是 快乐数 就返回 true ；不是，则返回 false

示例 1：

输入：n = 19
输出：true
解释：
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1

示例 2：

输入：n = 2
输出：false

2.题解思路

👻方法1：哈希表

• 思路分析：相当于不断去计算将某个正整数各个数位的平方和getN，如果这个数不为1则一直持续计算（当出现循环数：即getN已经出现过在集合中时则跳出循环）
  • 分析不断计算数位平方和的跳出条件：
    • 当计算得到一个快乐数：即getN==1时不需要继续计算下去
    • 当计算得到一个循环数：即getN在之前的计算中已经出现过，如果再次出现则会导致循环问题出现，因此这个n不可能是快乐数（基于此联想到引用哈希表来快速判断元素是否已经出现过）
  • 易错点：注意拆分方法实现，确保逻辑清晰，避免概念混淆。例如此处涉及到计算数位平方和可以单独抽离出一个方法实现（表示获取下一个要计算的数）

/**
 * 202 快乐数
 */
public class Solution1 {

    public boolean isHappy(int n) {
        // 定义集合存放数字（判断calN是否已经出现过集合中且非1）
        Set<Integer> set = new HashSet<>();
        int getN = calN(n);
        set.add(getN);

        while (getN != 1) {
            getN = calN(getN);
            // 判断是否出现在集合中
            if (set.contains(getN)) {
                return false; // 出现循环
            } else {
                set.add(getN);
            }
        }

        // 跳出循环说明最终为1
        return true;
    }

    public int calN(int n) {
        // 计算 n (每个位数的平方之和)
        int calN = 0;
        while (n != 0) {
            // 获取个位上的数字，拿到平方和
            calN += (n % 10) * (n % 10);
            n = n / 10; // 数位分离继续计算下一个位置
        }
        // 返回计算结果
        return calN;
    }

}

• 复杂度分析

  • 时间复杂度：O(243⋅3+logn+loglogn+logloglogn)... = O(logn)
    • 查找给定数字的下一个值的成本为 O(logn)，因为处理数字中的每位数字，而数字中的位数由 logn 给定。要计算出总的时间复杂度，需要仔细考虑循环中有多少个数字，它们有多大
    • 可以通过穷举法确认，一旦一个数字低于 243，它就不可能回到 243 以上。因此，就可以用 243 以下最长循环的长度来代替 243，不过，因为常数无论如何都无关紧要，所以不会担心它。
    • 对于高于 243 的 n，需要考虑循环中每个数高于 243 的成本。通过数学运算，可以证明在最坏的情况下，这些成本将是 O(logn)+O(loglogn)+O(logloglogn)...。O(logn) 是占主导地位的部分，而其他部分相比之下都很小（总的来说，它们的总和小于logn），所以可以忽略它们
  • 空间复杂度：O(logn) 需借助哈希集合存储计算过的元素

leetCode 官解版本

class Solution {
    private int getNext(int n) {
        int totalSum = 0;
        while (n > 0) {
            int d = n % 10;
            n = n / 10;
            totalSum += d * d;
        }
        return totalSum;
    }

    public boolean isHappy(int n) {
        Set<Integer> seen = new HashSet<>();
        while (n != 1 && !seen.contains(n)) {
            seen.add(n);
            n = getNext(n);
        }
        return n == 1;
    }
}

👻方法2：穷举法（数学规律法）

• 思路分析：通过穷举寻找数学规律，把所有的"循环数"敲定下来，如果通过计算得到的结果是在循环数中则非快乐数，否则一直计算下去直到确认是否可以得到1
  • 4→16→37→58→89→145→42→20→4

class Solution {

    private static Set<Integer> cycleMembers =
        new HashSet<>(Arrays.asList(4, 16, 37, 58, 89, 145, 42, 20));

    public int getNext(int n) {
        int totalSum = 0;
        while (n > 0) {
            int d = n % 10;
            n = n / 10;
            totalSum += d * d;
        }
        return totalSum;
    }


    public boolean isHappy(int n) {
        while (n != 1 && !cycleMembers.contains(n)) {
            n = getNext(n);
        }
        return n == 1;
    }
}

• 复杂度分析

  • 时间复杂度：O(logN)
  • 空间复杂度：O(1) 硬编码哈希集是一开始就固定下来的，在计算过程中只用到常数级别的空间占用

👻方法3：快慢指针

• 思路分析：将问题转化为链表（判断链表中是否存在环），因此可以采用快慢指针"龟兔赛跑"的思路去检测
  • 此处当前数为n，而下一个数getNext可以理解为next指针指向，基于此将思路转化为链表实现

class Solution {

     public int getNext(int n) {
        int totalSum = 0;
        while (n > 0) {
            int d = n % 10;
            n = n / 10;
            totalSum += d * d;
        }
        return totalSum;
    }

    public boolean isHappy(int n) {
        int slowRunner = n;
        int fastRunner = getNext(n);
        while (fastRunner != 1 && slowRunner != fastRunner) {
            slowRunner = getNext(slowRunner);
            fastRunner = getNext(getNext(fastRunner));
        }
        return fastRunner == 1;
    }
}

• 复杂度分析

  • 时间复杂度：O(logn)。该分析建立在对前一种方法的分析的基础上，但是这次需要跟踪两个指针而不是一个指针来分析，以及在它们相遇前需要绕着这个循环走多少次
    • 如果没有循环，那么快跑者将先到达 1，慢跑者将到达链表中的一半。最坏的情况下，成本是 O(2⋅logn)=O(logn)
    • 一旦两个指针都在循环中，在每个循环中，快跑者将离慢跑者更近一步。一旦快跑者落后慢跑者一步，他们就会在下一步相遇。假设循环中有 k 个数字。如果他们的起点是相隔 k−1 的位置（这是他们可以开始的最远的距离），那么快跑者需要 k−1 步才能到达慢跑者，这对于我们的目的来说也是不变的。因此，主操作仍然在计算起始 n 的下一个值，即 O(logn)
  • 空间复杂度：O(1)，对于这种方法，我们不需要哈希集来检测循环。指针需要常数的额外空间

基于"龟兔赛跑"的快慢指针

/**
 * 202 快乐数
 */
public class Solution2 {

    public boolean isHappy(int n) {
        // 转化为链表是否存在环的思路（龟兔赛跑）
        int slow = n;
        int fast = n; // int fast = calN(n); 以覆盖所有用例
        while (fast != 1) {
            slow = calN(slow);
            fast = calN(calN(fast));
            if (slow == fast) {
                return false; // 指针相遇说明存在环，即非快乐数返回false
            }
        }
        // 跳出循环说明fast先走到终点1
        return true;
    }

    public int calN(int n) {
        // 计算 n (每个位数的平方之和)
        int calN = 0;
        while (n != 0) {
            // 获取个位上的数字，拿到平方和
            calN += (n % 10) * (n % 10);
            n = n / 10; // 数位分离继续计算下一个位置
        }
        // 返回计算结果
        return calN;
    }
}

🟢001-两数之和

题目内容

给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出 和为目标值 target 的那 两个 整数，并返回它们的数组下标。

你可以假设每种输入只会对应一个答案，并且你不能使用两次相同的元素。

你可以按任意顺序返回答案。

示例 1：

输入：nums = [2,7,11,15], target = 9
输出：[0,1]
解释：因为 nums[0] + nums[1] == 9 ，返回 [0, 1] 。

示例 2：

输入：nums = [3,2,4], target = 6
输出：[1,2]

示例 3：

输入：nums = [3,3], target = 6
输出：[0,1]

2.题解思路

👻方法1：哈希表

• 思路分析：借助哈希表存储已遍历元素，在遍历数组的同时从已遍历元素集合中检索是否存在两数之和为target的元素，此处用HashMap存储数据（key 数组元素，value 元素对应下标）

// 哈希表
public int[] twoSum(int[] nums, int target) {
    // 定义哈希表存储元素：key(nums[i]) value(i 对应数组下标)
    Map<Integer, Integer> map = new HashMap<>();

    for (int i = 0; i < nums.length; i++) {
        if (map.containsKey(target - nums[i])) {
            return new int[]{map.get(target - nums[i]), i}; // 遍历过程中校验是否现存满足两数之和为target的内容
        } else {
            map.put(nums[i], i); // 加入哈希集合
        }
    }
    // 没有满足两数之和为target的场景
    return new int[]{0, 0};
}

• 复杂度分析

  • 时间复杂度：O（n）n 为数组长度，仅需单次遍历即可

  • 空间复杂度：O（n）

👻方法2：暴力法❌

• 思路分析：双层暴力循环遍历数组，寻找满足两数之和为target且不重复使用的元素

// 暴力法
public int[] twoSum(int[] nums, int target) {
    for (int i = 0; i < nums.length - 1; i++) {
        for (int j = i + 1; j < nums.length; j++) {
            if (nums[i] + nums[j] == target) {
                return new int[]{i, j};
            }
        }
    }
    // 没有满足两数之和为target的场景
    return new int[]{0, 0};
}

• 复杂度分析

  • 时间复杂度：O（n²）n 为数组长度，需双重遍历依次比较数组中的两个数

  • 空间复杂度：O（1）遍历过程中没有涉及辅助集合的使用，仅用到常数级别的占用

🟡454-四数相加II

题目内容

给你四个整数数组 nums1、nums2、nums3 和 nums4 ，数组长度都是 n ，请你计算有多少个元组 (i, j, k, l) 能满足：

• 0 <= i, j, k, l < n
• nums1[i] + nums2[j] + nums3[k] + nums4[l] == 0

示例 1：

输入：nums1 = [1,2], nums2 = [-2,-1], nums3 = [-1,2], nums4 = [0,2]
输出：2
解释：
两个元组如下：
1. (0, 0, 0, 1) -> nums1[0] + nums2[0] + nums3[0] + nums4[1] = 1 + (-2) + (-1) + 2 = 0
2. (1, 1, 0, 0) -> nums1[1] + nums2[1] + nums3[0] + nums4[0] = 2 + (-1) + (-1) + 0 = 0

示例 2：

输入：nums1 = [0], nums2 = [0], nums3 = [0], nums4 = [0]
输出：1

2.题解思路

👻方法1：分组+哈希表

• 思路分析：两两分组进行和统计，然后参考两数之和的思路
  • （1）AB数组为一组进行双层循环统计每个和出现的次数Map<两数之和,该和出现次数>
  • （2）CD数组为一组进行双层循环计算和，并按照两数之和的思路判断0-curSum(即相反数)是否存在于步骤1构建的哈希集合中，如果存在则进行计数统计（看当前遍历的curSum和步骤1中出现了多少次相反数进行累加）
• 易错点：此处思路很容易顺拐去优先分组统计AB、CD各自的和出现的次数，然后再遍历一遍去匹配x+y=0的情况，但这样的话就涉及到额外的遍历成本和重复情况的处理，因此还是基于分组+两数之和的思路去做更为合适

// 暴力法：分组 + 哈希表
public int fourSumCount(int[] nums1, int[] nums2, int[] nums3, int[] nums4) {
    /**
         * 根据数组进行两两分组：
         * 1.对每组数组进行`u+v`结果计算（双层循环）：统计每个和出现的次数，加入哈希表中存储Map<两数之和,该和出现次数>
         * 2.对步骤1中得到的两个哈希集合进行遍历，看是否存在x+y=0的情况，存在则进行统计
         */
    // nums1、nums2一组
    HashMap<Integer, Integer> map1 = new HashMap<>();
    for (int i = 0; i < nums1.length; i++) {
        for (int j = 0; j < nums2.length; j++) {
            int curSum = nums1[i] + nums2[j];
            map1.put(curSum, map1.getOrDefault(curSum, 0) + 1);
        }
    }

    // nums3、nums4一组(遍历的时候进行判断)
    int res = 0;
    for (int k = 0; k < nums3.length; k++) {
        for (int l = 0; l < nums4.length; l++) {
            int curSum = nums3[k] + nums4[l];
            if (map1.containsKey(-1 * curSum)) { // 如果集合中存在匹配x+y=0的值则计数
                res += map1.get(-1 * curSum);
            }
        }
    }

    // 返回统计结果
    return res;
}

• 复杂度分析

  • 时间复杂度：O（n²）需对数组进行分组求两个数组元素之和出现的次数，然后进行判断

  • 空间复杂度：O（n²）需借助哈希表存储两个数组元素之和出现的次数，最坏的情况就是n × n

另一种写法：中规中矩求解

/**
 * 🟡 454 四数相加II - https://leetcode.cn/problems/4sum-ii/description/
 */
public class Solution454_01 {

    /**
     * 思路分析：计算有多少个元组满足a+b+c+d=0
     * 两两处理：nums1+nums2得到map1(和及其构成元组数)、nums1+nums2得到map2(和及其构成元组数)
     * 然后基于哈希表的思路校验map1+map2=0
     */
    public int fourSumCount(int[] nums1, int[] nums2, int[] nums3, int[] nums4) {
        // 两两处理，获取数组和映射
        Map<Integer, Integer> map1 = getSumMap(nums1, nums2);
        Map<Integer, Integer> map2 = getSumMap(nums3, nums4);
        // 基于哈希思路校验map1[i]+map2[j]=0的情况并统计元组个数
        int res = 0;
        Set<Integer> keySet = map2.keySet();
        for (int key : keySet) {
            if (map1.containsKey(0 - key)) {
                res += map1.get(0 - key) * map2.get(key);
            }
        }
        // 返回结果
        return res;
    }

    // 计算两个数组元素和的出现次数
    private Map<Integer, Integer> getSumMap(int[] nums1, int[] nums2) {
        // 计算nums1与nums2可构成的和元组情况
        Map<Integer, Integer> map = new HashMap<>();
        for (int i = 0; i < nums1.length; i++) {
            for (int j = 0; j < nums2.length; j++) {
                int sum = nums1[i] + nums2[j];
                map.put(sum, map.getOrDefault(sum, 0) + 1);
            }
        }
        return map;
    }
}

👻方法2：暴力法❌（超时）

• 思路分析：双层暴力循环遍历数组，寻找满足两数之和为target且不重复使用的元素

// 暴力法：四层循环
public int fourSumCount(int[] nums1, int[] nums2, int[] nums3, int[] nums4) {
    int res = 0;
    for (int i = 0; i < nums1.length; i++) {
        for (int j = 0; j < nums2.length; j++) {
            for (int k = 0; k < nums3.length; k++) {
                for (int l = 0; l < nums4.length; l++) {
                    if (nums1[i] + nums2[j] + nums3[k] + nums4[l] == 0) {
                        res++;
                    }
                }
            }
        }
    }
    // 返回统计结果
    return res;
}

• 复杂度分析

  • 时间复杂度：O（n²）n 为数组长度，需双重遍历依次比较数组中的两个数

  • 空间复杂度：O（1）遍历过程中没有涉及辅助集合的使用，仅用到常数级别的占用

🟢383-赎金信

题目内容

给你两个字符串：ransomNote 和 magazine ，判断 ransomNote 能不能由 magazine 里面的字符构成。

如果可以，返回 true ；否则返回 false 。

magazine 中的每个字符只能在 ransomNote 中使用一次。

2.题解思路

👻方法1：计数法

• 思路分析：统计magazine中每个字符的出现次数（Map<字符，出现次数>），然后循环遍历ransomNote中的字符，如果存在匹配则从map取出字符（-1），不匹配则说明不满足
  • ==补充：==类似地，这种字符统计也可以使用数组来实现（定义一个存储26个字符出现次数的数字，将a字符和数组下标相对应）。此处选用map存储则更加灵活

// 思路：计数法
public boolean canConstruct(String ransomNote, String magazine) {
    // 统计magazine中每个字符的出现次数
    Map<Character,Integer> map = new HashMap<>();
    for(char ch : magazine.toCharArray()){
        map.put(ch,map.getOrDefault(ch,0)+1);
    }

    // 遍历ransomNote字符，判断是否匹配
    for(char ch : ransomNote.toCharArray()){
        if(map.containsKey(ch) && map.get(ch) > 0){ // 存在匹配字符，且使用次数大于0
            // 取出字符进行使用
            map.put(ch,map.get(ch)-1);
        }else{
            // 不存在匹配字符 或者 字符被用完了
            return false;
        }
    }

    return true;
}

• 复杂度分析

  • 时间复杂度：O（m+n） 需遍历两个字符串内容

  • 空间复杂度：O（m）需借助辅助哈希表存储magazine中字符出现的次数（m为magazine字符串长度）

🟡015-三数之和

题目内容

给你一个整数数组 nums ，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ，同时还满足 nums[i] + nums[j] + nums[k] == 0 。请你返回所有和为 0 且不重复的三元组。

**注意：**答案中不可以包含重复的三元组

示例 1：

输入：nums = [-1,0,1,2,-1,-4]
输出：[[-1,-1,2],[-1,0,1]]
解释：
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意，输出的顺序和三元组的顺序并不重要。

示例 2：

输入：nums = [0,1,1]
输出：[]
解释：唯一可能的三元组和不为 0 。

示例 3：

输入：nums = [0,0,0]
输出：[[0,0,0]]
解释：唯一可能的三元组和为 0 。

2.题解思路

👻方法1：排序+双指针遍历法（❌ 超时）

• 思路分析：对数组元素进行排序，随后循环遍历数组元素，固定一位并通过双指针方式查找另外两位可以与之构成三元组的元素
  • 易错点：去重处理、指针移动，一些遍历过程中的细节要注意
  • 超时限制：在遍历的过程中注意对一些情况做校验排除，从而降低时间复杂度
    • 例如 如果 num[i] > 0 则其后面根本不可能构成 target 为0的三元组，直接排除（因为数组已递增排序）
    • 在遍历的过程中需要对数组元素进行去重处理
  • 如何剪枝：从[x,y,z] => x+y+z=0这一条件出发进行思考，充分利用数组有序性
    • 剪枝①x>0（控制外层循环（对x的遍历优化））：直接剪（因为数组有序，则x<=y<=z始终满足，如果x>0成立则根本无法选出满足条件的三元组（因为此时y、z金额肯定为大于0的））
    • 剪枝②[x,y,z]：数组本身有序，如果x确定，则[y,z]也必然限定，如果再次出现连续重复的x则其可构成的三元组已经被前面的情况覆盖了，无需重复处理。因此对于连续出现的x需跳过（只保留第一个x的处理结果即可）
    • 剪枝③[y,z]：同理，当x确定后，[y,z]的确定也是类似，y确定了则z必然确定，z确定了则y必然确定，基于双向指针的考虑，在处理完一组三元组后，如果发现出现重复的y或者z直接跳过，继续下一个非重复的校验位置即可（对于y、z的处理需注意数组下标越界问题，对有效的索引取值范围进行校验）

/**
 * 015 三数之和
 */
public class Solution1 {

    // 思路分析：对数组元素进行排序，固定 i ，然后分别从i+1\len-1位置向中间靠拢寻找三元组
    public List<List<Integer>> threeSum(int[] nums) {
        // 定义结果集
        List<List<Integer>> res = new ArrayList<>();

        // 1.对数组进行排序
        Arrays.sort(nums);

        // 2.固定i，然后分别从i+1\len-1位置向中间靠拢寻找三元组
        for (int i = 0; i < nums.length - 2; i++) { // 三元组边界，i只需要遍历到倒数第3个位置
            int left = i + 1, right = nums.length - 1; // 定义左右指针，辅助寻找三元组
            while (left < right) { // 元素不能重复
                List<Integer> temp = new ArrayList<>();
                int curSum = nums[i] + nums[left] + nums[right];
                if (curSum == 0) {
                    // 构成三元组，记录集合(此处记录的是元素，而非下标)
                    temp.add(nums[i]);
                    temp.add(nums[left]);
                    temp.add(nums[right]);
                    // 将其加入结果集合(需进行去重处理)
                    if(!res.contains(temp)){
                        res.add(new ArrayList<>(temp));
                    }
                    // 当前三元组判断完成，继续下一个判断，两个指针都向中间靠拢
                    left++;
                    right--;
                } else {
                    // 指针继续移动（判断左右指针移动方向，将curSum与0做对比）
                    if (curSum < 0) {
                        // 和小于0，则要让curSum变大
                        left++;
                    } else if (curSum > 0) {
                        // 和大于0，则要让curSum变小
                        right--;
                    }
                }
            }
        }
        // 返回结果集
        return res;
    }

}

• 复杂度分析

  • 时间复杂度：O（n²）n 为nums数组长度

  • 空间复杂度：O（logN）忽略结果集的存储占用空间的话，此处空间占用只涉及到一个数组元素排序

剪枝分析

​ 基于nums[]的有序性，选择性进行剪枝操作，进而优化算法效率。可以从两个主要方面切入：

① target为 0：既然限定了三元组之和为0，那么考虑到数组的有序性，如果第一个选出的元素就已经大于0则没有必要校验其可能的三元组

• 因为对于[x,y,z]三元组而言，如果基于排序+双指针的做法，则选出的三元组必然满足x<=y<=z，因此如果选出的第1个元素如果满足x>0，则其后的元素肯定是大于0的，则组合选择更加不可能构成target=0的三元组，因此可以直接跳过这个元素

  for (int i = 0; i < nums.length - 2; i++) { // 三元组，所以i取值范围为[0,n-2）
      // 剪枝①：nums在前面进行了排序，如果固定的nums[i]>0,则后面的数只会更大不可能构成三元组和为0，直接跳过
      if (nums[i] > 0) {
          continue;
      }
      ...... [y,z] 的确定过程（双指针遍历）......
  }
  

② 限定三元组不可出现重复的集合

• 原限定根据res.contains(temp)这一条件校验三元组是否重复，之所以可以通过这一条件限定，是因为数组元素有序，所以构成的三元组是按照元素大小排序的，那么这种情况下不会通过这种方式是可以对三元组进行去重的（如果无序的话则失效，因为list(-1,0,1)和list(0,-1,1)是两个完全不同的集合）。但是通过这种去重的校验方式会出现一个问题，就是当数组较大的时候，会出现超时限制，因此要想办法优化这块的内容

• 由于数组有序，因此相同元素会连续出现，那么就要思考如何有效跳过这些可能导致重复的情况而不用contains硬核判断

  • 以[-1,-1,0,1]为例，可以看到满足条件的三元组[x,y,z]应该为[-1,0,1]，但是实际在遍历的过程中，它会按照顺序定位i，也就是说它会处理两次x=-1的情况，但实际上此处很明显就是出现重复了。因为数组元素本身有序，那么当确定了x，则无非就是确定后面的[y,z]，后面出现了同样x其可构成的满足条件的三元组本身就会被前面出现的情况覆盖了，所以对于此处连续重复出现的x只需要校验第一个出现的x即可。因此此处可以限定一个剪枝条件：

    for (int i = 0; i < nums.length - 2; i++) { // 三元组，所以i取值范围为[0,n-2）
        // 剪枝①：nums在前面进行了排序，如果固定的nums[i]>0,则后面的数只会更大不可能构成三元组和为0，直接跳过
        if (nums[i] > 0) {
            continue;
        }
    
        // 剪枝②：如果出现重复三元组则跳过（nums已经确定了有序，因此此处如果校验三元组的第一个元素相同的话，已经先出现的元素情况覆盖了，不需要重复处理）
        if (i > 0 && nums[i] == nums[i - 1]) {
            continue; // 例如[-1,-1,0,0]: 第一个元素为-1的满足三元组的情况已经在前面就确定了，如果发现相邻相同的话则跳过
        }
        
        ...... [y,z] 的确定过程（双指针遍历）......
    }
    

  • 同理，在确定[y,z]的时候，既然y确定了，那么当连续出现同样的y的话就会导致重复，直接跳过连续的y即可。且此处是双向指针的限定，也就是说实际上当确定了y则其z随之确定，当确定了z则其y也随之确定，因此对于双向指针来说，都需要在限定条件下去跳过这些导致重复的元素，因此第③个剪枝体现在[y,z]的选择上

    • 可以结合案例理解分析[-2,0,0,0,2,2,2]
      • 当x=-2确定，此时从剩余的序列[0,0,0,2,2,2]选出[y,z]，指针从头尾各自出发选出了[0,2]恰好满足三元组。如果继续遍历会发现，当出现了连续重复的y或者z则构成的三元组必然是被前面情况覆盖了的，因此此处需要跳过这些连续重复的元素，以做到集合去重的平替

    // 针对选择[y,z]的处理过程
    while (left < right) {
        // 定义临时三元组集合
        List<Integer> temp = new ArrayList<>();
        int curSum = nums[i] + nums[left] + nums[right];
        // 校验是否满足三元组条件
        if (curSum == 0) {
            temp.add(nums[i]);
            temp.add(nums[left]);
            temp.add(nums[right]);
    
            res.add(temp); // 直接加入（此处的contains校验已经通过剪枝处理了）
    
            // 本次处理完成，指针移动，继续下一个三元组遍历
            left++;
            right--;
    
            // 剪枝③：[y,z]的选择，如果y、z出现连续重复则跳过（因为在前面的处理中已唯一确定）
            while (left < right && nums[left - 1] == nums[left]) { // 左指针控制：y重复则跳过
                left++;
            }
            while (left < right && nums[right] == nums[right + 1]) { // 右指针控制：z重复则跳过
                right--;
            }
    
        } else if (curSum < 0) {
            // curSum<0，要让其变大才可能接近target
            left++;
        } else if (curSum > 0) {
            // curSum>0，要让其变小才可能接近target
            right--;
        }
    }
    

剪枝优化版本代码参考

/**
 * 🟡015 三数之和 （剪枝优化）
 */
public class Solution015_02 {

    /**
     * 【排序+双指针】：从一个整数数组`nums`中获取到满足`x+y+z=0`且不重复的三元组
     * - ① 对`nums`进行排序（为了便于通过指针定位三元组）
     * - ② 外层固定`i`，内层通过双指针分别从剩余的序列的头尾向中间靠拢寻找三元组(根据当前组合和决定指针更新方向)
     */
    public List<List<Integer>> threeSum(int[] nums) {
        // 定义结果集
        List<List<Integer>> res = new ArrayList<>();
        // ① 对nums排序
        Arrays.sort(nums);
        // ② 遍历检索三元组（外层固定i，内层从剩余序列的头尾出发，定位三元组）
        for (int i = 0; i < nums.length - 2; i++) { // 三元组，所以i取值范围为[0,n-2）
            // 剪枝①：nums在前面进行了排序，如果固定的nums[i]>0,则后面的数只会更大不可能构成三元组和为0，直接跳过
            if (nums[i] > 0) {
                continue;
            }

            // 剪枝②：如果出现重复三元组则跳过（nums已经确定了有序，因此此处如果校验三元组的第一个元素相同的话，已经先出现的元素情况覆盖了，不需要重复处理）
            if (i > 0 && nums[i] == nums[i - 1]) {
                continue; // 例如[-1,-1,0,0]: 第一个元素为-1的满足三元组的情况已经在前面就确定了，如果发现相邻相同的话则跳过
            }

            // 构建双指针，检索满足条件的三元组
            int left = i + 1, right = nums.length - 1;
            while (left < right) {
                // 定义临时三元组集合
                int curSum = nums[i] + nums[left] + nums[right];
                // 校验是否满足三元组条件
                if (curSum == 0) {
                    // res 的去重校验（contains）通过剪枝来处理，此处可以直接加入
                    res.add(Arrays.asList(nums[i], nums[left], nums[right]));

                    // 本次处理完成，指针移动，继续下一个三元组遍历
                    left++;
                    right--;

                    // 剪枝③：[y,z]的选择，如果y、z出现连续重复则跳过（因为在前面的处理中已唯一确定）
                    while (left < right && nums[left - 1] == nums[left]) { // 左指针控制：y重复则跳过
                        left++;
                    }
                    while (left < right && nums[right] == nums[right + 1]) { // 右指针控制：z重复则跳过
                        right--;
                    }
                } else if (curSum < 0) {
                    left++; // curSum<0，要让其变大才可能接近target
                } else if (curSum > 0) {
                    right--;  // curSum>0，要让其变小才可能接近target
                }
            }
        }

        // 返回最终结果
        return res;
    }
}

​ 可以看到从【超时限制】优化后性能大大提升

🟡018-四数之和

题目内容

​ 给你一个由 n 个整数组成的数组 nums ，和一个目标值 target 。请你找出并返回满足下述全部条件且不重复的四元组 [nums[a], nums[b], nums[c], nums[d]] （若两个四元组元素一一对应，则认为两个四元组重复）：

• 0 <= a, b, c, d < n
• a、b、c 和 d 互不相同
• nums[a] + nums[b] + nums[c] + nums[d] == target

你可以按 任意顺序 返回答案 。

示例 1：

输入：nums = [1,0,-1,0,-2,2], target = 0
输出：[[-2,-1,1,2],[-2,0,0,2],[-1,0,0,1]]

示例 2：

输入：nums = [2,2,2,2,2], target = 8
输出：[[2,2,2,2]]

2.题解思路

👻方法1：排序+双指针

• 思路：和三元组的求解思路类似，此处固定两个位置，然后双指针从剩余元素的头尾向中间靠拢

// 排序 + 双指针 （仿三元组的思路，此处固定两个位置，然后双指针从剩余元素的头尾向中间靠拢）
public List<List<Integer>> fourSum(int[] nums, int target) {
    // 定义结果集
    List<List<Integer>> res = new ArrayList<>();
    // 1.排序：对数组进行排序
    Arrays.sort(nums);

    // 2.双指针：双指针验证四元组
    for (int i = 0; i < nums.length - 3; i++) {
        for (int j = i + 1; j < nums.length - 2; j++) {
            int left = j + 1, right = nums.length - 1;
            while (left < right) {
                int curSum = nums[i] + nums[j] + nums[left] + nums[right];
                // 判断curSum与target的关系，以此确定指针移动方向
                if (curSum == target) {
                    List<Integer> temp = new ArrayList<>();
                    temp.add(nums[i]);
                    temp.add(nums[j]);
                    temp.add(nums[left]);
                    temp.add(nums[right]);
                    // 判断是否存在集合，不存在重复则补充
                    if (!res.contains(temp)) {
                        res.add(temp);
                    }
                    // 指针继续移动，判断下一个匹配的四元组
                    left++;
                    right--;
                } else if (curSum < target) {
                    // 需要让curSum变大
                    left++;
                } else if (curSum > target) {
                    // 需要让curSum变小
                    right--;
                }
            }
        }
    }
    // 返回结果集合
    return res;
}

• 复杂度分析

  • 时间复杂度：O（n³）n 为nums数组长度

  • 空间复杂度：O（logN）忽略结果集的存储占用空间的话，此处空间占用只涉及到一个数组元素排序

细节补充

• 数值溢出问题：累加和可能导致数值溢出，因此用long进行处理
• 特殊情况处理：对于一些特殊情况的判断（减枝处理），可以降低时间复杂度
  • 此处对比015-三数之和的思路，虽然核心思路大差不差，但是一些条件的限制却有所不同。需要注意此处校验的是一个target（不限定取值），而三数之和中校验的是0。因此以[x,y,u,v]为例，两种场景的处理不能一概而论：
    • ① 对于【三数之和】中的处理，基于数组有序（x<=y<=u<=v）如果x>0成立的话，那么后面的y、u、v必然也是大于0的数，因此x+y+u+v的组合不可能构成0
    • ② 而对于【四数之和】中的处理，基于数组有序（x<=y<=u<=v）如果x>target成立的话，并不能参照①的校验。因为对于如果x取负数的情况下，是可以通过累加来接近target，如果限定x>target为剪枝条件而跳过的话，举个最简单的例子，就会错过这一情况[-4,-3,-2,-1] target=-10，因此很明显，对于剪枝的处理是针对正负数的考虑，而不是针对target
  • 剪枝(对外层循环的控制) 和 去重(对结果集重复的处理) 方向：充分利用数组有序的特性
    • 剪枝：此处剪枝是直接预先校验curSum = x+y+u+v与target的关系（控制外层循环（对x、y的遍历优化）），避免下一层循环的无效遍历
      • 以nums[x]校验为例
        • ① 如果连续构成的四个数满足curSum(nums[x]+nums[x+1]+nums[x+2]+nums[x+3]) > target则中断（break）（后面构成的组合数只会越来越大，根本无法选出满足条件的组合，因此可以直接break外层循环）
        • ② 如果x加上数组末尾的3个数满足curSum(nums[x]+nums[n-3]+nums[n-2]+nums[n-3]) < target则跳过（continue），但是需注意虽然当下组合不满足可以跳过，但是后面的元素选择会越来越大，则会慢慢接近target，因此还是要继续遍历下去
      • 同理对于nums[y]的校验也是类似，只不过注意此处在第2层循环中固定了x、y，则还需另外取两个数进行校验
    • 去重：对于每个数，判断是否连续出现重复的数（出现连续重复则跳过，需注意数组越界问题）

/**
 * 🟡 018 四数之和（剪枝去重优化版本）
 */
public class Solution018_02 {

    /**
     * 降维+排序+双指针：求[x,y,u,v] => 求 基于 x 构成的 满足[y,u,v](y+u+v=target-x的三元组) 构成的四元组
     * 且x y u v 互不相同
     */
    public List<List<Integer>> fourSum(int[] nums, int target) {
        List<List<Integer>> res = new ArrayList<>();
        int n = nums.length;
        // ① 对数组进行排序
        Arrays.sort(nums);

        // ② 求[x,y,u,v] => 求 基于 x 构成的 满足[y,u,v](y+u+v=target-x的三元组) 构成的四元组
        for (int x = 0; x < n - 3; x++) { // 处理第1个数字
            // 剪枝①：控制外层循环（预比较当前组合值与target的关系）
            if (nums[x] + nums[x + 1] + nums[x + 2] + nums[x + 3] > target)
                break; // 【以x开始连续的4个数构成】后面的组合数更加不可能构成target
            if (nums[x] + nums[n - 3] + nums[n - 2] + nums[n - 1] < target)
                continue; // 【x 加上 数组末尾的3个数 构成】当前的组合数不能构成target，但还需继续遍历下去慢慢接近target

            // 去重①：x 去重（如果 x 出现连续重复则跳过）
            if (x > 0 && nums[x - 1] == nums[x]) continue;

            // 处理三元组
            for (int y = x + 1; y < n - 2; y++) { // 处理第2个数字
                // 剪枝②：控制外层循环（预比较当前组合值与target的关系）
                if (nums[x] + nums[y] + nums[y + 1] + nums[y + 2] > target)
                    break; // 【固定x、y，加上以y开始连续的2个数构成】后面的组合数更加不可能构成target
                if (nums[x] + nums[y] + nums[n - 2] + nums[n - 1] < target)
                    continue; // 【固定x、y 加上 数组末尾的2个数 构成】当前的组合数不能构成target，但还需继续遍历下去慢慢接近target

                // 去重②：y去重（如果 y 出现连续重复则跳过）
                if (y > x + 1 && nums[y - 1] == nums[y]) continue;

                // 定义双指针确定[u,v]
                int u = y + 1, v = n - 1;
                while (u < v) { // 双指针处理第3、4个数字
                    int curSum = nums[x] + nums[y] + nums[u] + nums[v];
                    if (curSum == target) {
                        res.add(new ArrayList<>(Arrays.asList(nums[x], nums[y], nums[u], nums[v]))); // 去重处理（Arrays.asList(nums[x], nums[y], nums[u], nums[v])）

                        // 当次处理完成，指针后移
                        u++;
                        v--;

                        while (u < v && nums[u - 1] == nums[u]) u++; // 去重③：u去重（如果 u 出现连续重复则跳过）
                        while (u < v && nums[v] == nums[v + 1]) v--; // 去重④：v去重（如果 v 出现连续重复则跳过）

                    } else if (curSum < target) u++;
                    else if (curSum > target) v--;
                }
            }
        }

        // 返回结果
        return res;
    }

    public static void main(String[] args) {
        int[] nums = new int[]{1, -2, -5, -4, -3, 3, 3, 5};
        Solution018_02 s = new Solution018_02();
        List<List<Integer>> ans = s.fourSum(nums, -11);
        System.out.println();
    }
}

👻方法2：降维（借助三数之和的思路）

• 思路：固定x，然后剩余y u v基于三数之和构建封装方法

/**
 * 🟡 018 四数之和（剪枝优化版本） todo 转化为三数之和
 */
public class Solution018_03 {

    /**
     * 降维+排序+双指针：求[x,y,u,v] => 求 基于 x 构成的 满足[y,u,v](y+u+v=target-x的三元组) 构成的四元组
     * 且x y u v 互不相同
     */
    public List<List<Integer>> fourSum(int[] nums, int target) {
        List<List<Integer>> res = new ArrayList<>();
        int len = nums.length;
        // ① 对数组进行排序
        Arrays.sort(nums);

        // ② 求[x,y,u,v] => 求 基于 x 构成的 满足[y,u,v](y+u+v=target-x的三元组) 构成的四元组

        // 固定 x
        for (int x = 0; x < len - 3; x++) {
            // 去重处理：如果出现连续重复的x则跳过
            if (x > 0 && nums[x - 1] == nums[x]) {
                continue;
            }

            // 求满足[y,u,v](y+u+v=target-x的三元组)
            int curTarget = target - nums[x];
            List<List<Integer>> threeSumList = threeSum(Arrays.copyOfRange(nums, x + 1, len), curTarget);
            for (int i = 0; i < threeSumList.size(); i++) {
                threeSumList.get(i).add(nums[x]);
                res.add(threeSumList.get(i));
            }
        }

        // 返回结果
        return res;
    }

    // 三元组求解
    public List<List<Integer>> threeSum(int[] nums, int target) {
        // 定义结果集
        List<List<Integer>> res = new ArrayList<>();
        // ① 对nums排序
        Arrays.sort(nums);
        // ② 遍历检索三元组（外层固定i，内层从剩余序列的头尾出发，定位三元组）
        for (int i = 0; i < nums.length - 2; i++) { // 三元组，所以i取值范围为[0,n-2）
            // 去重处理
            if (i > 0 && nums[i] == nums[i - 1]) {
                continue; // 例如[-1,-1,0,0]: 第一个元素为-1的满足三元组的情况已经在前面就确定了，如果发现相邻相同的话则跳过
            }

            // 构建双指针，检索满足条件的三元组
            int left = i + 1, right = nums.length - 1;
            while (left < right) {
                int curSum = nums[i] + nums[left] + nums[right];
                // 校验是否满足三元组条件
                if (curSum == target) {
                    // res 的去重校验（contains）通过剪枝来处理，此处可以直接加入
                    List<Integer> temp = new ArrayList<>();
                    temp.add(nums[i]);
                    temp.add(nums[left]);
                    temp.add(nums[right]);
                    res.add(temp); // Arrays.asList(nums[i], nums[left], nums[right])

                    // 本次处理完成，指针移动，继续下一个三元组遍历
                    left++;
                    right--;

                    while (left < right && nums[left - 1] == nums[left]) { // 左指针控制：y重复则跳过
                        left++;
                    }
                    while (left < right && nums[right] == nums[right + 1]) { // 右指针控制：z重复则跳过
                        right--;
                    }
                } else if (curSum < target) {
                    left++; // 要让其变大才可能接近target
                } else if (curSum > target) {
                    right--;  // 要让其变小才可能接近target
                }
            }
        }

        // 返回最终结果
        return res;
    }

    public static void main(String[] args) {
        int[] nums = new int[]{1, 0, -1, 0, -2, 2};
        Solution018_03 s = new Solution018_03();
        s.fourSum(nums, 0);
    }
}

🟢205-同构字符串

1.题目内容

给定两个字符串 s 和 t ，判断它们是否是同构的。

如果 s 中的字符可以按某种映射关系替换得到 t ，那么这两个字符串是同构的。

每个出现的字符都应当映射到另一个字符，同时不改变字符的顺序。不同字符不能映射到同一个字符上，相同字符只能映射到同一个字符上，字符可以映射到自己本身。

示例 1:

输入：s = "egg", t = "add"
输出：true

示例 2：

输入：s = "foo", t = "bar"
输出：false

示例 3：

输入：s = "paper", t = "title"
输出：true

2.题解思路

👻方法1：哈希表

• 思路分析：此处同构即映射概念，由于题目中并没有显式指定字符与字符的映射关系，可以理解为"先入为主"，优先匹配前面出现的字符对，如果发现map中不存在映射关系则新增，如果发现存在则基于现存的映射关系校验后出现的映射对是否匹配，如果不匹配则说明同一个字符映射到不同的字符上了，不满足题意

/**
 * 🟢 205 同构字符串
 */
public class Solution1 {

    // 哈希表
    public boolean isIsomorphic(String s, String t) {
        int sLen = s.length(), tLen = t.length();
        if (sLen != tLen) {
            // 长度不一致，无法匹配
            return false;
        }
        // 定义map存储现存的字符映射情况(Map<s,t>),以s为基础，t为对应的映射字符
        Map<Character, Character> map = new HashMap<>();
        for (int i = 0; i < sLen; i++) {
            char curS = s.charAt(i);
            char curT = t.charAt(i);
            if (map.containsKey(curS)) {
                // 字符映射关系已存在，校验是否一致(如果不一致则不满足同构条件) curS -> curT
                if (map.get(curS) != curT) {
                    return false;
                }
            } else if (map.containsValue(curT)) { // curT已有映射关系存在，且这个映射关系并不等于curS
                return false;
            } else {
                // 字符映射关系不存在，新增
                map.put(curS, curT);
            }
        }
        // 校验通过
        return true;
    }

    public static void main(String[] args) {
        // String s = "paper",t="title";
        String s = "badc", t = "baba";
        Solution1 solution1 = new Solution1();
        solution1.isIsomorphic(s, t);
    }
}

• 复杂度分析

  • 时间复杂度：O（n）同时遍历两个字符串

  • 空间复杂度：O（n）基于map构建映射关系

👻方法2：双Map处理（🔔）

• 思路分析：基于上述【方法1】的思路，此处为了避免处理混淆，选用两个map分别用于存储s->t、t->s的映射关系
  • 由于涉及到双向映射的问题，定义两个map分别构建映射关系，思路会更加清晰

/**
 * 🟢 205 同构字符串
 */
public class Solution2 {

    // 哈希表(双map处理)
    public boolean isIsomorphic(String s, String t) {
        int sLen = s.length(), tLen = t.length();
        if (sLen != tLen) {
            // 长度不一致，无法匹配
            return false;
        }
        // 定义map存储现存的字符映射情况(Map<s,t>),以s为基础，t为对应的映射字符
        Map<Character, Character> map1 = new HashMap<>(); // map1: s->t
        Map<Character, Character> map2 = new HashMap<>(); // map2: t->s
        for (int i = 0; i < sLen; i++) {
            char curS = s.charAt(i);
            char curT = t.charAt(i);
            if (!map1.containsKey(curS)) {
                map1.put(curS, curT); // 构建s->t的映射关系(先入为主，如果已存s，说明s已经被其他字符映射，则不更新)
            }
            if (!map2.containsKey(curT)) {
                map2.put(curT, curS); // 构建t->s的映射关系(先入为主，如果已存t，说明t已经被其他字符映射，则不更新)
            }
            // 每次遍历校验更新后的映射关系是否合理
            if (map1.get(curS) != curT || map2.get(curT) != curS) {
                return false;
            }
        }
        // 校验通过
        return true;
    }

}

• 复杂度分析

  • 时间复杂度：O（n）遍历字符串

  • 空间复杂度：O（n）需构建两个map分别存储s->t、t->s的映射关系

🟢1002-查找共用字符

题目内容

给你一个字符串数组 words ，请你找出所有在 words 的每个字符串中都出现的共用字符（包括重复字符），并以数组形式返回。你可以按 任意顺序 返回答案。

示例 1：

输入：words = ["bella","label","roller"]
输出：["e","l","l"]

示例 2：

输入：words = ["cool","lock","cook"]
输出：["c","o"]

2.题解思路

👻方法1：检索法

• 思路分析：
  • ① 统计所有字符串（单词）中的每个字符的出现次数
  • ② 以words[0]的单词为基础进行匹配，判断其单词是否在其余每个字符串中均相应出现
    • 此处单词的选择可以是任意单词，因为每个字符都要出现在每个单词中才算是"共用"，且允许存在重复字符（假设words[0]中有3个a，如果其他单词中每个单词都有3个a则满足共用条件）
    • 针对重复的单词需一一对应，不能重复匹配，因此对于每个单词都选用map存储每个字符的出现次数，如果校验匹配则次数减1

/**
 * 🟢1002 查找共用字符
 */
public class Solution2 {

    public List<String> commonChars(String[] words) {
        int len = words.length;
        /**
         * 选择words[0]中的字符作为判断基础（因为字符要出现在所有字符串，则可任意选择一个字符串）
         * 此处如果选用Set存储就会忽略掉元素重复出现的情况,因此选用map记录每个单词中每个字符的出现次数
         */
        Map<Character, Integer>[] map = new HashMap[len];
        // 记录每个字符串中每个字符的出现次数
        for (int i = 0; i < len; i++) {
            map[i] = new HashMap<>(); // 初始化
            for (char cur : words[i].toCharArray()) {
                map[i].put(cur, map[i].getOrDefault(cur, 0) + 1);
            }
        }

        List<String> res = new ArrayList<>();
        // 以words[0]为基础，校验其他字符串中是否出现一定次数的该字符
        Set<Character> keySet = map[0].keySet();
        for (char cur : keySet) {
            int curCnt = map[0].get(cur); // 获取当前遍历字符出现次数
            while (curCnt-- > 0) { // 对于多次重复出现的字符，需根据出现次数进行处理
                // 校验其他字符串是否均出现该字符
                boolean allMatch = true;
                for (int i = 0; i < len; i++) {
                    boolean match = false;
                    for (Map.Entry<Character, Integer> entry : map[i].entrySet()) {
                        if (entry.getKey() == cur && entry.getValue() > 0) { // 字符匹配且字符可用次数大于0
                            match = true; // 当前匹配，设定标识
                            entry.setValue(entry.getValue() - 1); // 使用次数-1（表示已经校验过的字符不重复校验）
                            break;
                        }
                    }
                    allMatch &= match; // 控制校验状态
                }
                // 如果完全匹配（即所有单词中都出现该字符）
                if (allMatch) {
                    res.add(String.valueOf(cur));
                }
            }
        }
        return res;
    }

    public static void main(String[] args) {
        String[] words = new String[]{"bella", "label", "roller"};
        Solution2 s = new Solution2();
        s.commonChars(words);
    }
}

• 复杂度分析

  • 时间复杂度：O（m×n）n个字符串，每个字符串长度预设为m

  • 空间复杂度：O（n）需构建map存储每个字符串的字符出现次数