skill-11-单调栈
难度说明:🟢简单🟡中等🔴困难
学习资料
学习目标
- 掌握数据结构核心基础
- 借助数据结构完成常见题型
skill-11-单调栈
理论基础
1.核心理论
单调栈的应用场景:通常是一维数组,要寻找任一个元素的右边或者左边第一个比自己大或者小的元素的位置,此时可以联想单调栈的应用。时间复杂度为O(n)
单调栈的本质是空间换时间,用一个栈记录遍历过的元素,在使用单调栈的过程中需要明确几点:
- ① 单调栈中存放的元素是什么? =》下标(如果要获取元素则根据下标获取即可)
- ② 单调栈中的元素是递增还是递减? =》结合场景分析选择**【栈头到栈底的顺序】**递增、递减
- 例如:如果要求一个元素右边第1个更大的元素,则要使用【栈头到栈底的顺序】递增序列,只有递增的时候,栈里要加入一个元素
i的时候,才知道栈顶元素在数组中右面第一个比栈顶元素大的元素是i - 即:如果求一个元素右边第一个更大元素,单调栈就是递增的;如果求一个元素右边第一个更小元素,单调栈就是递减的
- 例如:如果要求一个元素右边第1个更大的元素,则要使用【栈头到栈底的顺序】递增序列,只有递增的时候,栈里要加入一个元素
- ③ 单调栈的判断:根据遍历元素与栈顶元素的比较进行分析(确保栈内元素的顺序维持)
- 遍历元素
T[i]小于 栈顶元素T[s.top()] - 遍历元素
T[i]等于 栈顶元素T[s.top()] - 遍历元素
T[i]大于 栈顶元素T[s.top()]
- 遍历元素
2.技巧总结
常见题型
- 739-每日温度:单调栈(栈顶到栈底:递增)
- 496-下一个更大元素I
- 暴力搜索:先找出
nums1[i]==nums2[j]然后基于j进一步找下一个更大的元素 - 哈希表 + 单调栈(栈顶到栈底:递增):借助map存储
nums1[],以nums2[]为基础遍历,找到每个nums2[j]对应的下一个更大的元素,如果nums2[j]在map中存在则填充
- 暴力搜索:先找出
- 503-下一个更大元素II
- 平展循环数组 + 单调栈:构建 2 × len 的原数组(将循环数组平展后为两个原数组拼接成的新数组),对新数组进行单调栈处理
- 两次循环 + 单调栈:在单数组的单调栈处理的思路上,遍历两次数组,将原
nums[i]概念调整为nums[i%size]
- 042-接雨水
- 动态规划(纵向维度):分别计算左侧最大前缀、右侧最大前缀,然后基于
min{leftMax,rightMax} - height[i]得到每个柱子所接雨水量的累加和 - 单调栈(横向维度):构建【栈顶到栈底:单调递增】的单调栈,根据遍历元素与栈顶元素的不同情况讨论,主要是计算
v = w * h的值(计算凹槽面积)height[i]<height[st.top()]:元素入栈height[i]=height[st.top()]:需更新栈顶元素(先弹出栈顶元素后入栈),遇到相同高度的柱子需要使用右边的柱子来计算宽度height[i]>height[st.top()]:如果当前遍历元素高度大于栈顶元素高度,此时出现凹槽,需要计算雨水量- 取出栈顶元素(将栈顶元素弹出)得到凹槽底部索引
mid;紧接其后的栈顶元素即为【凹槽左边高度】(索引为st.top());当前遍历元素为【凹槽右边高度】,其索引为i - 雨水量:
- 凹槽高度:min{凹槽左边高度,凹槽右边高度}-凹槽底部高度 =》
int h=min{height[st.top()],height[i]} - height[mid] - 凹槽宽度:【凹槽右边下标】-【凹槽左边下标】-1 (只求中间宽度) =》
int w = i - st.top() - 1 - 雨水体积:
int v = h * w
- 凹槽高度:min{凹槽左边高度,凹槽右边高度}-凹槽底部高度 =》
- 取出栈顶元素(将栈顶元素弹出)得到凹槽底部索引
- 动态规划(纵向维度):分别计算左侧最大前缀、右侧最大前缀,然后基于
- 084-柱状图中的最大矩形
- 单调栈:思路和接雨水大同小异,此处需注意单调栈的维护顺序(栈顶到栈底:单调递减),以及对特例情况的处理(对原
heights数组首尾补0,基于新数组进行单调栈处理,用于处理连续单调递减或连续单调递增的情况)- 遍历元素
h[i]与栈顶元素h[top]:h[i]>h[top]:入栈h[i]=h[top]:入栈h[i]<h[top]: 依次弹出元素(直至h[i]<h[top]不满足),以弹出的元素为基础计算所能构建的最大矩形:- 分别得到高度(第1个栈顶元素索引指向)、左边界(第2个栈顶元素索引指向)、右边界(当前遍历元素索引i) =》
area = w * h = (right-left-1) * h[mid]
- 分别得到高度(第1个栈顶元素索引指向)、左边界(第2个栈顶元素索引指向)、右边界(当前遍历元素索引i) =》
- 遍历元素
- 单调栈:思路和接雨水大同小异,此处需注意单调栈的维护顺序(栈顶到栈底:单调递减),以及对特例情况的处理(对原
常见题型
🟡739-每日温度
1.题目内容
给定一个整数数组 temperatures ,表示每天的温度,返回一个数组 answer ,其中 answer[i] 是指对于第 i 天,下一个更高温度出现在几天后。如果气温在这之后都不会升高,请在该位置用 0 来代替。
示例 1:
输入: temperatures = [73,74,75,71,69,72,76,73]
输出: [1,1,4,2,1,1,0,0]
示例 2:
输入: temperatures = [30,40,50,60]
输出: [1,1,1,0]
示例 3:
输入: temperatures = [30,60,90]
输出: [1,1,0]
2.题解思路
👻方法1:双层循环检索(❌超时)
- 思路分析:
- 双层循环遍历:外层确定
i位置,内层确定j(下一个比i位置温度高的位置,找到则设置answer[i]并退出内层循环,找不到则默认为0)
- 双层循环遍历:外层确定
/**
* 739 每日温度
*/
public class Solution1 {
// 双层循环检索:外层遍历i,内层寻找下一个比i位置元素大的元素(不存在则为0)
public int[] dailyTemperatures(int[] temperatures) {
// 定义数组存储温度变化情况
int[] answer = new int[temperatures.length];
// 双层循环遍历
for(int i=0;i<temperatures.length;i++){ // 外层确定i位置
for(int j=i+1;j<temperatures.length;j++){ // 内层寻找比temperatures[i]大的元素,如果找不到则answer[i]为0
if(temperatures[j]>temperatures[i]){
answer[i]=j-i;
break; // 找到了下一个更高的温度,跳出内层循环
}
}
}
// 返回结果
return answer;
}
}
复杂度分析
时间复杂度:O(n2)
空间复杂度:O(n)
👻方法2:单调栈
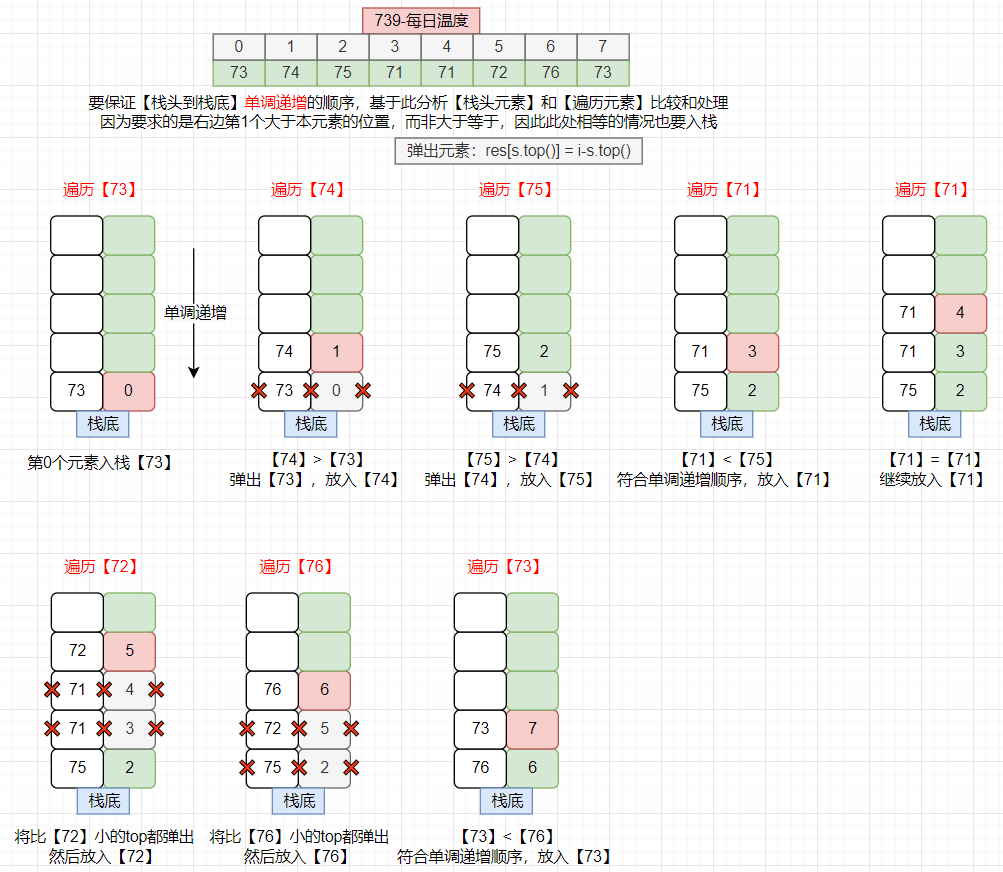
单调栈思路分析
- 单调栈存什么?=》下标
- 单调栈的顺序(栈头到栈底)?=》递增(此处是检索右侧第一个比当前元素大的元素,确保当前遍历元素
i为栈顶元素右侧的第1个比它大的元素) - 单调栈的判断?=》根据当前遍历元素
t[i]和栈顶元素t[top]进行比较分析t[i]<t[top]:符合【栈头到栈底单调递增】,直接入栈t[i]=t[top]:此处求的是比它大的元素,对于相等的情况处理,直接入栈t[i]>t[top]:不符合【栈头到栈底单调递增】,要依次遍历分别将t[top]<t[i]的top元素弹出,并记录res[top]=i-top(因为此时当前遍历元素位置i就是表示比栈顶top元素大的第1个元素)- 综述:当栈不为空,则依次校验栈顶元素topVal与当前遍历元素curVal,将满足
topVal<=curVal(说明找到了比当前栈顶元素大的值)栈顶元素都弹出来(while),最后再将curVal对应索引入栈
/**
* 739 每日温度
*/
public class Solution2 {
// 双层循环检索:外层遍历i,内层寻找下一个比i位置元素大的元素(不存在则为0)
public int[] dailyTemperatures(int[] t) { // temperatures
// 定义数组存储温度变化情况
int[] res = new int[t.length];
// 构建辅助栈用作单调栈(从栈头到栈底是单调递增:求右边第一个大的元素)
Stack<Integer> st = new Stack<>();
st.push(0); // 初始化栈(第1个元素入栈)
/**
* 单调栈处理:遍历元素 t[i] t[st.top()]
* ① t[i] < t[st.peek()] 符合单调递增顺序,入栈
* ② t[i] = t[st.peek()] 求大于当前元素的情况,此处等于也正常入栈
* ③ t[i] > t[st.peek()] 将栈顶元素小于t[i]的元素依次弹出(并更新:res[st.top()]=i-st.top()),并将i位置元素入栈
*/
for (int i = 1; i < t.length; i++) {
if (t[i] < t[st.peek()]) {
st.push(i); // 下标入栈
} else if (t[i] == t[st.peek()]) {
st.push(i); // 下标入栈
} else {
// 将栈顶元素小于t[i]的元素依次弹出
while (!st.isEmpty() && t[i] > t[st.peek()]) { // 栈不为空判断
res[st.peek()] = i - st.peek();
st.pop();
}
// 将当前元素入栈
st.push(i);
}
}
// 返回结果
return res;
}
}
复杂度分析
时间复杂度:O(n) (单调栈:时间换空间的应用场景)
空间复杂度:O(n)需要构建辅助栈存储已遍历元素
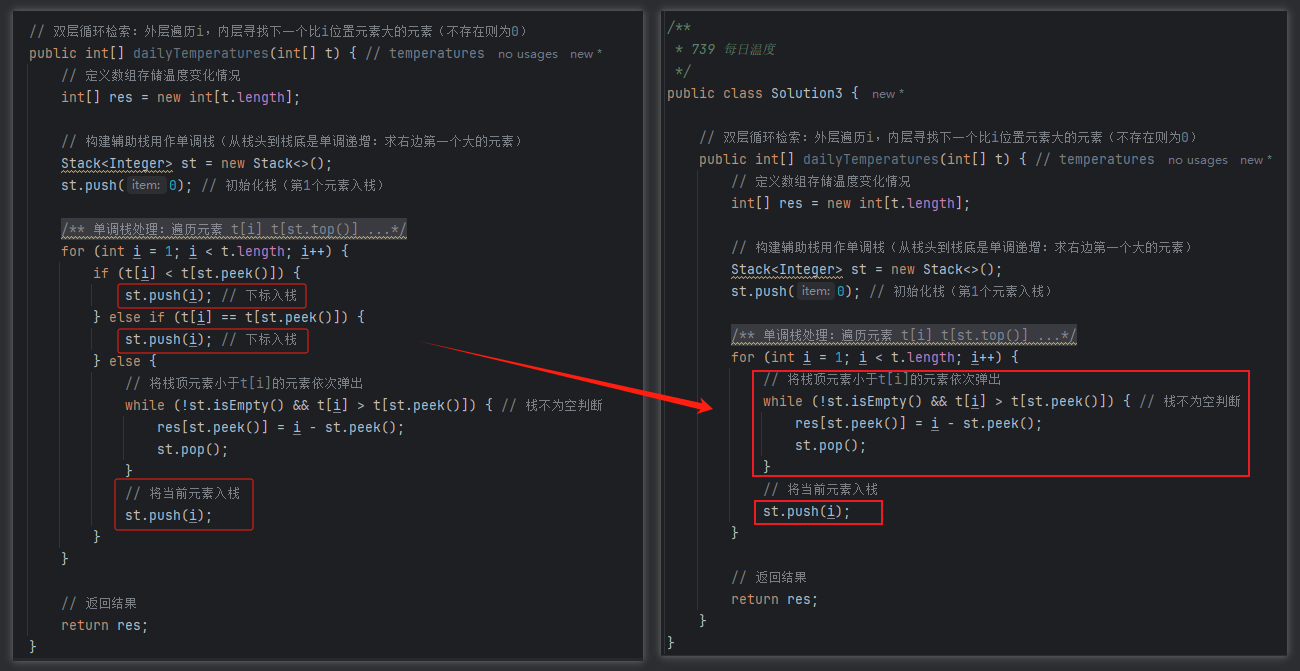
单调栈-简化版本
可以看到每一种情况最终都是要将当前遍历元素入栈,唯一的不同在于根据单调栈递增的顺序对栈顶元素进行处理,此处为了保证单调栈【栈头到栈底递增的顺序】,遇到t[top]<t[i]的情况,要将所有小于t[i]的栈顶元素弹出(并填充res[top]=i-top,此时i即为第1个大于top位置元素的位置,弹出的同时处理ans即可)
🟢496-下一个更大元素I
1.题目内容
nums1 中数字 x 的 下一个更大元素 是指 x 在 nums2 中对应位置 右侧 的 第一个 比 x 大的元素。
给你两个 没有重复元素 的数组 nums1 和 nums2 ,下标从 0 开始计数,其中nums1 是 nums2 的子集。
对于每个 0 <= i < nums1.length ,找出满足 nums1[i] == nums2[j] 的下标 j ,并且在 nums2 确定 nums2[j] 的 下一个更大元素 。如果不存在下一个更大元素,那么本次查询的答案是 -1 。
返回一个长度为 nums1.length 的数组 ans 作为答案,满足 ans[i] 是如上所述的 下一个更大元素 。

2.题解思路
👻方法1:嵌套循环
- 思路分析:
- 外层循环遍历
nums1,内层循环先找到nums1[i]==nums2[j]的j,然后在nums2中寻找第1个比nums1[i]要大的元素,不存在则置为-1
- 外层循环遍历
/**
* 496 下一个更大的元素I
*/
public class Solution1 {
// 暴力循环
public int[] nextGreaterElement(int[] nums1, int[] nums2) {
int len1 = nums1.length, len2 = nums2.length;
// 定义结果集
int[] res = new int[len1];
Arrays.fill(res, -1); // 默认置为-1
// 外层循环确定nums1的每个元素,内存循环寻找在nums2中比nums1要大的第1个元素
for (int i = 0; i < len1; i++) {
for (int j = 0; j < len2; j++) {
if (nums1[i] == nums2[j]) { // 因为题中给出数组中不存在重复元素,所以可以确保找到一个唯一的内容
for (int k = j + 1; k < len2; k++) {
if (nums1[i] < nums2[k]) {
res[i] = nums2[k]; // 记录下一个更大的元素
break; // 已经寻找到第一个大的元素,跳出内层循环,继续下一个i位置遍历
}
}
}
}
}
// 返回结果
return res;
}
}
/**
* 496 下一个更大的元素I
*/
public class Solution2 {
// 暴力循环
public int[] nextGreaterElement(int[] nums1, int[] nums2) {
int len1 = nums1.length, len2 = nums2.length;
// 定义结果集
int[] res = new int[len1];
Arrays.fill(res, -1); // 默认置为-1
// 外层循环确定nums1的每个元素,内存循环寻找在nums2中比nums1要大的第1个元素
for (int i = 0; i < len1; i++) {
// 先找到nums1[i]==nums2[j]的位置
int j = 0;
while (nums1[i] != nums2[j] && j < len2) {
j++;
}
// 从j+1位置开始遍历,寻找第一个比nums1[i](nums2[j])大的元素
for (int k = j + 1; k < len2; k++) {
if (nums1[i] < nums2[k]) {
res[i] = nums2[k]; // 记录下一个更大的元素
break; // 已经寻找到第一个大的元素,跳出内层循环,继续下一个i位置遍历
}
}
}
// 返回结果
return res;
}
}
复杂度分析
时间复杂度:O(n2)
空间复杂度:O(n)存储结果集
👻方法2:单调栈
- 思路分析:
- 下一个更大元素的查找前提是
nums1[i]==nums2[j],因此拆分步骤实现:- 借助
Map<item,index>存储num1,可以在nums2遍历过程中快速判断元素是否在map(nums1)中存在 - 随后将
nums2[]数组的遍历使用单调栈处理寻找下一个更大的数,如果找到这个数就相应填充res(元素索引出栈的时候进行判断)
- 借助
- 下一个更大元素的查找前提是
/**
* 496 下一个更大的元素I
*/
public class Solution3 {
// 单调栈
public int[] nextGreaterElement(int[] nums1, int[] nums2) {
int len1 = nums1.length, len2 = nums2.length;
// 定义结果集
int[] res = new int[len1];
Arrays.fill(res, -1); // 默认置为-1
// 使用map存储nums1
Map<Integer, Integer> map = new HashMap<>();
for (int i = 0; i < len1; i++) {
map.put(nums1[i], i);
}
// 使用单调栈处理nums2寻找下一个更大的数
Stack<Integer> st = new Stack<>();
st.push(0); // 初始化第0个元素索引入栈
for (int i = 1; i < len2; i++) {
// 判断nums2[i]与栈顶元素的大小(栈顶到栈底:递增序列)
if (nums2[i] <= nums2[st.peek()]) {
st.push(i); // 元素入栈
} else {
while (!st.isEmpty() && nums2[i] > nums2[st.peek()]) {
// 弹出元素并记录(判断当前栈顶索引指向元素是否在map中出现)
if (map.containsKey(nums2[st.peek()])) {
// 记录其下一个更大的元素
res[map.get(nums2[st.peek()])] = nums2[i];
}
st.pop(); // 弹出栈顶元素
}
st.push(i);// 元素入栈
}
}
// 返回结果
return res;
}
}
- 复杂度分析
时间复杂度:O(m+n),m是nums1数组长度、n是nums2数组长度,需要分别遍历两个数组
空间复杂度:O(m)用于存储哈希表
🟡503-下一个更大元素II
1.题目内容
给定一个循环数组 nums ( nums[nums.length - 1] 的下一个元素是 nums[0] ),返回 nums 中每个元素的 下一个更大元素 。
数字 x 的 下一个更大的元素 是按数组遍历顺序,这个数字之后的第一个比它更大的数,这意味着你应该循环地搜索它的下一个更大的数。如果不存在,则输出 -1 。
示例 1:
输入: nums = [1,2,1]
输出: [2,-1,2]
解释: 第一个 1 的下一个更大的数是 2;
数字 2 找不到下一个更大的数;
第二个 1 的下一个最大的数需要循环搜索,结果也是 2。
示例 2:
输入: nums = [1,2,3,4,3]
输出: [2,3,4,-1,4]
2.题解思路
👻方法1:平展循环数组 + 单调栈
- 思路分析:
- (1)构建一个
2*len的数组,将循环数组平展成2个原数组拼接后的新数组newNums - (2)随后基于
newNums使用单调栈进行遍历(只需要遍历一半的元素),寻找其可能的下一个更大的元素即可
- (1)构建一个
/**
* 503 下一个更大元素II
*/
public class Solution1 {
// 平展循环数组 + 单调栈思路
public int[] nextGreaterElements(int[] nums) {
int len = nums.length;
// 定义结果集
int[] res = new int[2 * len];
Arrays.fill(res, -1);
// 将循环数组平展成一个新数组
int[] newNums = new int[2 * len];
System.arraycopy(nums, 0, newNums, 0, len); // 数组复制
System.arraycopy(nums, 0, newNums, len, len); // 数组复制
// 基于单调栈,对新数组newNums进行遍历、封装
Stack<Integer> st = new Stack<>();
st.push(0); // 初始化
for (int i = 1; i < newNums.length; i++) {
// 简化版本单调栈处理
while (!st.isEmpty() && newNums[i] > newNums[st.peek()]) {
res[st.peek()] = newNums[i]; // 记录栈顶元素的下一个更大元素
st.pop(); // 栈顶元素出栈
}
st.push(i); // 入栈处理
}
// 返回结果集
return Arrays.copyOfRange(res, 0, len);
}
}
复杂度分析
- 时间复杂度:O(2 × n)需遍历两次数组,还需考虑数组复制的时间、空间消耗
空间复杂度:O(3 × n)平展数组、栈等空间占用
👻方法2:2次循环遍历 + 单调栈
- 思路分析:
- (1)不用平展循环数组,直接两次循环遍历进行单调栈处理,只需要将原有的
nums[i]概念切换为nums[i%size](本质和平展数组概念类似,只不过此处是循环多次,巧用下标取余) - (2)基于
nums使用单调栈进行遍历(只需要遍历一半的元素),寻找其可能的下一个更大的元素即可
- (1)不用平展循环数组,直接两次循环遍历进行单调栈处理,只需要将原有的
/**
* 503 下一个更大元素II
*/
public class Solution2 {
// 2次循环遍历 + 单调栈
public int[] nextGreaterElements(int[] nums) {
int len = nums.length;
// 定义结果集
int[] res = new int[len];
Arrays.fill(res, -1);
// 基于单调栈,对新数组newNums进行遍历、封装
Stack<Integer> st = new Stack<>();
st.push(0); // 初始化
for (int i = 1; i < 2 * len; i++) {
// 简化版本单调栈处理
while (!st.isEmpty() && nums[i % len] > nums[st.peek()]) {
res[st.peek()] = nums[i % len]; // 记录栈顶元素的下一个更大元素
st.pop(); // 栈顶元素出栈
}
st.push(i % len); // 入栈处理
}
// 返回结果集
return res;
}
}
复杂度分析
时间复杂度:O(2×n)
空间复杂度:O(n)辅助栈
🔴042-接雨水
1.题目内容

2.题解思路
👻方法1:动态规划(列维度)
思路分析:按照列维度计算
对于下标
i,下雨后水能到达的最大高度等于下标i两边的最大高度的最小值,下标i处能接的雨水量等于下标i处的水能到达的最大高度减去height[i]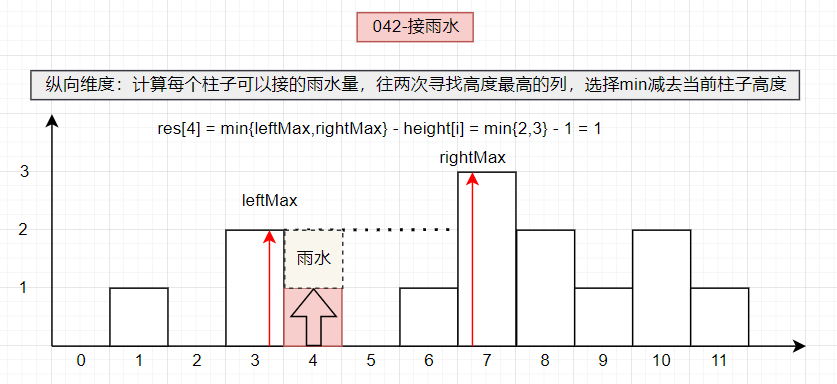
分别求得数组元素的对应位置的最大前缀和最大后缀,随后遍历取得两者的最小值
min{leftMax,rightMax}减去柱状高度(即元素)所得的累加和即为接的雨水总量- 最大前缀(正序遍历):
leftMax[i] = Math.max(leftMax[i - 1], height[i]);(i∈[1,len-1]) - 最大后缀(逆序遍历):
rightMax[j] = Math.max(rightMax[j + 1], height[j]);(j∈[0,len-2]) - 每个下标位置可以接到的水量:
min{leftMax[i],rightMax[i]}-height[i],通过累加每个下标位置的接水量得到总雨水量
- 最大前缀(正序遍历):
/**
* 042 接雨水
*/
public class Solution1 {
public int trap(int[] height) {
int len = height.length;
// 1.求数组元素的最大前缀
int[] leftMax = new int[len];
leftMax[0] = height[0];
for (int i = 1; i < len; i++) {
leftMax[i] = Math.max(leftMax[i - 1], height[i]);
}
System.out.println("leftMax[]:");
PrintDPUtil.print(leftMax);
// 2.求数组元素的最大后缀
int[] rightMax = new int[len];
rightMax[len - 1] = height[len - 1];
for (int j = len - 2; j >= 0; j--) {
rightMax[j] = Math.max(rightMax[j + 1], height[j]);
}
System.out.println("rightMax[]:");
PrintDPUtil.print(rightMax);
// 3.求雨水总量
int res = 0;
for (int i = 0; i < len; i++) {
res += Math.min(leftMax[i], rightMax[i]) - height[i];
}
// 返回结果
return res;
}
public static void main(String[] args) {
int[] height = new int[]{0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1};
Solution1 solution1 = new Solution1();
System.out.println("res:" + solution1.trap(height));
}
}
复杂度分析
时间复杂度:O(3×n)(即O(n))需遍历3次数组填充数据:第1次遍历求最大前缀、第2次遍历求最大后缀、第三次遍历求接雨水总量
空间复杂度:O(2×n)(即O(n))定义两个数组分别存储元素的最大前缀
leftMax[]、最大后缀rightMax[]
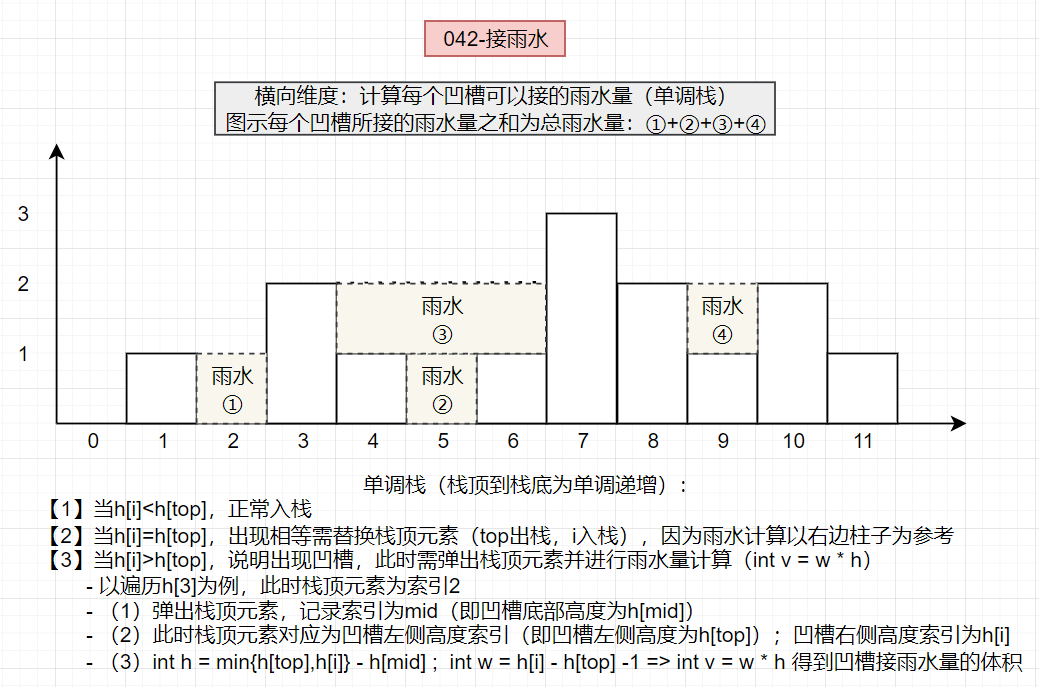
👻方法2:单调栈(行维度)
思路分析:单调栈是按照行方向来计算雨水
- 单调栈存储什么?=》下标索引
i - 单调栈的顺序?=》栈顶到栈底(单调递增:从小到大)
- 单调栈的判断:遍历元素
height[i]柱子高度与栈顶元素height[st.top()]的比较?height[i]<height[st.top()]:元素入栈height[i]=height[st.top()]:需更新栈顶元素(先弹出栈顶元素后入栈),遇到相同高度的柱子需要使用右边的柱子来计算宽度height[i]>height[st.top()]:如果当前遍历元素高度大于栈顶元素高度,此时出现凹槽,需要计算雨水量- 取出栈顶元素(将栈顶元素弹出)得到凹槽底部索引
mid - 紧接获取其后的栈顶元素即为【凹槽左边高度】,其索引为
st.top() - 当前遍历元素为【凹槽右边高度】,其索引为
i - 雨水量:
- 凹槽高度:min{凹槽左边高度,凹槽右边高度}-凹槽底部高度 =》
int h=min{height[st.top()],height[i]} - height[mid] - 凹槽宽度:【凹槽右边下标】-【凹槽左边下标】-1 (只求中间宽度) =》
int w = i - st.top() - 1 - 雨水体积:
int v = h * w
- 凹槽高度:min{凹槽左边高度,凹槽右边高度}-凹槽底部高度 =》
- 取出栈顶元素(将栈顶元素弹出)得到凹槽底部索引
- 单调栈存储什么?=》下标索引
易错点分析:
① 此处需注意
stack的变化和值的校验,避免stack变化对校验值带来的影响(例如stack已经弹出元素,但前面定义了变量接收原来的栈顶元素,变成校验的还是原来的内容)② 需理解元素的处理和NPE校验
如何确定凹槽?(当出现
topVal<curVal时,则不断处理凹槽)- 取出第1个栈顶元素为底部(
midIdx) - 获取第2个栈顶元素为左柱子(
leftIdx)(该值可能会作为其他凹槽的底部,因此暂不弹出) - 当前遍历元素则为右柱子(
rightIdx)
- 取出第1个栈顶元素为底部(
凹槽容量如何计算?
- w(宽度):
w=rightIdx-leftIdx-1 - h(高度):
h=min{h[leftIdx],h[rightIdx]} - h[midIdx](左右柱子中选择较低的柱子为凹槽的最高高度,中间柱子的高度为凹槽底部,得到凹槽高度为max{L,R}-M)
- w(宽度):
/**
* 042 接雨水
*/
public class Solution2 {
// 单调栈:行维度(计算凹槽体积容量:v = w * h)
public int trap(int[] height) {
// 构建辅助栈
Stack<Integer> st = new Stack<>();
st.push(0);
int res = 0;
// 遍历元素,计算凹槽接水量
for (int i = 1; i < height.length; i++) {
// 单调栈(栈顶到栈底:单调递增(从小到大))
if (height[i] < height[st.peek()]) {
// 符合单调递增,直接入栈
st.push(i);
} else if (height[i] == height[st.peek()]) {
// 如果height[i]=height[top],雨水量的计算需要参考右边的柱子,此处遇到相等的情况需要将原来的弹出
st.pop();
st.push(i);
} else {
// 如果height[i]>height[top],依次弹出栈顶元素并计算雨水量
while (!st.isEmpty() && height[i] > height[st.peek()]) {
int mid = st.pop();
if (!st.isEmpty()) { // NPE 处理
int h = Math.min(height[i], height[st.peek()]) - height[mid]; // 高度计算
int w = i - st.peek() - 1; // 宽度计算
res += h * w; // 容量计算并累加结果
}
}
st.push(i);
}
}
// 返回结果
return res;
}
public static void main(String[] args) {
int[] height = new int[]{0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1};
Solution2 solution1 = new Solution2();
System.out.println("res:" + solution1.trap(height));
}
}
复杂度分析
- 时间复杂度:O(n)n 为柱子个数,需遍历一遍数组元素
- 空间复杂度:O(n)借助辅助栈存储已遍历元素,基于单调栈思路实现
🔴084-柱状图中最大的矩形
1.题目内容
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
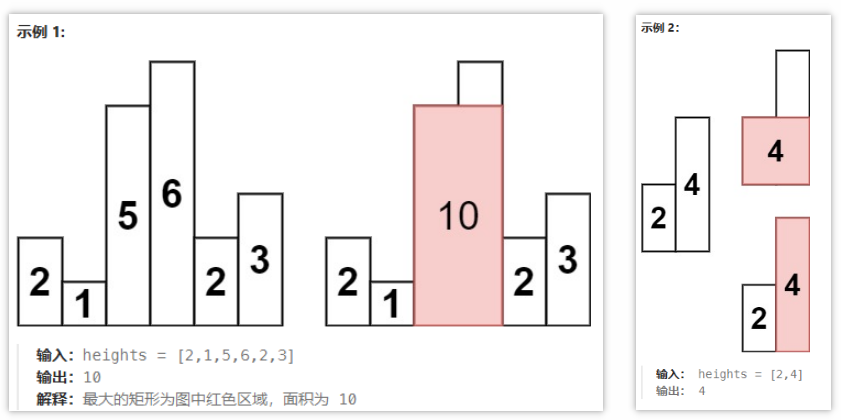
2.题解思路
👻方法1:单调栈
- 思路分析(和接雨水的单调栈思路大同小异,注意此处单调栈的元素顺序)
- (1)单调栈中存储内容 =》索引
- (2)单调栈元素顺序 =》栈顶到栈底:降序(从大到小)
- 因为此处是为了尽可能构成更大的矩形,让较大的高度入栈
- (3)遍历元素
h[i]与栈顶元素h[top]:h[i]>h[top]:入栈h[i]=h[top]:入栈h[i]<h[top]: 依次弹出元素(直至h[i]<h[top]不满足),以弹出的元素为基础计算所能构建的最大矩形:- 错误思路:
min{h[x]} * n(弹出元素中选择最小的高度乘以弹出个数得到矩形面积) (以1 5 6为例,明显不符合) - 正确思路:分别得到高度(第1个栈顶元素索引指向)、左边界(第2个栈顶元素索引指向)、右边界(当前遍历元素索引i) =》
area = w * h = (right-left-1) * h[mid]- 取出第1个栈顶元素为高度、获取第2个栈顶元素为左边界、当前遍历元素位置为右边界
- 错误思路:
- (4)特例情况讨论:需对原
heights数组进行首尾补0,因为考虑到连续单调递减或连续单调递增的情况,如果不补0则无法处理整个数组连续单调的特例情况:- 以
2 4为例,如果尾部没有补0,则遍历到4这个位置就会把4这个位置的最大面积讨论给截断了 - 以
3 2为例,如果头部没有补0,则会把3作为mid(高度讨论)的情况给忽略掉(且需处理NPE)
- 以
/**
* 084 柱状图中的最大的矩形
*/
public class Solution1 {
/**
* 单调栈思路
* (1)单调栈中存储内容 =》索引
* (2)单调栈元素顺序 =》栈顶到栈底:降序(从大到小)
* (3)遍历元素h[i]与栈顶元素h[top]:
* - h[i]>h[top]:入栈
* - h[i]=h[top]:入栈
* - h[i]<h[top]: 依次弹出元素(直至h[i]<h[top]不满足),以弹出的元素为基础计算所能构建的最大矩形:
* - 错误思路:min{h[x]} * n (弹出元素中选择最小的高度乘以弹出个数得到矩形面积) (以1 5 6为例)
* - 正确思路:分别得到高度(第1个栈顶元素索引指向)、左边界(第2个栈顶元素索引指向)、右边界(当前遍历元素索引i) =》area = w * h = (right-left-1) * h[mid]
*/
public int largestRectangleArea(int[] heights) {
int len = heights.length;
// 构建辅助栈
Stack<Integer> st = new Stack<>();
st.push(0); // 初始化
// 定义最大面积
int maxArea = 0;
// 构建新数组首尾补充0,用于处理heights连续单调递减或连续单调递增的情况(如果不补充0,则出现连续递增的话得到结果为0不符合特例要求)
int[] newHeights = new int[len + 2];
System.arraycopy(heights, 0, newHeights, 1, len);
newHeights[0] = 0;
newHeights[newHeights.length - 1] = 0;
// 遍历元素(对新数组进行处理)
for (int i = 1; i < newHeights.length; i++) {
if (newHeights[i] >= newHeights[st.peek()]) {
st.push(i);
} else {
while (!st.isEmpty() && newHeights[i] < newHeights[st.peek()]) {
int mid = st.pop(); // 弹出第一个栈顶元素作为高度(讨论每个弹出元素作为mid(高度)时的面积分析)
int left = st.peek(); // 其左边界为当前栈顶元素所在索引
int right = i; // 其右边界为当前遍历位置i
int w = right - left - 1; // 计算宽度
int h = newHeights[mid]; // 计算高度
maxArea = Math.max(maxArea, w * h); // 更新最大面积
}
// 将当前元素入栈
st.push(i);
}
}
// 返回结果
return maxArea;
}
public static void main(String[] args) {
Solution1 solution1 = new Solution1();
int[] heights1 = new int[]{2, 1, 5, 6, 2, 3};
int[] heights2 = new int[]{2, 4}; // 连续单调递增
int[] heights3 = new int[]{4, 3}; // 连续单调递减
solution1.largestRectangleArea(heights1);
solution1.largestRectangleArea(heights2);
solution1.largestRectangleArea(heights3);
}
}
// output: 10 4 6
复杂度分析
时间复杂度:O(n) 遍历数组元素
空间复杂度:O(n)构建辅助栈用作单调栈思路处理
