skill-04-字符串
难度说明:🟢简单🟡中等🔴困难
学习资料
学习目标
- 掌握数据结构核心基础
- 借助数据结构完成常见题型
skill-04-字符串
理论基础
1.核心理论
主要考察字符串操作基础,打基础的时候不要太依赖于库函数。如果一些算法核心过于依赖库函数(一行代码解决),那就失去了考察的意义
2.技巧总结
- 库函数的使用:尽量避免核心代码完全依赖库函数(思考如果自己去实现这个逻辑要如何入手),考察对字符串的操作能力
- 双指针法:双指针法在字符串处理中是比较常见的(字符串反转(反转系列)、替换空格等)
- KMP:KMP 算法的应用(
strStr()、重复的子字符串算法实现)
常见题型
🟢344-反转字符串
1.题目内容
编写一个函数,其作用是将输入的字符串反转过来。输入字符串以字符数组 s 的形式给出。
不要给另外的数组分配额外的空间,你必须**原地修改输入数组**、使用 O(1) 的额外空间解决这一问题。
示例 1:
输入:s = ["h","e","l","l","o"]
输出:["o","l","l","e","h"]
示例 2:
输入:s = ["H","a","n","n","a","h"]
输出:["h","a","n","n","a","H"]
2.题解思路
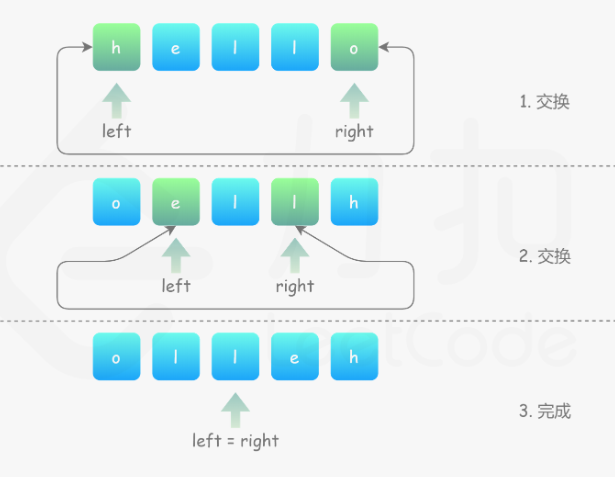
👻方法1:双指针+交换(原地算法)
- 思路分析:定义双指针,分别从头尾向中间靠拢,依次交换两边的元素
left<right的设定- 如果字符数组
s为奇数:最中间的没必要交换 - 如果字符数组
s为偶数:可以满足交换
- 如果字符数组
// 思路1:双指针(元素交换)原地修改且空间复杂度满足O(1)
public void reverseString(char[] s) {
int left = 0,right = s.length-1;
while(left<right){
// 交换左右元素
char temp = s[left];
s[left] = s[right];
s[right] = temp;
// 交换完毕,双指针向中间靠拢继续交换下一组元素
left++;
right--;
}
}
复杂度分析
时间复杂度:O(n)n 为数组长度
空间复杂度:O(1)原地算法
另一种写法:数组遍历的双指针写法
// 思路1:双指针(元素交换)原地修改且空间复杂度满足O(1)
public void reverseString(char[] s) {
// 分别从头尾遍历数组元素,依次交换
for (int start = 0, end = s.length - 1; start < end; start++, end--) {
// 交换两头的元素
char temp = s[start];
s[start] = s[end];
s[end] = temp;
}
}
👻方法2:辅助数组反转❌(不满足原地和O(1)要求)
- 思路分析:构建辅助数组(或者集合),逆序遍历字符数组,然后进行封装(仅作为思路参考,不满足原地修改和O(1)要求)
// 思路2:O(n) 辅助数组反转
public void reverseString(char[] s) {
char[] reverseArr = new char[s.length];
int cur = 0;// 定义新数组游标指针
for(int i=s.length-1;i>=0;i--){
reverseArr[cur++] = s[i];
}
// 重新封装数组
for(int i=0;i<reverseArr.length;i++){
s[i] = reverseArr[i];
}
}
复杂度分析
时间复杂度:O(n) 遍历原字符数组,如果要满足原地要将反转后的数组元素重新封装到原字符数组
空间复杂度:O(n)
🟢541-反转字符串II
1.题目内容
给定一个字符串 s 和一个整数 k,从字符串开头算起,每计数至 2k 个字符,就反转这 2k 字符中的前 k 个字符。
- 如果剩余字符少于
k个,则将剩余字符全部反转。 - 如果剩余字符小于
2k但大于或等于k个,则反转前k个字符,其余字符保持原样
示例 1:
输入:s = "abcdefg", k = 2
输出:"bacdfeg"
示例 2:
输入:s = "abcd", k = 2
输出:"bacd"
2.题解思路
👻方法1:局部反转(限定反转范围)
核心:局部反转(步长2k,反转范围[start,end]=[i,min{i+k-1,len-1}])
- 思路分析:分析反转规律,可以从题意中拆解局部反转的思路,确定要反转的范围然后依次反转即可(此处将字符串转化为字符数组便于处理)
- 反转范围(
0,k-1,2k,3k-1......i,i+k-1)- 步长:2k(
for循环定位每一个反转的起点,然后敲定反转范围终点) - 范围:2k范围内:
[i,i+k-1],2k范围外(看remind与K的比较):remind>=k(i,i+k-1);remind<k(i,len-1)
- 步长:2k(
- 反转:局部反转的思路,指定反转区域
[start,end]对数组进行原地的局部反转,不需要额外截断数组进行反转、拼接
- 反转范围(
/**
* 541 反转字符串II
*/
public class Solution2 {
// 思路:根据限定条件反转字符串(转化为字符数组处理)
public String reverseStr(String s, int k) {
// 将字符串转化为字符数组
char[] arr = s.toCharArray();
// 判断s与2k的关系,确定反转规则
int len = s.length();
// 反转指定索引范围的元素(0-k,2k-3k,......)
for (int i = 0; i < len; i += 2 * k) {
/**
* 此处可以拆分为两部分:一部分是2k范围内的数据(k>=0),一部分是2k范围外的数据
* 两种场景的起点start其实都是一样的(0、2k、4k),而终点的取值则要看数组元素的长度大小
* - 对于2k范围内的取值,end=i+k-1
* - 对于2k范围外的取值,end有两种取值情况(取决于超出2k范围的部分remind的长度)
* - remind >= k , end = i+k-1 剩余子串长度超出k
* - remind < k , end = len-1 剩余子串长度不足K
* - 上述讨论均覆盖了k=0的情况,则可进一步整合这几种情况:
* - 起点相同,步长均为2K,终点则是选择 Math.min(i + k, len) - 1)
*/
reverseArr(arr, i, Math.min(i + k, len) - 1);
}
// 返回结果
return new String(arr);
}
// 反转指定索引范围的数组([left,right])
public void reverseArr(char[] chs, int start, int end) {
// 原地反转指定索引位置范围的数组元素,避免重复截取数组的开销(Arrays.copyOfRange(arr, start,end);)
// for (int start = 0, end = chs.length - 1; start < end; start++, end--) {
while (start < end) {
// 交换元素
char temp = chs[start];
chs[start] = chs[end];
chs[end] = temp;
// 指针移动
start++;
end--;
}
}
}
复杂度分析
时间复杂度:O(n)n为字符串长度
空间复杂度:O(n)需借助字符数组辅助反转
/**
* 🟢 541 反转字符串II
*/
public class Solution541_01 {
/**
* 局部反转思路(限定反转范围,每一个轮次的起点终点)
* 反转轮次:0,2k,4k,6k....(对于每个轮次,超出2k范围,看最终剩余的元素数量与k的关系,不足k全部反转,足k则反转前K)
* 反转的起始范围:[i,end],此处end有两种情况讨论:
* - ①在2k*n轮次范围限定中:[i,i+k-1]
* - ②在2k*n轮次范围之后(剩余的字符):end=min{i+k-1,len-1}
* - 2.a 如果剩余字符个数>=k:[i,i+k-1]
* - 2.b 如果剩余字符个数<k:[i,len-1](考虑数组长度限定,此处是将剩余所有字符反转)
*/
public String reverseStr(String s, int k) {
int len = s.length();
char[] arr = s.toCharArray();
// 限定反转范围,局部反转字符串(将字符串转化为字符数组进行处理)
for (int i = 0; i < len; i += 2 * k) { // 处理每一个轮次的字符串反转
reverse(arr, i, Math.min(i + k - 1, len - 1));
}
// 将反转后的字符数组还原成字符串
return new String(arr);
}
/**
* 局部反转字符数组(原地反转)
*/
public void reverse(char[] arr, int start, int end) {
while (start <= end) {
// 反转
char temp = arr[start];
arr[start] = arr[end];
arr[end] = temp;
// 指针移动
start++;
end--;
}
}
}
🟢KMW054-替换数字
1.题目内容
给定一个字符串 s,它包含小写字母和数字字符,请编写一个函数,将字符串中的字母字符保持不变,而将每个数字字符替换为number。 例如,对于输入字符串 "a1b2c3",函数应该将其转换为 "anumberbnumbercnumber"。
输入:输入一个字符串 s,s 仅包含小写字母和数字字符。
输出:打印一个新的字符串,其中每个数字字符都被替换为了number
示例
- 输入:a1b2c3
- 输出:anumberbnumbercnumber
2.题解思路
👻方法1:替换法(辅助工具)
- 思路分析:遍历每个字符,判断是否为数字,满足数字在调用String的replace方法进行替换
// 将目标字符串的数字字符替换成`number`
public String convert(String target){
// 遍历字符串数据,判断是否为数字字符,是则进行替换
for(char ch : target.toCharArray()){
if(Character.isDigit(ch)){
target = target.replace(ch + "","number");
}
}
// 返回替换后的字符串
return target;
}
复杂度分析
时间复杂度:O(n)n 为字符串长度
空间复杂度:O(m)此处空间占用取决于替换后的字符串长度(调用java方法实现替换)
👻方法2:辅助数组(统计数字个数,填充扩容后的新数组)
- 思路分析:统计数字个数,从后往前填充数组(不要局限于方法能够一步到位,拆分步骤实现思路更加清晰)
- 统计数字个数:由于要确定扩容数组的大小,因此此处要统计源字符串的数字个数,避免未知的频繁扩容操作
- 填充扩容后的新数组:
public String convert(String target){
// 遍历字符串数据,判断是否为数字字符,进行统计
int count = 0;
char[] targetArr = target.toCharArray();
for(char ch : targetArr){
if(Character.isDigit(ch)){
count++;
}
}
// 确定扩容数组的大小
char[] convertArr = new char[target.length() + 5 * count]; // number 6个字符,减去原有提供的1个字符
// 遍历源字符串
int cur = 0; // cur指向新扩容数字的填充位置
for(char ch:targetArr){
// 如果是字符直接填充
if(Character.isLetter(ch)){
convertArr[cur++] = ch; // 填充字母,指针后移
}
// 如果是数字,进行替换
if(Character.isDigit(ch)){
convertArr[cur++] = 'n';
convertArr[cur++] = 'u';
convertArr[cur++] = 'm';
convertArr[cur++] = 'b';
convertArr[cur++] = 'e';
convertArr[cur++] = 'r';
}
}
// 返回替换后的字符串
return new String(convertArr);
}
复杂度分析
时间复杂度:O(n)n 为字符串长度
空间复杂度:O(m)此处空间占用取决于替换后的字符串长度(调用java方法实现替换)
扩展说明:如果题目要求只能在原数组基础上扩容,那么考虑从后往前进行遍历填充,避免其他元素的整体移动的复杂性
- 计算数字个数,随后对数组进行扩容(
Arrays.copyOf(targetArr, target.length() + 5 * count)) - 逆序遍历扩容数组,通过两个指针来处理新数组元素:一个是
cur(指向当前填充位置)、一个是i(指向当前遍历位置),从后往前进行遍历cur从后往前,其起点为convertArr.length - 1i从后往前,其起点为targetArr.length - 1(从target的有效位置开始逆序遍历)
- ==从后往前:==此处选择从后往前遍历的做法考虑主要是为了避免从前往后覆盖元素还要考虑整体数组元素的移动问题,从后往前遍历新数组打足了提前量,不会出现覆盖问题
// 统计数字个数+在现有数组基础上扩容
public String convert(String target) {
// 遍历字符串数据,判断是否为数字字符,进行统计
int count = 0;
char[] targetArr = target.toCharArray();
for (char ch : targetArr) {
if (Character.isDigit(ch)) {
count++;
}
}
// 确定扩容数组的大小
char[] convertArr = Arrays.copyOf(targetArr, target.length() + 5 * count); // number 6个字符,减去原有提供的1个字符
// 遍历扩容数组,从后往前填充
int cur = convertArr.length - 1; // cur指向新扩容数字的填充位置(从后往前)
for (int i = targetArr.length - 1; i >= 0; i--) { // i 指向遍历元素(如果出现替换则i也要保持同步前进)
if (Character.isLetter(convertArr[i])) {
convertArr[cur--] = convertArr[i]; // 非数字直接填充
}
if (Character.isDigit(convertArr[i])) {
// 数字,逆序填充(rebmun)
convertArr[cur--] = 'r';
convertArr[cur--] = 'e';
convertArr[cur--] = 'b';
convertArr[cur--] = 'm';
convertArr[cur--] = 'u';
convertArr[cur--] = 'n'; // 填充完成,i继续遍历下个元素
}
}
// 返回替换后的字符串
return new String(convertArr);
}
🟡151-反转字符串中的单词
1.题目内容
给你一个字符串 s ,请你反转字符串中 单词 的顺序。
单词 是由非空格字符组成的字符串。s 中使用至少一个空格将字符串中的 单词 分隔开。
返回 单词 顺序颠倒且 单词 之间用单个空格连接的结果字符串。
**注意:**输入字符串 s中可能会存在前导空格、尾随空格或者单词间的多个空格。返回的结果字符串中,单词间应当仅用单个空格分隔,且不包含任何额外的空格。
示例 1:
输入:s = "the sky is blue"
输出:"blue is sky the"
示例 2:
输入:s = " hello world "
输出:"world hello"
解释:反转后的字符串中不能存在前导空格和尾随空格。
示例 3:
输入:s = "a good example"
输出:"example good a"
解释:如果两个单词间有多余的空格,反转后的字符串需要将单词间的空格减少到仅有一个。
2.题解思路
👻方法1:去首尾空格、切割、逆序遍历、拼接
- 思路分析:中规中矩处理字符串
- (1)去首尾空格:
trim - (2)切割:
split(借助正则表达式进行切割\\s+,因为存在一个或多个空格字符串拼接的情况) - (3)逆序遍历:逆序遍历切割后的数组
- (4)拼接:将逆序的顺序进行拼接(以单个空格间隔),返回相应结果
- (1)去首尾空格:
// 字符串切割、逆序遍历并拼接输出
public String reverseWords(String s) {
// 对字符串进行首尾去除空格处理
s = s.trim();
// 切割字符串(一个或多个空格)
String[] strs = s.split("\\s+"); // 通过正则表达式切割
// 逆序遍历字符串,拼接输出
StringBuffer res = new StringBuffer();
for(int i=strs.length-1;i>=0;i--){
res.append(strs[i]);
// 判断是否要添加空格(如果是最后一个元素则不需要加空格)
if(i!=0){
res.append(" ");
}
}
// 返回结果
return res.toString();
}
复杂度分析
时间复杂度:O(n)n 为输入字符串的长度
空间复杂度:O(n)存储字符串分割之后的结果
纯工具类方法
// 字符串切割、反转数组、拼接
public String reverseWords(String s) {
// 1.对字符串进行首尾去除空格处理
s = s.trim();
// 2.切割字符串(一个或多个空格)
String[] strs = s.split("\\s+"); // 通过正则表达式切割
// 3.借助工具类进行逆序处理
List<String> list = Arrays.asList(strs);
Collections.reverse(list);
// 4.借助工具类拼接
return String.join(" ",list);
}
👻方法2:栈
- 思路分析:自定义切割方法,用栈存储单词,然后依次弹出栈拼接新数据
- 切割方法核心:
- 先将源字符串去除首尾空格,然后遍历字符串
- 定义一个临时的字符串缓冲区
word存储目前遍历的单词,如果遍历的是字符则拼接,如果遇到空格说明当前单词遍历结束了,需要将word入栈并清空缓冲区进行下一个单词的临时存储 - 遍历结束后需记得将最后一个缓冲区的内容入栈
- 遍历栈元素,然后依次拼接
- 切割方法核心:
/**
* 151 反转字符串中的单词
*/
public class Solution3 {
// 栈:存储单词,遍历拼接
public String reverseWords(String s) {
// 1.对字符串进行首尾去除空格处理
s = s.trim();
// 2.自定义分割方法遍历字符串入栈
Stack<String> stack = new Stack<>();
// 找到单词的起点和终点入栈
StringBuffer word = new StringBuffer();
for (int i = 0; i < s.length(); i++) {
char cur = s.charAt(i);
if (Character.isLetter(cur) || Character.isDigit(cur)) {
// 遇到字符则拼接
word.append(cur);
} else if (cur == ' ') {
// 遇到空格说明遍历到当前单词的尾部,构成一个完整的单词(且非空),需入栈并重置临时处理区
if (!"".equals(word.toString())) {
stack.push(word.toString()); // 入栈
word = new StringBuffer(); // 重置
}
}
}
// 将最后一个缓冲区数据入栈
stack.push(word.toString());
// 3.依次弹出栈元素
StringBuffer res = new StringBuffer();
int cnt = 0;
int size = stack.size();
while (!stack.isEmpty()) {
res.append(stack.pop());
cnt++;
if (cnt != size) {
res.append(" ");
}
}
// 返回结果
return res.toString();
}
}
👻方法2:双指针(去除首尾空格、切割字符串、原地反转数组、拼接)
- 思路分析:核心去除首尾空格、切割字符串、原地反转数组(双指针反转)、拼接
/**
* 151 反转字符串中的单词
*/
public class Solution151 {
public String reverseWords(String s) {
// 1.取出元素首尾空格
s = s.trim();
// 2.切割字符串
String[] strs = s.split("\\s+");
// 3.交换字符串数组元素
int left = 0,right = strs.length-1;
while(left<right){
// 交换元素
String temp = strs[left];
strs[left] = strs[right];
strs[right] = temp;
// 指针靠拢
left++;
right--;
}
// 4.将数组拼接
return String.join(" ", strs);
}
}
复杂度分析
时间复杂度:O(n) n 为字符串长度,需遍历字符串
空间复杂度:O(n)额外的空间辅助需依赖于切割字符串之后存储的单词
⚽KMW055-右旋转字符串
1.题目内容
字符串的右旋转操作是把字符串尾部的若干个字符转移到字符串的前面。给定一个字符串 s 和一个正整数 k,请编写一个函数,将字符串中的后面 k 个字符移到字符串的前面,实现字符串的右旋转操作。
例如,对于输入字符串 "abcdefg" 和整数 2,函数应该将其转换为 "fgabcde"。
输入:输入共包含两行,第一行为一个正整数 k,代表右旋转的位数。第二行为字符串 s,代表需要旋转的字符串。
输出:输出共一行,为进行了右旋转操作后的字符串。
样例输入:
2
abcdefg
样例输出:
fgabcde
数据范围:1 <= k < 10000, 1 <= s.length < 10000
2.题解思路
👻方法1:遍历+拼接
- 思路分析:从题意分析,右旋体现的效果就是将后K位的字符串移动到头部,因此可以用字符串遍历+拼接的方式实现,先遍历后K位,然后遍历前n-k位,组合成新字符串
// 指定目标字符串和整数K,将后K位的数字移动到头部
public String rightRotate(String target, int k) {
// 定义结果字符串
StringBuffer res = new StringBuffer();
// 先拼接后K位
int len = target.length();
for (int i = len - k; i < len; i++) {
res.append(target.charAt(i));
}
// 再拼接前面的内容
for (int i = 0; i < len - k; i++) {
res.append(target.charAt(i));
}
// 返回结果
return res.toString();
}
复杂度分析
时间复杂度:O(n) n为字符串长度
空间复杂度:O(n) n为字符串长度
👻方法2:局部反转+整体反转
- 思路分析:上述的【方案1】中需要依赖于额外的空间,如果在不依赖于额外的空间基础上(需注意JAVA无法实现直接在字符串上交换元素,必须借助辅助数组,其他语言可能可以),可以考虑通过局部反转+整体反转的思路实现
- 以
abcdefg为例,k 取 2 则正常右旋结果应该为fgabcde。基于局部反转+整体反转的思路分析如下:(注意区分先局部后整体、先整体后局部的区间取值问题)- k=2将源字符串划分为两个区域
"abcde fg",因此可以将这两个字符串分别进行局部反转,然后再将反转后的字符串进行一个整体的反转,进而得到一个负负得正的效果- 将两个字符串进行局部反转:
edcba gf(区间划分[0,len-k-1]、[len-k,len-1]) - 进行整体反转:
fgabcde=>得到了正确的右旋结果,进而可以通过原地反转的方式实现右旋效果
- 将两个字符串进行局部反转:
- k=2将源字符串划分为两个区域
- 以
abcdefg为例,k 取 2 则正常右旋结果应该为fgabcde。如果采用的是先整体反转后局部反转,则注意区间取值- 先整体反转
gfedcba - 局部反转:此处局部反转的划分区间应该为(
[0,k-1]、[k,len-1])
- 先整体反转
- 以
// 思路2:局部反转+真题反转(空间复杂度:O(n))
public String rightRotate(String target, int k) {
char[] targetArr = target.toCharArray();
int len = target.length();
// 局部反转
reverseStr(targetArr, 0, len - k - 1);
reverseStr(targetArr, len - k, len - 1);
// 整体反转
reverseStr(targetArr, 0, len - 1);
// 返回反转后的字符串数据
return new String(targetArr);
}
// 自定义反转方法(原地反转数组元素):[start,end]闭区间
public void reverseStr(char[] targetArr, int start, int end) {
while (start < end) {
char temp = targetArr[start];
targetArr[start] = targetArr[end];
targetArr[end] = temp;
// 交换完成,指针靠拢
start++;
end--;
}
}
复杂度分析
时间复杂度:O(n)n 为字符串长度,需遍历整个字符串
空间复杂度:O(n)JAVA 无法直接原地交换字符串元素内容,因此需借助辅助数组来实现,空间复杂度还是O(n)
🟢028-实现strStr
1.题目内容
给你两个字符串 haystack 和 needle ,请你在 haystack 字符串中找出 needle 字符串的第一个匹配项的下标(下标从 0 开始)。如果 needle 不是 haystack 的一部分,则返回 -1 。
示例 1:
输入:haystack = "sadbutsad", needle = "sad"
输出:0
解释:"sad" 在下标 0 和 6 处匹配。
第一个匹配项的下标是 0 ,所以返回 0 。
示例 2:
输入:haystack = "leetcode", needle = "leeto"
输出:-1
解释:"leeto" 没有在 "leetcode" 中出现,所以返回 -1 。
2.题解思路
👻方法1:找起点+截取字符串进行匹配
- 思路分析:找到匹配的起点,然后截取指定区域的字符串和needle进行比较,如果匹配则直接返回索引起点(题中限定返回第一个匹配的索引起点位置)。如果不匹配则继续找下一个起点校验,需注意字符串截取的终点不能超出haystack字符串长度
- 枚举原串
ss中的每个字符作为「发起点」,每次从原串的「发起点」和匹配串的「首位」开始尝试匹配(可以通过截取字符串的形式进行匹配校验,也可以自定义匹配方法)- 匹配成功:返回本次匹配的原串「发起点」
- 匹配失败:枚举原串的下一个「发起点」,重新尝试匹配
- 枚举原串
public class Solution1 {
/**
* 返回needle在haystack中出现的第1个位置
*/
public int strStr(String haystack, String needle) {
// return haystack.indexOf(needle);
// 遍历字符串
int hLen = haystack.length();
char firstCh = needle.charAt(0);
int nLen = needle.length();
for (int i = 0; i < hLen; i++) {
// 如果首字符匹配则开始校验
if (haystack.charAt(i) == firstCh) {
// 截取字符串进行验证,如果有匹配的直接返回(返回第1个匹配的内容)
if (i + nLen <= hLen) {
if (haystack.substring(i, i + nLen).equals(needle)) {
return i;
}
}
}
}
// 没有匹配的内容
return -1;
}
}
复杂度分析
时间复杂度:O(n)需遍历字符串数组
空间复杂度:O(1)
硬核解法:用字符串原生的操作方法
public int strStr(String haystack, String needle) {
return haystack.indexOf(needle);
}
自定义匹配校验方法:非截取字符串方式(一一匹配指定范围的字符串)
// 返回needle在haystack中出现的第1个位置
public int strStr(String haystack, String needle) {
// return haystack.indexOf(needle);
// 遍历字符串
int hLen = haystack.length();
char firstCh = needle.charAt(0);
int nLen = needle.length();
for (int i = 0; i < hLen; i++) { // 可以在此处限定i<hLen-nLen 界定边界
// 如果首字符匹配则开始校验
if (haystack.charAt(i) == firstCh) {
// 自定义方法校验字符串是否匹配
int start = i, end = i + nLen; // haystack 校验的起始位置
int cur = 0; // needle 校验的位置
boolean valid = true;
if (end <= hLen) { // end 不能越界
for (int k = start; k < end; k++) {
if (haystack.charAt(k) != needle.charAt(cur++)) {
valid = false;
break; // 出现不匹配,无需继续校验
}
}
if (valid) {
return i; // 匹配方返回
}
}
}
}
// 没有匹配的内容
return -1;
}
寻找每一个可能的起点,确定校验范围进行校验
- ①
for:外层循环校验第一个字符是否匹配 - ② 当找到满足的位置
idx,确定[idx,end]范围,基于这个起点校验字符串是否匹配
/**
* 🟢 028 找出字符串第一个匹配项的下标
*/
public class Solution028 {
/**
* 在haystack找到第一个匹配needle的字符串的索引位置
*/
public int strStr(String haystack, String needle) {
int hLen = haystack.length(), nLen = needle.length();
int first = needle.charAt(0);
// 先找到每一个起点相同的位置,然后校验基于这个起点是否满足
for (int i = 0; i < hLen; i++) {
// 校验首字母是否匹配
if (haystack.charAt(i) == first) {
int end = Math.min(i + nLen, hLen); // 限定校验字符串(注意越界问题)
String subStr = haystack.substring(i, end);
if (subStr.equals(needle)) {
return i;
}
}
}
// 没有找到匹配的内容
return -1;
}
}
🟢459-重复的子字符串
1.题目内容
给定一个非空的字符串 s ,检查是否可以通过由它的一个子串重复多次构成。
示例 1:
输入: s = "abab"
输出: true
解释: 可由子串 "ab" 重复两次构成。
示例 2:
输入: s = "aba"
输出: false
示例 3:
输入: s = "abcabcabcabc"
输出: true
解释: 可由子串 "abc" 重复四次构成。 (或子串 "abcabc" 重复两次构成。)
2.题解思路
👻方法1:前缀+倍数+规律校验
- 思路分析:结合题意整理核心要点
- 假设存在这么一个子串subStr满足题意,则subStr需要满足两个条件
- s 的长度是 subStr 长度的倍数
- subStr 是 s 的 前缀(通过n个subStr拼接可以构成s)
- 对于任意的
i∈[n′,n),有 s[i]=s[i−n′]
- 假设存在这么一个子串subStr满足题意,则subStr需要满足两个条件
/**
* 459 重复的子字符串
*/
public class Solution2 {
/**
* 前缀+倍数+规律
* 重复子串的满足条件:
* 1.前缀
* 2.倍数(subStr的长度是s的长度的倍数)
* 3.对于任意的 i∈[n',n),有 s[i]=s[i−n']
*/
public boolean repeatedSubstringPattern(String s) {
int n = s.length();
// 限定i为子串的长度(从1-n/2)
for (int i = 1; i <= n / 2; i++) {
// 只是校验满足倍数关系的子串
if (n % i == 0) { // i 为当前设定的子串长度
// 校验是否满足i∈[n',n),有 s[i]=s[i−n']
boolean match = true;
for (int j = i; j < n; j++) {
if (s.charAt(j) != s.charAt(j - i)) {
match = false; // 一旦不匹配无需后续校验直接进行下一个长度的判断
break;
}
}
// 校验通过返回true
if (match) { // 找到匹配直接返回
return true;
}
}
}
// 其他情况无匹配
return false;
}
}
复杂度分析
时间复杂度:O(n2)枚举
i遍历s空间复杂度:O(1)
👻方法2:暴力法(❌超时)
- 思路分析:找到所有子串,判断子串是否可以通过重复拼接得到s;此处暴力超时主要是没有提前对子串进行过滤,而是默认将所有子串都校验一遍导致超时
- 假设存在这么一个子串subStr满足题意,则subStr需要满足两个条件
- s 的长度是 subStr 长度的倍数
- subStr 是 s 的前缀(通过n个subStr拼接可以构成s)、子串的长度不能超过
sLen/2
- 假设存在这么一个子串subStr满足题意,则subStr需要满足两个条件
/**
* 459 重复的子字符串
*/
public class Solution1 {
// todo 超时
// 暴力法:找到所有子串,判断其可否由子串重复拼接构成
public boolean repeatedSubstringPattern(String s) {
for (int i = 0; i < s.length(); i++) {
for (int j = i + 1; j < s.length(); j++) { // j 从i+1开始,确保起码子串非空
String subStr = s.substring(i, j);
// 判断子串是否拼接成s
if (valid(subStr, s)) {
return true; // 存在满足条件的子串直接返回true
}
}
}
// 不存在
return false;
}
public boolean valid(String subStr, String s) {
/**
* 获取subStr大小,如果subStr可重复拼接成s应该满足两个条件
* 1.sLen % subStrLen == 0
* 2.经过多次拼接后生成的字符串和s完全一致
*/
int sLen = s.length();
int subStrLen = subStr.length();
// 空字符串、子串大于sLen一半(无法通过重复得到s)
if (subStrLen == 0 || subStrLen > sLen / 2) {
return false;
}
if (sLen % subStrLen != 0) {
return false;
}
int turn = sLen / subStrLen;
StringBuffer str = new StringBuffer();
for (int i = 0; i < turn; i++) {
str.append(subStr);
}
return s.equals(str.toString());
}
}
复杂度分析
- 时间复杂度:O(n2)暴力遍历校验所有可能的子串
- 空间复杂度:O(n)需要一些辅助的字符串空间占用
👻方法3:规律法
- 思路分析:判断字符串s是否由重复子串组成,只要两个s拼接在一起,里面还出现一个s的话(也就是说要找一个中间的
s既不能是第1个位置,也不能是中间位置),就说明是由重复子串组成- 即拼接两个s,找到s的idx位置,这个idx不能是0(从s+s的下标为1的索引位置开始遍历),也不能是s.length(判断idx不能在拼接位置)
public boolean repeatedSubstringPattern(String s) {
return (s+s).indexOf(s,1) != s.length();
}
// strA.indexOf(needle,1)是判断字符串needle在strA中存在(从strA的下标为1的索引位置开始判断),且找到的这个索引位置不能为拼接的中点位置
🟢925-长按键入
1.题目内容
你的朋友正在使用键盘输入他的名字 name。偶尔,在键入字符 c 时,按键可能会被长按,而字符可能被输入 1 次或多次。
你将会检查键盘输入的字符 typed。如果它对应的可能是你的朋友的名字(其中一些字符可能被长按),那么就返回 True。
示例 1:
输入:name = "alex", typed = "aaleex"
输出:true
解释:'alex' 中的 'a' 和 'e' 被长按。
示例 2:
输入:name = "saeed", typed = "ssaaedd"
输出:false
解释:'e' 一定需要被键入两次,但在 typed 的输出中不是这样
2.题解思路
👻方法1:规律遍历法(双指针)
误区:此处需注意无法用set处理,因为name中可能会有重复字符出现,如果单纯考虑对typed进行去重操作,则会忽略掉重复元素的情况,不能覆盖所有用例
- 思路分析:定义双指针分别遍历两个字符串,然后根据题意处理指针:
nIdx用于遍历name、tIdx用于遍历typed(此处假设转化为字符数组处理n[]、t[])while(nIdx<nLen && tIdx<tLen)- 如果
n[nIdx]==t[tIdx]:两个指针继续向前移动,继续下一位校验 - 如果
n[nIdx]!=t[tIdx]:则分情况讨论- ①
tIdx==0:说明第1位就不相等,直接返回false - ②
tIdx!=0:说明可能typed键入了重复元素,需要跳过这些重复的元素,跳过操作完成再进行一次比较最新的tIdx位置字符与nIdx位置字符是否相等- 如果不相等则说明不匹配直接返回false
- 如果相等则两个指针继续向前移动,继续下一位校验
- ①
- 如果
- 上述遍历完成,需要校验剩余的字符串:通过比较各自索引位置和相应字符串大小即可知是否存在剩余
- ① 如果
name有剩余,说明typed无法匹配,直接返回false - ② 如果
typed有剩余,同理校验多出来的尾巴是否为重复元素导致,因此此处需要跳过重复元素,如果跳过更新之后满足tIdx==tLen说明匹配(多出来的是重复元素,typed可以顺利遍历完成)
- ① 如果
/**
* 🟢925 长按键入
*/
public class Solution2 {
// 双指针遍历思路
public boolean isLongPressedName(String name, String typed) {
int nLen = name.length(), tLen = typed.length();
// 分别定义指针用于遍历两个字符串
int nIdx = 0, tIdx = 0;
while (nIdx < nLen && tIdx < tLen) {
// 校验当前遍历元素是否匹配
char curN = name.charAt(nIdx);
char curT = typed.charAt(tIdx);
if (curN == curT) {
// 当前遍历元素匹配,两者继续向前移动
nIdx++;
tIdx++;
} else {
// 当前遍历元素不匹配则分情况讨论
// ① 如果第一个元素就不匹配则直接返回false
if (nIdx == 0) {
return false;
}
// ② 如果非第一个元素,则考虑是出现了重复键入的元素,typed需要跳过这些重复键入的元素
while (tIdx < tLen - 1 && typed.charAt(tIdx) == typed.charAt(tIdx - 1)) { // 注意数组越界处理
tIdx++;
}
// 当tIdx跨越了重复键入的元素之后,再次继续比较,如果此时还是不匹配则说明不满足
if (typed.charAt(tIdx) != curN) {
return false;
} else {
// 如果匹配,则两个指针继续向前移动
nIdx++;
tIdx++;
}
}
}
// 校验是否还有剩余元素没匹配完成
// ① 如果是name剩余,则说明typed字符无法完全匹配name
if (nIdx < nLen) {
return false;
}
// ② 如果是typed剩余,则校验是否是出现了多余的尾巴导致剩余(同理,跳过重复元素即可)
while (tIdx < tLen && typed.charAt(tIdx) == typed.charAt(tIdx - 1)) {
tIdx++;
}
// 判断tIdx可以顺利遍历到末尾,如果可以说明剩余的都是重复的尾巴
return tIdx == tLen;
}
}
复杂度分析
- 时间复杂度:O(m+n)需遍历两个字符串,m+n为两个字符串的长度
- 空间复杂度:O(1)定义指针辅助遍历,占用常数级空间
🟢844-比较含退格的字符串
1.题目内容
给定 s 和 t 两个字符串,当它们分别被输入到空白的文本编辑器后,如果两者相等,返回 true 。# 代表退格字符。
**注意:**如果对空文本输入退格字符,文本继续为空。
示例 1:
输入:s = "ab#c", t = "ad#c"
输出:true
解释:s 和 t 都会变成 "ac"。
示例 2:
输入:s = "ab##", t = "c#d#"
输出:true
解释:s 和 t 都会变成 ""。
示例 3:
输入:s = "a#c", t = "b"
输出:false
解释:s 会变成 "c",但 t 仍然是 "b"。
2.题解思路
👻方法1:模拟栈(处理 + 匹配)
- 思路分析:结合题意分析,最原始的方法就是分别处理
s和t的退格,将其转化为不含退格的字符串,然后再校验转化后的两个字符串是否匹配- 此处
StringBuffer相当于一个模拟栈,遇到退格则弹出最近加入的元素(即字符串末尾的元素),对于公共的逻辑处理部分可以抽离成公共方法进行调用
- 此处
/**
* 🟢844 比较含退格的字符串
*/
public class Solution1 {
// 处理 + 校验
public boolean backspaceCompare(String s, String t) {
// 分别处理两个字符串中的退格,将其转化为正确的字符串
StringBuffer sBuffer = new StringBuffer();
for (char cur : s.toCharArray()) {
if (cur != '#') {
sBuffer.append(cur);
} else {
// 遇到空格,需移除最近加入的元素
if(!sBuffer.isEmpty()){ // 有的删才执行
sBuffer.deleteCharAt(sBuffer.length() - 1);
}
}
}
// 同理处理t
StringBuffer tBuffer = new StringBuffer();
for (char cur : t.toCharArray()) {
if (cur != '#') {
tBuffer.append(cur);
} else {
// 遇到空格,需移除最近加入的元素
if(!tBuffer.isEmpty()){
tBuffer.deleteCharAt(tBuffer.length() - 1);
}
}
}
// 检验正常转化空格后的两个字符串是否一致
return sBuffer.toString().equals(tBuffer.toString()); // 需转化为字符串比较
}
}
复杂度分析
- 时间复杂度:O(m+n)需分别遍历两个字符串
- 空间复杂度:O(m+n)需构建辅助的
StringBuffer对象处理字符串
🟡008-字符串转换整数(atoi)
1.题目内容
请你来实现一个 myAtoi(string s) 函数,使其能将字符串转换成一个 32 位有符号整数。
函数 myAtoi(string s) 的算法如下:
- **空格:**读入字符串并丢弃无用的前导空格(
" ") - **符号:**检查下一个字符(假设还未到字符末尾)为
'-'还是'+'。如果两者都不存在,则假定结果为正。 - **转换:**通过跳过前置零来读取该整数,直到遇到非数字字符或到达字符串的结尾。如果没有读取数字,则结果为0。
- **舍入:**如果整数数超过 32 位有符号整数范围
[−231, 231 − 1],需要截断这个整数,使其保持在这个范围内。具体来说,小于−231的整数应该被舍入为−231,大于231 − 1的整数应该被舍入为231 − 1。
返回整数作为最终结果。
示例 1:
**输入:**s = "42"
**输出:**42
**解释:**加粗的字符串为已经读入的字符,插入符号是当前读取的字符。
带下划线线的字符是所读的内容,插入符号是当前读入位置。
第 1 步:"42"(当前没有读入字符,因为没有前导空格)
^
第 2 步:"42"(当前没有读入字符,因为这里不存在 '-' 或者 '+')
^
第 3 步:"42"(读入 "42")
^
示例 2:
**输入:**s = " -042"
输出:-42
解释:
第 1 步:" -042"(读入前导空格,但忽视掉)
^
第 2 步:" -042"(读入 '-' 字符,所以结果应该是负数)
^
第 3 步:" -042"(读入 "042",在结果中忽略前导零)
^
示例 3:
**输入:**s = "1337c0d3"
**输出:**1337
解释:
第 1 步:"1337c0d3"(当前没有读入字符,因为没有前导空格)
^
第 2 步:"1337c0d3"(当前没有读入字符,因为这里不存在 '-' 或者 '+')
^
第 3 步:"1337c0d3"(读入 "1337";由于下一个字符不是一个数字,所以读入停止)
^
示例 4:
**输入:**s = "0-1"
**输出:**0
解释:
第 1 步:"0-1" (当前没有读入字符,因为没有前导空格)
^
第 2 步:"0-1" (当前没有读入字符,因为这里不存在 '-' 或者 '+')
^
第 3 步:"0-1" (读入 "0";由于下一个字符不是一个数字,所以读入停止)
^
示例 5:
**输入:**s = "words and 987"
**输出:**0
解释:
读取在第一个非数字字符“w”处停止。
2.题解思路
👻方法1:if...else...
- 根据题意,主要分析4种字符的不同处理
- ① 首部空格:直接去除
- ② 符号位:三种情况("+"、"-"、"无符号"),新建一个变量用于保存符号位,返回前判断正负即可
- 此处注意针对符号位,如果存在符号位,则字符的校验从第2个位置开始;如果不存在符号位则字符的校验从第1个位置开始,需要注意区分
- ③ 非数字字符(注意此处不仅仅针对字母,还包括除数字之外的一些符号等字符):遇到首个非数字字符时,应立即返回
- ④ 数字字符:需要将数字字符转化为数字,然后进行数字拼接(针对拼接结果需要校验是否超出Integer阈值,如果超出则直接返回限定阈值)
- 数字字符转数字:
x = x - '0'(ascii码处理) - 数字拼接:
res = res * 10 + x - 阈值校验:针对阈值校验有两种思路
- 思路① 用
long定义并处理res,校验是否超出Integer.MAX/Integer.MIN,超出则返回限定阈值 - 思路② 用数位来处理,校验当前数位是否超出限定数位,超出则退出
- 思路① 用
- 数字字符转数字:
/**
* 🟡 008 字符串转整数(atoi) - https://leetcode.cn/problems/string-to-integer-atoi/
*/
public class Solution2 {
/**
* 四种字符的处理:
* ① 空格:去掉首部空格
* ② 符号:定义变量存储符号位(3种:正、负、无符号)
* ③ 非数字字符:直接返回
* ④ 数字字符:将数字字符转化为数字(ascii码转化),随后拼接数字
*/
public int myAtoi(String s) {
// ① 处理前后空格
s = s.trim(); // 借助String方法处理空格
if (s.equals("")) {
return 0; // 去重后的字符串为空则直接返回
}
// ② 校验符号
int sign = 1; // 定义符号位
int start = 0; // 字符校验的开始位置,需排除符号位的影响(如果存在符号位则字符判断从第2个位置开始,如果不存在则是从第1个位置开始)
long res = 0; // 定义整数结果,通过遍历更新
if (s.charAt(start) == '-') {
sign = -1;
start = 1; // 存在符号位,下一个遍历元素从第2个位置开始
} else if (s.charAt(start) == '+') {
sign = 1;
start = 1; // 存在符号位,下一个遍历元素从第2个位置开始
}
// 遍历元素
for (int i = start; i < s.length(); i++) {
// 校验字符是否为数字字符或者字母字符
char curCh = s.charAt(i);
if (!Character.isDigit(curCh)) {
break; // 遇到非数字字符(字母字符或者其他符号)直接退出
} else if (Character.isDigit(curCh)) {
// 将数字字符转化为数字并拼接
res = res * 10 + (curCh - '0');
// 校验值是否超出Integer值域,如果超出则直接返回(判断值域有两种,一种判断值大小,另一种则是判断数字位数是否超出Integer的限定)
if (res * sign > Integer.MAX_VALUE) return Integer.MAX_VALUE;
if (res * sign < Integer.MIN_VALUE) return Integer.MIN_VALUE;
}
}
return (int) res * sign;
}
}
复杂度分析
时间复杂度:O(N),其中 N 为字符串长度,线性遍历字符串占用 O(N) 时间
空间复杂度:O(N),删除首尾空格后需建立新字符串,最差情况下占用 O(N) 额外空间
优化思考:此处如果不使用String的
trim方法,可以自己处理首部空格,调整start初始值即可
public int myAtoi(String s) {
if (s == null || s.equals("")) {
return 0;
}
// ① 处理首部空格
int start = 0;
while (s.charAt(start) == ' ') {
start++;
if (start == s.length()) {
return 0; // 空格处理到达字符串尾部,则直接返回0
}
}
// ② 校验符号
int sign = 1; // 定义符号位
long res = 0; // 定义整数结果,通过遍历更新
if (s.charAt(start) == '-') {
sign = -1;
start++; // 存在符号位,下一个遍历元素从下个位置开始
} else if (s.charAt(start) == '+') {
sign = 1;
start++; // 存在符号位,下一个遍历元素从下个位置开始
}
// 遍历元素
for (int i = start; i < s.length(); i++) {
// 校验字符是否为数字字符或者字母字符
char curCh = s.charAt(i);
if (!Character.isDigit(curCh)) {
break; // 遇到非数字字符(字母字符或者其他符号)直接退出
} else if (Character.isDigit(curCh)) {
// 将数字字符转化为数字并拼接
res = res * 10 + (curCh - '0');
// 校验值是否超出Integer值域,如果超出则直接返回(判断值域有两种,一种判断值大小,另一种则是判断数字位数是否超出Integer的限定)
if (res * sign > Integer.MAX_VALUE) return Integer.MAX_VALUE;
if (res * sign < Integer.MIN_VALUE) return Integer.MIN_VALUE;
}
}
return (int) res * sign;
}
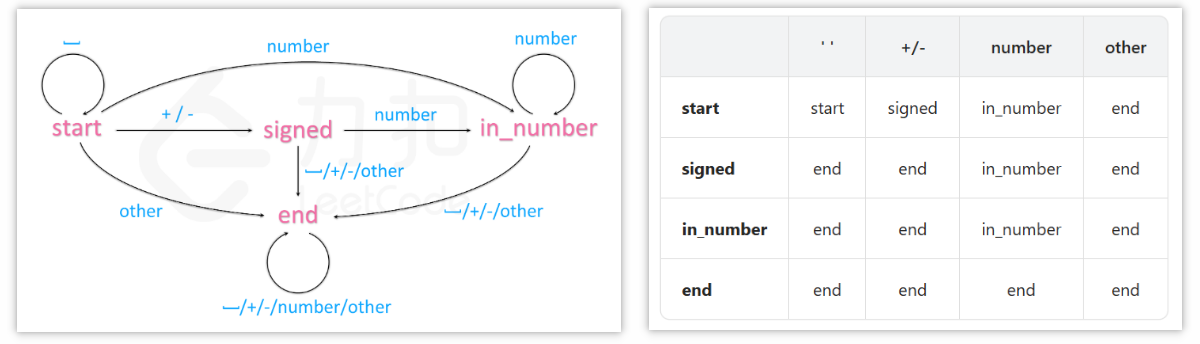
👻方法2:状态机
- 思路分析
class Solution {
public int myAtoi(String str) {
Automaton automaton = new Automaton();
int length = str.length();
for (int i = 0; i < length; ++i) {
automaton.get(str.charAt(i));
}
return (int) (automaton.sign * automaton.ans);
}
}
class Automaton {
public int sign = 1;
public long ans = 0;
private String state = "start";
private Map<String, String[]> table = new HashMap<String, String[]>() {{
put("start", new String[]{"start", "signed", "in_number", "end"});
put("signed", new String[]{"end", "end", "in_number", "end"});
put("in_number", new String[]{"end", "end", "in_number", "end"});
put("end", new String[]{"end", "end", "end", "end"});
}};
public void get(char c) {
state = table.get(state)[get_col(c)];
if ("in_number".equals(state)) {
ans = ans * 10 + c - '0';
ans = sign == 1 ? Math.min(ans, (long) Integer.MAX_VALUE) : Math.min(ans, -(long) Integer.MIN_VALUE);
} else if ("signed".equals(state)) {
sign = c == '+' ? 1 : -1;
}
}
private int get_col(char c) {
if (c == ' ') {
return 0;
}
if (c == '+' || c == '-') {
return 1;
}
if (Character.isDigit(c)) {
return 2;
}
return 3;
}
}
复杂度分析
时间复杂度:
空间复杂度:
🟡043-字符串相乘
1.题目内容
给定两个以字符串形式表示的非负整数 num1 和 num2,返回 num1 和 num2 的乘积,它们的乘积也表示为字符串形式。
**注意:**不能使用任何内置的 BigInteger 库或直接将输入转换为整数。
示例 1:
输入: num1 = "2", num2 = "3"
输出: "6"
示例 2:
输入: num1 = "123", num2 = "456"
输出: "56088"
2.题解思路
👻方法1:普通竖式
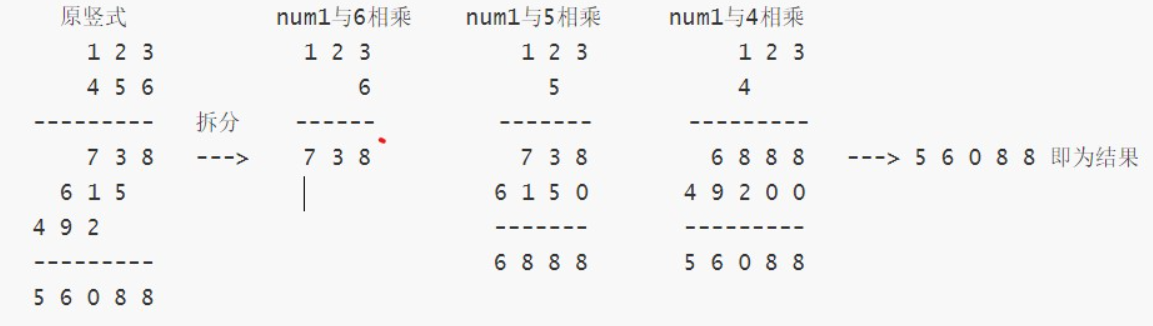
- 思路分析:基于竖式算法的思想,以
nums1 * nums2为例,其本质上就是将nums2中的每一位与nums1进行相乘,然后将相乘的结果进行累加(这个过程中需要注意0的数位填充问题)num2除了第一位的其他位与num1运算的结果需要 补 0- 计算字符串数字累加其实就是字符串相加的处理过程
- 注意点:此处需要注意,每个数位的处理都是从个位开始的,因此在处理结果的时候要注意逆序的问题,如果载入结果没有选用头插的话,对于结果而言要整体反转一遍才能得到正确的答案
/**
* 🟡 两个字符串相乘 - https://leetcode.cn/problems/multiply-strings/
*/
public class Solution1 {
/**
* 思路:竖式运算(num1作为基,遍历num2的每个数字与num1进行相乘并累加结果)
* 这个过程中注意数字0的填充以及字符串相加处理
*/
public String multiply(String num1, String num2) {
String res = "";
int n1 = num1.length(), n2 = num2.length();
// 如果num1、num2中有一个为0,则乘积返回0
if (num1.equals("0") || num2.equals("0")) {
return "0";
}
// 遍历nums2的每个字符进行相乘(逆序遍历处理,并在结果尾部补足0)
for (int i = n2 - 1; i >= 0; i--) {
// 处理当前相乘结果
StringBuffer temp = new StringBuffer();
// 对尾部补0
for (int j = 0; j < n2 - i - 1; j++) {
temp.append(0);
}
int curN2 = num2.charAt(i) - '0'; // 将当前遍历数字字符转为数字
// nums2的第i位与num1相乘
int carry = 0;
for (int j = n1 - 1; j >= 0 || carry != 0; j--) {
int x = (j >= 0) ? num1.charAt(j) - '0' : 0;
int product = curN2 * x + carry;
temp.append(product % 10);
carry = product / 10;
}
// 累加结果(将当前结果与新计算的结果进行求和作为新结果:两个字符串相加)
res = add(res, temp.reverse().toString()); // temp是正序补充元素,因此此处是返回逆序的字符串
}
// 返回结果
return res;
}
/**
* 两个字符串相加:需逆序相加处理
*/
public String add(String num1, String num2) {
int n1 = num1.length(), n2 = num2.length();
StringBuffer res = new StringBuffer();
int carry = 0;
for (int i = n1 - 1, j = n2 - 1; i >= 0 || j >= 0 || carry != 0; i--, j--) {
int val1 = (i >= 0 ? Integer.valueOf(num1.charAt(i) - '0') : 0);
int val2 = (j >= 0 ? Integer.valueOf(num2.charAt(j) - '0') : 0);
int sum = val1 + val2 + carry;
res.append(sum % 10);
carry = sum / 10;
}
// 返回结果
return res.reverse().toString(); // 逆序处理(或者在添加结果的时候采用头插,此处就不用整体reverse)
}
}
复杂度分析
时间复杂度:
空间复杂度:
🟢LCR 122-路径加密
1.题目内容
假定一段路径记作字符串 path,其中以 "." 作为分隔符。现需将路径加密,加密方法为将 path 中的分隔符替换为空格 "",请返回加密后的字符串。
示例 1:
输入:path = "a.aef.qerf.bb"
输出:"a aef qerf bb"
限制:
0 <= path.length <= 10000
2.题解思路
👻方法1:借助工具类
/**
* 🟢 LCR122 路径加密 - https://leetcode.cn/problems/ti-huan-kong-ge-lcof/description/
*/
public class Solution122_01 {
/**
* 将字符串path中的.分隔符替换成空格" ",随后返回加密后的字符串
*/
public String pathEncryption(String path) {
// 方式1:replace API 替换
// String res = path.replace(".", " ");
// return res;
// 方式2:字符串分隔 + 组合
String[] strs = path.split("\\.");
// String res = String.join(" ", strs);
StringBuffer sb = new StringBuffer();
for (int i = 0; i < strs.length; i++) {
if (!"".equals(strs[i])) {
sb.append(strs[i]);
if (i != strs.length - 1) {
sb.append(" "); // 添加间隔符
}
}
}
return sb.toString();
}
public static void main(String[] args) {
Solution122_01 solution = new Solution122_01();
solution.pathEncryption("......");
}
}
复杂度分析
时间复杂度:
空间复杂度:
123-xxx
1.题目内容
2.题解思路
👻方法1:
复杂度分析
时间复杂度:
空间复杂度:
