skill-02-链表
难度说明:🟢简单🟡中等🔴困难
学习资料
学习目标
- 掌握数据结构核心基础
- 借助数据结构完成常见题型
skill-02-链表
理论基础
1.核心理论
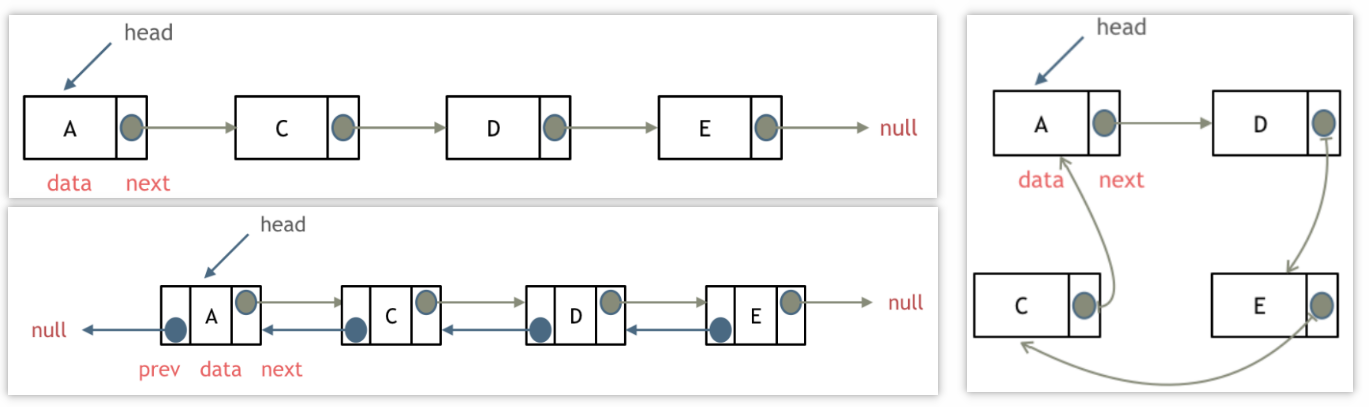
链表是一种通过指针串联在一起的线性结构,每一个节点由两部分组成,一个是数据域一个是指针域(存放指向下一个节点的指针),最后一个节点的指针域指向null(空指针的意思)
链表分类
- 单向链表、双向链表、循环链表
链表的存储方式
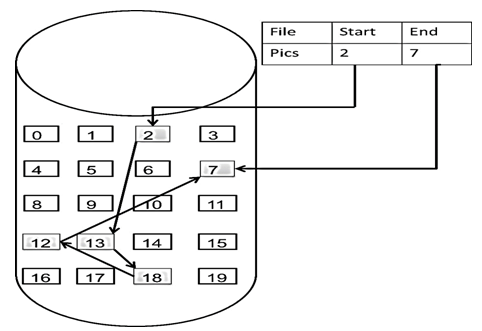
链表在内存中不是连续分布的,而是通过指针域的指针链接在内存的各个节点。即链表中的节点在内存中不是连续分布的 ,而是散乱分布在内存中的某地址上,分配机制取决于操作系统的内存管理
链表基础结构
/**
* 链表节点定义
*/
public class ListNode {
int val ; // 链表节点值
ListNode next; // 链表next节点指针
// 构造器
ListNode(){}
ListNode(int val){
this.val = val;
this.next = null;
}
// 头插概念(如果传入的next是一个链表,则当前节点会插入到这个next指向链表前)
ListNode(int val,ListNode next){
this.val = val;
this.next = next;
}
}
2.技巧总结
🚀链表基础操作
(1)添加节点
找到要插入的位置,然后将新节点插入,此处操作涉及到3个节点:分别是C(cur)、F(newNode)、D(cur.next)
- 时间复杂度:O(1),新增操作只对部分节点有影响,而不会影响到其他节点
// 插入新节点(将原有节点链接断开,然后构建新链接,需注意这个过程中保存数据)
ListNode cur = head;
while(cur!=null){
// 假设将F插入到C后面
if(cur.val=='C'){
// 执行插入操作
ListNode newNode = new ListNode('F'); // 创建新节点
ListNode nextNode = cur.next; // 记录当前cur的下一个节点
cur.next = newNode; // 插入新节点(断开C->D,构建C->F)
newNode.next = nextNode; // 构建F->D
}
// 指针后移
cur = cur.next;
}

(2)删除节点
对于单链表而言,删除节点则需要找到待删除节点的前一个节点prev,然后将这个节点的next指针指向原prev.next.next,基于此原prev.next就被挪出来的,如果是Java则由GC机制进行回收,不需要额外手动管理内存
- 时间复杂度:
- 节点删除操作的时间复杂度是O(1),删除操作只对部分节点有影响,而不会影响到其他节点
- 但是需注意对于单链表节点的删除,删除节点需要先查找到
prev然后执行删除操作,因此删除第N个节点的时间复杂度是O(N)
// 删除链表的第N个节点
ListNode cur = head;
// 遍历N-1个节点,找到第N-1个节点(待删除节点的前一个节点)
for(int i=1;i<N-1;i++){
cur = cur.next;
}
// 删除节点:prev.next = prev.next.next;
cur.next = cur.next.next;

(3)查找节点
// 查找节点
ListNode cur = head;
while(cur!=null){
if(cur.val=='XXX'){
return cur;
}
// 指针后移
cur=cur.next;
}
🚀链表 VS 数组
| 对比 | 新增/删除 | 查找 | 适用场景 |
|---|---|---|---|
| 链表 | O(1) | O(n) | 适用于数量不固定、增删频繁、查询较少的场景 |
| 数组 | O(n) | O(1) | 适用于数量固定、增删较少、查询频繁的场景 |
🚀链表常见题型分析
算法核心:针对链表问题,最重要的是画图理解,画出相应图示理解算法设计的细节,调试过程中通过打断点进行辅助
- 链表设计相关
- 单向链表、双向链表、相应链表节点的设计
- 链表操作相关(反转、交换)
- 206-反转链表:倒序概念,可以借助栈或者双指针滚动处理
- 024-两两交换链表中的节点:引入
dummy虚拟头节点构建新链表,然后两两交换(画图分析,明确两两交换涉及到的节点操作和节点顺序)
- 链表删除相关
- 思路:
- ① 对于链表元素删除的题型,为了避免对头尾的NPE判断,一般建议引入一个
dummy虚拟头节点构建新链表,然后对这个链表进行删除操作可以有效避免很多繁杂校验- dummy node 虚拟头节点(哨兵节点)的应用场景:作为新链表的头部;解决链表头部引起的极端问题
- 对于删除操作什么时候需要用到
dummy node?=》一般来说需要删除头节点的时候则需要借助dummy node辅助删除(因为对于单链表来说,删除节点操作需要借助前一个节点执行pre.next = pre.next.next操作)
- 对于删除操作什么时候需要用到
- dummy node 虚拟头节点(哨兵节点)的应用场景:作为新链表的头部;解决链表头部引起的极端问题
- ② 对于删除操作,链表的节点删除核心是找到待删除节点的前置节点
prev然后执行prev.next=prev.next.next
- ① 对于链表元素删除的题型,为了避免对头尾的NPE判断,一般建议引入一个
- 参考题型
- 203-移除链表元素
- 019-删除链表的倒数第N个节点
- 思路:
- 环形链表(I、II)
- 这两个题目的目的是:判断是否存在环、判断环的入口
- 哈希表
Set<ListNode>(重复判断):遍历+重复出现校验(如果遍历元素重复出现则说明存在环,当前遍历元素即为环的入口) - 快慢指针:龟兔赛跑概念
- 核心:快慢指针同时出发,快指针走两步、慢指针走一步,如果不存在环则快指针会先走到终点(链表尾部),如果存在环则必然会在某一时刻快慢指针相遇
- 如要寻找环的入口则判断是否存在环,如果存在则在相遇的那个点跳出,重新定义指针
cur从head起点 与 当前的slow同步出发,再次相遇则为环的入口
- 哈希表
- 这两个题目的目的是:判断是否存在环、判断环的入口
常见题型
🟢203-移除链表元素(同LCR 136-删除链表的节点)
1.题目内容
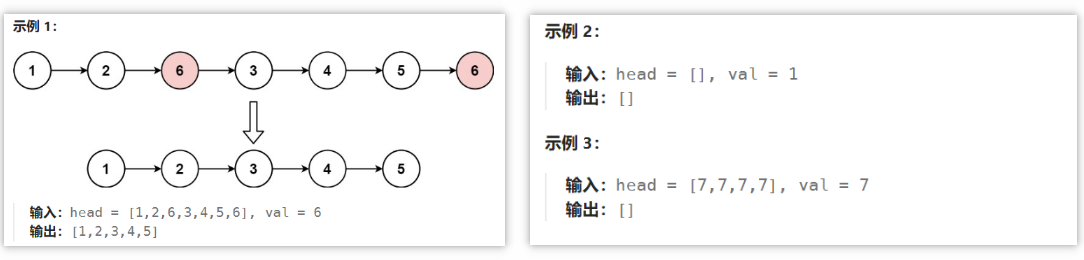
给你一个链表的头节点 head 和一个整数 val ,请你删除链表中所有满足 Node.val == val 的节点,并返回 新的头节点
2.题解思路
👻方法1:构建新链表(遍历老链表+将非val节点加入新链表)
/**
* 203 移除链表元素
*/
public class Solution1 {
/**
* 构建新链表:遍历原链表,将【非val的节点】加入新链表
*/
public ListNode removeElements(ListNode head, int val) {
// 定义虚拟头节点
ListNode dummy = new ListNode(-1);
ListNode cur = dummy; // 构建指针指向dummy
// 遍历链表head
ListNode pointer = head;
while(pointer!=null){
if(pointer.val != val){
// 如果值不为val则放入新链表
cur.next = new ListNode(pointer.val);
cur = cur.next; // 指针后移
}
pointer = pointer.next; // 指针后移
}
// 返回构建好的链表
return dummy.next;
}
}
复杂度分析
时间复杂度:O(n)n 为链表节点个数(需要遍历整个链表)
空间复杂度:O(n)构建新链表,最坏的情况下是一个待删除节点都没有
👻方法2:迭代(原地遍历删除)
- 思路分析:传统迭代方式,如果单纯删除的话,基于这种方式【第一个节点】无法删除,因此要引入一个虚拟头节点来进行辅助
/**
* 203 移除链表元素
*/
public class Solution2 {
/**
* 遍历删除(原地操作)
*/
public ListNode removeElements(ListNode head, int val) {
// 定义遍历指针
ListNode cur = head;
while (cur != null && cur.next != null) {
if (cur.next.val == val) {
cur.next = cur.next.next; // 删除节点
}else{
// 指针后移
cur = cur.next;
}
}
// 返回链表
return head;
}
}
/**
* 203 移除链表元素
*/
public class Solution2 {
/**
* 遍历删除(原地操作)
*/
public ListNode removeElements(ListNode head, int val) {
// 构建虚拟头节点
ListNode dummy = new ListNode(-1);
dummy.next = head; // 给head补充一个虚拟头节点
ListNode cur = dummy; // 定义遍历指针
while (cur.next != null) {
if (cur.next.val == val) {
cur.next = cur.next.next; // 删除节点
} else {
// 指针后移
cur = cur.next;
}
}
// 返回链表
return dummy.next;
}
}
复杂度分析
时间复杂度:O(n)n 为链表节点个数(需要遍历整个链表)
空间复杂度:O(1)
👻方法3:递归
- 思路分析:链表的定义具有递归的性质,因此链表题目常可以用递归的方法求解。这道题要求删除链表中所有节点值等于特定值的节点,可以用递归实现
class Solution {
public ListNode removeElements(ListNode head, int val) {
if (head == null) {
return head;
}
head.next = removeElements(head.next, val);
return head.val == val ? head.next : head;
}
}
复杂度分析
时间复杂度:O(n)n 为链表节点个数(需要遍历整个链表)
空间复杂度:O(n)空间复杂度主要取决于递归调用栈,最多不会超过 n 层
🟡707-设计链表
1.题目内容
你可以选择使用单链表或者双链表,设计并实现自己的链表。
单链表中的节点应该具备两个属性:val 和 next 。val 是当前节点的值,next 是指向下一个节点的指针/引用。
如果是双向链表,则还需要属性 prev 以指示链表中的上一个节点。假设链表中的所有节点下标从 0 开始。
实现 MyLinkedList 类:
MyLinkedList()初始化MyLinkedList对象。int get(int index)获取链表中下标为index的节点的值。如果下标无效,则返回-1。void addAtHead(int val)将一个值为val的节点插入到链表中第一个元素之前。在插入完成后,新节点会成为链表的第一个节点。void addAtTail(int val)将一个值为val的节点追加到链表中作为链表的最后一个元素。void addAtIndex(int index, int val)将一个值为val的节点插入到链表中下标为index的节点之前。如果index等于链表的长度,那么该节点会被追加到链表的末尾。如果index比长度更大,该节点将 不会插入 到链表中。void deleteAtIndex(int index)如果下标有效,则删除链表中下标为index的节点。
示例:
输入
["MyLinkedList", "addAtHead", "addAtTail", "addAtIndex", "get", "deleteAtIndex", "get"]
[[], [1], [3], [1, 2], [1], [1], [1]]
输出
[null, null, null, null, 2, null, 3]
解释
MyLinkedList myLinkedList = new MyLinkedList();
myLinkedList.addAtHead(1);
myLinkedList.addAtTail(3);
myLinkedList.addAtIndex(1, 2); // 链表变为 1->2->3
myLinkedList.get(1); // 返回 2
myLinkedList.deleteAtIndex(1); // 现在,链表变为 1->3
myLinkedList.get(1); // 返回 3
2.题解思路
👻方法1:单链表设计
中规中矩按照单链表的思路(核心要点head、curSize),根据题目提示构建链表,先完善一个版本,避免过程中投机取巧,版本稳定再进行优化
- 思路分析:单链表节点设计(定义链表头节点head和curSize当前链表长度)
- 初始化链表:head 构建虚拟头节点(在处理链表的过程中需要排除head节点)
- curSize:定义当前链表元素个数(随着链表节点的插入、删除而变化),也用于快速校验索引是否有效
- index:索引的有效取值范围(
[0,curSize)) 在边界判断的时候需要注意 index 的取值
class MyLinkedList {
// 定义链表头节点
ListNode head;
// 有效的index集合([0,curSize))
int curSize; // 维护当前链表长度
// 初始化链表
public MyLinkedList() {
head = new ListNode(-1); // 构建虚拟头节点
}
// 获取链表中下标为index的节点的值(下标无效返回-1)
public int get(int index) {
if (index < 0 || index >= curSize) {
return -1;
}
// 遍历链表
ListNode cur = head;
for (int i = 0; i <= index; i++) {
cur = cur.next;
}
return cur.val;
}
// 添加一个节点到头部
public void addAtHead(int val) {
// 构建新节点
ListNode newNode = new ListNode(val);
// 将链表加入到头部
newNode.next = head.next;
head.next = newNode;
curSize++;
}
// 添加一个节点到尾部
public void addAtTail(int val) {
ListNode cur = head;
for (int i = 0; i < curSize; i++) {
cur = cur.next;
}
ListNode newNode = new ListNode(val);
newNode.next = null;
cur.next = newNode;
curSize++;
}
// 插入一个节点到指定index位置之前(如果index==链表长度则插入尾部,如果index>链表长度则不执行插入)
public void addAtIndex(int index, int val) {
if (index == curSize) {
addAtTail(val); // 添加到尾部
} else if (index > curSize) {
return;
} else {
ListNode cur = head;
for (int i = 0; i < index; i++) {
cur = cur.next;
}
// 插入节点到指定位置
ListNode newNode = new ListNode(val);
ListNode nextNode = cur.next; // 记录cur.next
cur.next = newNode;
newNode.next = nextNode;
curSize++;
}
}
// 如果链表有效则删除链表中指定index的节点
public void deleteAtIndex(int index) {
if (index < 0 || index >= curSize) {
return;
}
// 删除链表指定index位置的节点
ListNode cur = head;
for (int i = 0; i < index; i++) {
cur = cur.next;
}
// 删除节点
if (cur.next != null) {
cur.next = cur.next.next;
curSize--;
}
}
public static void main(String[] args) {
MyLinkedList obj = new MyLinkedList();
obj.addAtHead(1);
obj.printLink();
obj.addAtHead(3);
obj.printLink();
obj.addAtTail(3);
obj.printLink();
obj.addAtIndex(1, 2);
obj.printLink();
System.out.println(obj.get(1));
obj.deleteAtIndex(1);
obj.printLink();
System.out.println(obj.get(1));
}
public void printLink() {
List<Integer> list = new ArrayList<>();
ListNode cur = head;
while (cur != null) {
list.add(cur.val);
cur = cur.next;
}
System.out.println(list);
}
}
复杂度分析
时间复杂度:
初始化:O(1)
get:O(index)需遍历到索引位置
addAtHead:O(1)
addAtTail:O(curSize)需遍历到尾部
addAtIndex:O(index)需遍历到索引位置
空间复杂度:函数的单次调用的空间复杂度为O(1),总体的空间复杂度为O(n)
👻方法2:双向链表
复杂度分析
时间复杂度:
空间复杂度:
🟢206-反转链表
1.题目内容
给你单链表的头节点 head ,请你反转链表,并返回反转后的链表
2.题解思路
👻方法1:辅助栈(辅助集合反转)
思路分析:借助辅助集合进行反转,遍历一遍链表元素加入指定集合,然后基于链表元素的逆序构建新链表
队列:如果是正向遍历封装到队列类型的集合,则逆序遍历这个队列构建新链表
- Deque 理解Java中Deque双向队列的用法
- 栈特性:
push、pop - 队列特性:
offer、poll可以指定方向- offerFirst 表示队列头插入,那么如果是队列方式取出(先进先出)的话则需搭配
pollLast(从另一头取),如果是栈方式取出(先进后出)的话则需搭配pollLast(注意不要想当然概念理解这个方向,可以借助图和举例来理解,避免概念混淆) - 同理:
offerLast+pollFirst是队列用法;offerLast+pollLast是栈用法
- offerFirst 表示队列头插入,那么如果是队列方式取出(先进先出)的话则需搭配
- 栈特性:
/** * 206 反转链表 */ public class Solution2 { // 借助辅助集合(队列|栈)构建新链表 public ListNode reverseList(ListNode head) { // 借助集合辅助(队列) Deque<ListNode> queue = new LinkedList<>(); // 遍历链表 ListNode cur = head; while(cur!=null){ // queue.push(cur); queue.offerFirst(cur); // offerLast // 指针后移 cur = cur.next; } // 逆序遍历辅助队列(弹出元素,构建新链表) ListNode dummy = new ListNode(-1); // 定义虚拟头节点 ListNode pointer = dummy; // 定义指针指向dummy while(!queue.isEmpty()){ // pointer.next = queue.pop(); // 弹出元素,构建链表 pointer.next = queue.pollFirst(); // 弹出元素,构建链表 pollLast pointer = pointer.next; // 指针后移 } pointer.next = null; // 用于处理 Error - Found cycle in the ListNode // 返回构建的新链表 return dummy.next; } }- Deque 理解Java中Deque双向队列的用法
栈:先入后出的特性,正向遍历链表,然后依次弹出栈元素,基于弹出的元素构建新链表
/** * 206 反转链表 */ public class Solution1 { // 借助辅助集合(队列|栈)构建新链表 public ListNode reverseList(ListNode head) { // 借助栈辅助 Stack<ListNode> stack = new Stack<>(); // 遍历链表 ListNode cur = head; while(cur!=null){ stack.push(cur); // 指针后移 cur = cur.next; } // 遍历辅助栈(弹出元素,构建新链表) ListNode dummy = new ListNode(-1); // 定义虚拟头节点 ListNode pointer = dummy; // 定义指针指向dummy while(!stack.isEmpty()){ pointer.next = stack.pop(); // 弹出元素,构建链表 pointer = pointer.next; // 指针移动 } pointer.next = null; // 用于处理 Error - Found cycle in the ListNode // 返回构建的新链表 return dummy.next; } }
复杂度分析
时间复杂度:O(n)n 为链表节点个数
空间复杂度:O(n)需借助辅助集合(队列/栈)构建新链表
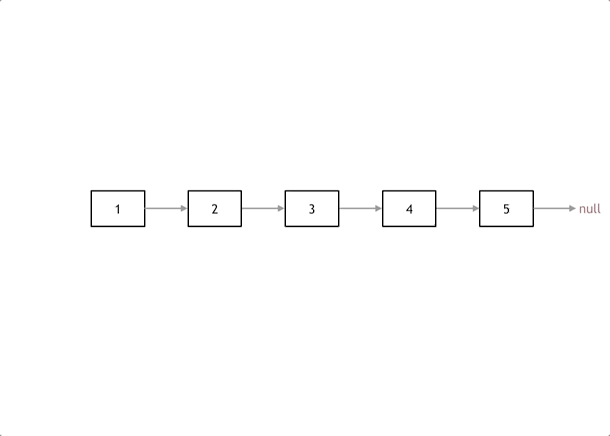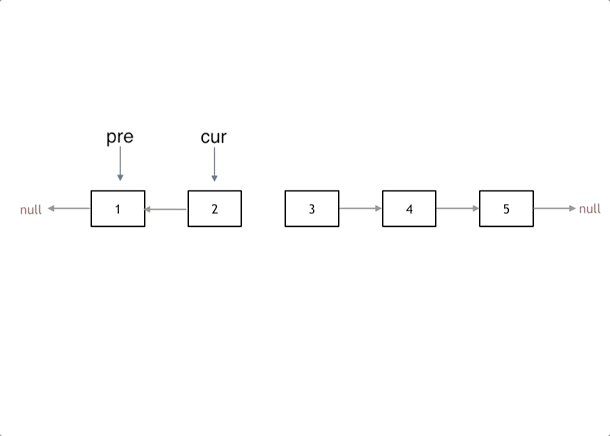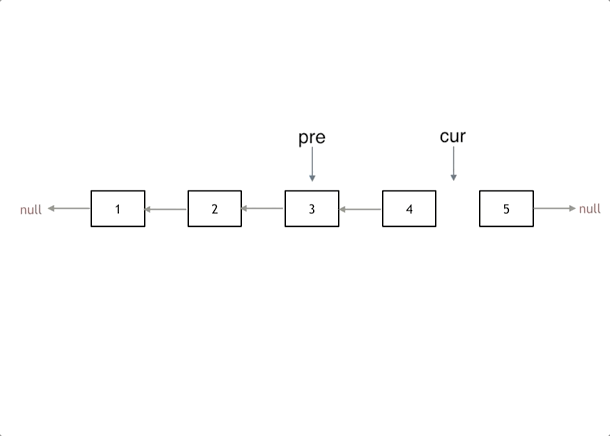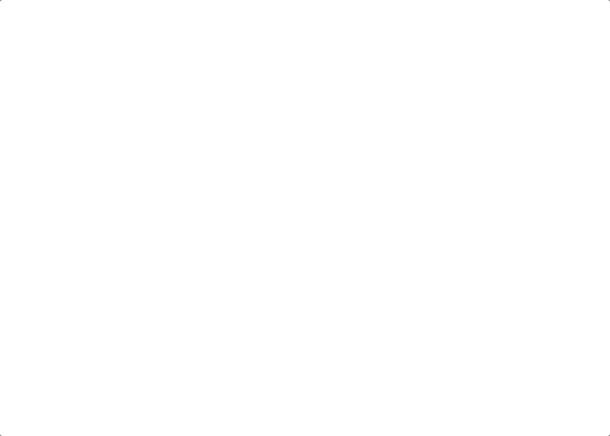
👻方法2:原地反转(双指针法)
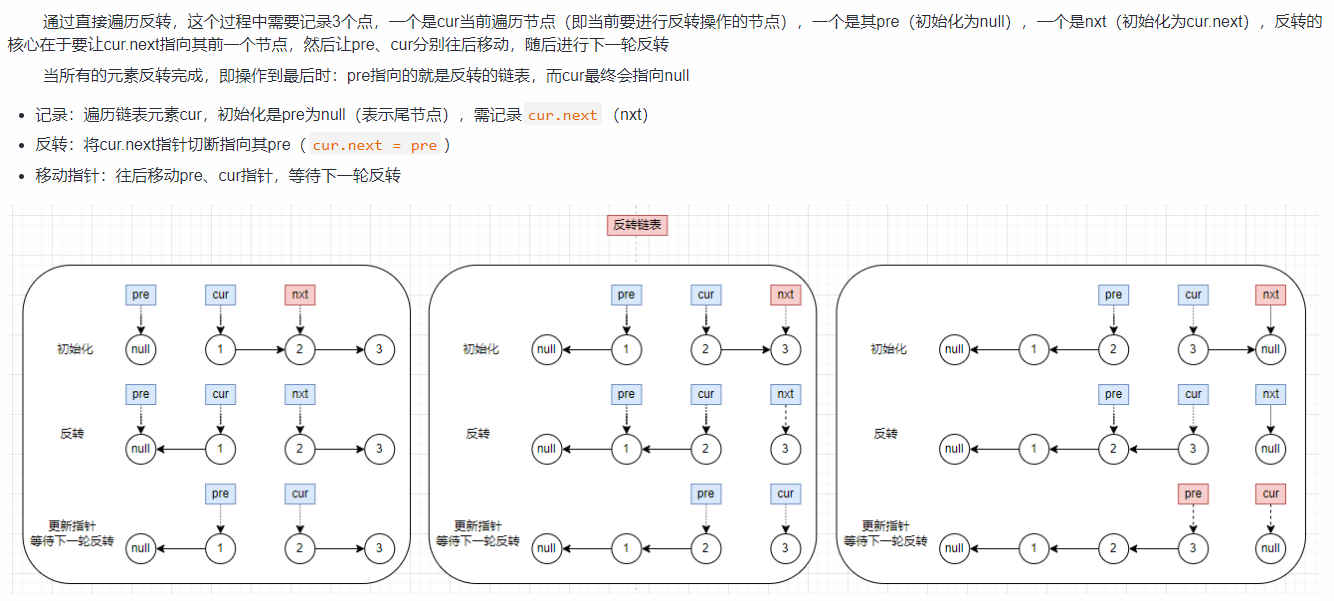
- 思路分析:记录
pre、cur、next,每次遍历让cur.next指向pre,然后让pre、cur向后移动即可- 核心思路实际上就是维护反转后链表的头节点,通过遍历head的每个链表元素,让其next指向当前的pre,则后续pre、cur往前移动
/**
* 206 反转链表
*/
public class Solution3 {
// 原地反转
public ListNode reverseList(ListNode head) {
ListNode pre = null; // 把它当做反转后链表的头节点,遍历head链表依次把链表元素给它加入到pre前
ListNode cur = head;
// 遍历节点依次进行反转
while(cur!=null){
ListNode nxt = cur.next; // 记录
cur.next = pre; // 让 cur.next 指向 pre
// 更改pre、cur(后移),等待下一次遍历
pre = cur;
cur = nxt;
}
return pre; // pre 指向位置就是反转后的链表
}
}
复杂度分析
时间复杂度:O(n)n 为链表节点个数
空间复杂度:O(1)原地交换链表只需要O(1)空间占用
👻思路3:头插(遍历)
- 思路分析:依次遍历元素,然后将节点依次插入到新链表的头部(这种方法思路的优化版本就是【思路2】)
/**
* 206 反转链表
*/
public class Solution4 {
// 遍历+头插
public ListNode reverseList(ListNode head) {
ListNode dummy = null; // 其作为尾节点初始化为null(后面所有元素都会插入到其头部)
ListNode cur = head;
// 遍历节点依次头插
while (cur != null) {
dummy = new ListNode(cur.val, dummy);
cur = cur.next;
}
return dummy; // pre 指向位置就是反转后的链表
}
}
复杂度分析
时间复杂度:O(n)n 为链表节点个数
空间复杂度:O(n)每次构建新节点
🟡092-反转链表II
1.题目内容
给你单链表的头指针 head 和两个整数 left 和 right ,其中 left <= right 。请你反转从位置 left 到位置 right 的链表节点,返回 反转后的链表
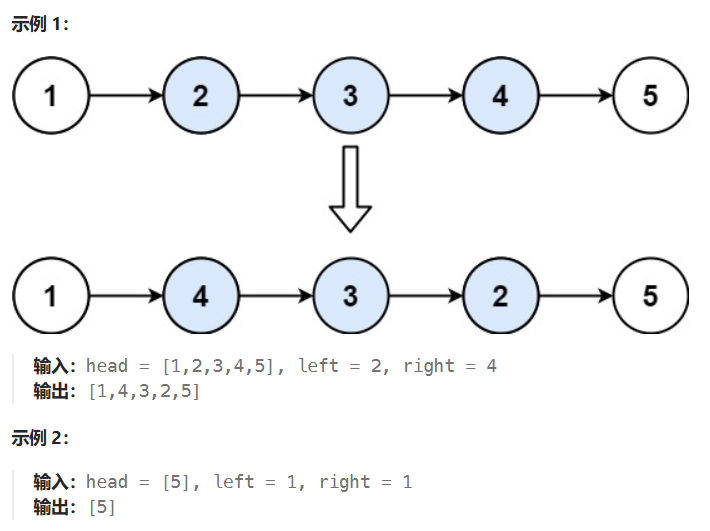
2.题解思路
👻方法1:分段处理(顺序遍历)
- 思路分析:顺序遍历,对指定范围内的节点进行反转处理(此处需构建虚拟头节点来辅助处理)
public class Solution2 {
/**
* 分段处理:
* 第1段:[0,left-1] 正常遍历
* 第2段:[left,right] 反转
* 第3段:[right+1,end] 拼接
*/
public ListNode reverseBetween(ListNode head, int left, int right) {
// 定义虚拟头节点
ListNode dummy = new ListNode(-1, head); // 将head拼接过来构成一个新链表,对这个新链表进行区间反转操作:等价于ListNode dummy = new ListNode(-1); dummy.next = head;
ListNode pd = dummy; // pd指针指向新链表的头节点
/**
* 第1段:正常遍历(p、cur向前移动,到达要进行反转的左区间)
* 遍历完成 pd 的下一个节点指向的是要翻转的节点(因为dummy多了个虚拟头结点)
*/
for (int i = 0; i < left - 1; i++) {
pd = pd.next;
}
/**
* 第2段:反转这个范围区间的链表节点
*/
ListNode pre = null; // 指向前一个节点
ListNode cur = pd.next; // cur 指向当前要反转的节点(当前遍历的节点位置)
for (int i = 0; i < right - left + 1; i++) {
// 记录位置,翻转节点
ListNode nxt = cur.next; // 记录当前要翻转的下一个节点内容(避免被覆盖)
cur.next = pre; // 将cur.next指向前一个节点pre
// 更新指针位置,等待下一轮反转(pre、cur往后移动)
pre = cur;
cur = nxt;
}
// 反转完成最终cur指向的就是反转区间的下一个节点(此处也就是指代第三段区间),而pre则是指向反转完成的这个区间
// 拼接:找到第一段的拼接位置,将反转后的区间和第三段区间进行拼接(此处是先操作pd.next.next,再操作pd.next,避免影响覆盖)
pd.next.next = cur;
pd.next = pre;
return dummy.next;
}
}
复杂度分析
时间复杂度:O(n) n 为链表节点个数
空间复杂度:O(1)占用常数级空间辅助反转
👻方法1:分段处理(分段 + 反转 + 链接)
- 思路分析:
/**
* 🟡 092 反转链表II - https://leetcode.cn/problems/reverse-linked-list-ii/description/
*/
public class Solution1 {
/**
* 分段处理:分段 + 反转 + 重新链接
*/
public ListNode reverseBetween(ListNode head, int left, int right) {
// 构建虚拟头节点,基于dummy遍历寻找要进行反转的区间范围相关节点
ListNode dummy = new ListNode(-1, head);
ListNode cur = dummy;
// 获取开始节点的前一个节点
for (int i = 0; i < left - 1; i++) {
cur = cur.next;
}
ListNode preStartNode = cur; // 记录反转起点的前一个节点
ListNode startNode = cur.next; // 记录反转起点
for (int i = 0; i < right - left + 1; i++) {
cur = cur.next;
}
ListNode endNode = cur; // 记录反转终点
ListNode endNxtNode = cur.next; // 记录反转终点的下一个节点
// ① 断开链表
preStartNode.next = null;
endNode.next = null;
// ② 反转中间段链表
ListNode reverseNode = reverse(startNode);
// ③ 重新链接
preStartNode.next = reverseNode;
startNode.next = endNxtNode; // 范围反转后原起点变为反转后的链表终点,将其和下一段链表链接在一起
// 返回结果
return dummy.next;
}
// 反转链表
private ListNode reverse(ListNode head) {
ListNode pre = null;
ListNode cur = head;
while (cur != null) {
ListNode nxt = cur.next; // 记录下一个节点
cur.next = pre;
// 更新指针
pre = cur;
cur = nxt;
}
// 返回反转后的链表
return pre;
}
}
复杂度分析
时间复杂度:O(n) n 为链表节点个数
空间复杂度:O(1)占用常数级空间辅助反转
🟡024-两两交换链表中的节点
1.题目内容
给你一个链表,两两交换其中相邻的节点,并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题(即,只能进行节点交换)。
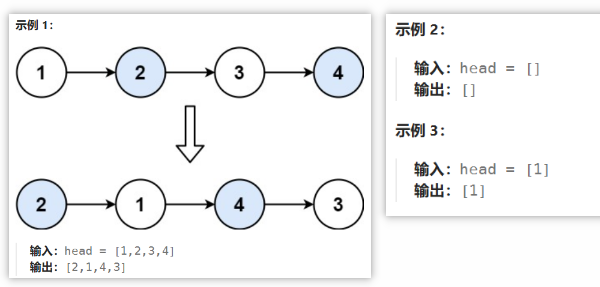
2.题解思路
👻方法1:迭代(两两交换)
思路分析:构建虚拟头节点(可以避免很多麻烦),拼接一个新链表,然后对这个链表进行迭代
- 迭代过程涉及到4个节点:cur、first、second、third 依次标注这些节点,然后思考如何实现两两节点交换(交换目标:fist、second)=》构建虚拟头节点、记录节点、执行交换、指针后移
- (1)记录节点:确定交换涉及到的4个节点,要进行交换的是中间的两个节点
- (2)执行交换:从左到右更新交换后的指针关系(前面记录了每个节点,此处从左到右更新每个节点的next指针,不需要死记硬背)
cur.next = second(cur 节点的下一个节点是 second)second.next = first(紧接着更新second的next节点为first)first.next = third(随后继续更新first的next节点为third)- 基于此完成了fist、second两个节点的两两交换
- (3)指针后移:交换操作完成,指针继续后移,指向下一个待交换的节点
- 易错点:惯性思维可能会认为
cur=cur.next,但实际上此时由于节点已经交换过位置,因此cur.next已经发生了改变,此处应该关注的是下一个要交换的节点是哪个 - 结合图示分析,节点交换后
cur.next已经完成了交换,因此实际上cur移动应该移动到其交换后的下下个节点,也就是fisrt节点(这是交换前的节点记录下的状态)
- 易错点:惯性思维可能会认为
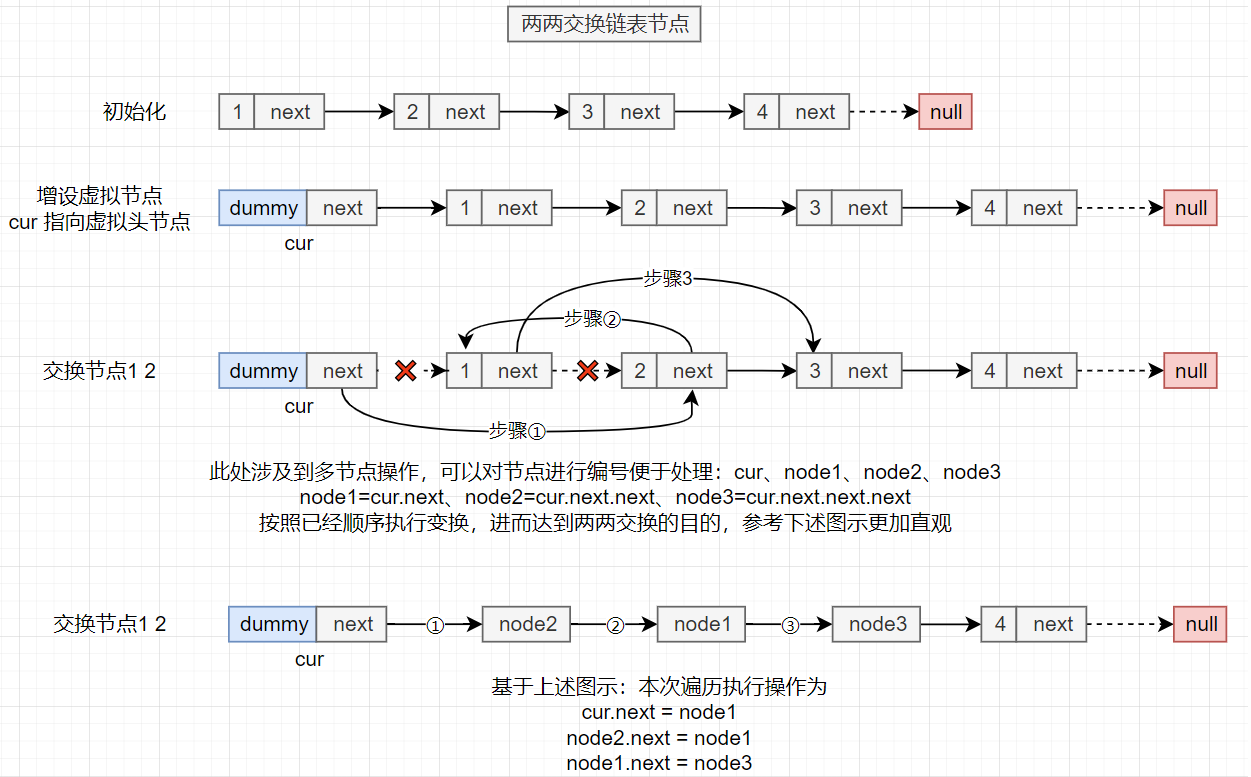
/**
* 024 两两交换链表的节点
*/
public class Solution1 {
// 迭代法
public ListNode swapPairs(ListNode head) {
// 定义虚拟头节点构建链表
ListNode dummy = new ListNode(-1, head);
ListNode cur = dummy; // 遍历指针,指向dummy
// 遍历
while (cur.next != null && cur.next.next != null) {
// 记录节点
ListNode first = cur.next;
ListNode second = first.next;
ListNode third = second.next;
// 交换节点
cur.next = second;
second.next = first;
first.next = third;
// 交换完成,cur指针后移,指向下一个待交换的位置
cur = first; // 结合图示理解,此时应该指向原来的first
}
// 返回链表
return dummy.next;
}
}
复杂度分析
时间复杂度:O(n) n 为链表节点个数
空间复杂度:O(1)交换过程中是O(1)操作,整个过程原地交换,只占用常数级别的空间
🟡019-删除链表的倒数第N个节点
1.题目内容
给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点
2.题解思路
👻方法1:辅助集合(队列或者栈)
链表节点删除技巧:对于链表删除操作,可借助虚拟头节点辅助(可以避免头节点为空的情况判断),但需注意引入头节点时要考虑其对链表长度的影响,在检索第N个或者倒数第N个的时候要注意索引取值的有效范围,去掉这个头节点
思路分析:对于链表删除节点操作,引入dummy虚拟头节点可以避免对头节点的讨论
借助辅助集合完成删除操作,删除操作的目的在于找到待删除节点的前一个节点
栈:正序遍历链表入栈,然后找到倒数第n-1个节点,执行删除操作(
prev.next=prev.next.next)/** * 019 删除链表的倒数第N个节点 */ public class Solution1 { // 迭代:辅助栈(倒数第N个节点,对于栈而言为第N个) public ListNode removeNthFromEnd(ListNode head, int n) { // 辅助栈 Stack<ListNode> stack = new Stack<>(); // 虚拟头节点 ListNode dummy = new ListNode(-1, head); ListNode cur = dummy; // 遍历链表 while (cur != null) { stack.push(cur); cur = cur.next; // 指针后移 } // 遍历栈,找到待删除节点的前一个节点,即栈对应的N-1 for (int i = 0; i < n; i++) { // 因为构建了一个虚拟头节点,因此要弹出N-1个节点,下一个节点才是N-1 stack.pop(); } // 取到倒数第N-1 ListNode prev = stack.peek(); prev.next = prev.next.next; // 执行删除 // 返回链表 return dummy.next; } }队列:正序遍历链表入队列,删除第N个节点即删除队列中的第
L-N+1个节点(L为链表长度),正序遍历找到这个节点的前一个然后执行删除/** * 019 删除链表的倒数第N个节点 */ public class Solution2 { // 迭代:辅助列表(倒数第N个节点,对于队列而言是第L-N+1,注意虚拟头节点的影响) public ListNode removeNthFromEnd(ListNode head, int n) { // 辅助队列(借助列表集合) List<ListNode> queue = new ArrayList<>(); // 虚拟头节点 ListNode dummy = new ListNode(-1, head); ListNode cur = dummy; // 遍历链表 while (cur != null) { queue.add(cur); cur = cur.next; // 指针后移 } // 取到倒数第N-1 ListNode prev = queue.get(queue.size() - n -1); // 因为多加了个虚拟头节点,因此此处要注意取值 prev.next = prev.next.next; // 执行删除 // 返回链表 return dummy.next; } } // 另一种写法 class Solution { public ListNode removeNthFromEnd(ListNode head, int n) { ListNode dummy = new ListNode(0, head); int length = getLength(head); ListNode cur = dummy; for (int i = 1; i < length - n + 1; ++i) { cur = cur.next; } cur.next = cur.next.next; ListNode ans = dummy.next; return ans; } public int getLength(ListNode head) { int length = 0; while (head != null) { ++length; head = head.next; } return length; } }
复杂度分析
时间复杂度:O(n)需遍历所有节点,然后借助辅助集合操作
空间复杂度:O(n)借助辅助集合操作
- 如果要进一步优化空间复杂度,可以考虑用时间换空间的思路,一次遍历计算链表长度,然后根据长度找到
len-n的位置,进一步执行相关操作(如果构建了虚拟头节点,则应找len-n-1的位置才是待删除节点的前置节点)
- 如果要进一步优化空间复杂度,可以考虑用时间换空间的思路,一次遍历计算链表长度,然后根据长度找到
👻方法2:快慢指针
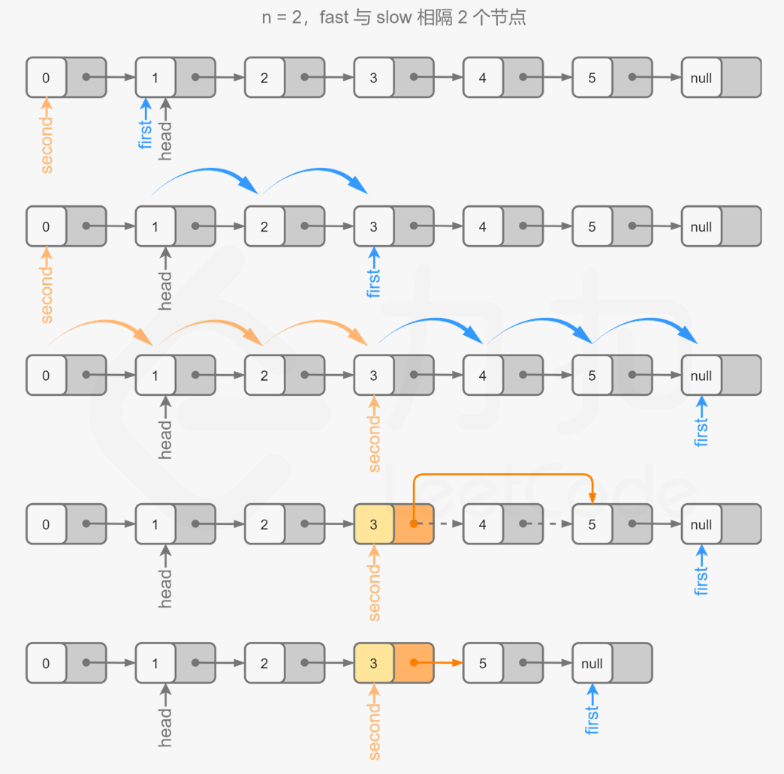
- 思路分析:快指针先走N步停下,然后慢指针(起点为dummy头节点)和快指针(起点为head第N个元素)再同时出发(慢指针和快指针始终相差N+1,),当快指针到达终点的时候,此时慢指针指向的位置就是删除位置(待删除节点的前置节点)
- 巧妙利用快慢指针的思路(如果概念懵最好的解决方式就是画图/举例理解)
- 举例分析:
[1,2,3,4,5]=》[-1,1,2,3,4,5](n==2)- (1)初始化指针:
slow指向-1(即dummy),fast指向节点1(head,即dummy.next) - (2)
fast先走 n 步,到达节点3 - (3)随后
slow、fast同时出发,当fast到达尾节点null(此处是遍历到尾节点,而不是节点5)时,此时slow到达节点3
- (1)初始化指针:
- 实现分析:对于链表
head定义快慢指针用于遍历- (1)初始化指针:
slow初始化指向dummy、fast初始化指向head(即dummy.next) - (2)
fast指针先走n步 - (3)随后
slow、fast同时出发,当fast到达链表尾部的时候,此时slow也到达了第len-n的位置(也就是要删除的倒数第N个节点)
- (1)初始化指针:
- 进一步说明:由于删除节点是要找到待删除节点的前驱节点
prev(然后直接执行prev.next=prev.next.next),因此此处如果slow能再晚一步出发,那么等到fast到达链表尾部的时候slow刚好就到达这个待删除的倒数第N个节点的前驱节点位置。因此dummy虚拟头节点就派上用场了,引入dummy=new ListNode(-1,head),让slow初始化指向dummy那么就能达到目的- 此处虚拟头节点的引入有两个好处:
- 不用考虑删除头节点的各种判断的苦恼(避免头节点
NPE问题处理繁琐) - 让slow再慢一步出发(slow起点为dummy),能够拿到待删除节点的前驱节点,更好地进行删除操作
- 不用考虑删除头节点的各种判断的苦恼(避免头节点
- 此处虚拟头节点的引入有两个好处:
- 举例分析:
- 巧妙利用快慢指针的思路(如果概念懵最好的解决方式就是画图/举例理解)
/**
* 🟡019 删除链表的倒数第N个节点
*/
public class Solution019_03 {
/**
* 思路:快慢指针
* 快指针先走N步,然后快慢指针同时出发,当快指针走到终点,此时慢指针指向位置就是删除位置
*/
public ListNode removeNthFromEnd(ListNode head, int n) {
// 构建虚拟头节点
ListNode dummy = new ListNode(-1, head);
ListNode slow = dummy, fast = head;
// 快指针出发先走N步
while (n-- > 0) {
fast = fast.next;
}
// 快慢指针同时出发(快指针和慢指针始终相差N+1)
while (fast != null) {
slow = slow.next;
fast = fast.next;
}
// 慢指针位置为删除位置
slow.next = slow.next.next;
// 返回结果
return dummy.next;
}
}
复杂度分析
时间复杂度:O(n)需遍历所有节点,然后借助辅助集合操作(此处分别定义快、慢指针遍历链表)
- 空间复杂度:O(1)此处构建了快慢指针进行遍历
🟢160-链表相交
1.题目内容
给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表没有交点,返回 null 。
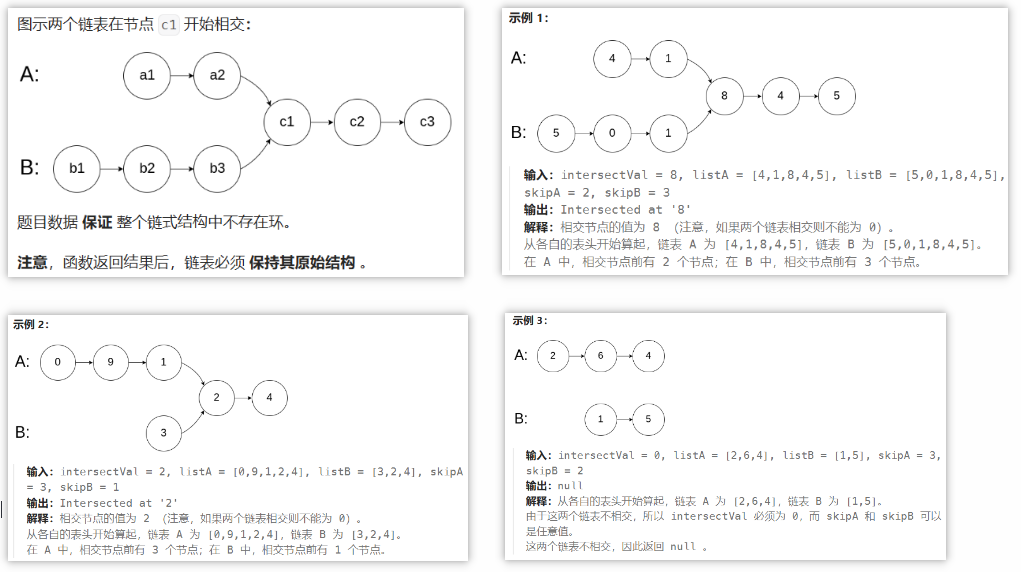
2.题解思路
👻方法1:双指针迭代
思路分析
如果两个链表相交则其存在公共节点,则可以定义两个指针分别从A、B链表头节点出发分别同时完成两个链表的遍历
pointerA(遍历方向:A->B):一直遍历A链表,如果A链表遍历完成则接着遍历B链表pointerB(遍历方向:B->A):一直遍历B链表,如果A链表遍历完成则接着遍历A链表为什么循环退出的条件是
pointerA==pointerB,此处讨论两种情况:- A B 链表不存在公共交点,则
pointerA和pointerB会同时到达尾节点null(因为A+B=B+A,同时出发,同时结束) - A B 链表存在公共交点:假设A、B链表存在公共节点,基于两个指针同时出发,结合下图可以列出公式
- a + (b - c) 表示
pointerA走完了A链表,然后继续遍历B链表走了b-c步骤到达公共节点 - b + (a - c) 表示
pointerB走完了B链表,然后继续遍历A链表走了a-c步骤到达公共节点 - 数学公式上
a + (b - c) = b + (a - c)是一定会成立的,也就是说如果两个指针同时遍历A、B的话最终一定会指向一个节点(也就是循环退出的条件会达到),这个节点必定是公共节点(只不过此处的公共节点概念是:如果node为null表示尾指针四舍五入不存在,如果node不为null表示存在公共节点)
- a + (b - c) 表示

- A B 链表不存在公共交点,则
/**
* 160 相交链表
*/
public class Solution1 {
// 双指针思路
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
// 边界条件判断
if (headA == null || headB == null) {
return null;
}
// 分别定义两个指针执行遍历操作:A->B、B->A链表
ListNode pointerA = headA;
ListNode pointerB = headB;
while (pointerA != pointerB) {
// A 链表遍历
if (pointerA != null) {
pointerA = pointerA.next;
} else {
// 如果遍历到A链表尾部,则切到B链表
pointerA = headB;
}
// B 链表遍历
if (pointerB != null) {
pointerB = pointerB.next;
} else {
// 如果遍历到B链表尾部,则切到A链表
pointerB = headA;
}
}
return pointerA;
}
}
复杂度分析
时间复杂度:O(m+n)需要遍历两个链表的节点,最坏情况下会遍历完所有链表节点(两个链表无交点或者遍历到最后)
空间复杂度:O(1)
👻方法2:哈希表(固定一个链表到哈希表+遍历另一个链表判断节点是否存在于哈希集合中)
- 思路分析
- 判断是否存在公共节点,本质上就是判断两个链表有没有相同的val,最硬核的做法就是遍历两个链表,此处借助哈希表实现(固定一个链表存储到哈希表,然后遍历另一个链表判断节点是否存在于哈希集合中)
/**
* 160 相交链表
*/
public class Solution2 {
// 哈希表(固定某个链表的所有元素到哈希表,随后遍历另一个链表判断是否存在交点)
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
// 定义哈希表
Set<ListNode> setA = new HashSet<>();
// 遍历链表A,将节点载入setA
ListNode pointerA = headA;
while(pointerA!=null){
setA.add(pointerA);
pointerA = pointerA.next;
}
// 遍历链表B,判断是否存在交点
ListNode pointerB = headB;
while(pointerB!=null){
if(setA.contains(pointerB)){ // 存在交点
return pointerB;
}else{
// 指针后移继续往下找
pointerB = pointerB.next;
}
}
// 无交点
return null;
}
}
复杂度分析
时间复杂度:O(m+n)需遍历连个链表
空间复杂度:O(m)需借助辅助set存储某个链表的集合
👻方法2:双指针(快慢指针:fast先走n步,然后slow、fast同时出发)
- 思路分析:巧妙利用快慢指针的思路
- 实现分析:对于链表
head定义快慢指针,slow、fast初始化指向head- (1)
fast指针先走n步 - (2)随后
slow、fast同时出发,当fast到达链表尾部的时候,此时slow也到达了第len-n的位置(也就是要删除的倒数第N个节点)
- (1)
- 进一步说明:由于删除节点是要找到待删除节点的前驱节点
prev(然后直接执行prev.next=prev.next.next),因此此处如果slow能再晚一步出发,那么等到fast到达链表尾部的时候slow刚好就到达这个待删除的倒数第N个节点的前驱节点位置。因此dummy虚拟头节点就派上用场了,引入dummy=new ListNode(-1,head),让slow初始化指向dummy那么就能达到目的- 此处虚拟头节点的引入有两个好处:
- 不用考虑删除头节点的各种判断的苦恼(避免头节点NPE处理繁琐)
- 让slow再慢一步出发,能够拿到待删除节点的前驱节点,更好地进行删除操作
- 此处虚拟头节点的引入有两个好处:
- 实现分析:对于链表
/**
* 019 删除链表的倒数第N个节点
*/
public class Solution019 {
/**
* 双指针:定义快慢指针
* 1.快指针从head开始,让快指针先走n步 慢指针从起点(dummy)开始
* 2.当快指针走了n步之后,双指针同时出发,当快指针走到链表尾部的时候此时慢指针恰好就走到倒数第n个节点
*/
public ListNode removeNthFromEnd(ListNode head, int n) {
// 构建虚拟头节点
ListNode dummy = new ListNode(-1, head);
// 定义双指针
ListNode slow = dummy, fast = head; // slow初始指向dummy(是为了拿到待删除节点的前驱节点),fast初始指向head
// 1.快指针先走n步
for (int i = 0; i < n; i++) {
fast = fast.next;
}
// 2.双指针再一起出发,当快指针遍历到链表尾部,此时慢指针指向len-n(倒数第n的位置)的前驱节点位置
while (fast != null) {
slow = slow.next;
fast = fast.next;
}
// 删除指定节点
slow.next = slow.next.next;
// 返回
return dummy.next;
}
}
复杂度分析
时间复杂度:O(n)双指针遍历链表,当fast遍历到链表尾部循环结束
空间复杂度:O(1)只占用常数级别的空间
🟡142-环形链表II
1.题目内容
给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递,仅仅是为了标识链表的实际情况。
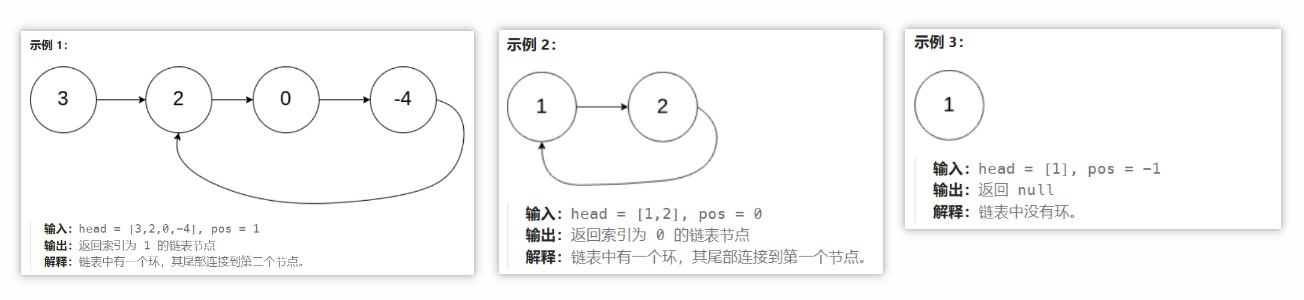
链表问题:结合图示理解算法的设计,哈希表、双指针,画图理解
2.题解思路(环形链表I 141)
👻方法1:快慢指针(判断是否存在环)
- 思路分析:141 环形链表(判断是否存在环)可以通过快慢指针来实现(龟兔赛跑:起点相同,慢指针走1步,快指针走两步,如果存在环则会相遇)
/**
* 141 环形链表
*/
public class Solution1 {
// 快慢指针思路:龟兔赛跑
public boolean hasCycle(ListNode head) {
// null 判断
if (head == null) {
return false;
}
ListNode slow = head;
ListNode fast = head;
// 当fast先走到终点(null)则跳出循环
while (fast != null && fast.next != null) { // 如果不存在环则快指针会到达终点,如果存在环则一直转圈圈
// 指针后移(先走后判断,起点相同(如果先判断则逻辑错误了))
slow = slow.next; // 龟走1步
fast = fast.next.next; // 兔子走两步
// 如果这个过程中两个指针相遇,说明存在环
if (slow == fast) { // 兔子追上龟(套圈)
return true;
}
}
return false; // fast访问到了链表末尾,说明无环
}
}
复杂度分析
时间复杂度:O(n)n 为链表节点个数
空间复杂度:O(1)双指针
👻方法2:哈希表
- 思路分析:141 环形链表(判断是否存在环)可以通过哈希表来实现,将已经遍历过的节点载入集合,每次遍历的时候判断cur.next是否已经被遍历过,如果被遍历过则说明存在环,没有则加入集合并继续下一个元素判断
/**
* 141 环形链表
*/
public class Solution2 {
// 哈希表
public boolean hasCycle(ListNode head) {
if(head==null){
return false;
}
// Set存储已遍历元素
Set<ListNode> visited = new HashSet<>();
// 遍历链表,判断cur.next是否已经被访问过
ListNode cur = head;
while(cur!=null){
if(visited.contains(cur.next)){
return true;
}
visited.add(cur); // 将当前指针放入visited集合
cur = cur.next; // 指针后移,继续下一个元素判断
}
// 所有节点遍历完成,说明不存在环
return false;
}
}
复杂度分析
时间复杂度:O(n)n 为链表节点个数
空间复杂度:O(n)需要借助集合维护已遍历元素
3.题解思路(环形链表II 142)
👻方法1:哈希表
此处和环形链表I中的解法类似,只不过此处不是校验cur.next是否已经出现在集合中,而是基于遍历线性链表的思路(可以理解为将链表平展概念),如果发现遍历元素cur已经出现在集合中则说明存在环,且这个环的入口就是cur
此处将下述代码的return条件转化为boolean即为【141-判断链表是否有环】的题解。但是如果此处校验的如果是cur.next(可能存在问题,此处还是选用cur校验的思路去做,吃透两道题目即可,不去绕圈圈)
/**
* 🟡 142 环形链表II
*/
public class Solution142_01 {
/**
* 思路:哈希表
* 构建辅助集合存储已遍历元素,如果遍历节点重复出现则说明链表存在环
*/
public ListNode detectCycle(ListNode head) {
// 特例判断
if (head == null) {
return head;
}
// 构建辅助集合存储已遍历元素
Set<ListNode> set = new HashSet<>();
// 遍历链表
ListNode cur = head;
while (cur != null) {
if (set.contains(cur)) {
return cur; // cur为入环节点
}
set.add(cur);
cur = cur.next;
}
return null;
}
}
// ---------- 写法2 ----------
/**
* 🟡 142 环形链表II - https://leetcode.cn/problems/linked-list-cycle-ii/
*/
public class Solution142_02 {
/**
* 思路:哈希表
*/
public ListNode detectCycle(ListNode head) {
// 定义哈希表存储已遍历元素
HashMap<ListNode, ListNode> map = new HashMap<>();
ListNode cur = head;
while (cur != null) {
if (map.containsKey(cur.next)) {
// return cur;
// return map.get(cur.next); // 此处要返回环入口,因此返回的是map集合中的元素
return cur.next; // 两个指向同一个元素也可用set存储,返回的是cur.next
}
map.put(cur, cur);
cur = cur.next;
}
// 不存在环
return null;
}
}
👻方法2:快慢指针(判断是否存在环、返回入环的节点)
- 思路分析:142 环形链表(判断是否存在环,返回入口)可以通过哈希表来实现,将已经遍历过的节点载入集合,每次遍历的时候判断cur.next是否已经被遍历过,如果被遍历过则说明存在环(如果存在环说明指向同一个节点,因此此处直接返回这个入口即可cur.next 如果要返回索引位置则借助 List 根据指定节点的索引位置),没有则加入集合并继续下一个元素判断
/**
* 142 环形链表II
*/
public class Solution1 {
// 快慢指针思路:龟兔赛跑(先判断是否存在环,如果存在环则继续下一步寻找入口)
public ListNode detectCycle(ListNode head) {
// null 判断
if (head == null) {
return null;
}
// 龟兔赛跑起点相同
ListNode slow = head;
ListNode fast = head;
// 找到指针相遇的点
while (true) {
// 当fast先走到终点(null)则跳出循环
if (fast == null || fast.next == null) {
return null; // 如果fast指针可以遍历到尾部说明不存在环,直接return null
}
// 指针后移
slow = slow.next;
fast = fast.next.next;
// 如果这个过程中两个指针相遇,说明存在环
if (slow == fast) {
break; // 如果存在环,则跳出当前循环
}
}
// 如果执行到此步骤,说明链表存在环,则进一步寻找环的入口
fast = head; // 让fast从头开始走
while (slow != fast) { // 既然明确存在环,则让fast从头节点出发,slow从当前位置出发,一起走总会相遇,相遇点即为环入口
slow = slow.next;
fast = fast.next;
}
return fast; // 此时两者相遇即入口,返回slow和fast均可
}
}
// 写法参考
/**
* 🟡 142 环形链表II
*/
public class Solution142_03 {
/**
* 思路:双指针思路
* 龟兔赛跑,判断是否存在环,如果存在环则继续寻找环的入口
*/
public ListNode detectCycle(ListNode head) {
if (head == null) {
return null;
}
// 定义快慢指针
ListNode slow = head, fast = head;
// 判断是否存在环,如果存在环则从相遇点跳出
boolean hasCycle = false;
while (fast != null && fast.next != null) {
slow = slow.next; // 慢指针走1步
fast = fast.next.next; // 快指针走2步
if (slow == fast) {
// 如果快慢指针相遇则存在环
hasCycle = true;
break; // 相遇则跳出
}
}
// 判断是否存在环,如果存在则继续寻找环的入口
if (!hasCycle) {
return null; // 不存在环,直接退出
}
// 存在环,继续寻找环的入口(定义指针cur从起点出发,与相遇点slow同步前进,两者相遇的点即为环的入口)
ListNode cur = head; // 此处也可以复用fast指针空间,为了区别作用定义了cur指针
while (cur != slow) {
cur = cur.next;
slow = slow.next;
}
// 返回环的起点(入环口)
return cur;
}
}
复杂度分析
时间复杂度:O(n)n 为链表节点个数
空间复杂度:O(1)借助双指针实现
🟢234-回文链表
1.题目内容
给你一个单链表的头节点 head ,请你判断该链表是否为回文链表。如果是,返回 true ;否则,返回 false 。
2.题解思路
首先理解对于"回文"的求解,例如回文字符串的求解,最基础的就是正着读和反着读序列完全一致,还有双指针法校验等
👻方法1:辅助集合 + 双指针校验
- 思路分析:读取链表元素到指定集合,然后基于双指针法校验回文
/**
* 🟢234 回文链表
*/
public class Solution1 {
/**
* 辅助集合 + 双指针校验回文
*/
public boolean isPalindrome(ListNode head) {
// 定义辅助集合存储链表值
List<Integer> list = new ArrayList<>();
// 遍历链表
ListNode cur = head;
while (cur != null) {
list.add(cur.val);
cur = cur.next;
}
// 校验回文(双指针)
int start = 0, end = list.size() - 1;
while (start <= end) {
if (list.get(start) != list.get(end)) {
return false; // 非回文
}
// 继续下一个校验
start++;
end--;
}
// 校验通过
return true;
}
}
复杂度分析
时间复杂度:O(n)需遍历链表读取数值到集合,然后基于双指针校验回文
空间复杂度:O(n)n为链表节点个数,需构建辅助集合存储链表元素
👻方法2:辅助栈 + 正读/反读序列一致(读一半即可)
- 思路分析:
- 第1次遍历链表:将链表元素依次入栈
- 第2次遍历链表:再次遍历链表并依次与栈弹出的元素比较是否匹配(正序=反序,只需要检验一半的元素即可)
/**
* 🟢234 回文链表
*/
public class Solution2 {
/**
* 辅助栈 + 正序反序校验(校验一半的元素)
*/
public boolean isPalindrome(ListNode head) {
// 定义辅助栈存储链表元素
Stack<Integer> stack = new Stack<>();
// 遍历链表
ListNode cur = head;
while (cur != null) {
stack.push(cur.val);
cur = cur.next;
}
// 再次遍历链表(正序)与栈中元素(逆序)一一校验,此处只需要校验一半的元素即可
int cnt = stack.size() / 2;
ListNode pointer = head; // 遍历指针
for (int i = 0; i < cnt; i++) {
if (pointer.val != stack.pop()) {
return false;
}
pointer = pointer.next; // 指针后移,继续遍历下一位元素
}
// 校验通过
return true;
}
}
复杂度分析
时间复杂度:O(n)需遍历链表读取数值到栈,然后再遍历一遍链表依次与栈中弹出的元素进行匹配
空间复杂度:O(n)n为链表节点个数,需构建辅助集合存储链表元素
🟡143-重排链表
1.题目内容
给定一个单链表 L 的头节点 head ,单链表 L 表示为:
L0 → L1 → … → Ln - 1 → Ln
请将其重新排列后变为:
L0 → Ln → L1 → Ln - 1 → L2 → Ln - 2 → …
不能只是单纯的改变节点内部的值,而是需要实际的进行节点交换。
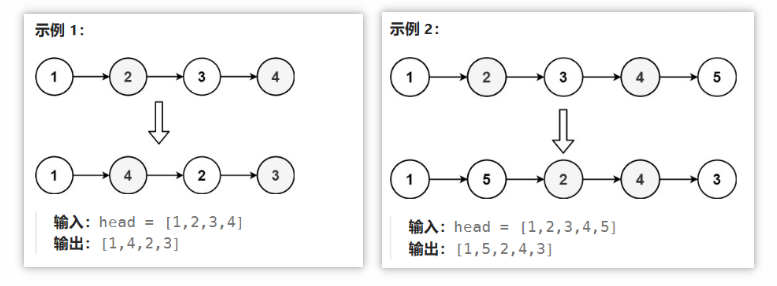
2.题解思路
👻方法1:辅助集合 + 双指针遍历构造
- 思路分析:遇到链表的题型,本质上是不同数据结构的数据处理,很多题型是换汤不换药,要思考如果借助链表的特性来达到处理的目的,如果难以操作则借助辅助集合进行处理即可。此处结合题意分析,本质上是遍历链表,只不过此处穿插交替头尾遍历。因此可以借助集合辅助遍历
- ① 第1次遍历:将所有链表节点加入
list,于此同时也得到了链表长度 - ② 第2次处理:基于链表长度重新构建链表,这种头尾交替遍历的方式可以借助两个指针来处理(指针分别从头尾出发)
- 当
i为偶数则取正序遍历的指针指向节点 - 当
i为奇数则取逆序遍历的指针指向节点
- 当
- ① 第1次遍历:将所有链表节点加入
public void reorderList(ListNode head) {
List<ListNode> list = new ArrayList<>();
// 将链表节点装配到集合中进行处理
ListNode cur = head;
while (cur != null) {
list.add(cur);
cur = cur.next;
}
ListNode dummy = new ListNode(-1);
ListNode pointer = dummy; // 定义指针指向dummy
// 分别定义遍历指针用于从两个方向读取list的节点元素
int leftIdx = 0, rightIdx = list.size() - 1;
for (int i = 0; i < list.size(); i++) {
if (i % 2 == 0) {
// 偶数位置依次填充正序遍历的节点
pointer.next = list.get(leftIdx);
pointer = pointer.next;
leftIdx++;
} else if (i % 2 == 1) {
// 奇数位置依次填充逆序遍历的节点
pointer.next = list.get(rightIdx);
pointer = pointer.next;
rightIdx--;
}
}
pointer.next = null; // handle Error - Found cycle in the ListNode
// 返回结果
// return dummy.next;
head = dummy.next;
}
}
复杂度分析
时间复杂度:O(n)一次遍历链表,一次处理链表并返回
空间复杂度:O(n)需借助集合辅助链表的遍历和处理,在处理阶段可以在原链表上进行操作,也可构建一个
dummy逐步构建新链表
👻方法2:双向队列
- 思路分析:借助双向队列操作(和【方法1】类似,只不过此处用双向队列就不需要自己维护双指针)需注意双向队列的队头、队尾的处理
/**
* 🟡143 重排链表
*/
public class Solution2 {
// 双向队列
public void reorderList(ListNode head) {
// 构建双向队列存储链表节点
Deque<ListNode> deque = new LinkedList<>();
// 遍历链表,入队
ListNode cur = head;
while (cur != null) {
deque.offerLast(cur); // 插入队尾
cur = cur.next;
}
// 根据队列大小填充新链表
ListNode dummy = new ListNode(-1);
ListNode pointer = dummy; // 定义指针指向dummy
int curSize = deque.size(); // deque在遍历的过程中会取出元素,因此要先记录实际的链表节点个数
for (int i = 0; i < curSize; i++) {
if (i % 2 == 0) {
// 偶数(取队头)
pointer.next = deque.pollFirst();
pointer = pointer.next;
} else if (i % 2 == 1) {
// 奇数(取队头)
pointer.next = deque.pollLast();
pointer = pointer.next;
}
}
pointer.next = null; // handle [Error - Found cycle in the ListNode]
head = dummy.next;
}
public static void main(String[] args) {
ListNode node1 = new ListNode(1);
ListNode node2 = new ListNode(2);
ListNode node3 = new ListNode(3);
ListNode node4 = new ListNode(4);
node1.next = node2;
node2.next = node3;
node3.next = node4;
Solution2 s = new Solution2();
s.reorderList(node1);
}
}
复杂度分析
时间复杂度:O(n)一次遍历链表加载到双向队列中,随后依次遍历处理链表节点
空间复杂度:O(n)定义双向队列辅助处理
👻方法3:求中点 + 后半部分反转 + 合并链表
这个思路虽然复杂一点,但也基本覆盖了链表的基本操作题型:双指针求中点、链表反转、合并链表,适合练手
思路分析:这种做法不借助辅助的集合操作,完全在链表上进行操作,需注意细节处理
- ① 求中点(基于快慢指针),链表被拆分为
left、right - ② 将后半部分的链表进行反转得到
reverseRight - ③将前半部分的链表
left与反转后的链表reverseRight进行两两合并
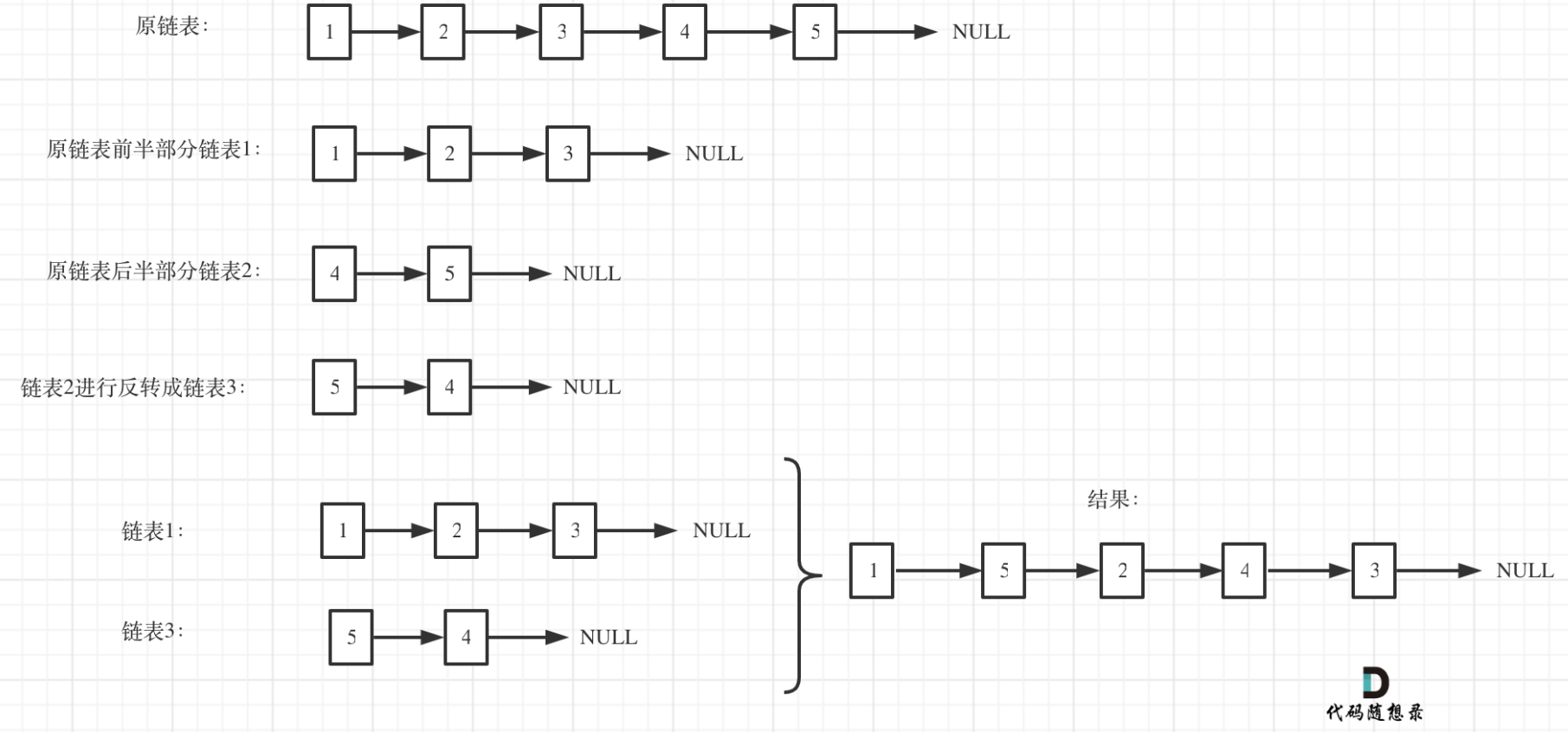
- ① 求中点(基于快慢指针),链表被拆分为
/**
* 🟡143 重排链表
*/
public class Solution3 {
// 求中点 + 后半部分反转 + 合并链表
public void reorderList(ListNode head) {
// ① 求中点(基于快慢指针)
ListNode slow = head, fast = head;
while (fast != null && fast.next != null) {
slow = slow.next;
fast = fast.next.next;
}
// 当fast走到终点,slow位置此时对应为中点位置
ListNode right = slow.next;
slow.next = null; // 将终点位置断开,此时head就是前半部分的链表
ListNode left = head; // 此处为了区分,用left接收
// ② 后半部分反转(对right链表进行反转)
ListNode pre = null;
ListNode cur = right;
while (cur != null) {
ListNode nxt = cur.next; // 记录cur指向的下一个节点
cur.next = pre; // 更改cur.next指针
// 指针滚动更新,等待下一轮处理
pre = cur;
cur = nxt;
}
// ③ 合并链表(将left部分和反转后的right部分合并)
ListNode dummy = new ListNode(-1);
ListNode pd = new ListNode(-1);
ListNode pointerL = left;
ListNode pointerR = pre; // 此处pre对应为反转后的right链表
int idx = 0;
while (pointerL != null && pointerR != null) {
if (idx % 2 == 0) {
pd.next = pointerL;
pd = pd.next;
pointerL = pointerL.next;
idx++;
} else if (idx % 2 == 1) {
pd.next = pointerR;
pd = pd.next;
pointerR = pointerR.next;
idx++;
}
}
if (pointerL != null) {
pd.next = pointerL; // 直接拼接
}
if (pointerR != null) {
pd.next = pointerR; // 直接拼接
}
// pd.next = null;
// 处理结果
head = dummy.next;
}
}
复杂度分析
时间复杂度:O(n)找中点、O(n/2)反转链表、O(n)拼接两个链表
空间复杂度:O(n)需借助指针辅助操作(常数级别),但在合并链表的时候定义了
dummy构建新节点(此处可以直接调整为用head操作,节省空间)
🔴023-合并K个升序链表
1.题目内容
给你一个链表数组,每个链表都已经按升序排列。
请你将所有链表合并到一个升序链表中,返回合并后的链表。
示例 1:
输入:lists = [[1,4,5],[1,3,4],[2,6]]
输出:[1,1,2,3,4,4,5,6]
解释:链表数组如下:
[
1->4->5,
1->3->4,
2->6
]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6
示例 2:
输入:lists = []
输出:[]
示例 3:
输入:lists = [[]]
输出:[]
2.题解思路
👻方法1:两两合并(顺序合并)
- 思路:基于两两合并的思路,可以依次遍历进行顺序合并,也可以每两个一组进行合并随后将合并后的序列再进行两两归并
- 此处【顺序合并】的概念在于用一个变量
base维护合并的链表,依次循环遍历将链表合并后更新base
- 此处【顺序合并】的概念在于用一个变量
/**
* 🔴 023 合并K个升序链表 - https://leetcode.cn/problems/merge-k-sorted-lists/description/
*/
public class Solution1 {
/**
* 思路:两两合并后归并
*/
public ListNode mergeKLists(ListNode[] lists) {
if (lists == null || lists.length == 0) {
return null;
}
ListNode base = lists[0];
for (int i = 1; i < lists.length; i++) {
ListNode newList = mergeTwoList(base, lists[i]); // 两两合并
base = newList; // 更新base作为下一次合并基础
}
// 返回最终合并的结果
return base;
}
/**
* 两两合并链表
*/
public ListNode mergeTwoList(ListNode l1, ListNode l2) {
ListNode dummy = new ListNode(-1);
ListNode cur = dummy;
// 定义指针分别遍历l1、l2
ListNode pointer1 = l1;
ListNode pointer2 = l2;
while (pointer1 != null && pointer2 != null) {
// 比较值的大小,选择较小的一边
if (pointer1.val <= pointer2.val) {
cur.next = new ListNode(pointer1.val);
// 指针移动
cur = cur.next;
pointer1 = pointer1.next;
} else {
cur.next = new ListNode(pointer2.val);
// 指针移动
cur = cur.next;
pointer2 = pointer2.next;
}
}
// 判断是否有剩余尾巴,直接拼接
if (pointer1 != null) {
cur.next = pointer1;
}
if (pointer2 != null) {
cur.next = pointer2;
}
// 返回构建的新链表
return dummy.next;
}
}
复杂度分析
时间复杂度:
- O(m × n) m 个链表 ,每个链表长度不等,
m × n表示链表节点个数;在此基础上还需考虑合并的问题,每次合并都要遍历一遍base链表(也就是说一些链表元素会被重复遍历处理)
- O(m × n) m 个链表 ,每个链表长度不等,
空间复杂度:此处需借助辅助链表
base始终存储合并后的新链表,作为下一次合并的基础
👻方法2:两两合并(分治合并)
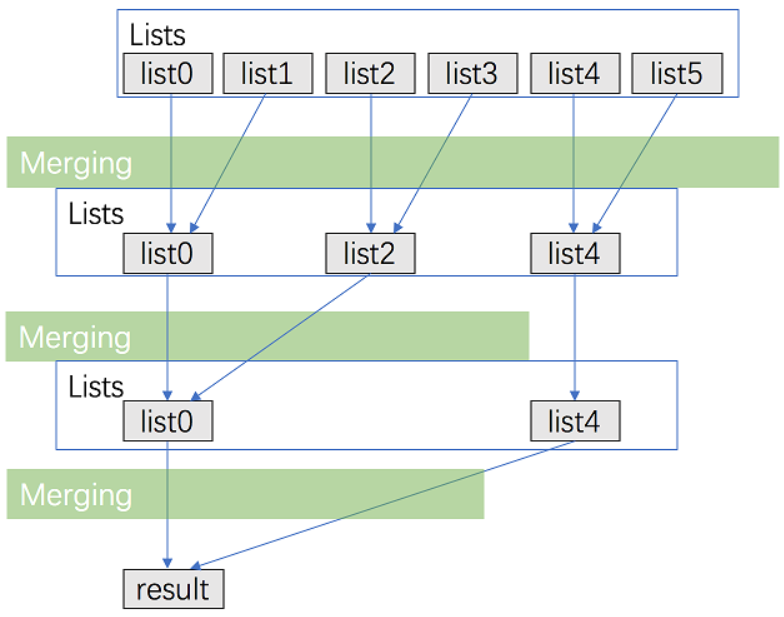
- 思路分析:基于【方法1】进行优化,用分治的方法进行合并
- 将 k 个链表配对并对同一对中的链表进行合并
- 重复合并过程,直到得到最终的有序链表
/**
* 🔴 023 合并K个升序链表 - https://leetcode.cn/problems/merge-k-sorted-lists/description/
*/
public class Solution2 {
/**
* 思路:两两合并后归并
*/
public ListNode mergeKLists(ListNode[] lists) {
return merge(lists, 0, lists.length - 1);
}
/**
* 分组归并
*/
public ListNode merge(ListNode[] lists, int l, int r) {
if (l == r) {
return lists[l];
}
if (l > r) {
return null;
}
int mid = (l + r) >> 1;
return mergeList(merge(lists, l, mid), merge(lists, mid + 1, r));
}
/**
* 两两合并链表
*/
public ListNode mergeList(ListNode l1, ListNode l2) {
ListNode dummy = new ListNode(-1);
ListNode cur = dummy;
// 定义指针分别遍历l1、l2
ListNode pointer1 = l1;
ListNode pointer2 = l2;
while (pointer1 != null && pointer2 != null) {
// 比较值的大小,选择较小的一边
if (pointer1.val <= pointer2.val) {
cur.next = new ListNode(pointer1.val);
// 指针移动
cur = cur.next;
pointer1 = pointer1.next;
} else {
cur.next = new ListNode(pointer2.val);
// 指针移动
cur = cur.next;
pointer2 = pointer2.next;
}
}
// 判断是否有剩余尾巴,直接拼接
if (pointer1 != null) {
cur.next = pointer1;
}
if (pointer2 != null) {
cur.next = pointer2;
}
// 返回构建的新链表
return dummy.next;
}
}
复杂度分析
时间复杂度:
空间复杂度:
👻方法3:基于优先队列合并
- 思路分析:因为每个链表都已经有序,因此可以维护k个元素的小顶堆用于存储k个链表的最小节点,每次取出的时候直接取出最小节点
node,随后将node.next重新入堆等待下一次选择即可
/**
* 🔴 023 合并K个升序链表 - https://leetcode.cn/problems/merge-k-sorted-lists/description/
*/
public class Solution3 {
/**
* 思路:基于优先队列思路,维护k个元素的小顶堆
* - 取出:每次取出一个元素node(最小堆的堆顶元素)
* - 入堆:选出node入队,将node.next重新入堆
*/
public ListNode mergeKLists(ListNode[] lists) {
// 构建优先队列辅助存储
PriorityQueue<ListNode> priorityQueue = new PriorityQueue<>(
new Comparator<ListNode>() {
@Override
public int compare(ListNode o1, ListNode o2) {
return o1.val - o2.val;
}
}
);
// 将集合链表依次入队
for (ListNode node : lists) {
if (node != null) {
priorityQueue.offer(node);
}
}
ListNode dummy = new ListNode(-1);
ListNode cur = dummy;
// 遍历队列
while (!priorityQueue.isEmpty()) {
ListNode node = priorityQueue.poll();
ListNode nxt = node.next;
// 拼接新链表
node.next = null; // 断开连接
cur.next = node;
cur = cur.next;
// 将nxt节点入堆
if (nxt != null) {
priorityQueue.offer(nxt);
}
}
// 返回构建的新链表
return dummy.next;
}
}
复杂度分析
时间复杂度:
空间复杂度:
🟢876-链表的中间结点
1.题目内容
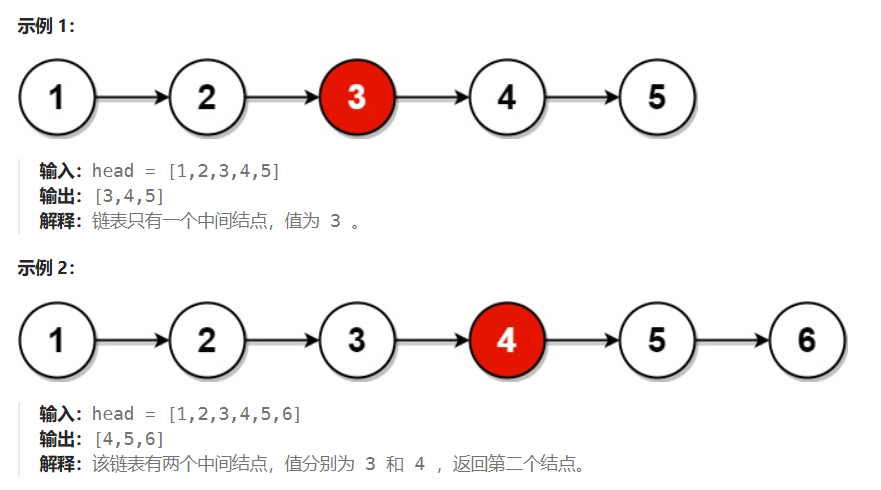
给你单链表的头结点 head ,请你找出并返回链表的中间结点。
如果有两个中间结点,则返回第二个中间结点。
2.题解思路
👻方法1:快慢指针(🚀)
思路分析:基于快慢指针思路(两个指针同时出发,慢指针走1步、快指针走两步,当快指针走到链表末尾时此时慢指针指向中点位置)
- 当链表元素个数为奇数,此时slow指向中间节点
- 当链表元素个数为偶数,此时slow指向的是第2个中间节点
- 扩展:如果希望slow指向第1个中间节点,则只需要构建dummy补一个虚拟头节点即可
/** * 🟢 876 链表的中间节点 - https://leetcode.cn/problems/middle-of-the-linked-list/description/ */ public class Solution1 { /** * 思路:快慢指针(两个指针同时出发,慢指针走1步、快指针走两步,当快指针走到链表末尾时此时慢指针指向中点位置) */ public ListNode middleNode1(ListNode head) { ListNode slow = head, fast = head; while (fast != null && fast.next != null) { slow = slow.next; // 慢指针走1步 fast = fast.next.next; // 快指针走2步 } // 在无环情况下fast走到链表尾部,此时slow为中点位置 return slow; // 链表节点个数为奇数slow指向中间结点,链表个数为偶数slow指向第2个中间结点 } public ListNode middleNode(ListNode head) { ListNode dummy = new ListNode(-1, head); ListNode slow = dummy, fast = dummy; while (fast != null && fast.next != null) { slow = slow.next; // 慢指针走1步 fast = fast.next.next; // 快指针走2步 } // 在无环情况下fast走到链表尾部,此时slow为中点位置 return slow; // 链表节点个数为奇数slow指向中间结点,链表个数为偶数slow指向第1个中间结点 } }复杂度分析
时间复杂度:O(n)n 为链表节点个数(链表长度)
空间复杂度:O(1)构建双指针进行遍历(占用常数级空间)
👻方法2:集合处理
- 思路分析:遍历链表元素,然后将其载入集合(数组或者列表均可),通过下标索引快速返回中间节点即可
/**
* 🟢 876 链表的中间节点 - https://leetcode.cn/problems/middle-of-the-linked-list/description/
*/
public class Solution2 {
/**
* 思路:集合处理
*/
public ListNode middleNode(ListNode head) {
List<ListNode> list = new ArrayList<>();
ListNode cur = head;
while (cur != null) {
list.add(cur);
cur = cur.next;
}
// 返回中间节点
return list.get(list.size() / 2);
}
}
复杂度分析
时间复杂度:O(n)n 为链表节点个数(链表长度)
空间复杂度:O(n)构建集合存储元素
👻方法3:单指针(可以理解为集合处理的空间优化版本)
- 思路分析:遍历链表元素,获取到链表的长度,随后再次遍历链表得到中间结点(对比【方法2】的集合处理方式,此处不需要构建辅助集合存储链表),只需要遍历2次链表(第1次获取链表长度,第2次根据链表长度定位中间节点位置)
/**
* 🟢 876 链表的中间节点 - https://leetcode.cn/problems/middle-of-the-linked-list/description/
*/
public class Solution3 {
/**
* 思路:单指针
*/
public ListNode middleNode(ListNode head) {
// ① 第1次遍历:获取链表长度n
int n = 0;
ListNode cur = head;
while (cur != null) {
n++;
cur = cur.next;
}
// ② 第2次遍历:根据链表长度获取中间节点
int midIdx = n / 2;
ListNode pt = head;
while (midIdx-- > 0) {
pt = pt.next;
}
return pt;
}
}
复杂度分析
时间复杂度:O(n)n 为链表节点个数(链表长度)此处需要遍历两次链表(1.5次,第1次获取长度,第2次遍历一半)
空间复杂度:O(1)构建单指针进行遍历(占用常数级空间)
🟡143-重排链表
1.题目内容
给定一个单链表 L 的头节点 head ,单链表 L 表示为:
L0 → L1 → … → Ln - 1 → Ln
请将其重新排列后变为:
L0 → Ln → L1 → Ln - 1 → L2 → Ln - 2 → …
不能只是单纯的改变节点内部的值,而是需要实际的进行节点交换
2.题解思路
👻方法1:顺序遍历 + 重排 (线性表 + 重排链表)
- 思路分析:由于链表并不支持随机访问,因此可以通过顺序遍历的方式将链表节点载入集合中,随后重新根据索引构建新链表
/**
* 🟡 143 重排链表 - https://leetcode.cn/problems/reorder-list/description/
*/
public class Solution1 {
/**
* 思路:遍历链表,装载所有链表节点,然后按照奇偶数位来拼接链表
*/
public void reorderList(ListNode head) {
List<ListNode> list = new ArrayList<>();
ListNode cur = head;
while (cur != null) {
list.add(cur);
cur = cur.next;
}
// 根据奇偶处理新链表
ListNode dummy = new ListNode(-1);
ListNode pt = dummy;
int evenIdx = 0, oddIdx = list.size() - 1;
for (int i = 0; i < list.size(); i++) {
if (i % 2 == 0) {
pt.next = list.get(evenIdx);
pt = pt.next;
evenIdx++;
} else if (i % 2 == 1) {
pt.next = list.get(oddIdx);
pt = pt.next;
oddIdx--;
}
}
pt.next = null; // handle cycle
}
}
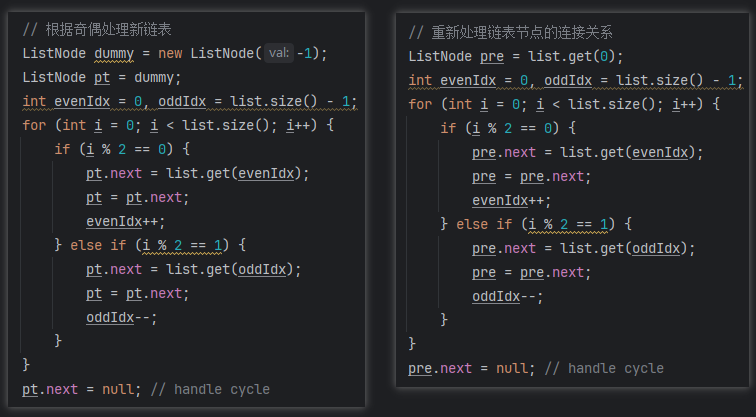
结合代码分析,此处可以构建辅助dummy来处理节点的连接关系(构建新链表,节点引用处理)。也可以直接在原head直接进行处理,此处基于dummy操作也是对节点引用进行处理(实际就是重新构建每个链表节点的连接关系,每次构建完成需要记录pre节点,用于根据索引位置连接pre.next)
复杂度分析
时间复杂度:O(N),其中 N 是链表中的节点数
空间复杂度:O(N),其中 N 是链表中的节点数(主要是线性表的开销)
👻方法2:找中点 + 链表逆序 + 合并链表(🚀)
- 思路分析:该思路综合了链表的基本操作:快慢指针找中点 + 链表原地逆序 + 合并链表 这三种基本操作
- ① 寻找中点:可以基于【快慢指针】寻找链表中点,将链表拆为前后两部分(
left、right) - ② 后半段逆序:将链表的后半段进行原地逆序
- ③ 合并链表:构建
dummy,将两段链表直接进行合并
- ① 寻找中点:可以基于【快慢指针】寻找链表中点,将链表拆为前后两部分(
- 【案例分析1】:
{1,2,3,4,5}- ① 寻找中点:中间节点为
3,将链表拆分为两部分(left:{1,2,3}、right:{4,5}) - ② 后半段逆序:
reverseRight:{5,4} - ③ 合并链表:构建
dummy,将两段链表直接进行合并{1,5,2,4,3}
- ① 寻找中点:中间节点为
- 【案例分析2】:
{1,2,3,4}- ① 寻找中点:中间节点为
3(此处处理如果是偶数个元素则返回的是第2个中间节点),将链表拆分为两部分(left:{1,2,3}、right:{4,5}) - ② 后半段逆序:
reverseRight:{5,4} - ③ 合并链表:构建
dummy,将两段链表直接进行合并{1,5,2,4,3}
- ① 寻找中点:中间节点为
/**
* 🟡 143 重排链表 - https://leetcode.cn/problems/reorder-list/description/
*/
public class Solution3 {
/**
* 思路:寻找中点 + 后半段逆序 + 合并链表
*/
public void reorderList(ListNode head) {
// ① 寻找链表中点并切割链表为两部分(left,right)
ListNode midNode = findMidNode(head);
ListNode right = midNode.next;
midNode.next = null;
ListNode left = head;
// ② 将后半段链表进行逆序
ListNode reverseRight = reverseList(right);
// ③ 合并left、reverseRight
ListNode merge = mergeList(left, reverseRight);
// 返回结果
// return merge;
head = merge;
}
// 寻找链表中点
public ListNode findMidNode(ListNode head) {
// 定义快慢指针寻找链表中点
ListNode slow = head, fast = head;
while (fast != null && fast.next != null) {
slow = slow.next;
fast = fast.next.next;
}
return slow;
}
// 原地反转链表
public ListNode reverseList(ListNode head) {
ListNode pre = null;
ListNode cur = head;
while (cur != null) {
// 记录cur.next
ListNode nxt = cur.next;
// 反转指针
cur.next = pre;
// 滚动更新指针
pre = cur;
cur = nxt;
}
// 返回反转后的链表
return pre;
}
// 合并两个链表
public ListNode mergeList(ListNode l1, ListNode l2) {
ListNode dummy = new ListNode(-1);
ListNode cur = dummy;
// 定义指针遍历两个链表
ListNode p1 = l1;
ListNode p2 = l2;
while (p1 != null && p2 != null) {
// 载入l1链表元素
cur.next = p1;
cur = cur.next;
p1 = p1.next;
// 载入l2链表元素
cur.next = p2;
cur = cur.next;
p2 = p2.next;
}
if (p1 != null) {
cur.next = p1;
}
if (p2 != null) {
cur.next = p2;
}
// 返回合并后的链表
return dummy.next;
}
}
复杂度分析
- 时间复杂度:
- 空间复杂度:
🟢083-删除排序链表中的重复元素(保留1个重复元素)
1.题目内容
给定一个已排序的链表的头 head , 删除所有重复的元素,使每个元素只出现一次 。返回 已排序的链表
例如[1,1,2] => [1,2] ; [1,1,2,3,3] => [1,2,3] (只保留一个重复元素)
2.题解思路
👻方法1:一次遍历
对比203-移除链表元素,可以看到此处是要保留一个重复的元素,可以理解为当这个重复元素出现在头结点的时候也是要保留一个的,因此此处不用引入dummy虚拟头节点来辅助(dummy是用来辅助处理头节点问题的),而是直接用head进行遍历处理
- 思路分析:由于链表本身有序,因此可以通过一次遍历,在遍历过程中校验相邻的两个数是否相同,如果相同则执行删除操作即可
- 例如遍历到
cur,则校验cur.val == cur.next.val是否成立,如果成立则执行删除操作(保留cur,删除cur.next)
- 例如遍历到
/**
* 🟢 083 删除排序链表中的重复元素 - https://leetcode.cn/problems/remove-duplicates-from-sorted-list/description/
*/
public class Solution1 {
/**
* 思路分析:一次遍历,基于已排序的链表,删除连续出现的元素
*/
public ListNode deleteDuplicates(ListNode head) {
if (head == null) {
return null;
}
// 构建虚拟头节点
ListNode cur = head;
// 此处链表本身有序,校验cur和cur.next是否连续重复,如果出现连续重复则删除cur.next
while (cur.next != null) {
if (cur.val == cur.next.val) {
cur.next = cur.next.next; // 删除cur.next,则cur指向的是当前待删除节点的前一个节点,修改其next指针
} else {
cur = cur.next; // 指针后移,遍历下一个元素
}
}
return head;
}
}
复杂度分析
时间复杂度:O(N) n 为链表节点个数
空间复杂度:O(1)占用常数级空间辅助删除操作
🟡082-删除排序链表中的重复元素(不保留重复元素)
1.题目内容
给定一个已排序的链表的头 head , 删除原始链表中所有重复数字的节点,只留下不同的数字 。返回 已排序的链表
例如[1,2,3,3,4,4,5] => [1,2,5] ; [1,1,1,2,3] => [2,3] (不保留重复元素)
2.题解思路
👻方法1:模拟法
- 思路分析:此处删除排序链表中的重复元素并且不保留这个重复元素,可以基于模拟的思路,先找到链表中的所有重复元素,然后依次执行删除操作
- ① 记录每个元素出现的次数(
Map<元素,出现次数>) - ② 校验元素出现次数,如果出现超出1次则执行相应次数的删除操作(不保留重复元素)(调用
deleteNode()方法删除指定目标值)
- ① 记录每个元素出现的次数(
复杂度分析
时间复杂度:
空间复杂度:
👻方法2:一次遍历
- 思路分析:一次遍历,遍历的过程校验连续重复的值并删除
/**
* 🟡 082 删除排序链表中的重复元素II - https://leetcode.cn/problems/remove-duplicates-from-sorted-list-ii/description/
*/
public class Solution1 {
/**
* 思路:一次遍历
*/
public ListNode deleteDuplicates(ListNode head) {
// 构建虚拟头节点
ListNode dummy = new ListNode(-1, head);
ListNode cur = dummy; // cur 初始化指向虚拟头节点
// 对链表进行遍历
while (cur.next != null && cur.next.next != null) {
int val = cur.next.val; // 记录元素
if (cur.next.next.val == val) { // 如果出现重复,则不断校验并删除这个重复的元素
while (cur.next != null && cur.next.val == val) {
cur.next = cur.next.next;
}
} else {
// 当cur.next 元素 不等于 cur.next.next 此时说明链表中只有一个值为cur.next的节点,因此此时可以将cur指向cur.next
cur = cur.next;
}
}
// 链表遍历完成,返回哑节点的下一个节点
return dummy.next;
}
}
复杂度分析
时间复杂度:
空间复杂度:
🟡148-排序链表
1.题目内容
给你链表的头结点 head ,请将其按 升序 排列并返回 排序后的链表 。
例如:[4->2->1->3] => [1->2->3->4]、[(-1)->5->3->4->0] => [(-1)->0->3->4->5]
2.题解思路
👻方法1:模拟法
- 思路分析:模拟法又称暴力法,以解决题目为目的,按照模拟思路一步步处理得到解决方案。此处的思路就是借助list存储链表元素,然后再对list进行排序,基于排序后的list构建新链表并返回
/**
* 🟡 148 排序链表 - https://leetcode.cn/problems/sort-list/description/
*/
public class Solution148_01 {
/**
* 思路分析:借助辅助集合进行排序
*/
public ListNode sortList(ListNode head) {
List<Integer> list = new ArrayList<>();
ListNode cur = head;
while (cur != null) {
list.add(cur.val);
cur = cur.next;
}
// 对集合元素进行排序
Collections.sort(list);
// 基于排序后的元素序列构建新链表
ListNode dummy = new ListNode(-1);
ListNode pt = dummy;
for (int i = 0; i < list.size(); i++) {
pt.next = new ListNode(list.get(i));
pt = pt.next;
}
pt.next = null; // handle cycle
// 返回构建的链表
return dummy.next;
}
}
复杂度分析
时间复杂度:需遍历两遍数组 + 排序的时间消耗(第1次遍历获取链表元素序列,随后执行排序,第2次遍历则填充新链表)
空间复杂度:需要借助集合辅助遍历,集合占用空间取决于链表长度
👻方法2:
- 思路分析:基于【思路1】的设计可以进一步思考如何进行优化,此处的核心在于优化排序,因此可以考虑基于归并排序的思路来完成排序
- ① 找中点:找到链表中点,以中点为界,将链表拆分为两个子链表
- 此处寻找链表中点选择的应该是"借助dummy构建"(返回中间节点的第1个节点),处理递归过程中的异常问题(如果返回的是第2个中间节点则会导致栈溢出问题)
- ② 分:对子链表分别进行排序
- ③ 合:将排序后的子列表进行合并(此处可以使用【合并两个有序链表】的思路去做:直接遍历合并或者借助堆来进行合并)
- ① 找中点:找到链表中点,以中点为界,将链表拆分为两个子链表
/**
* 🟡 148-单链表排序 - https://leetcode.cn/problems/sort-list/
*/
public class Solution3 {
/**
* 归并排序思路:
* ① 找中点、拆分两个链表
* ② 分:分别对两个链表进行排序
* ③ 合:将排序后的两个链表进行合并(参考【合并两个有序链表思路】)
*/
public ListNode sortList(ListNode head) {
if (head == null || head.next == null) {
return head;
}
// 寻找链表中点
ListNode midNode = findMid(head);
// 拆分链表,并对拆分的链表分别进行排序
ListNode right = sortList(midNode.next);
midNode.next = null;
ListNode left = sortList(head);
// 合并排序后的链表
ListNode mergeNode = merge(left, right);
return mergeNode;
}
// 寻找链表中点(快慢指针思路)
private ListNode findMid(ListNode head) {
ListNode dummy = new ListNode(-1, head);
// 定义快慢指针寻找中点(此处返回的是第1个节点)
ListNode slow = dummy, fast = dummy;
while (fast != null && fast.next != null) {
slow = slow.next;
fast = fast.next.next;
}
// 返回中点
return slow;
}
// 合并两个有序链表(双指针)
private ListNode merge(ListNode l1, ListNode l2) {
// 构建虚拟头节点
ListNode dummy = new ListNode(-1);
ListNode cur = dummy;
// 定义指针分别遍历两个链表
ListNode p1 = l1;
ListNode p2 = l2;
while (p1 != null && p2 != null) {
// 选择较小的值载入
if (p1.val <= p2.val) {
cur.next = p1;
cur = cur.next;
p1 = p1.next;
} else {
cur.next = p2;
cur = cur.next;
p2 = p2.next;
}
}
// 处理尾巴
if (p1 != null) {
cur.next = p1;
}
if (p2 != null) {
cur.next = p2;
}
// 返回构建的新链表
return dummy.next;
}
}
复杂度分析
时间复杂度:
空间复杂度:
此处符合处理的findMid写法
// 寻找链表中点(快慢指针思路)
private ListNode findMid(ListNode head) {
// 定义快慢指针寻找中点
ListNode slow = head, fast = head.next;
while (fast != null && fast.next != null) {
slow = slow.next;
fast = fast.next.next;
}
// 返回中点
return slow;
}
// 寻找链表中点(快慢指针思路)
private ListNode findMid(ListNode head) {
ListNode dummy = new ListNode(-1, head);
// 定义快慢指针寻找中点(此处返回的是第1个节点)
ListNode slow = dummy, fast = dummy;
while (fast != null && fast.next != null) {
slow = slow.next;
fast = fast.next.next;
}
// 返回中点
return slow;
}
// 寻找链表中点(快慢指针思路)
private ListNode findMid(ListNode head) {
// 定义快慢指针寻找中点
ListNode slow = head, fast = head.next;
while (fast.next != null && fast.next.next != null) {
slow = slow.next;
fast = fast.next.next;
}
// 返回中点
return slow;
}
123-回文链表
1.题目内容
2.题解思路
👻方法1:
复杂度分析
时间复杂度:
空间复杂度:
