skill-01-数组
难度说明:🟢简单🟡中等🔴困难
学习资料
学习目标
- 掌握数据结构核心基础
- 借助数据结构完成常见题型
skill-01-数组
理论基础
1.核心理论
- 【数组】
- 数组的下标是从0开始的
- 数组的内存空间地址是连续的(因此在增删元素的时候不可避免需要移动其他元素的地址)
2.技巧总结
- 数据检索场景中:时间复杂度O(logN)可以说是二分法的代名词
🍚二分查找技巧
二分查找通用规律
/**
* 范围查询规律
* 初始化:
* int left = 0;
* int right = nums.length - 1;
* 循环条件
* left <= right
* 右边取值
* right = mid - 1
* 左边取值
* left = mid + 1
* 查询条件
* >= target值, 则 nums[mid] >= target时, 都减right = mid - 1
* > target值, 则 nums[mid] > target时, 都减right = mid - 1
* <= target值, 则 nums[mid] <= target时, 都加left = mid + 1
* < target值, 则 nums[mid] < target时, 都加left = mid + 1
* 结果
* 求大于(含等于), 返回left
* 求小于(含等于), 返回right
* 核心思想: 要找某个值, 则查找时遇到该值时, 当前指针(例如right指针)要错过它, 让另外一个指针(left指针)跨过他(体现在left <= right中的=号), 则找到了
*/
二分查找区间技巧
在二分法检索问题中,对于有序数组和target,需要注意几方面的内容(需注意数组元素的有序性和重复性)
① 数组必须有序:须确保使用二分法之前数组元素必须有序,否则范围缩减没有意义
② 数组元素是否重复:如果数组中不存在重复元素,那么查找目标target是唯一的,但是如果数组存在重复元素,则查找到的target索引位置可能并不唯一
二分查找技巧核心(理解不同区间定义的实现方案)
(1)数据溢出问题
中点取值int mid = (left + right)/2存在数据溢出问题,因此调整为int mid = left + (right - left)/2(先减后加,避免相加后数据太大导致数据溢出问题)
(2)循环退出条件
当查找区间为空的时候循环结束(因此要确定优先的区间选择的有效的取值范围)循环不变量
(3)区间取值问题(不同区间取值的处理)
二分法需注意,区间的定义在于区间内的数(下标)都是还没确定与target的大小关系的,区间外的数是确定了与target的大小关系
二分查找的循环不变量
循环不变量是指在循环过程中始终保持成立的条件。 对于二分查找来说,循环不变量通常是这样的: 在每次循环开始前,查找范围始终包含待查找元素。 在每次循环过程中,查找范围不断缩小,直到找到目标元素或者确认目标元素不存在
在二分查找的过程中,保持不变量,就是在while寻找中每一次边界的处理都要坚持根据区间的定义来操作,让循环内的区间始终满足定义的性质,这就是循环不变量规则
(1)二分查找模板(不同区间处理)
对于不同的查找模板需要注意下述几点
- 初始区间取值(
[left,right]、(left,right]、(left,right))- 闭区间:
[0,len-1] - 左闭右开:
[0,len) - 开区间:
(-1,len)
- 闭区间:
- 循环退出条件(取决于区间的定义,可以从区间取值来理解)循环不变量,基于区间限定
- 闭区间:
while(left<=right)取的是闭区间,left是可以取到right位置的(例如right最大为len-1),即理解left==right时,[left,right]的取值是有效的 - 左闭右开:
while(left<right)取得是左闭右开区间,left不可以取到right位置的,即理解left==right时,[left,right)的取值是无效的,进而说明left不能取等于right - 开区间:
while(left+1<right)取得是闭区间,此处判断的应该是left+1,且left+1不可以取到right位置
- 闭区间:
- 区间选择(闭区间、左闭右开、开区间):二分法区间内都是还没确定与target的大小关系的,区间外的数是确定了与target的大小关系
(1)闭区间([left,right])
// 闭区间
public int binarySearch1(int[] nums, int target) {
// 定义检索区间
int left = 0, right = nums.length - 1; // 闭区间
while (left <= right) {
int mid = left + (right - left) / 2;
if (target < nums[mid]) {
// 如果目标在左侧,则右侧缩边
right = mid - 1;
} else if (target > nums[mid]) {
// 如果目标在右侧,则左侧缩边
left = mid + 1;
} else {
return mid;
}
}
// 返回元素可插入的下个位置(如果不存在可以直接返回-1)
return left; // return -1;
}
public int binarySearch1(int[] nums, int target) {
// 定义检索区间
int left = 0, right = nums.length - 1; // 闭区间
while (left <= right) { // 区间不为空时
int mid = left + (right - left) / 2;
if (nums[mid]<target) {
left = mid + 1; // 取[mid+1,right]区间
} else{
right = mid -1; // 取[left,mid-1]区间 (target==nums[mid]的情况也包括在内)
}
}
// 返回元素可插入的下个位置(如果不存在可以直接返回-1)
return left; // return -1;
}
(2)左闭右开([left,right))
// 左闭右开区间
public int binarySearch2(int[] nums, int target) {
// 定义检索区间
int left = 0, right = nums.length; // 闭区间
while (left < right) { // 区间不为空时
int mid = left + (right - left) / 2;
if (nums[mid]<target) {
left = mid + 1; // 取[mid+1,right)区间
} else{
right = mid ; // 取[left,mid)区间 (target==nums[mid]的情况也包括在内)
}
}
// 返回查找到的target所在索引
return left; // return right;
}
(3)开区间((left,right))
// 左闭右开区间
public int binarySearch3(int[] nums, int target) {
// 定义检索区间
int left = -1, right = nums.length; // 开区间(左开右开)
while (left + 1 < right) { // 区间不为空时
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid; // 取(mid,right)区间
} else {
right = mid; // 取(left,mid)区间 (target==nums[mid]的情况也包括在内)
}
}
// 返回查找到的target所在索引
return right;
}
常见题型
🟢704-二分查找
1.题目内容
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1
2.题解思路
题解思路分析
- 【1】遍历法:普通遍历,检索target
- 【2】二分法:充分利用有序数组的特性,借助二分法完成
👻方法1:二分法
- 思路分析:充分利用有序数组的特性,借助二分法完成(闭区间、左闭右开区间、开区间 三种思路,思路大同小异,但需注意一些区间选择的细节)
- 初始区间设定
- 遍历循环条件设定
mid指针获取(防止溢出)- 区间选择(根据target在哪个区间进行缩边,需注意区间开闭问题)
/**
* 704 二分查找
*/
public class Solution1 {
/**
* 二分法思路(开区间)
*/
public int search(int[] nums, int target) {
// 初始化左右指针
int left = -1, right = nums.length; // todo 开区间
// 遍历
while (left + 1 < right) { // todo 开区间循环条件限制 (left从-1开始计数,此处要确保区间有效)
// 获取mid指针
int mid = left + (right - left) / 2;// 防止溢出(等价于(left+right)/2)
if (nums[mid] < target) {
// target在右侧区间,左侧缩边
left = mid; // todo 开区间(区间更新:(mid,right))
} else if (nums[mid] == target) {
// 目标值存在,返回下标
return mid;
} else if (nums[mid] > target) {
// target在左侧区间,右侧缩边
right = mid; // todo 开区间(区间更新:(left,mid))
}
}
// 元素不存在返回-1
return -1;
}
/**
* 二分法思路(左闭右开区间)[left,right)
*/
public int search2(int[] nums, int target) {
// 初始化左右指针
int left = 0, right = nums.length; // todo 左闭右开 (区间取值:[left,right))
// 遍历
while (left < right) { // todo 左闭右开循环条件限制(当left==right的情况下,此时[left,right) 会变成一个无效空间,因此此处取<小于)
// 获取mid指针
int mid = left + (right - left) / 2;// 防止溢出(等价于(left+right)/2)
if (nums[mid] < target) {
// target在右侧区间,左侧缩边
left = mid + 1; // todo 左闭右开 (区间更新:[mid+1,right))
} else if (nums[mid] == target) {
// 目标值存在,返回下标
return mid;
} else if (nums[mid] > target) {
// target在左侧区间,右侧缩边
right = mid; // todo 左闭右开 (区间更新:[left,mid))
}
}
// 元素不存在返回-1
return -1;
}
/**
* 二分法思路(闭区间)[left,right]
*/
public int search1(int[] nums, int target) {
// 初始化左右指针
int left = 0, right = nums.length - 1; // todo 闭区间
// 遍历
while (left <= right) { // todo 闭区间循环条件限制
// 获取mid指针
int mid = left + (right - left) / 2; // 防止溢出(等价于(left+right)/2)
if (nums[mid] < target) {
// target在右侧区间,左侧缩边
left = mid + 1; // todo 闭区间(区间更新:[mid+1,right])
} else if (nums[mid] == target) {
// 目标值存在,返回下标
return mid;
} else if (nums[mid] > target) {
// target在左侧区间,右侧缩边
right = mid - 1; // todo 闭区间(区间更新:[left,mid-1])
}
}
// 元素不存在返回-1
return -1;
}
}
复杂度分析
时间复杂度:O(logN)N 数组长度
空间复杂度:O(1)
🟢027-移除元素
1.题目内容
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素。元素的顺序可能发生改变。然后返回 nums 中与 val 不同的元素的数量。
假设 nums 中不等于 val 的元素数量为 k,要通过此题,您需要执行以下操作:
- 更改
nums数组,使nums的前k个元素包含不等于val的元素。nums的其余元素和nums的大小并不重要 - 返回
k
2.题解思路
思路分析
- 【1】硬核遍历❌(非原地算法):中规中矩通过遍历的方式找到所有非target元素,然后组装成新数组
- 【2】覆盖法(快慢指针思路)🟢(原地算法):通过定义快慢指针依次完成非target值的数组覆盖(用非target依次覆盖数组,两个指针同向)
👻方法1:覆盖法(快慢指针思路)
思路分析:覆盖法(快慢指针思路):将非val数据依次按顺序覆盖数组
参考【移动零】的例子,也是类似的将目标值移动到数组尾部,实际上就是将非target依次覆盖数组
所谓快慢指针概念:
- 慢指针:指向更新 即待更新的数组下标位置
- 快指针:寻找目标元素(非target),然后将该元素覆盖到慢指针指向位置,随后两指针继续后移

/**
* 027 移除元素
*/
public class Solution1 {
// 覆盖法(参考移动0的思路):将非val数据依次按顺序覆盖数组
public int removeElement(int[] nums, int val) {
int idx = 0; // idx 指向当前要覆盖的元素位置
for (int i = 0; i < nums.length; i++) {
// 如果遍历指向元素为非val,则将其移动到前面(覆盖(由于题意不care其他的内容,因此可以直接覆盖))
if (nums[i] != val) {
nums[idx] = nums[i]; // 直接覆盖(或者自定义方法进行交换)
idx++; // idx 指向下一个覆盖的位置
}
}
return idx;
}
}
复杂度分析
时间复杂度:O(n)n 为数组长度
空间复杂度:O(1)
👻方法2:双指针思路
- 思路分析:双指针思路(左:指向存储val的位置,右:指向存储非val的位置,两者在指定条件下需进行交换)
- 左右指针:左指针找val位置,右指针找非val位置,找到了两者就进行交换
- 易错点:为了避免思路混淆,单次循环尽量只移动一个指针位置(避免指针越界)
/**
* 027 移除元素
*/
public class Solution2 {
// 双指针
public int removeElement(int[] nums, int val) {
// 初始化左右指针
int left = 0, right = nums.length - 1;
// 指针相遇遍历结束
while (left <= right) {
// 判断当前的左右指针的位置
if (nums[left] == val) {
// 如果左侧找到了存储val的位置,则需进一步确定右侧的位置
if (nums[right] != val) {
// 满足条件,进行交换
int temp = nums[left];
nums[left] = nums[right];
nums[right] = temp;
} else {
right--; // 该位置不满足,right继续往前
}
} else {
// 左侧位置不满足,left继续往前
left++;
}
}
// 返回结果
return left;
}
}
复杂度分析
时间复杂度:O(n)
空间复杂度:O(1)
🟢977-有序数组的平方
1.题目内容
给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。
示例 1:
输入:nums = [-4,-1,0,3,10]
输出:[0,1,9,16,100]
解释:平方后,数组变为 [16,1,0,9,100]
排序后,数组变为 [0,1,9,16,100]
示例 2:
输入:nums = [-7,-3,2,3,11]
输出:[4,9,9,49,121]
2.题解思路
思路分析
- 【1】硬核方式:计算平方+直接排序
- 【2】双指针:首尾比较(计算平方)+逆序存放
👻方法1:计算平方+直接排序
- 思路分析
// 计算平方 + 直接排序
public int[] sortedSquares(int[] nums) {
// 1.计算平方
for(int i=0;i<nums.length;i++){
nums[i] *= nums[i];
}
// 2.直接排序
Arrays.sort(nums);
return nums;
}
复杂度分析
时间复杂度:O(nlogn),其中 n 是数组 nums 的长度
空间复杂度:O(logn)。除了存储答案的数组以外,需要 O(logn) 的栈空间进行排序
👻方法2:双指针(计算平方+逆序存放)
- 思路分析:定义双指针从头尾相向遍历,选择平方数较大(绝对值较大的元素)的依次从新数组的尾部开始逆序存放(不要局限于原地数组操作,可以借助辅助数组来实现)
- 因为数组元素可能为负数,如果是求平方后排序的话,原来的负数求的平方后可能会变大,基于此可以采用双指针的思路,分别从头尾向中间靠拢,依次进行比较,将平方数较大的值依次从新数组的尾部逆序存放
// 计算平方 + 逆序存放
public int[] sortedSquares(int[] nums) {
int len = nums.length;
// 定义数组存放数组元素
int[] newNums = new int[len];
int idx = len - 1; // idx 存放指定下标元素
// 定义头尾指针
int start = 0, end = len - 1;
// 原数组本身有序,因此需比较平方和大小,然后将较大的元素从newNums队尾开始遍历
for (int i = 0; i < nums.length; i++) {
if (Math.abs(nums[start]) >= Math.abs(nums[end])) {
newNums[idx] = nums[start] * nums[start];
start++;
idx--; // 逆序存放,指针前移
} else {
newNums[idx] = nums[end] * nums[end];
end--;
idx--; // 逆序存放,指针前移
}
}
// 返回构建的数组
return newNums;
}
复杂度分析
时间复杂度:O(n)需要遍历整个数组
空间复杂度:O(n)需要一个存储结果的数组以及额外的常数级空间
类似写法
/**
* 🟢 977 有序数组的平方 - https://leetcode.cn/problems/squares-of-a-sorted-array/description/
*/
public class Solution977_02 {
/**
* 思路分析:数组本身按照非递减顺序排序,返回每个数字的平方组成的新数组
* 双指针思路,定义两端指针进行相向遍历,绝对值较大的元素其平方和也较大,将绝对值较大的元素从后往前进行平方和填充
* O(n)时间复杂度(需遍历整个数组),O(n)空间复杂度(需借助辅助集合存储结果集)
*/
public int[] sortedSquares(int[] nums) {
int n = nums.length;
// 定义平方和结果集
int[] res = new int[n];
int left = 0, right = n - 1; // 定义双指针相向遍历,选择绝对值较大的元素进行填充(从后往前)
int cur = n - 1; // 定义指针从后往前遍历填充平方和
while (left <= right) {
// 校验平方和
if (Math.abs(nums[left]) > Math.abs(nums[right])) { // left 指向元素绝对值较大,优先选择填充
res[cur] = nums[left] * nums[left];
cur--;
left++;
} else {
res[cur] = nums[right] * nums[right]; // right 指向元素绝对值较大,优先选择填充
cur--;
right--;
}
}
// 返回结果集
return res;
}
}
🟡209-长度最小的子数组
1.题目内容
给定一个含有 n 个正整数的数组和一个正整数 target **。**找出该数组中满足其总和大于等于 target 的长度最小的 子数组
[numsl, numsl+1, ..., numsr-1, numsr] ,并返回其长度**。**如果不存在符合条件的子数组,返回 0 。
注意:子数组要确保在原来数组的连续性(任何一个子数组摘出来能在原数组找到连续片段),不能进行排序
2.题解思路
👻方法1:滑动窗口
思路分析:定义滑动窗口,存储满足条件的元素,在窗口滑动的过程中计算元素总和
初始化:left、right 从起点0开始
右侧纳新+左侧缩边:当窗口没有滑动到右侧的时候,不断纳新(加入新的元素),然后判断当前的curSum(窗口内元素之和)是否满足大于等于target,如果满足则需要记录满足条件的数组的长度并更新min,记录完成需要逐步将左侧的元素移出(直到curSum<target)以接收新的元素,整个过程都需要记录min的变化(需注意right指针的变化放在最后,避免对索引计算造成影响)
- 大白话:数组所有元素都为正数,每一次遍历右指针不断加入新元素,如果发现
cur>=target则在此基础上记录min并且左指针缩边不断移出元素才有可能在下次遍历的时候让新元素加入进来 - 移动窗口:(right 边界移动到数组末尾则结束,left 边界的控制则交由每次遍历控制)
- ① 加入新元素
nums[right] - ② 校验curSum与target的值,如果满足大于等于则不断移出left指向元素并记录minLen
- ③ 当次处理结束right指针移动指向下一个元素(right的变更放在最后是因为步骤②中会用到right)
- ① 加入新元素

- 大白话:数组所有元素都为正数,每一次遍历右指针不断加入新元素,如果发现
/**
* 🟡 209 长度最小的子数组 - https://leetcode.cn/problems/minimum-size-subarray-sum/
* 求满足数组中其总和大于等于target的长度最小的子数组
*/
public class Solution209_01 {
/**
* 思路分析:滑动窗口思路
* 定义一个窗口,窗口中限定刷入满足总和大于等于target的元素,left用于剔除,right用于纳新,计算满足条件的窗口(子数组)长度min
*/
public int minSubArrayLen(int target, int[] nums) {
int minSubLen = Integer.MAX_VALUE; // 定义初始值
int n = nums.length;
// 定义滑动窗口的左右边界指针
int left = 0, right = 0;
// 定义窗口内元素和(随着窗口的滑动变更)
int curSum = 0;
while (right < n) {
// ① 尝试加入新元素
curSum += nums[right];
// ② 如果curSum>=target,说明此时窗口内满足要求,记录minSubLen,并通过不断剔除左侧元素进行校验(左边界缩圈,为接收下一个可能的新元素做准备,直到curSum<target)
while (curSum >= target) {
minSubLen = Math.min(minSubLen, right - left + 1); // 更新满足条件的子数组的最小长度
// 剔除左侧元素(不断移出左侧元素,直到curSum<target,为加入下一个新元素做准备)
curSum -= nums[left++];
}
// ③ right 移动(指向下一个要纳入的元素)
right++; // right 的变更放在后面(前面步骤②需要用到原来的right计算minSubLen)
}
// 返回结果
return minSubLen == Integer.MAX_VALUE ? 0 : minSubLen; // 如果为初始的MAX说明不存在满足条件的子数组
}
}
复杂度分析
- 时间复杂度:O(n),其中 n 是数组的长度。指针 start 和 end 最多各移动 n 次
- 空间复杂度:O(1) 常数级空间占用
👻方法2:暴力解法(❌超时)
- 思路分析:双层暴力解法(
i敲定起点,j敲定终点),相当于把所有子数组都计算一遍- 起点、终点:
i、j
- 起点、终点:
// 暴力法:i 敲定起点,j敲定终点 (相当于把所有子数组都计算一遍)
public int minSubArrayLen(int target, int[] nums) {
int len = nums.length;
int min = Integer.MAX_VALUE; // 最小值
// 嵌套循环:i 敲定起点,j敲定终点
for (int i = 0; i < len; i++) { // 注意循环条件设定和数组越界问题
int curSum = 0;
for (int j = i; j < len; j++) { // 元素本身也算是一个子数组,此处设定起点相同
// 计算[i,j]的元素之和
curSum += nums[j];
// 判断curSum是否大于等于target
if (curSum >= target) {
min = Math.min(min, j - i + 1);
}
}
}
// 返回满足条件的最小长度
return min == Integer.MAX_VALUE ? 0 : min;
}
复杂度分析
- 时间复杂度:O(n2)
- 空间复杂度:O(1)
🟡059-螺旋矩阵II
1.题目内容
给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
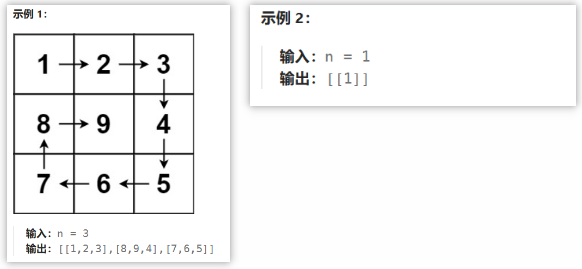
2.题解思路
👻方法1:4指针 + 4方向 遍历
- 思路分析:4指针+4方向 遍历(遍历完1行或1列就缩边)=>从左到右(遍历top行)、从上到下(遍历right列)、从右到左(遍历bottom行)、从下到上(遍历left列)
- 注意点:
- ① 注意某一行或某一列遍历完成才移动指针(指针移动不是放在for内部,而是for结束遍历完一个方向才移动指针/缩边)
- ② 引入count/cur指针用于计数,因此while条件也可控制为
cur<=n*n
- 注意点:
// 思路:4指针+4方向遍历(遍历完1行或1列就缩边)
public int[][] generateMatrix(int n) {
// 定义二维矩阵
int[][] martix = new int[n][n];
// 循环遍历存储元素
int top = 0, bottom = n - 1, left = 0, right = n - 1;
int count = 1;
// 分别从4个方向封装数据
while (top <= bottom && left <= right) { // 注意循环条件:边界重合
// 从左到右(row不变,col变)
for (int i = left; i <= right; i++) {
martix[top][i] = count;
count++;
}
top++; // 单行遍历完成,top下移
// 从上到下(row变,col不变)
for (int i = top; i <= bottom; i++) {
martix[i][right] = count;
count++;
}
right--; // 单列遍历完成,right左移
// 从右到左(row不变,col变)
if (top <= bottom) { // 存在行才需遍历
for (int i = right; i >= left; i--) {
martix[bottom][i] = count;
count++;
}
}
bottom--; // 单行遍历完成,bottom上移
// 从下到上(row变,col不变)
if (left <= right) { // 存在列才需遍历
for (int i = bottom; i >= top; i--) {
martix[i][left] = count;
count++;
}
}
left++; // 单列遍历完成,left右移
}
// 返回最终封装的矩阵
return martix;
}
复杂度分析
时间复杂度:O(n2)需遍历n×n个元素
空间复杂度:O(n2)需矩阵存储遍历元素 + O(1)常数级别的数据
简化版本参考(思路一样,代码简化)
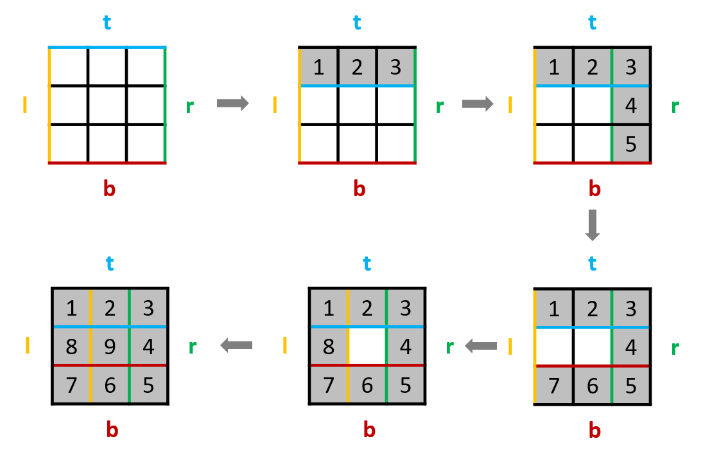
class Solution {
public int[][] generateMatrix(int n) {
int l = 0, r = n - 1, t = 0, b = n - 1;
int[][] mat = new int[n][n];
int num = 1, tar = n * n;
while(num <= tar){
for(int i = l; i <= r; i++) mat[t][i] = num++; // left to right.
t++;
for(int i = t; i <= b; i++) mat[i][r] = num++; // top to bottom.
r--;
for(int i = r; i >= l; i--) mat[b][i] = num++; // right to left.
b--;
for(int i = b; i >= t; i--) mat[i][l] = num++; // bottom to top.
l++;
}
return mat;
}
}
🟢1365-有多少小于当前数字的数字
1.题目内容
给你一个数组 nums,对于其中每个元素 nums[i],请你统计数组中比它小的所有数字的数目。
换而言之,对于每个 nums[i] 你必须计算出有效的 j 的数量,其中 j 满足 j != i 且 nums[j] < nums[i] 。
以数组形式返回答案。
2.题解思路
👻方法1:遍历法(双层循环搜索)
- 思路分析:外层循环确定每一个
nums[i],内层循环遍历数组元素找出比它小的数并统计数量
/**
* 🟢 1365 有多少小于当前数字的数字
*/
public class Solution1 {
// 遍历检索
public int[] smallerNumbersThanCurrent(int[] nums) {
// 定义统计结果数组
int[] res = new int[nums.length];
// 外层确定nums[i]
for (int i = 0; i < nums.length; i++) {
// 内层遍历数组,并统计小于当前元素的元素个数
int cnt = 0;
for (int j = 0; j < nums.length; j++) {
if (nums[j] < nums[i]) {
cnt++;
}
}
// 统计完成,处理结果
res[i] = cnt;
}
// 返回结果
return res;
}
}
复杂度分析
时间复杂度:O(n2)双层循环暴力查找
空间复杂度:O(n)定义
res[]存储结果数组
👻方法2:优化暴力搜索
- 思路分析:基于上述双层循环暴力查找,思考相应的优化思路
- ① 如何找到小于当前数字的数字? =》当数组从小到大进行排序之后,这个数字之前的数字都比它小
- 以
[8,1,2,3,7]为例,对数字进行排序得到[1,2,3,7,8],每个元素比它小的数字统计则取决于前面的元素个数(与当前索引一致),得到[0,1,2,3,4]。但是这个个数需要与原数组的索引下标进行适配,最终得到[4,0,1,2,3]
- 以
- ② 如果出现重复数字怎么处理?例如
[8,1,2,2,3],当出现重复元素,针对重复元素而言情况是一样的。即排序后为[1,2,2,3,8],得到[0,1,1,3,8](也就是说,当遇到不重复的情况索引值即为对应的比它小的数字统计,而对于重复的情况其应该与前面的保持一致(可以用prev记录))
- ① 如何找到小于当前数字的数字? =》当数组从小到大进行排序之后,这个数字之前的数字都比它小
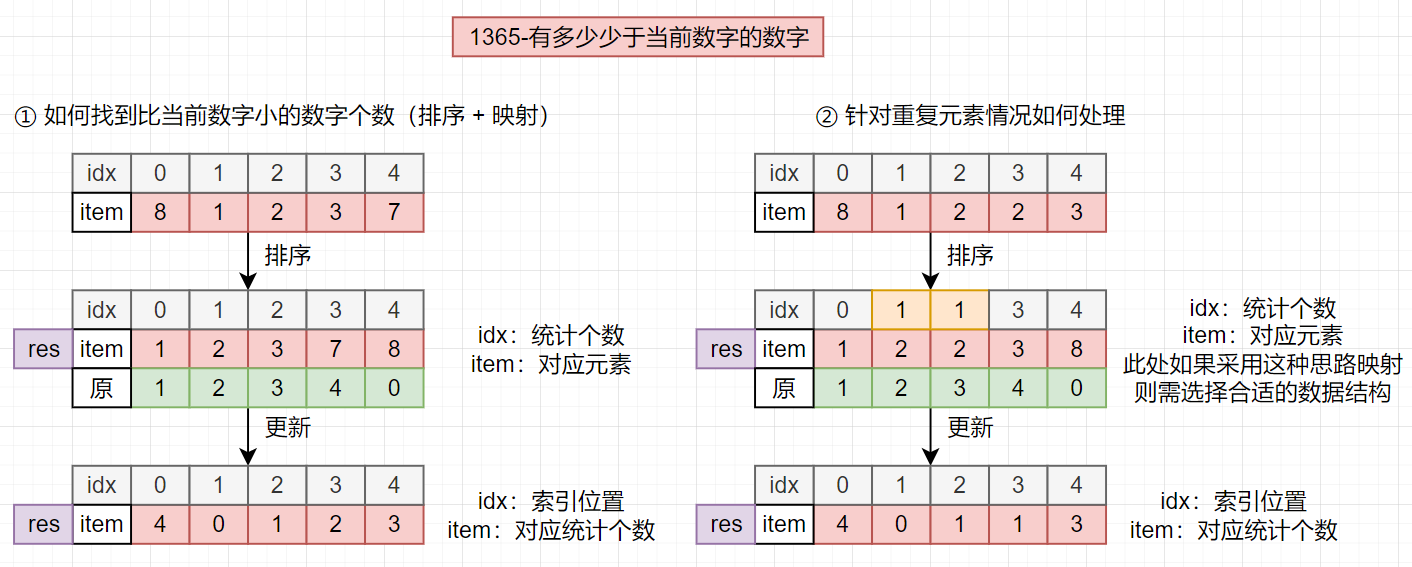
/**
* 🟢 1365 有多少小于当前数字的数字
*/
public class Solution2 {
// 排序法
public int[] smallerNumbersThanCurrent(int[] nums) {
int len = nums.length; // 定义数组长度
int[] res = new int[nums.length]; // 定义统计结果数组
// 对数组元素进行排序,找到第一个小于它的元素(数组元素可能重复,此处不适合用map处理,可以借助二维数组构建数组元素与原有索引坐标的关系)
int[][] numMap = new int[len][2]; // [{ 元素值,对应原有坐标 }]
for (int i = 0; i < len; i++) {
numMap[i][0] = nums[i];
numMap[i][1] = i;
}
// 对二维数组进行排序(从小到大),则此时索引数字对应为前面有多少个比它小的数字
Arrays.sort(numMap, new Comparator<int[]>() {
@Override
public int compare(int[] o1, int[] o2) {
return o1[0] - o2[0]; // 根据元素值大小"从小到大"进行排序
}
});
/**
* 遍历每个元素,找到第1个比它小的元素(因为此处对数组进行了排序,所以当出现不连续的情况则需出现了比它小的数)
* 数组本身有序,如果元素不重复的情况下,则索引值即为比当前元素小的数字个数
* 但是如果元素出现重复,针对重复的情况则需要限定其与前面出现的保持一致
*/
int prev = -1; // 记录第一个出现的数字比它小的数字个数(如果是连续出现则不变)
for (int x = 0; x < numMap.length; x++) {
// 如果初始化状态下或者是出现不连续的情况,则记录这个prev
if (prev == -1 || numMap[x - 1][0] != numMap[x][0]) {
prev = x; // 索引即为相应统计
}
// 处理对应索引位置的结果(根据原来的索引位置封装结果)
res[numMap[x][1]] = prev;
}
// 返回处理结果
return res;
}
}
参考另一种写法思路:
- 定义
res数组(将数组numscopy过来),定义Map存储元素及其比它小的数字个数 - ① 排序:对
res数组进行排序,- 针对非重复元素:
idx即为比当前元素小的数字个数 - 针对重复元素:以重复元素出现的第1个索引位置作为比它小的数字个数
- 针对非重复元素:
- ② 统计:封装
map,遍历res根据上述规律封装元素及其比它小的数字个数。当key重复出现则可以跳过(对于同一元素而言,其【比它小的数字个数】都是一致的) - ③ 更新:再次更新
res,此处res[i]=map.get[nums[i]](要根据对应索引位置上的元素,根据map获取其比它小的数字个数,然后更新res[])
/**
* 🟢 1365 有多少小于当前数字的数字
*/
public class Solution3 {
// 排序法
public int[] smallerNumbersThanCurrent(int[] nums) {
int len = nums.length; // 定义数组长度
int[] res = Arrays.copyOf(nums, len); // 定义统计结果数组
// 定义map记录每个元素有多少个比它小的数字 Map<item,cnt>
HashMap<Integer, Integer> map = new HashMap<>();
// ① 排序:对res数组元素进行排序(从小到大)
Arrays.sort(res);
// ② 统计:对排序后的res数组进行遍历,记录每个元素对应的比它小的数字个数
for (int i = 0; i < len; i++) {
if (!map.containsKey(res[i])) { // 如果遇到了相同的数字,则不需要更新该数字的统计情况(处理重复元素的情况)
map.put(res[i], i);
}
}
// ③ 更新:遍历res数组(重新更新res),根据map处理结果集
for (int i = 0; i < res.length; i++) {
res[i] = map.get(nums[i]);
}
// 返回处理结果
return res;
}
}
🟢941-有效的山脉数组
1.题目内容
给定一个整数数组 arr,如果它是有效的山脉数组就返回 true,否则返回 false。
让我们回顾一下,如果 arr 满足下述条件,那么它是一个山脉数组:
arr.length >= 3- 在
0 < i < arr.length - 1条件下,存在i使得:arr[0] < arr[1] < ... arr[i-1] < arr[i]arr[i] > arr[i+1] > ... > arr[arr.length - 1]
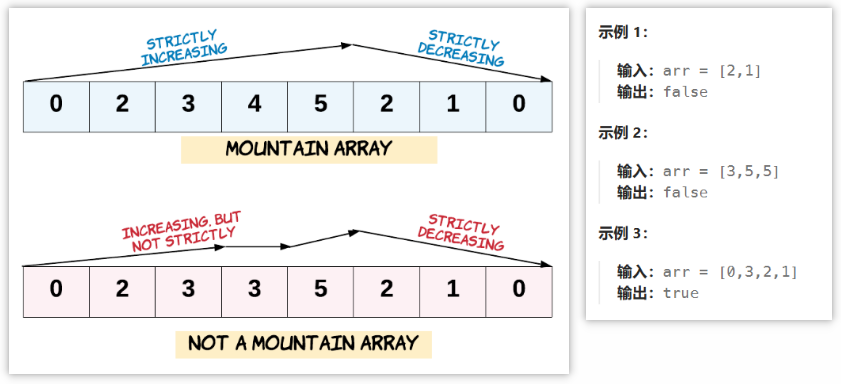
2.题解思路
👻方法1:规律法
思路分析:遍历数组元素,校验每种坡可能出现的情况是否匹配题目(
上坡+下坡构成山脉,且只能有一个上坡和一个下坡)- 遍历元素,比较相邻两个元素的大小以判断坡(数组长度需大于3才可能构成山脉)
arr[i-1]<arr[i]:出现上坡,可连续,但不能再次出现连续上坡(通过记录maxIdx上坡定点,如果在i-maxIdx>2的位置再再次出现上坡则说明不只一次出现)arr[i-1]=arr[i]:出现平坡,一定不满足arr[i-1]>arr[i]:出现下坡,则判断是否出现上坡,进而确定是否可构成山脉- 且不可以出现连续山脉,即上坡和下坡只能出现一次,必须先上后下构成山脉
/** * 🟢 941 有效的山脉 */ public class Solution1 { // 规律法校验:校验各种坡度 public boolean validMountainArray(int[] arr) { int len = arr.length; if (len < 3) { return false; // 元素个数小于3无法构成山脉 } // 判断上升趋势和下降趋势 boolean up = false, down = false; int maxIdx = -1; // 记录最大元素的出现位置 for (int i = 1; i < len; i++) { if (arr[i] > arr[i - 1]) { if (down || i - maxIdx > 2) { // 如果已经出现过下降趋势,或者再次出现了上升趋势,则不符合 return false; } else { // 出现上升趋势 up = true; maxIdx = i; } } else if (arr[i] == arr[i - 1]) { // 出现平坡 return false; // 出现平坡一定不满足 } else { // 出现下降趋势 if (up) { down = true; } } } return up && down; } }- 遍历元素,比较相邻两个元素的大小以判断坡(数组长度需大于3才可能构成山脉)
复杂度分析
时间复杂度:O(n)遍历数组
空间复杂度:O(1)常数级别的空间复杂度占用
需注意此处规律是根据坡的出现情况来分析,例如不可以出现平坡、必须先下后上、上坡和下坡只能有1个等等限制
👻方法2:线性扫描
- 思路分析:基于模拟的方式,和【方法1】中的思路类似,不过此处是基于扫描的概念
- ① 从左到右扫描上坡,得到可能的最大值索引位置
maxIdx(maxIdx不能为数组的第一个或者最后一个位置) - ② 继续从
maxIdx+1的位置出发,判断连续下坡,如果无法走到最后(或者连续下坡被打断则直接返回false),则说明无法构成山脉
- ① 从左到右扫描上坡,得到可能的最大值索引位置
/**
* 🟢 941 有效的山脉
*/
public class Solution2 {
// 规律法校验:校验各种坡度
public boolean validMountainArray(int[] arr) {
int len = arr.length;
if (len < 3) {
return false; // 元素个数小于3无法构成山脉
}
// ① 扫描连续上坡,得到maxIdx
int maxIdx = 0;
for (int i = 1; i < len; i++) {
if (arr[i - 1] > arr[i]) {
// 当出现断层则记录maxIdx位置,跳出遍历
maxIdx = i - 1;
break;
} else if (arr[i - 1] == arr[i]) {
// 出现平坡,不满足
return false;
}
}
// maxIdx 的位置不能出现在arr的首、尾
if (maxIdx == 0 || maxIdx == len - 1) {
return false;
}
// ② 继续从maxIdx+1位置扫描连续下坡,如果出现断层则无法构成山脉
for (int i = maxIdx + 1; i < len; i++) {
if (arr[i - 1] <= arr[i]) {
return false; // 出现断层(平坡或上坡)
}
}
// 满足条件
return true;
}
public static void main(String[] args) {
int[] nums = new int[]{0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
Solution2 s = new Solution2();
s.validMountainArray(nums);
}
}
复杂度分析
时间复杂度:O(n)一次扫描
空间复杂度:O(n)定义
res[]存储结果
👻方法3:双指针
- 思路分析:分别定义两个指针从前往后遍历、从后往前遍历(和【方法2】思路类似)
left指针:处理上坡(遇到平坡或者下降则停止遍历,记录当前位置)right指针:处理下坡(遇到平坡或者上升则停止遍历,记录当前位置)- 指针校验:如果
left和right此时都指向同一个位置且非指向数组的头、尾位置
/**
* 🟢 941 有效的山脉
*/
public class Solution3 {
// 规律法校验:校验各种坡度
public boolean validMountainArray(int[] arr) {
int len = arr.length;
if (len < 3) {
return false; // 元素个数小于3无法构成山脉
}
// 构建双指针分别从首尾遍历(注意数组越界问题处理,确认指针遍历范围)
int left = 0, right = len - 1;
while (left < len - 1 && arr[left] < arr[left + 1]) {
left++;
}
while (right > 0 && arr[right] < arr[right - 1]) {
right--;
}
// 校验left、right是否指向同一个位置,且非指向首、尾位置
if (left == right && left != 0 && right != len - 1) {
return true;
}
return false;
}
}
复杂度分析
时间复杂度:O(n)遍历一遍数组元素
空间复杂度:O(1)定义两个指针辅助遍历,占用常量级空间
🟢1027-独一无二的出现次数
1.题目内容
给你一个整数数组 arr,如果每个数的出现次数都是独一无二的,就返回 true;否则返回 false。
2.题解思路
👻方法1:统计 + 哈希
- 思路分析:先统计每个元素的出现次数,封装为
Map<Integer,Integer>({元素,出现次数})。然后判断出现次数是否重复出现(那么可以基于哈希表去实现)
/**
* 🟢 1207 独一无二的出现次数
*/
public class Solution1 {
// 统计 + 哈希
public boolean uniqueOccurrences(int[] arr) {
// 定义map存储每个元素的出现次数
Map<Integer, Integer> map = new HashMap<>();
for (int cur : arr) {
map.put(cur, map.getOrDefault(cur, 0) + 1);
}
// 遍历map,判断每个数的出现次数是否为独一无二的
Set<Integer> set = new HashSet<>(); // 存储出现次数(如果校验出现重复的出现次数,说明非独一无二)
for (Map.Entry<Integer, Integer> entry : map.entrySet()) {
if (set.contains(entry.getValue())) {
return false;
}
// 当前次数还没出现,加入set集合
set.add(entry.getValue());
}
// 校验通过说明满足
return true;
}
}
复杂度分析
- 时间复杂度:O(2×n)需遍历一遍数组,然后遍历一遍构造的
map - 空间复杂度:O(2×n)此处需借助
map统计元素出现次数,还需借助set辅助校验出现次数是否重复出现
- 时间复杂度:O(2×n)需遍历一遍数组,然后遍历一遍构造的
🟢283-移动零
1.题目内容
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
请注意 ,必须在不复制数组的情况下原地对数组进行操作。
示例 1:
输入: nums = [0,1,0,3,12]
输出: [1,3,12,0,0]
示例 2:
输入: nums = [0]
输出: [0]
2.题解思路
👻方法1:遍历法(❌非原地算法)
- 思路分析:常规解题思路就是暴力遍历法,定义
res数组辅助存储结果,一次遍历将非零元素进行填充并统计0的个数,当nums数组遍历完成则根据0的个数在末尾补0即可
/**
* 🟢 283 移动零
*/
public class Solution1 {
// 遍历法
public void moveZeroes(int[] nums) {
int len = nums.length;
// 定义辅助数组存储结果
int[] res = new int[len];
int idx = 0; // 记录新数组填充位置
int cnt = 0; // 统计0的个数
for (int i = 0; i < len; i++) {
if (nums[i] != 0) {
res[idx++] = nums[i];
} else {
cnt++;
}
}
// 尾部补0
while (cnt-- > 0) {
res[idx++] = 0;
}
// 将数组填充回原数组
for (int i = 0; i < len; i++) {
nums[i] = res[i];
}
}
}
复杂度分析
时间复杂度:O(2×n)需遍历两次数组
空间复杂度:O(n)需借助额外数组空间辅助
👻方法2:双指针法
思路分析:
- 常见误区:此处cue到双指针,可能会习惯性的定义
首尾指针对向遍历,但是此处如果定义了首尾指针对向遍历的话,则可能会导致数组元素顺序被打乱
/** * 🟢 283 移动零 */ public class Solution2 { // 双指针法(首尾指针、对向遍历❌❌会打乱元素本身的顺序) public void moveZeroes(int[] nums) { int len = nums.length; // 定义辅助数组存储结果 int left = 0, right = len - 1; // 定义双指针分别从头尾出发(left寻找为0的元素,right寻找不为0的元素,然后进行交换) // 遍历数组 while (left < right) { // 满足条件则可以将两边元素进行交换 if (nums[left] == 0 && nums[right] != 0) { int temp = nums[left]; nums[left] = nums[right]; nums[right] = temp; // 交换完成,指针继续移动 left++; right--; }else{ // left 用于寻找元素0(遇到非0元素则跳过) if (nums[left] != 0) { left++; } // right 用于寻找非0元素(遇到0元素则跳过) if (nums[right] == 0) { right--; } } } } } // output nums[]:[0,1,0,3,12] =>res[]:[12,1,3,0,0] =>预期结果:[1,3,12,0,0]- 正确思路:应该定义同向的指针同时出发,往前覆盖(与【027-移除元素】的思路类似)
/** * 🟢 283 移动零 */ public class Solution3 { // 双指针法 public void moveZeroes(int[] nums) { int len = nums.length; // 定义辅助数组存储结果 int slowIdx = 0; // 定义同向指针同时出发,往前覆盖 for (int fastIdx = 0; fastIdx < len; fastIdx++) { if (nums[fastIdx] != 0) { nums[slowIdx++] = nums[fastIdx]; // 覆盖 } } // 上述遍历完成,继续从slowIdx指向位置出发填充剩余的0(因为移除的元素为0,所以直接覆盖即可) for (int i = slowIdx; i < len; i++) { nums[i] = 0; } } }- 常见误区:此处cue到双指针,可能会习惯性的定义
复杂度分析
时间复杂度:O(n)
空间复杂度:O(1)
🟡189-旋转数组
todo:https://programmercarl.com/0189.%E6%97%8B%E8%BD%AC%E6%95%B0%E7%BB%84.html
1.题目内容
给定一个整数数组 nums,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。
示例 1:
输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右轮转 1 步: [7,1,2,3,4,5,6]
向右轮转 2 步: [6,7,1,2,3,4,5]
向右轮转 3 步: [5,6,7,1,2,3,4]
示例 2:
输入:nums = [-1,-100,3,99], k = 2
输出:[3,99,-1,-100]
解释:
向右轮转 1 步: [99,-1,-100,3]
向右轮转 2 步: [3,99,-1,-100]
2.题解思路
结合上述题示意案例分析,此处需注意k的轮次概念,当k%len=0的时候相当于没有反转,因此真正的反转轮次应该为k=k%len,随后分析反转规律来处理数组
👻方法1:遍历法(非原地算法)
- 思路分析:基于反转后的数组分析,反转k次的概念实际上就是将原数组
nums的后k个元素提到数组前面,那么可以采取遍历的思路封装res[],先遍历后k个元素(即[len-k,len-1]),然后遍历前n-k个元素(即[0,len-k-1])
/**
* 🟡189 轮转数组
*/
public class Solution2 {
// 遍历
public void rotate(int[] nums, int k) {
int len = nums.length;
k = k % len; // 获取真正需要的轮转次数
// 根据题意分析向右轮转k次,实际上就是将元素末尾k个元素提到数组前面
int[] res = new int[len];
int idx = 0;// idx指向当前数组填充位置
// 先遍历后k个元素
for (int i = len - k; i < len; i++) {
res[idx++] = nums[i];
}
// 再遍历前n-k个元素
for (int i = 0; i < len - k; i++) {
res[idx++] = nums[i];
}
// 数组回填
for (int i = 0; i < len; i++) {
nums[i] = res[i];
}
}
}
复杂度分析
- 时间复杂度:O(n)
- 空间复杂度:O(n)需借助辅助数组进行填充,然后回填nums
👻方法2:三次反转法(原地算法)
- 思路:同理,观察反转规则,可以发现反转
k次得到的结果可以经过三次反转得到结果- 以
1 2 3 4 5 6 7,k=3为例 - 第1次反转:全数组反转 =》
7 6 5 4 3 2 1 - 第2次反转:前K个元素反转 =》
5 6 7 4 3 2 1 - 第3次反转:后N-K个元素反转 =》
5 6 7 1 2 3 4得到最终结果
- 以
/**
* 🟡189 轮转数组
*/
public class Solution1 {
// 三次反转
public void rotate(int[] nums, int k) {
int len = nums.length;
k = k % len; // 获取真正需要的轮转次数
// 基于反转的概念:对整个数组进行反转,对前k反转,对后n-k个元素进行反转
reverse(nums, 0, len - 1);// 对整个数组进行反转[0,len-1]
reverse(nums, 0, k - 1); // 对前k个元素进行反转[0,k-1]
reverse(nums, k, len - 1); // 对后n-k个元素进行反转[k,n-1]
}
// 定义方法:限定对指定区域范围的数组元素进行反转
public void reverse(int[] nums, int start, int end) { // 此处限定取值范围为[start,end]
while (start < end) {
int temp = nums[start];
nums[start] = nums[end];
nums[end] = temp;
// 反转完成,指针靠拢
start++;
end--;
}
}
}
复杂度分析
时间复杂度:O(n)
空间复杂度:O(1)原地算法
🟢724-寻找数组的中心索引
1.题目内容
给你一个整数数组 nums ,请计算数组的 中心下标 。
数组 中心下标 是数组的一个下标,其左侧所有元素相加的和等于右侧所有元素相加的和。
如果中心下标位于数组最左端,那么左侧数之和视为 0 ,因为在下标的左侧不存在元素。这一点对于中心下标位于数组最右端同样适用。
如果数组有多个中心下标,应该返回 最靠近左边 的那一个。如果数组不存在中心下标,返回 -1 。
示例 1:
输入:nums = [1, 7, 3, 6, 5, 6]
输出:3
解释:
中心下标是 3 。
左侧数之和 sum = nums[0] + nums[1] + nums[2] = 1 + 7 + 3 = 11 ,
右侧数之和 sum = nums[4] + nums[5] = 5 + 6 = 11 ,二者相等。
示例 2:
输入:nums = [1, 2, 3]
输出:-1
解释:
数组中不存在满足此条件的中心下标。
示例 3:
输入:nums = [2, 1, -1]
输出:0
解释:
中心下标是 0 。
左侧数之和 sum = 0 ,(下标 0 左侧不存在元素),
右侧数之和 sum = nums[1] + nums[2] = 1 + -1 = 0 。
2.题解思路
👻方法1:暴力搜索
- 思路分析:基于题意拆解,遍历每个元素(每个元素都可能作为中心下标位置),分别计算元素当前遍历元素左侧所有的值之和
leftSum,然后判断元素右侧是否存在当前遍历元素右侧所有的值之和rightSum等于leftSum,如果存在则直接返回满足条件的中心下标位置,否则继续下个位置的处理
/**
* 🟢724 寻找数组的中心下标
*/
public class Solution1 {
// 遍历:判断每个下标
public int pivotIndex(int[] nums) {
int len = nums.length;
for (int i = 0; i < len; i++) {
// 校验每个元素位置i是否符合中心坐标的定义,一旦找到直接返回,否则继续搜索
int leftSum = 0; // 存储 i 左侧的元素总和
for (int left = 0; left < i; left++) {
leftSum += nums[left];
}
int rightSum = 0; // 存储 i 右侧的元素总和
for (int right = i + 1; right < len; right++) {
rightSum += nums[right];
}
// 判断leftSum==rightSum是否成立
if (leftSum == rightSum) {
return i; // 找到满足条件的中心坐标则直接返回
}
}
// 没有匹配的内容
return -1;
}
}
复杂度分析
时间复杂度:O(n2)基于上述中规中矩的暴力搜索,可以发现,每次校验一个元素位置,都要分别计算其左、右侧元素总和,每次都是从头到尾计算一遍。时间复杂度较高
空间复杂度:O(1)
👻方法2:搜索 + 时间优化(空间换时间)
- 思路分析:基于上述代码实现可以看到,对于每个可能的中心下标位置,都会对其左侧、右侧所有元素的总和进行计算,那么就会导致重复计算和的情况。基于实际上题意就是为了求解前缀和、后缀和是否相等,因此可以采用动态规划的思路优化,用空间换时间,优化检索效率
/**
* 🟢724 寻找数组的中心下标
*/
public class Solution3 {
// 遍历:判断每个下标(空间换时间,分别计算每个元素的前缀和、后缀和)
public int pivotIndex(int[] nums) {
int len = nums.length;
// 分别定义每个元素位置的前缀和、后缀和数组
int[] leftSum = new int[len], rightSum = new int[len];
leftSum[0] = 0; // 第一个元素的左边没有元素,所以前缀和为0
rightSum[len - 1] = 0; // 最后一个元素右边没有元素,所以后缀和为0
// 正序遍历:计算前缀和
for (int i = 1; i < len; i++) {
leftSum[i] = leftSum[i - 1] + nums[i - 1];
}
// 逆序遍历:计算后缀和
for (int i = len - 2; i >= 0; i--) {
rightSum[i] = rightSum[i + 1] + nums[i + 1];
}
// 遍历元素,验证每个坐标是否满足对应位置的前缀和=后缀和
for (int i = 0; i < len; i++) {
if (leftSum[i] == rightSum[i]) {
return i;
}
}
// 没有匹配的内容
return -1;
}
}
复杂度分析
时间复杂度:O(3×n),一遍计算前缀和、一遍计算后缀和、一遍验证每个位置上是否存在前缀和与后缀和相等的情况
空间复杂度:O(2×n),需要构建辅助数组分别存储前缀和、后缀和
优化后的效率对比:
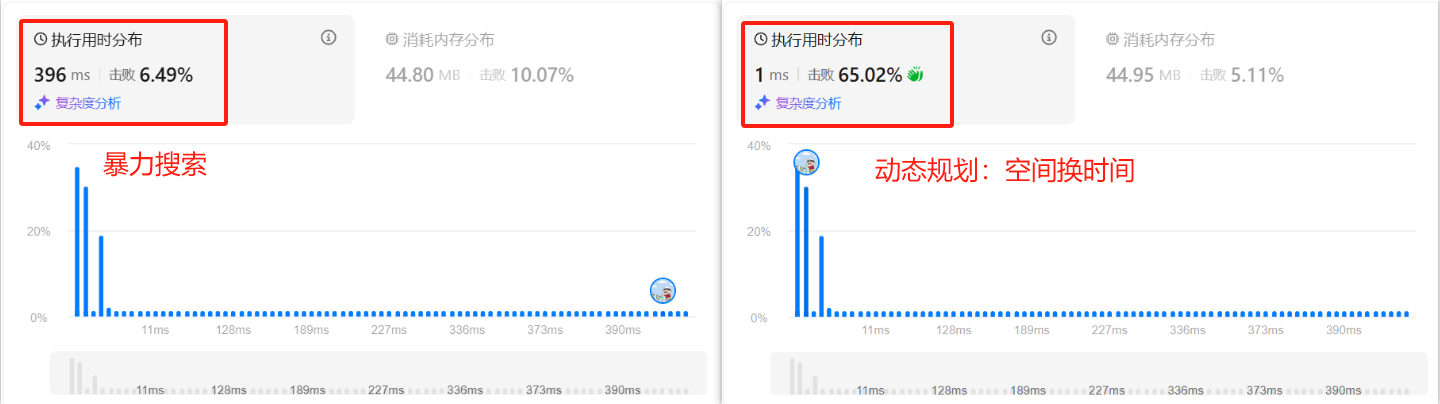
👻方法2:两次遍历思路
- 思路分析:基于上述思路,此处可以进一步优化遍历技巧,因为每次计算都是元素左侧、右侧各自所有的元素,因此实际上当已知总和
totalSum和leftSum那么就能得到rightSum(rightSum=totalSum-leftSum),基于此实际可以通过两次遍历就可以得到答案
/**
* 🟢724 寻找数组的中心下标
*/
public class Solution3 {
// 两次遍历:totalSum、leftSum、rightSum
public int pivotIndex(int[] nums) {
int len = nums.length;
// 定义数组元素总和
int totalSum = 0;
for (int num : nums) {
totalSum += num;
}
// 定义当前遍历元素左侧所有元素的总和
int leftSum = 0;
for (int i = 0; i < len; i++) {
// 校验当前的rightSum
int rightSum = totalSum - leftSum - nums[i];
// 判断当前的leftSum是否等于rightSum
if (leftSum == rightSum) {
return i;
}
// 更新leftSum(继续下一轮校验)
leftSum += nums[i];
}
// 没有匹配的内容
return -1;
}
}
复杂度分析
- 时间复杂度:O(2×n)一次遍历计算总和
totalSum,一次遍历计算leftSum的同时得到rightSum,然后校验leftSum==rightSum是否成立 - 空间复杂度:O(1)常数级别的空间复杂度占用
- 时间复杂度:O(2×n)一次遍历计算总和
🟡034-在排序数组中查找元素的第一个和最后一个位置
1.题目内容
给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回 [-1, -1]。
你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
输入:nums = [5,7,7,8,8,10], target = 8
输出:[3,4]
示例 2:
输入:nums = [5,7,7,8,8,10], target = 6
输出:[-1,-1]
示例 3:
输入:nums = [], target = 0
输出:[-1,-1]
2.题解思路
👻方法1:暴力搜索(顺序普通搜索)
- 思路分析:数组本身有序,因此只需要找到第一个
target,然后从这个位置出发进行内层循环统计target出现的次数即可得到target最终出现的位置(需注意数组有效范围的处理,元素取值等)
/**
* 🟡 034 在排序数组中查找元素的第一个和最后一个位置
*/
public class Solution1 {
/**
* 遍历搜索
*/
public int[] searchRange(int[] nums, int target) {
int len = nums.length;
// 数组本身有序,因此可以正序搜索找到target,统计这个元素出现的次数即可(注意数组下标的处理)
for (int i = 0; i < len; i++) {
if (nums[i] == target) {
// 从当前i位置开始搜索
int cnt = 0;
for (int j = i; j < len; j++) {
if (nums[i] == nums[j]) {
cnt++;
}
}
return new int[]{i, i + cnt - 1}; // j从i开始计数,因此此处索引统计要减1
}
}
return new int[]{-1, -1};
}
}
复杂度分析
时间复杂度:O(n)
空间复杂度:O(1)
👻方法2:二分搜索target + 定位左右边界
题目限定O(logN)的时间复杂度,由此基于有序数组可以联想到二分法检索:此处二分法也有多种解法切入
- 思路分析:数组存在重复元素且有序,因此可以采用【二分搜索
target+ 定位左右边界】的思路进行处理- ① 基于二分法定位
target所在的索引位置idx(如果idx存在则进行下一步边界寻找,如果idx不存在则不需要再检索) - ② 分别基于
idx往左、往右寻找左右边界
- ① 基于二分法定位
/**
* 🟡 034 在排序数组中查找元素的第一个和最后一个位置
*/
public class Solution2 {
/**
* 二分搜索 + 左右边界寻找
*/
public int[] searchRange(int[] nums, int target) {
int len = nums.length;
// ① 数组本身有序,基于二分法搜索target位置idx
int idx = binarySearch(nums, target);
if (idx == -1) {
return new int[]{-1, -1}; // target不存在
}
// ② 如果idx存在则分别向左、向右寻找其左右边界
int left = idx, right = idx; // left、right初始化为idx位置
while (left - 1 >= 0 && nums[left - 1] == target) { // 从idx的前一个位置开始校验
left--;
}
while (right + 1 < len && nums[right + 1] == target) {// 从idx的后一个位置开始校验
right++;
}
return new int[]{left, right};
/*
int left = idx, right = idx; // left、right初始化为idx位置
while (left >= 0 && nums[left] == target) {
left--;
}
while (right < len && nums[right] == target) {
right++;
}
return new int[]{left + 1, right - 1}; // 返回结果去掉`idx`位置的讨论
*/
}
// 传入有序的nums[],获取target所在索引位置,如果不存在返回-1
public int binarySearch(int[] nums, int target) {
int left = 0, right = nums.length - 1; // 闭区间取值
while (left <= right) {
int mid = (right - left) / 2 + left; // (left + right) / 2
// 比较target和中间位置元素
if (target < nums[mid]) {
// target 在左侧,右侧缩边
right = mid - 1;
} else if (target > nums[mid]) {
// target 在右侧,左侧缩边
left = mid + 1;
} else {
return mid;
}
}
// 不存在target
return -1;
}
public static void main(String[] args) {
int[] nums = new int[]{5, 7, 7, 8, 8, 10};
Solution2 s = new Solution2();
s.searchRange(nums, 8);
}
}
复杂度分析
时间复杂度:O(logN),这种思路如果重复的target太多,则通过
idx向左右两边检索的话会慢慢退化为O(N)时间复杂度空间复杂度:O(1)
👻方法3:二分法直接确定左右边界,校验边界关系
- 思路分析:另一种二分法处理思路,就是直接调用两次二分法,分别寻找左、右边界,校验得到的左右边界的关系
- 情况1:
target在数组范围内的左边或者右边- 例如
{3,4,5},求target为2或者6,此时应该返回{-1,-1}
- 例如
- 情况2:
target在数组范围中,且数组中不存在target- 例如
{3,6,7},求target为5,此时应该返回{-1,-1}
- 例如
- 情况3:
target在数组范围中,且数组中不存在target- 例如
{3,6,7},求target为6,此时应该返回{1,1}
- 例如
- 情况1:
/**
* 🟡 034 在排序数组中查找元素的第一个和最后一个位置
*/
public class Solution3 {
/**
* 直接使用二分搜索定位左右边界,然后校验左右边界的索引关系
*/
public int[] searchRange(int[] nums, int target) {
int len = nums.length;
// ① 分别调用二分检索获取到左右边界
int leftBorder = binarySearchLeftBorder(nums, target);
int rightBorder = binarySearchRightBorder(nums, target);
// ② 校验左右边界索引关系:如果左右边界指向索引有一个不存在,则说明target不存在
if (leftBorder == -2 || rightBorder == -2) { // 此处设定为-2
return new int[]{-1, -1};
}
if (rightBorder - leftBorder > 1) {
return new int[]{leftBorder + 1, rightBorder - 1};
}
return new int[]{-1, -1};
}
// 传入有序的nums[],获取target所在索引位置,如果不存在返回-1
public int binarySearchLeftBorder(int[] nums, int target) {
int left = 0, right = nums.length - 1; // 闭区间取值
int leftBorder = -2;
while (left <= right) {
int mid = (right - left) / 2 + left; // (left + right) / 2
// 比较target和中间位置元素
if (target <= nums[mid]) {
right = mid - 1; // target 在左侧,右侧缩边
leftBorder = right; // 寻找左边界
} else if (target > nums[mid]) {
// target 在右侧,左侧缩边
left = mid + 1;
}
}
return leftBorder;
}
// 传入有序的nums[],获取target所在索引位置,如果不存在返回-1
public int binarySearchRightBorder(int[] nums, int target) {
int left = 0, right = nums.length - 1; // 闭区间取值
int rightBorder = -2;
while (left <= right) {
int mid = (right - left) / 2 + left; // (left + right) / 2
// 比较target和中间位置元素
if (target < nums[mid]) {
right = mid - 1;// target 在左侧,右侧缩边
} else if (target >= nums[mid]) {
left = mid + 1; // target 在右侧,左侧缩边
rightBorder = left; // 寻找右边界
}
}
return rightBorder;
}
public static void main(String[] args) {
int[] nums = new int[]{5, 7, 7, 8, 8, 10};
Solution3 s = new Solution3();
s.searchRange(nums, 8);
}
}
复杂度分析
- 时间复杂度:O(2 × logN)两次二分法检索分别定位左、右边界
- 空间复杂度:O(1)常数级别空间占用
👻方法4:工具类(转为List处理)
- 思路分析:将数组元素转化为
List存储,然后借助提供的方法调用
public int[] searchRange(int[] nums, int target) {
List<Integer> list = new ArrayList<>(nums.length);
for (int num : nums) {
list.add(num);
}
return new int[]{list.indexOf(target), list.lastIndexOf(target)};
}
复杂度分析
时间复杂度:O(n)
空间复杂度:O(n)将
nums[]转化为list处理
🟢922-按奇偶排序数组II
1.题目内容
给定一个非负整数数组 nums, nums 中一半整数是 奇数 ,一半整数是 偶数 。
对数组进行排序,以便当 nums[i] 为奇数时,i 也是 奇数 ;当 nums[i] 为偶数时, i 也是 偶数 。
你可以返回 任何满足上述条件的数组作为答案 。
示例 1:
输入:nums = [4,2,5,7]
输出:[4,5,2,7]
解释:[4,7,2,5],[2,5,4,7],[2,7,4,5] 也会被接受。
示例 2:
输入:nums = [2,3]
输出:[2,3]
2.题解思路
👻方法1:分类遍历法(一次遍历分类、一次遍历封装)
- 思路分析:
- ① 第1次遍历:分别找到奇数、偶数,并封装到对应的集合(
size相同) - ② 第2次遍历:根据
i确定封装规律,将奇数封装到奇数索引位置,偶数封装到偶数索引位置(i属于[0,len/2))- 奇数下标
2*i偶数下标2*i+1
- 奇数下标
- ① 第1次遍历:分别找到奇数、偶数,并封装到对应的集合(
/**
* 🟢 922 按照奇偶排序数组II
*/
public class Solution1 {
// 分类遍历法
public int[] sortArrayByParityII(int[] nums) {
int len = nums.length;
// 分别定义两个集合存储奇数、偶数列表
List<Integer> oddNums = new ArrayList<>();
List<Integer> evenNums = new ArrayList<>();
// 遍历数组封装奇数、偶数
for (int num : nums) {
if (num % 2 == 1) {
oddNums.add(num);
} else if (num % 2 == 0) {
evenNums.add(num);
}
}
// 封装结果集
int[] res = new int[len];
// 分别填充奇数、偶数
for (int i = 0; i < len / 2; i++) { // 奇数偶数对半
res[2 * i] = evenNums.get(i);
res[2 * i + 1] = oddNums.get(i);
}
// 返回结果
return res;
}
}
复杂度分析
时间复杂度:O(n)需遍历两次(一次处理奇偶数,一次处理结果集)
空间复杂度:O(n)需借助辅助集合存储奇偶数
👻方法2:双指针法
- 思路分析:此处可以联想到指针处理(区分遍历、处理)
- ① 指针定义:定义两个指针
oddIdx、evenIdx分别指向res[]的奇数位、偶数位下标,定义一个指针用于遍历nums数组 - ② 一次遍历:遍历
nums数组,判断nums[i]为奇数还是偶数,将其放置在指定的位置,并更新下标即可
- ① 指针定义:定义两个指针
/**
* 🟢 922 按照奇偶排序数组II
*/
public class Solution2 {
// 指针法:双指针分别指向res用于指向存储奇数、偶数的下标位置,一个指针用于遍历元素判断奇偶
public int[] sortArrayByParityII(int[] nums) {
int len = nums.length;
// 分别定义奇数、偶数存储的下标指针
int oddIdx = 1;
int evenIdx = 0;
// 定义结果集
int[] res = new int[len];
// 遍历数组封装奇数、偶数
for (int i = 0; i < len; i++) {
// 遍历每个元素判奇偶,然后将其放置在对应的位置
if (nums[i] % 2 == 0) {
// 放置在偶数位置,随后更新evenIdx(指向下一个存放位置)
res[evenIdx] = nums[i];
evenIdx += 2; // 向前移动两位
} else if (nums[i] % 2 == 1) {
// 放置在奇数位置,随后更新oddIdx(指向下一个存放位置)
res[oddIdx] = nums[i];
oddIdx += 2;
}
}
// 返回结果
return res;
}
}
复杂度分析
时间复杂度:O(n)只需要遍历一次数组
空间复杂度:O(1)占用常数级别空间
🟢035-搜索插入位置(二分模板基础题型)
1.题目内容
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
请必须使用时间复杂度为 O(log n) 的算法。
2.题解思路
👻方法1:搜索O(n)
- 思路分析:正序遍历有序数组,如果出现
>=target的位置即为所得
/**
* 🟢035 搜索插入位置
*/
public class Solution0 {
// 二分法(左闭右开)
public int searchInsert(int[] nums, int target) {
for (int i = 0; i < nums.length; i++) {
/**
* 如果cur=target说明当前遍历位置即为target位置,即返回i
* 如果cur>target说明出现了没找到target,那么当前这个第一个大于target的位置就是target要插入的位置,所以也是返回i
*/
if (nums[i] >= target) {
return i;
}
}
// 如果不存在大于等于target的数,则说明target最大,直接插入到数组尾部
return nums.length;
}
}
复杂度分析
时间复杂度:O(n)
空间复杂度:O(1)
👻方法2:二分法 O(log n)
/**
* 🟢035 搜索插入位置
*/
public class Solution {
// 二分法(闭区间)
public int searchInsert1(int[] nums, int target) {
int left = 0, right = nums.length - 1; // 闭区间
while (left <= right) {
int mid = left + (right - left) / 2; // 避免溢出(left+right)/2
// 判断target与nums[mid]的关系
if (target < nums[mid]) {
right = mid - 1;
} else if (target > nums[mid]) {
left = mid + 1;
} else if (target == nums[mid]) {
return mid; // 找到目标值
}
}
// 如果目标值不存在可以返回-1进行标记,此处如果要返回插入位置则选择left
return left;
}
// 二分法(开区间)
public int searchInsert2(int[] nums, int target) {
int left = -1, right = nums.length; // 开区间
while (left + 1 < right) {
int mid = left + (right - left) / 2; // 避免溢出(left+right)/2
// 判断target与nums[mid]的关系
if (target < nums[mid]) {
right = mid;
} else if (target > nums[mid]) {
left = mid;
} else if (target == nums[mid]) {
return mid; // 找到目标值
}
}
// 返回下一个插入索引位置
return right;
}
// 二分法(左闭右开)
public int searchInsert3(int[] nums, int target) {
int left = 0, right = nums.length; // 开区间
while (left < right) {
int mid = left + (right - left) / 2; // 避免溢出(left+right)/2
// 判断target与nums[mid]的关系
if (target < nums[mid]) {
right = mid;
} else if (target > nums[mid]) {
left = mid + 1;
} else if (target == nums[mid]) {
return mid; // 找到目标值
}
}
// 返回下一个插入索引位置
return left;
}
}
复杂度分析
时间复杂度:O(logN)
空间复杂度:O(1)
07-区间和
1.题目内容
本题非leetcode,扩展补充题型
给定一个整数数组 Array,请计算该数组在每个指定区间内元素的总和。
输入描述:第一行输入为整数数组 Array 的长度 n,接下来 n 行,每行一个整数,表示数组的元素。随后的输入为需要计算总和的区间,直至文件结束。
输出描述:输出每个指定区间内元素的总和。
2.题解思路
👻方法1:累加和 或 前缀和思路
- 思路分析
- 【1】累加和:根据区间索引计算累加和(如果需要计算多个区间,则需重复计算,这个效率是相对比较低下的)
- 【2】前缀和:定义数组维护前缀和(此处前缀和设定累加到当前元素),将区间和转化为
dp[end]-dp[start-1](前缀和的差值),以此优化多区间重复计算效率
/**
* 数组篇:07 区间和
* 给定数组和指定要计算的区间,返回区间和
*/
public class Solution1 {
// 方式1:根据区间计算累加和
public int getIntervalSum1(int[] nums, int start, int end) {
int sum = 0;
// 根据区间索引计算累加和
for (int i = start; i <= end; i++) {
sum += nums[i];
}
// 返回区间累加和
return sum;
}
// 方式2:前缀和(定义数组dp[] 指定位置上存储元素的前缀和)
public int getIntervalSum2(int[] nums, int start, int end) {
int len = nums.length;
// 定义dp数组存储前缀和(此处的前缀和包括当前元素的累加和)
int[] dp = new int[len];
dp[0] = nums[0]; // 初始化
for (int i = 1; i < len; i++) {
dp[i] = dp[i - 1] + nums[i];
}
// 返回指定区间的前缀和
if (start == 0) {
return dp[end];
} else {
return dp[end] - dp[start - 1]; // 需单独处理start=0的情况避免数组越界
}
}
public static void main(String[] args) {
Solution1 s = new Solution1();
int res1 = s.getIntervalSum1(new int[]{1, 2, 3, 4, 5}, 1, 2);
System.out.println(res1);
int res2 = s.getIntervalSum2(new int[]{1, 2, 3, 4, 5}, 0, 1);
System.out.println(res2);
}
}
复杂度分析
方式1【累加和】
时间复杂度:O(X)X 为区间长度
空间复杂度:O(1)
方式2【前缀和】
时间复杂度:O(N)N为数组长度,需遍历整个数组元素,然后通过前缀和差值的方式获取区间和
空间复杂度:O(N)N为数组长度,需要一个数组维护所有元素位置的前缀和(累加和)
08-开发商购买土地
1.题目内容
2.题解思路
👻方法1:
复杂度分析
时间复杂度:
空间复杂度:
