skill-07-二叉树

holic-x...大约 188 分钟

难度说明：🟢简单🟡中等🔴困难

学习资料

代码随想录open in new window

学习目标

掌握数据结构核心基础
借助数据结构完成常见题型

skill-07-二叉树

理论基础

1.核心理论

（1）二叉树分类

满二叉树：如果一棵二叉树只有度为0的结点和度为2的结点，并且度为0的结点在同一层上，则这棵二叉树为满二叉树

完全二叉树：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层（h从1开始），则该层包含 1~ 2^(h-1) 个节点

优先队列实际是一个堆，堆就是一颗完全二叉树，同时保证父子节点的顺序关系

二叉搜索树：前面介绍的树，都没有数值的，而二叉搜索树是有数值的了，二叉搜索树是一个有序树。

若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
它的左、右子树也分别为二叉排序树

平衡二叉树：每个节点的左子树和右子树的深度相差不超过1

所谓平衡是针对同一个节点的左右子树的高度校验，例如下图案例中图示②中c和h节点虽然高度差相差2，但是这个还是一个平衡二叉树（因为是要对同一个节点的左右子树校验）

平衡二叉搜索树：AVL（Adelson-Velsky and Landis）树，且具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树

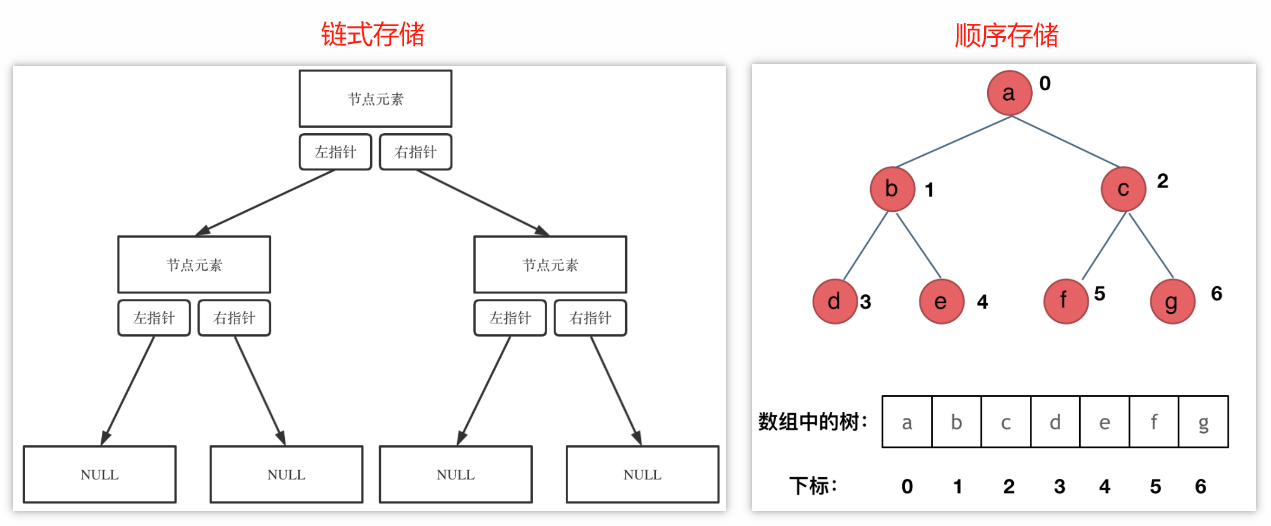
（2）二叉搜索树的存储方式

链式存储、顺序存储

顺序存储的元素在内存是连续分布的，而链式存储则是通过指针把分布在各个地址的节点串联一起

（3）二叉树的遍历方式

深度优先遍历（前中后针对的是D的位置，L始终在R左侧）
- 前序遍历（递归法，迭代法）：DLR
- 中序遍历（递归法，迭代法）：LDR
- 后序遍历（递归法，迭代法）：LRD
广度优先遍历
- 层次遍历（迭代法）：借助辅助队列进行遍历（从上往下，从左往右依次遍历）

栈和队列的需求

栈其实是递归的一种实现结构，因此此处的前中后序遍历逻辑可以借助栈使用递归的方式实现；

而广度优先遍历的实现一般使用队列实现（需依赖先进先出的结构才能一层一层遍历二叉树）

（4）二叉树的结构定义

树节点结构定义

/**
 * 树节点
 */
public class TreeNode {

    public int val; // 节点值
    public TreeNode left; // 左子节点
    public TreeNode right; // 右子节点

    // 构造函数
    public TreeNode() {

    }

    public TreeNode(int val) {
        this.val = val;
        this.left = null;
        this.right = null;
    }

    public TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

2.技巧总结

（1）二叉树题型分类

二叉树题目分类（特性）：
- ① 普通二叉树：无
- ② 满二叉树：除最后一层之外，其他层节点都占满
- ③ 完全二叉树：节点总个数的计算公式为2^h-1，如果以某个节点为根节点的左右子树高度相同则该节点所在子树为完全二叉树
- ④ 平衡二叉树：节点的左右子树的高度差不超过1
- ⑤ 二叉搜索树：中序遍历（DLR）的序列是升序序列
二叉树的遍历方式：层序遍历（广度优先遍历）、深度优先遍历（前序、中序、后序）
- 144 二叉树的前序遍历（递归法、迭代法）
- 145 二叉树的后序遍历（递归法、迭代法）
- 094 二叉树的中序遍历（递归法、迭代法）
- 102 二叉树的层序遍历（迭代法）
二叉树的属性：
- 101 对称二叉树
- 104 二叉树的最大深度
- 111 二叉树的最小深度
- 222 完全二叉树的节点个数
- 110 平衡二叉树
- 257 二叉树的所有路径
- 404 左叶子之和
- 513 找树左下角的值
- 112 路径总和
二叉树的修改与构造：
- 226 翻转二叉树
- 106 从中序和后续遍历构造二叉树
- 654 最大二叉树
- 617 合并二叉树
二叉搜索树的属性：
- 700 二叉搜索树中的搜索
- 098 验证二叉搜索树
- 530 二叉搜索树的最小绝对差
- 501 二叉搜索树中的众数
- 538 把二叉搜索树转化为累加树
二叉树公共祖先问题：
- 236 二叉树的最近公共祖先
- 235 二叉搜索树的最近公共祖先
二叉搜索树的修改与构造：
- 701 二叉搜索树中的插入操作
- 450 删除二叉搜索树中的节点
- 669 修剪二叉搜索树
- 108 将有序数组转化为二叉搜索树

二叉树的题型要学会举一反三，很多类似题型思路是通用或者层层递进的，理解核心，不要死记硬背

解题技巧：
对于递归解法思路（DFS），先将基础框架回顾一遍，然后分析关系（选择遍历方案DLR、LDR、LRD），将大致框架定下来，然后思考递归规则，思路会更加有条理一点
对于BFS解法思路，先把最基础的BFS遍历罗列出来，然后再思考如何进一步做分层等处理

（2）二叉树题型解题技巧

二叉树题目分类 & 解题技巧：

二叉树的遍历方式：层序遍历（广度优先遍历）、深度优先遍历（前序、中序、后序）
- 144 二叉树的前序遍历（递归法、迭代法）
- 145 二叉树的后序遍历（递归法、迭代法）
- 094 二叉树的中序遍历（递归法、迭代法）
- 102 二叉树的层序遍历（迭代法）
二叉树的属性：
- 101 对称二叉树：BFS、DFS
  - 转化为【两棵树】的对称比较（用两个指针分别遍历树），对应位置节点为一组进行比较，基于遍历的思路处理（对节点进行null情况处理）。这种比较的思路可以用于处理【100-相同的树】、【572-另一棵树的子树】，需注意校验的节点
- 二叉树的深度问题：
  - 104 二叉树的最大深度（树的高度）
    - 回溯法：获取从【根结点->叶子结点】的路径，选择路径中节点最多的情况
    - BFS：基于层序遍历，统计层数（从上到下，从左到右遍历所有节点，统计层数）
    - DFS：基于求节点高度的思路：当前节点最大高度 = max{dfs(leftTree),dfs(rightTree)}+1（选择左、右子树中最大高度的节点 + 1 得到当前节点的最大高度）
  - 111 二叉树的最小深度
    - 回溯法：获取从【根结点->叶子结点】的路径，选择路径中节点最少（路径最短）的情况
    - BFS：基于层序遍历（从上到下，从左到右遍历），找到的第一个叶子结点所在的层数即为所得（第一个遇到的叶子节点）
    - DFS：递归处理，根据node是否为null进行处理（node不为null是需要根据其left、right左右节点的状态进行讨论最小深度会出现在哪个位置）
  - 559 N 叉树的最大深度（也可通过上述三种思路处理，只不过此处处理的是子节点列表，而不局限于左右节点）
- 222 完全二叉树的节点个数
  - DFS：基于DFS思路遍历所有节点并统计个数
    - 思路1：基于深度优先遍历思路遍历所有节点，然后统计节点个数（计数或者加入结果集）
    - 思路2：递归核心为L+R+1，即节点个数 = 左子树节点个数 + 右子树节点个数 + 1 = dfs(leftTree )+ dfs(rightTree) + 1
  - BFS：基于BFS思路遍历所有节点并统计个数
  - DFS优化：递归判断每个节点树是否为完全二叉树，如果是则直接使用公式计算，如果不是则递归遍历计算
    - 基于L+R+1的递归核心，在递归的过程中进行分类统计（区分当前节点所在子树是否为满二叉树）
- 110 平衡二叉树（递归核心：左右子树高度差不超过1，对于任意一个节点，左子树和右子树的高度差不超过1）
  - DFS：转化递归遍历每个节点判断左右子树的高度差不超过1（拆分思路，两个递归处理（一个递归用于遍历节点、一个递归用于获取节点左右子树高度））
    - ① maxDepth方法递归用于计算子树高度
    - ② balance方法递归用于校验左右子树高度差是否超过1（高度差超过1则不平衡，如果平衡则其左右子树也需满足平衡）
  - DFS优化：优化为1个递归方法处理，在递归获取节点高度的时候附带校验左右子树的高度差，如果非平衡则直接返回-1用于标识不平衡（节点递归获取高度如果获取到的高度为-1视作非正常高度，一层层直接往上抛）
- 257 二叉树的所有路径：基于遍历的思路，遍历每个节点记录路径，当遇到叶子节点则记录当前节点路径
  - BFS：构建双队列辅助遍历，一个用于记录节点，一个用于同步记录当前节点拼接的路径，遍历的过程中遇到叶子结点则将相应路径加入结果集
    - nodeQueue节点队列，pathQueue路径队列（同步更新）
  - DFS：基于DFS递归的思路（DLR），遇到叶子结点则将当前路径结果集（注意递归对象引用问题）
  - 回溯：基于回溯的思路处理（参考回溯模板的构建，适用于求解路径问题，推荐使用）
- 404 左叶子之和
  - 左叶子核心：判断一个节点是否存在左叶子（即左节点存在且该左节点为叶子节点：cur.left!=null && cur.left.left==null && cur.left.right==null）
  - BFS：层序遍历，遍历每个节点，如果校验其存在左叶子则累加左叶子之和
  - DFS：递归遍历，类似的基于DLR遍历次序，校验节点是否存在左叶子，并递归遍历左右子树即可
- 513 找树左下角的值
  - BFS：基于层序遍历思路，寻找最后一层的第1个节点（由于无法明确最后1层，因此可以通过收集（收集每1层的第1个节点）或者覆盖的方式获取target）
  - DFS：基于递归遍历的思路，当curLevel大于maxLevel时触发更新（说明到了新的一层），继续递归遍历左右子树（层数下沉1）
    - 核心参数：涉及target（每1层的第1个元素，通过覆盖更新）、maxLevel（当前遍历的最大层数/深度）、curLevel（当前遍历深度）
    - 迭代顺序：无关顺序，主要关注深度的变化
- 112 路径总和
  - 核心：校验是否存在根节点到叶子节点的路径和等于targetSum的路径存在则返回
  - BFS：基于层序遍历思路，构建双队列辅助遍历，当校验到叶子节点则校验当前路径和是否等于targetSum（存在则返回true）
  - DFS：基于递归遍历思路，校验节点是否为叶子节点（如果为叶子节点则进一步校验路径和是否为targetSum），递归遍历左右子树（只要左或右子树存在一条满足的路径即可返回true）
二叉树的修改与构造：
- 226 翻转二叉树：BFS、DFS
  - 转化为【遍历】的思路，遍历每个节点并交换节点的左右子树
- 106 从中序和后序遍历构造二叉树
  - 核心：基于后序/前序序列可以确定D，随后在中序序列中确定D的位置，进一步确定左右子树的节点个数随后反推其在前序/后序序列的子树的节点区间
- 654 最大二叉树
  - 核心：基于递归方式构建二叉树，每次选择区间内的最大值作为D进行构建，随后根据子树的节点区间递归构建左、右子树
- 617 合并二叉树
  - BFS：基于3个队列辅助遍历，mergeQueue用于辅助处理合并后的节点，每次遍历从队列中取出节点，根据两树各自的左右子节点的null校验处理合并节点
  - DFS（推荐）：构建mergerHelper(TreeNode node1,TreeNode2)辅助合并后的二叉树构建，根据两树各自的左右子节点的null校验处理合并节点
    - ① node1==null && node2==null => null
    - ② node1、node2中其中一个为null =>返回不为null的那个节点
    - ③ node1!=null && node2!=null => 需处理合并
      - 创建根节点（合并）
      - 递归构建左右子节点
      - 返回根节点
二叉搜索树的属性：二叉搜索树的中序遍历得到的序列是有序序列（对于二叉搜索树的题型的相关遍历要充分利用该特性，优化代码实现）
- 700 二叉搜索树中的搜索
  - 通用搜索：可以基于BFS、DFS的方式进行检索，适用于所有类型的二叉树
  - 特性搜索：基于迭代、递归DFS的方式进行检索，利用二叉树特性进行缩圈（通过校验当前遍历节点值与目标值来选择遍历方向）
- 098 验证二叉搜索树
  - 模拟法：二叉搜索树的中序遍历序列是升序序列，因此可以将其转化为两步（① 获取LDR序列 ② 验证LDR序列是否为递增序列）
  - 空间优化：基于上述模拟法思路，实际上可以直接在遍历的过程中直接进行校验preNode与curNode的值关系，校验是否始终满足preNodeVal<curNodeVal进而达到优化空间效率的目的
    - DFS：可以基于中序遍历的递归方式，在递归的过程中校验preNode与curNode
- 530 二叉搜索树的最小绝对差
  - 思路：求二叉搜索树中两个节点的最小绝对值差，转化为求中序序列中相邻两数的最小差值的绝对值
  - 遍历法：同理，基于递归（LDR）的思路，求preNode与curNode的最小差值
- 501 二叉搜索树中的众数（可能存在1个或多个众数）
  - 模拟法：遍历统计各个元素的出现频次封装为map，随后遍历map获取最大频次并封装可能出现的多个众数
    - 思路1：在封装map的过程就记录maxCnt ，当满足map.get(key)==maxCnt的key即为众数
    - 思路2：遍历map，记录目前的maxCnt，如果发现出现新的最大频次则需更新maxCnt并清空当前的众数集合，如果是相等则说明截至目前遍历为止出现频次相同的可能的众数（加入结果集），如果遍历频次小于maxCnt则不需做处理（这个思路在空间优化版本中是一个重要的核心）
  - 空间优化：所谓空间优化版本实际上就是不用map记录整个元素出现频次的映射关系，而是通过滚动变量来处理，递归处理过程主要分为两步（① 更新当前遍历元素的出现频次 ② 更新最大出现频次）
    - 涉及滚动变量：curNodeVal（当前遍历节点值）、curNodeCnt（当前遍历节点出现频次）、maxCnt（目前的元素出现最大频次/即目前选择的众数的出现频次）、res(List)（众数结果集）
    - 实现细节（update()核心）：LDR中序遍历的递归方式
      - ① 更新当前遍历元素出现频次：
        如果curNodeVal==node.val说明出现连续重复，频次累加
        如果curNodeVal!=node.val说明出现新元素，更新（重置）当前遍历节点映射（curNodeVal=node.val、curNodeCnt=1）
      - ② 更新最大出现频次（校验curNodeCnt与maxCnt的关系）
        curNodeCnt < maxCnt：无处理
        curNodeCnt = maxCnt：出现了【出现频次相同的元素】，纳入目前的众数结果集
        curNodeCnt > maxCnt：出现了【出现频次更高的元素】，需更新maxCnt（maxCnt=curNodeCnt）并重置res（先 clean 集合，后 add curNodeVal）
- 538 把二叉搜索树转化为累加树
二叉树公共祖先问题：
- 236 二叉树的最近公共祖先
  - 分类讨论：递归检索，判断node与p、q的关系
    - ① node为null（空节点）、p、q中的任一个，直接返回node
    - ② node为其他情况，则需递归从其子树的检索结果中分情况讨论（findLeft（递归左子树）、findRight（递归右子树））
      - findLeft、findRight均为null 说明左右子树都没找到公共节点，返回null
      - findLeft、findRight均不为null 说明左右子树都找到了公共节点，则当前节点即为公共节点，返回node
      - findLeft、findRight 中只有一个为null，则公共节点在不为null的子树中，返回不为null的那个分支（return findLeft==null?findRight:findLeft）
- 235 二叉搜索树的最近公共祖先
  - 通用法：参考【236】的思路，可实现通用检索二叉树的最近公共祖先
  - 特性法：需结合二叉搜索树的特性进行检索，将题目转化为求第1个落在p、q节点限定区间（[pVal,qVal]或[qVal,pVal]）的节点，那么就可以借助迭代或者递归的方式进行检索
二叉搜索树的修改与构造：
- 701 二叉搜索树中的插入操作
  - 模拟法：【LDR=>插入数据=>转化为树】
    - ① LDR遍历获取集合
    - ②insertByBinary 基于二分检索查找下一个可插入位置并执行插入操作
    - ③ buildHelper 将插入更新后的列表集合转化为二叉搜索树
  - 遍历法：基于迭代或递归的思路，寻找到可插入位置
    - ① 迭代思路：比较当前遍历节点nodeVal与插入目标值target的关系
      - 如果target<nodeVal需插入左边（则进一步判断当前遍历节点是否存在左节点，不存在则直接插入，存在则继续向左遍历寻找）
      - 如果target>nodeVal需插入右边（则进一步判断当前遍历节点是否存在右节点，不存在则直接插入，存在则继续向右遍历寻找）
    - ② 递归思路：转化为递归遍历思路
- 450 删除二叉搜索树中的节点
  - 重构法❌：【LDR=>删除数据=>转化为树】（这种需要重构树的思路可能会破坏原有的树结构，不完全适配）
  - 模拟法：删除节点和核心思路在于寻找待删除节点，重新链接节点关系（在这个过程中涉及到节点的链接更新，因此需要在遍历的过程中记录待删除目标节点的前置节点preNode）
    - ① 寻找待删除节点target，如果target存在则继续下面的步骤，如果不存在则不需要执行删除操作（返回root）
    - ② target删除后需要重新构建其原来的左、右节点（leftNode、rightNode）的关系，得到一棵新的子树（newSubRoot）,因此要思考newSubRoot的不同情况
      - leftNode、rightNode均为null，说明删除的是叶子节点，那么得到的新的子树实际上是一个空树，即newSubRoot指向null
      - leftNode、rightNode中只有1个不为null，说明只有不为null的那个节点才能上位构建新的子树，即newSubRoot==(leftNode==null?rightNode:leftNode)
      - leftNode、rightNode均不为null，则需要将原来的leftNode挂靠在rightNode的最左端，更新后的rightNode上位成为newSubRoot
    - ③ 更新preNode与newSubRoot的关系，即将newSubRoot挂载到原来断开的位置
      - preNode==null：说明待删除节点为root（根节点没有前置节点），那么newSubRoot即为删除根节点后的内容
      - preNode!=null：判断key(待删除元素)与preNodeVal的关系，看需要将其挂载到左侧还是右侧，构建preNode与newSubRoot的父子关系
- 669 修剪二叉搜索树
  - 模拟法：需要将二叉检索树的值限定在[low,high]且不改变原来的树结构
    - ① 寻找第1个落在[low,high]区间的节点target
    - ② 从target位置开始继续遍历左、右子树进行裁剪
      - 遍历左子树：当前遍历节点（leftP）的左子树节点不为null的情况下进行校验（左子树只需要校验low边界，因为左子树的所有节点均小于curVal，且curVal在步骤①中已经明确落在[low,high]区间）
        如果其左子节点越界（小于low）则需要进行裁剪，让其左子节点的右子节点覆盖左子节点leftP.left = leftP.left.right（相当于挑一个更大的孙子节点上位，等待下一步校验）
        如果其左子节点在限定范围（大于等于low）则继续往左校验：leftP = leftP.left
      - 遍历右子树：同理，右子树只需要关注high边界校验
        如果其右子节点越界（大于high）则需要进行裁剪，让其右子节点的左子节点覆盖右子节点rightP.right= rightP.right.left（相当于挑一个更小的孙子节点上位，等待下一步校验）
        如果其右子节点在限定范围（小于等于high）则继续往右校验：rightP= rightP.right
    - ③ 最终返回裁剪后的target
- 108 将有序数组转化为二叉搜索树
  - 递归法：基于buidHelper(int[] nums,int start,int end)进行递归构建，每次选择限定范围内的中点位置构建节点，然后递归构建左、右子树

（3）递归算法三要素

【1】确定递归函数的参数和返回值：确定哪些参数是递归过程中需要处理的，在递归函数中加上参数，并确定递归返回值类型

【2】确定终止条件：写递归算法的时候经常会遇到栈溢出的错误（主要是递归的终止条件设定错误导致），操作系统是用栈结构保存每一层递归的信息，如果递归没有终止，则操作系统的内存栈则必然溢出

【3】确定单层递归的逻辑：每一层递归需要处理的信息（递归的核心是重复调用自己来实现递归过程）

常见模板定义（todo res、path 基础版本和框架）

常见题型

🍚01-二叉树的遍历

🚀层序遍历（广度优先遍历）

（1）层序遍历基础

普通层序遍历：返回遍历序列

// 层序遍历：分层遍历（辅助队列实现）
public List<Integer> levelOrder(TreeNode root){
    // root为null判断
    if(root==null){
        return new ArrayList<>();
    }

    // 定义遍历结果集
    List<Integer> res= new ArrayList<>();

    // 构建辅助队列进行遍历
    Deque<TreeNode> queue = new LinkedList<>(); // 要使用队列的方法，此处用Deque接收
    queue.offer(root); // 初始化队列
    // 遍历队列元素
    while(!queue.isEmpty()){
        // 取出当前队列元素
        TreeNode cur = queue.poll();
        res.add(cur.val);

        // 如果当前节点存在左右节点，则分别入队
        if(cur.left!=null){
            queue.offer(cur.left);
        }
        if(cur.right!=null){
            queue.offer(cur.right);
        }
    }
    return res;
}

分层层序遍历：分层遍历

分层遍历的核心思路实际是在上述普通遍历的基础上划分层次，每次遍历的时候先记录当前队列元素个数（一层），然后遍历当层内容，随后进入下一层的遍历，直到队列中所有元素都遍历完成

// 层序遍历：分层遍历（辅助队列实现）
public List<List<Integer>> levelOrder(TreeNode root) {
    // root为null判断
    if (root == null) {
        return new ArrayList<>();
    }

    // 定义遍历结果集
    List<List<Integer>> res = new ArrayList<>();

    // 构建辅助队列进行遍历
    Deque<TreeNode> queue = new LinkedList<>(); // 要使用队列的方法，此处用Deque接收
    queue.offer(root); // 初始化队列
    // 遍历队列元素
    while (!queue.isEmpty()) {
        // 定义当层序列
        List<Integer> curList = new LinkedList<>();
        // 记录当前队列元素个数（当层元素个数）
        int queueSize = queue.size();
        // 分层进行遍历
        for (int i = 0; i < queueSize; i++) {
            // 取出当前队列元素
            TreeNode cur = queue.poll();
            // 记录元素值
            curList.add(cur.val);

            // 如果当前节点存在左右节点，则分别入队
            if (cur.left != null) {
                queue.offer(cur.left);
            }
            if (cur.right != null) {
                queue.offer(cur.right);
            }
        }
        // 当层遍历完成，封装结果集，随后进入下一层遍历
        res.add(curList);
    }
    return res;
}

（2）层序遍历关联题型

掌握了层序遍历核心，那么对于层序遍历的关联题型则可灵活应用，主要扩展下述题型

🟡102 二叉树的层序遍历open in new window

给你二叉树的根节点 root ，返回其节点值的 层序遍历 。（即逐层地，从左到右访问所有节点）。

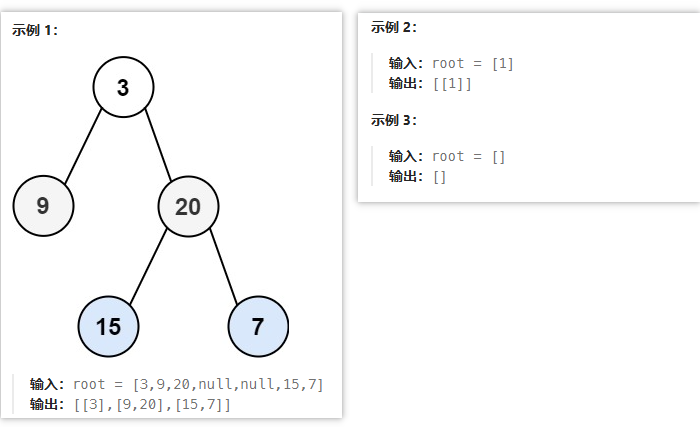
思路核心：可以将最原始的层序遍历先框下来，然后基于其进行分层改造，这样思路可能会更清晰一点

public List<List<Integer>> levelOrder(TreeNode root) {
    if (root == null) {
        return new ArrayList<>();
    }

    // 结果集定义
    List<List<Integer>> res = new ArrayList<>();

    // 构建辅助队列
    Deque<TreeNode> queue = new LinkedList<>();
    queue.offer(root); // 初始化
    // 遍历队列
    while (!queue.isEmpty()) {
        // 遍历当层元素
        List<Integer> curList = new ArrayList<>();
        int curSize = queue.size();

        for (int i = 0; i < curSize; i++) {
            // 取出元素
            TreeNode cur = queue.poll();
            curList.add(cur.val);
            // 左右节点如果存在则分别入队
            if (cur.left != null) {
                queue.offer(cur.left);
            }
            if (cur.right != null) {
                queue.offer(cur.right);
            }
        }

        // 当层元素遍历完成，载入结果集
        res.add(curList);
    }

    // 返回结果集
    return res;
}

复杂度分析：

时间复杂度：O（n）需遍历所有树节点
空间复杂度：O（n）需借助辅助队列存储树节点（最坏的情况下有两层：第1层1个节点，第2层n-1个节点）

🟡 103 二叉树的锯齿形层序遍历open in new window

给你二叉树的根节点 root ，返回其节点值的 锯齿形层序遍历 。（即先从左往右，再从右往左进行下一层遍历，以此类推，层与层之间交替进行）。

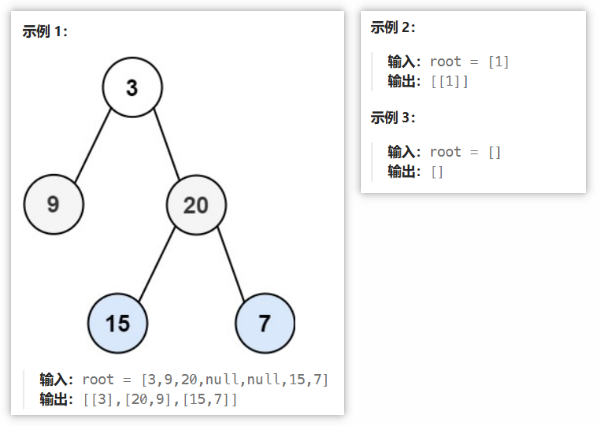
核心思路：基于层序遍历思路，分层遍历元素，每遍历一层元素就更新遍历方向。在载入curList每一层的元素的时候根据当前遍历方向来选择元素加入的顺序（正序尾插、逆序头插），正常载入结果集即可

/**
 * 🟡 103 二叉树的锯齿形层序遍历 - https://leetcode.cn/problems/binary-tree-zigzag-level-order-traversal/description/
 */
public class Solution1 {

    /**
     * 锯齿形层序遍历：先从左往右、后从右往左
     * - 此处遍历顺序的处理在载入当层元素集合的时候处理（正序尾插、逆序头插）
     */
    public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
        if (root == null) {
            return new ArrayList<>();
        }

        List<List<Integer>> res = new ArrayList<>(); // 定义结果集

        // 定义遍历方向
        boolean leftToRight = true; // 初始化从左往右的方向进行遍历

        // 构建辅助队列进行遍历
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            int curSize = queue.size(); // 当层元素个数
            List<Integer> curList = new ArrayList<>(); // 记录当层元素
            for (int i = 0; i < curSize; i++) {
                // 取出节点，按照指定方向进行遍历
                TreeNode node = queue.poll();

                // 根据遍历方向决定顺序
                if (leftToRight) {
                    // 从左到右遍历
                    curList.add(node.val);
                } else {
                    // 从右到左遍历（头插）
                    curList.add(0, node.val);
                }

                // 子节点入队
                if (node.left != null) {
                    queue.offer(node.left);
                }
                if (node.right != null) {
                    queue.offer(node.right);
                }
            }

            // 载入结果集
            res.add(curList);

            // 当层遍历完成，改变遍历方向
            leftToRight = !leftToRight;

        }

        // 返回遍历结果
        return res;
    }

}

🟡107 二叉树的层次遍历IIopen in new window

给你二叉树的根节点 root ，返回其节点值 自底向上的层序遍历 。（即按从叶子节点所在层到根节点所在的层，逐层从左向右遍历）

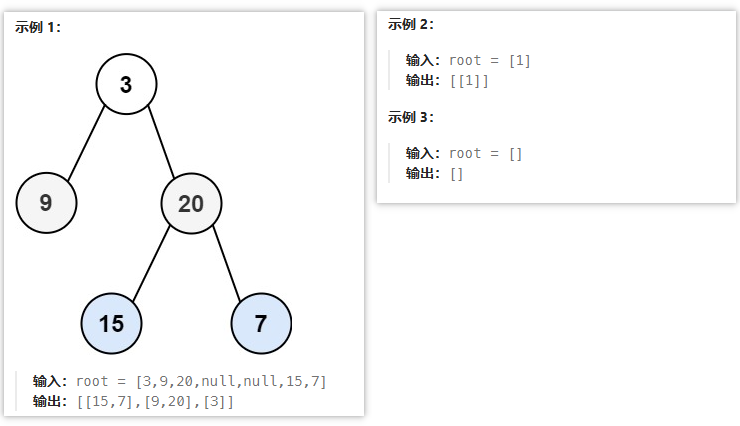
核心思路：
- （1）层序遍历+头插：每遍历一层拿到遍历序列，将其头插到res的头部
  - res.addFirst(curList);、res.add(0,curList);
- （2）层序遍历+反转：正常构建层序遍历，将最终的res反转即可得到"自底向上从左到右"的遍历序列
  - Collections.reverse(res)
- （3）层序遍历+逆序输出：正常构建层序遍历，将层序遍历的结果集逆序遍历输出

/**
 * 107 二叉树的层序遍历II
 */
public class Solution1 {

    /**
     * - （1）层序遍历+头插：每遍历一层拿到遍历序列，将其头插到`res`的头部
     * - （2）层序遍历+反转：正常构建层序遍历，将最终的`res`反转即可得到"自底向上 从左到右"的遍历序列
     */
    public List<List<Integer>> levelOrderBottom(TreeNode root) {
        if (root == null) {
            return new ArrayList<>();
        }

        // 结果集定义
        List<List<Integer>> res = new ArrayList<>();

        // 构建辅助队列
        Deque<TreeNode> queue = new LinkedList<>();
        queue.offer(root); // 初始化
        // 遍历队列
        while (!queue.isEmpty()) {
            // 遍历当层元素
            List<Integer> curList = new ArrayList<>();
            int curSize = queue.size();

            for (int i = 0; i < curSize; i++) {
                // 取出元素
                TreeNode cur = queue.poll();
                curList.add(cur.val);
                // 左右节点如果存在则分别入队
                if (cur.left != null) {
                    queue.offer(cur.left);
                }
                if (cur.right != null) {
                    queue.offer(cur.right);
                }
            }

            // 当层元素遍历完成，载入结果集
            // res.add(curList);
            res.add(0,curList); // 方案1：在指定位置插入结果集
        }

        // 返回结果集
        return res;
    }
}

/**
 * 107 二叉树的层序遍历II
 */
public class Solution2 {

    /**
     * - （1）层序遍历+头插：每遍历一层拿到遍历序列，将其头插到`res`的头部
     * - （2）层序遍历+反转：正常构建层序遍历，将最终的`res`反转即可得到"自底向上 从左到右"的遍历序列
     */
    public List<List<Integer>> levelOrderBottom(TreeNode root) {
        if (root == null) {
            return new ArrayList<>();
        }

        // 结果集定义
        List<List<Integer>> res = new ArrayList<>();

        // 构建辅助队列
        Deque<TreeNode> queue = new LinkedList<>();
        queue.offer(root); // 初始化
        // 遍历队列
        while (!queue.isEmpty()) {
            // 遍历当层元素
            List<Integer> curList = new ArrayList<>();
            int curSize = queue.size();

            for (int i = 0; i < curSize; i++) {
                // 取出元素
                TreeNode cur = queue.poll();
                curList.add(cur.val);
                // 左右节点如果存在则分别入队
                if (cur.left != null) {
                    queue.offer(cur.left);
                }
                if (cur.right != null) {
                    queue.offer(cur.right);
                }
            }

            // 当层元素遍历完成，载入结果集
             res.add(curList);
        }

        // 方案2：反转结果集
        Collections.reverse(res);

        // 返回结果集
        return res;
    }

}

复杂度分析：
- 时间复杂度：O（n）需遍历所有树节点
- 空间复杂度：O（n）需借助辅助队列存储树节点（最坏的情况下有两层：第1层1个节点，第2层n-1个节点）
  - 如果是采用【头插】思路，则只需要辅助队列空间占用
  - 如果是采用【反转结果集】思路，则需考虑借助工具方法进行反转可能会涉及到额外的空间占用
  - 如果是采用【逆序遍历】封装思路，还需考虑逆序遍历的实现复杂度和封装新结果集的空间复杂度

🟡 199 二叉树的右视图open in new window

给定一个二叉树的 根节点 root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

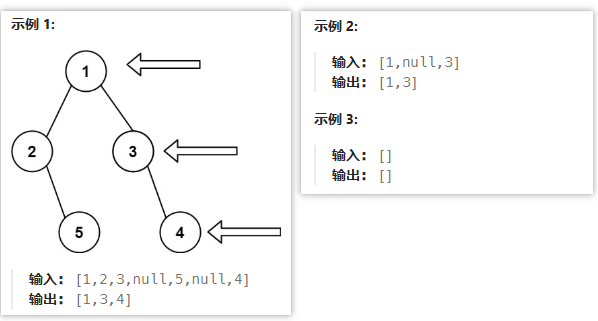
思路分析：将"右视图"的概念转化为求二叉树每一层的最右侧节点构成的结果集

/**
 * 199 二叉树的右视图
 */
public class Solution1 {

    // 思路：返回每一层的最右侧节点
    public List<Integer> rightSideView(TreeNode root) {
        if(root==null){
            return new ArrayList<>();
        }

        // 定义结果集
        List<Integer> res = new ArrayList<>();

        // 定义辅助队列
        Deque<TreeNode> queue = new LinkedList<>();
        queue.offer(root); // 初始化

        // 遍历队列
        while(!queue.isEmpty()){
            // 分层遍历
            int curSize = queue.size();
            for(int i=0;i<curSize;i++){
                // 取出元素
                TreeNode cur = queue.poll();
                // 判断当层遍历索引是否为最后一个
                if(i==curSize-1){
                    res.add(cur.val); // 如果是当层最后一个则加入结果集
                }

                // 如果存在左右节点，分别入队
                if(cur.left!=null){
                    queue.offer(cur.left);
                }
                if(cur.right!=null){
                    queue.offer(cur.right);
                }
            }
        }

        // 返回结果
        return res;
    }
}

复杂度分析：
- 时间复杂度：O（n）需遍历所有树节点
- 空间复杂度：O（n）需借助辅助队列存储树节点（最坏的情况下有两层：第1层1个节点，第2层n-1个节点）

🟢 637 二叉树的层平均值open in new window

给定一个非空二叉树的根节点 root , 以数组的形式返回每一层节点的平均值。与实际答案相差 10-5 以内的答案可以被接受。

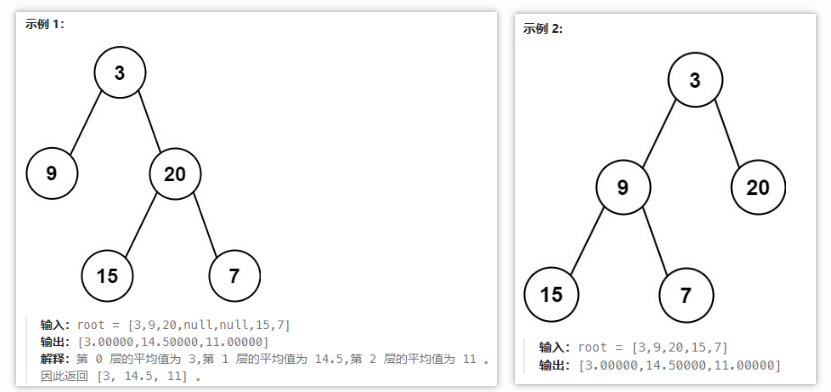
核心思路：基于层序遍历思路，分层统计层平均值（注意数值类型定义和小数点处理问题）

/**
 * 637 二叉树的层平均值
 */
public class Solution1 {

    // 思路：分层统计记录
    public List<Double> averageOfLevels(TreeNode root) {
        if (root == null) {
            return new ArrayList<>();
        }

        // 定义结果集
        List<Double> res = new ArrayList<>();

        // 定义辅助队列
        Deque<TreeNode> queue = new LinkedList<>();
        queue.offer(root); // 初始化

        // 遍历队列
        while (!queue.isEmpty()) {
            // 分层遍历
            int curSize = queue.size();
            // int curSum = 0; // 初始化当层结果累计
            Double curSum = 0.00; // 初始化当层结果累计
            for (int i = 0; i < curSize; i++) {
                // 取出元素
                TreeNode cur = queue.poll();
                curSum += cur.val;

                // 如果存在左右节点，分别入队
                if (cur.left != null) {
                    queue.offer(cur.left);
                }
                if (cur.right != null) {
                    queue.offer(cur.right);
                }
            }
            // 当层遍历结束，计算平均值
            // res.add( curSum / 1.0 / curSize);
            res.add(curSum / curSize);
        }

        // 返回结果
        return res;
    }
}

复杂度分析：
- 时间复杂度：O（n）需遍历所有树节点
- 空间复杂度：O（n）需借助辅助队列存储树节点（最坏的情况下有两层：第1层1个节点，第2层n-1个节点），还需额外的常数级空间累计当层节点之和

🟡 429 N叉树的层序遍历open in new window

给定一个 N 叉树，返回其节点值的层序遍历。（即从左到右，逐层遍历）。

树的序列化输入是用层序遍历，每组子节点都由 null 值分隔（参见示例）。

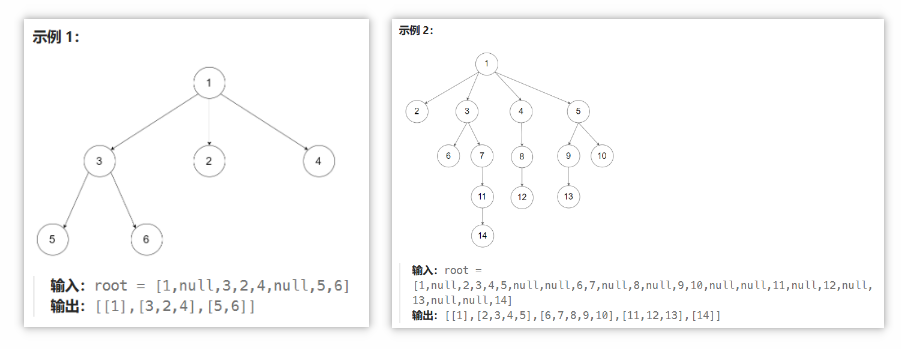
核心思路：对比普通的分层层序遍历，此处主要在于对多个孩子节点的处理（原二叉树是2个节点，现多叉树是多个孩子节点，一一进行判断即可）

/**
 * 429 N 叉树的遍历
 */
public class Solution1 {

    public List<List<Integer>> levelOrder(NTreeNode root) {
        // 判断root是否为null
        if (root == null) {
            return new ArrayList<>();
        }

        // 定义遍历结果集
        List<List<Integer>> res = new ArrayList<>();

        // 构建辅助队列
        Deque<NTreeNode> queue = new LinkedList<>();
        queue.offer(root); // 初始化队列

        // 遍历队列元素
        while (!queue.isEmpty()) {
            // 遍历当层元素
            List<Integer> curList = new ArrayList<>();
            // 记录当层元素个数
            int curSize = queue.size();
            // 分层遍历
            for(int i=0;i<curSize;i++){
                // 取出队列元素
                NTreeNode cur = queue.poll();
                curList.add(cur.val);

                // 如果子节点不为空则入队
                List<NTreeNode> children = cur.children;
                queue.addAll(children); // 子节点添加可以用工具方法替代，无需额外手动遍历
                /*
                if(!children.isEmpty()){
                    for (NTreeNode child : children){
                        if(child!=null){
                            queue.offer(child);
                        }
                    }
                }
                */
            }
            // 当层遍历完成，封装结果集
            res.add(curList);
        }

        // 返回响应结果
        return res;
    }

}

复杂度分析：
- 时间复杂度：O（n）需遍历所有树节点
- 空间复杂度：O（n）需借助辅助队列存储树节点（最坏的情况下有两层：第1层1个节点，第2层n-1个节点）

🟡 515 在每个树行中找最大值open in new window

给定一棵二叉树的根节点 root ，请找出该二叉树中每一层的最大值。

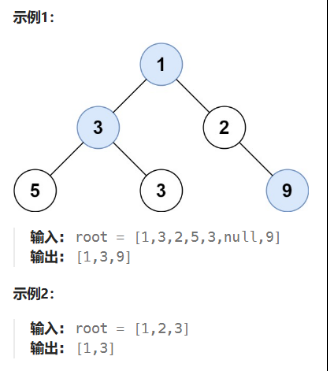
==核心思路：==分层遍历，求当层最大值

/**
 * 515 在每个树行中最大值
 */
public class Solution1 {

    // 思路：基于分层遍历，记录行最大值，当层遍历结束封装结果集
    public List<Integer> largestValues(TreeNode root) {
        // root 为null处理
        if (root == null) {
            return new ArrayList<>();
        }
        // 定义结果集
        List<Integer> res = new ArrayList<>();

        // 构建辅助队列
        Deque<TreeNode> queue = new LinkedList<>();
        queue.offer(root); // 初始化队列

        // 遍历队列
        while (!queue.isEmpty()) {
            // 分层遍历
            int curSize = queue.size();
            int curMax = Integer.MIN_VALUE; // 记录当层最大值

            // 遍历当层节点
            for (int i = 0; i < curSize; i++) {
                // 获取遍历节点
                TreeNode cur = queue.poll();

                // 更新最大值
                curMax = Math.max(curMax, cur.val);

                // 判断是否存在左右节点，存在则分别入队
                if (cur.left != null) {
                    queue.offer(cur.left);
                }
                if (cur.right != null) {
                    queue.offer(cur.right);
                }
            }

            // 当层遍历结束，记录结果
            res.add(curMax);
        }

        // 返回结果集
        return res;
    }
}

复杂度分析：

时间复杂度：O（n）需遍历所有树节点
空间复杂度：O（n）需借助辅助队列存储树节点（最坏的情况下有两层：第1层1个节点，第2层n-1个节点）

基于深度优先遍历的思路

用树的「先序遍历」来进行「深度优先搜索」处理，并用 curHeight 来标记遍历到的当前节点的高度。当遍历到 curHeight 高度的节点就判断是否更新该层节点的最大值

// 基于深度优先遍历的思路（dfs）
class Solution {
    public List<Integer> largestValues(TreeNode root) {
        if (root == null) {
            return new ArrayList<Integer>();
        }
        List<Integer> res = new ArrayList<Integer>();
        dfs(res, root, 0);
        return res;
    }

    public void dfs(List<Integer> res, TreeNode root, int curHeight) {
        if (curHeight == res.size()) {
            res.add(root.val);
        } else {
            res.set(curHeight, Math.max(res.get(curHeight), root.val));
        }
        if (root.left != null) {
            dfs(res, root.left, curHeight + 1);
        }
        if (root.right != null) {
            dfs(res, root.right, curHeight + 1);
        }
    }
}

复杂度分析
- 时间复杂度：O(n)，其中 n 为二叉树节点个数。二叉树的遍历中每个节点会被访问一次且只会被访问一次
- 空间复杂度：O(height)。其中 height 表示二叉树的高度。递归函数需要栈空间，而栈空间取决于递归的深度，因此空间复杂度等价于二叉树的高度

🟡 116 填充每个节点的下一个右侧节点指针open in new window

给定一个 完美二叉树 ，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下：

struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。

初始状态下，所有 next 指针都被设置为 NULL。

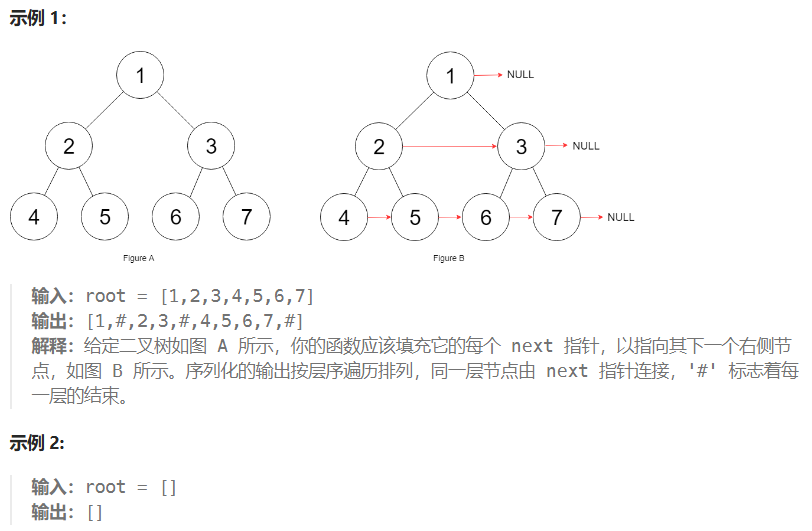
解法1：层序遍历
从上到下、从左到右（传统层次遍历）：cur.next指向当层遍历的下一个节点（cur不为当层最后一个节点时封装next，从队列中取即可）
从上到下、从右到左：cur.next指向当层遍历的上一个节点（每遍历一个节点，记录当前节点为nextNode，作为下一个遍历节点的next指向）

核心思路：这个题目的思路最基础的解决方式就是采用层次遍历从上到下，从右到左进行遍历，和【117 填充每个节点的下一个右侧节点指针II】是一样的解法

/**
 * 116 填充每个节点的下一个右侧节点指针
 */
public class Solution1 {

    // 思路：封装每个节点的next指针
    public Node connect(Node root) {
        // 判断root为null的情况
        if(root==null){
            return null;
        }

        // 构建辅助队列
        Deque<Node> queue = new LinkedList<>();
        queue.offer(root); // 初始化队列

        // 遍历队列节点(层序遍历顺序：从上到下、从右到左)
        while(!queue.isEmpty()){
            // 分层遍历
            int curSize = queue.size();
            // 定义nextNode初始化为null（对于每一层都右一个初始化的nextNode节点）
            Node nextNode = null;
            for(int i=0;i<curSize;i++){
                Node cur = queue.poll();
                cur.next = nextNode; // 更新当前节点的nextNode

                // 如果存在子节点则入队（遍历顺序从右往左，因此入队顺序从右往左）
                if(cur.right !=null){
                    queue.add(cur.right);
                }
                if(cur.left !=null){
                    queue.add(cur.left);
                }

                // 当前节点遍历完成，更新nextNode（用于下个节点的next指向）
                nextNode = cur;
            }
        }

        // 返回节点
        return root;
    }
}


class Node {
    public int val;
    public Node left;
    public Node right;
    public Node next;
}

复杂度分析：

时间复杂度：O（n）需遍历所有树节点
空间复杂度：O（n）需借助辅助队列存储树节点（最坏的情况下有两层：第1层1个节点，第2层n-1个节点）

解法2：技巧法（常数级空间复杂度）
递归方式实现，充分利用完美二叉树的特性：相当于遍历每个节点，然后分别处理它的左、右子节点的next指针
递归出口：如果node.left为null则结束（对于完美二叉树而言，除了叶子结点所有父节点都有两个子节点，因此如果左子节点为空则无需继续递归）
递归过程：
node.left节点的next指针指向node.right
node.right节点的next指针指向node.next.left（如果node.next存在的前提下）
继续递归node.left、node.right

/**
 * 116 填充每个节点的下一个右侧节点指针
 * 完美二叉树
 */
public class Solution2 {

    public Node connect(Node root) {
        // 判断root为null的情况
        if (root == null) {
            return null;
        }
        // 递归封装next
        connectNext(root);
        return root;
    }

    public void connectNext(Node node) {
        /**
         * 递归出口：如果node.left为null则结束
         * 对于完美二叉树而言，除了叶子结点所有父节点都有两个子节点，因此如果左子节点为空则无需继续递归
         */
        if (node.left == null) {
            return;
        }

        // 递归过程（分别设置当前节点的左子节点、右子节点的next指针）
        node.left.next = node.right; // 设置左子节点的next指针

        // 如果node.next存在则设置右子节点的next指针
        if (node.next != null) {
            node.right.next = node.next.left;
        }

        // 对节点的左右子节点分别进行递归
        connectNext(node.left);
        connectNext(node.right);
    }
}

中规中矩递归处理：处理左、右子节点

/**
 * 🟡 116 填充每个节点的下一个指针
 */
public class Solution116_03 {

    /**
     * DFS 思路：递归处理当前节点的左右子节点的next指针
     */
    public Node connect(Node root) {
        dfs(root);
        return root;
    }

    public void dfs(Node node) {
        // 递归出口
        if (node == null) {
            return;
        }

        // 分别处理左、右节点的next指针
        if (node.left != null) {
            node.left.next = node.right; // 当前节点的左节点的next指针指向node.right
        }
        if (node.right != null) {
            if (node.next != null) { // 需要处理右节点的next指针的情况，看node.next是否存在，如果不存在也不需要处理
                node.right.next = node.next.left; // 当前节点的右节点的next指着指向node.next.left
            }
        }

        // 递归处理
        dfs(node.left);
        dfs(node.right);
    }
}

🟡 117 填充每个节点的下一个右侧节点指针IIopen in new window

基于层序遍历BFS的思路，是通用的做法，可以同时解决116、117的问题，不限定二叉树类型

给定一个二叉树：

struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL 。

初始状态下，所有 next 指针都被设置为 NULL

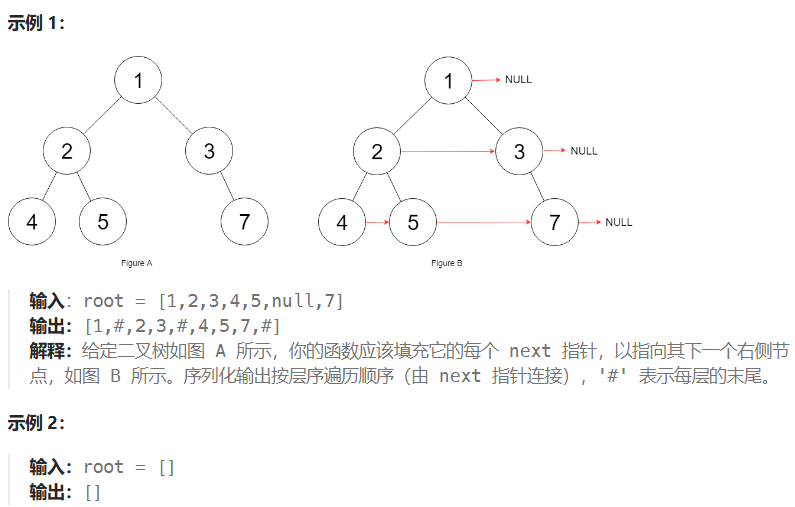
核心思路：分层遍历，主要处理每一层节点的的next指针（如果存在，则指向其下一个节点，如果不存在则指向null）

硬核思路是分层遍历封装所有元素，然后再遍历一遍封装好的结果集，如果存在next，则指向其下一个节点，如果不存在则指向null

（1）此处的问题核心在于想要封装next就得先得到"下一个节点"，如果通过原有的层次遍历思路，队列中存储的是当层的元素，因此可以在分层遍历的过程中先拿到cur，然后再读取下一个节点（peek()读取）的值（存在则读取，不存在说明next为null）cur.next指向当层遍历的下一个节点（从上到下，从左到右）

（2）另一种方案可以考虑将每一层的入队顺序反着来，这样当遍历到这个元素的时候就能够先把下个节点的next初始化，然后遍历下个节点的时候就可以进行指向了。因为此处只需要封装每个节点的next指针，因此只需要关注遍历、设置next即可（关注核心，不要跑偏方向纠结输出）cur.next指向当层遍历的上一个节点（从上到下，从右到左）

/**
 * 117 填充每个节点的下一个右侧节点指针II 
 * 层序遍历：从上到下、从右到左，对于每一层的元素节点遍历，当前遍历的节点会作为下一个遍历的节点的`next`
 */
public class Solution1 {

    // 思路：封装每个节点的next指针
    public Node connect(Node root) {
        // 判断root为null的情况
        if(root==null){
            return null;
        }

        // 构建辅助队列
        Deque<Node> queue = new LinkedList<>();
        queue.offer(root); // 初始化队列

        // 遍历队列节点(层序遍历顺序：从上到下、从右到左)
        while(!queue.isEmpty()){
            // 分层遍历
            int curSize = queue.size();
            // 定义nextNode初始化为null（对于每一层都右一个初始化的nextNode节点）
            Node nextNode = null;
            for(int i=0;i<curSize;i++){
                Node cur = queue.poll();
                cur.next = nextNode; // 更新当前节点的nextNode

                // 如果存在子节点则入队（遍历顺序从右往左，因此入队顺序从右往左）
                if(cur.right !=null){
                    queue.add(cur.right);
                }
                if(cur.left !=null){
                    queue.add(cur.left);
                }

                // 当前节点遍历完成，更新nextNode（用于下个节点的next指向）
                nextNode = cur;
            }
        }

        // 返回节点
        return root;
    }
}

复杂度分析：

时间复杂度：O（n）需遍历所有树节点
空间复杂度：O（n）需借助辅助队列存储树节点（最坏的情况下有两层：第1层1个节点，第2层n-1个节点）

🟢 104 二叉树的最大深度open in new window

给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

==核心思路：==统计二叉树层数，可以基于两种思路
- 层序遍历 BFS：分层遍历，统计层数
- 后序遍历 DFS：将求当前节点的最大深度转化为求其左、右子树的最大深度 +1（max{ maxDepth(node.left),maxDepth(node.right) } + 1 即为左右子树的最大深度+当前节点（1层））

层序遍历

/**
 * 104 二叉树的最大深度
 */
public class Solution1 {
    // 层序遍历：迭代法
    public int maxDepth(TreeNode root) {
        // 判断root为null的情况
        if (root == null) {
            return 0;
        }

        // 定义层数（最大深度）
        int level = 0;

        // 构建辅助队列
        Deque<TreeNode> queue = new LinkedList<>();
        queue.offer(root); // 初始化队列

        // 分层遍历队列，统计层数
        while (!queue.isEmpty()) {
            // 分层统计
            int curSize = queue.size();
            for (int i = 0; i < curSize; i++) {
                TreeNode cur = queue.poll();
                // 如果左右子节点不为空，分别入队
                if (cur.left != null) {
                    queue.offer(cur.left);
                }
                if (cur.right != null) {
                    queue.offer(cur.right);
                }
            }
            // 当层遍历结束，记录层数
            level++;
        }
        // 遍历层数即为二叉树的最大深度
        return level;
    }
}

后序遍历 DFS

/**
 * 104 二叉树的最大深度
 */
public class Solution2 {
    /**
     * 递归法 DFS 思路：
     * 节点的最大深度：max{ maxDepth(node.left),maxDepth(node.right) } + 1 即为左右子树的最大深度+当前节点（1层）
     */
    public int maxDepth(TreeNode root) {
        // 递归出口
        if (root == null) {
            return 0;
        }
        // 递归过程：计算左右子节点的最大深度
        int left = maxDepth(root.left);
        int right = maxDepth(root.right);
        // 获取当前子树的最大深度
        return Math.max(left, right) + 1;
    }
}

扩展题型：N 叉树的最大深度open in new window

层序遍历
DFS 递归

/**
 * 559 N 叉树的最大深度
 */
public class Solution1 {

    public int maxDepth(Node root) {
        // 递归出口
        if (root == null) {
            return 0;
        }
        // 计算子节点的最大深度
        List<Node> children = root.children;
        int max = 0;
        for (Node node : children) {
            max = Math.max(max, maxDepth(node));
        }
        return max + 1;
    }

}

class Node {
    public int val;
    public List<Node> children;

    public Node() {
    }

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val, List<Node> _children) {
        val = _val;
        children = _children;
    }
};

🟢 111 二叉树的最小深度open in new window

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

**说明：**叶子节点是指没有子节点的节点。

核心思路：

（1）层序遍历：按照遍历每一层的元素，如果遍历到当层的叶子结点（节点无左右节点）直接返回depth
- 可以理解为基于层序遍历，从上到下、从左到右、找到第一个叶子结点返回depth即为最小深度

/**
 * 111 二叉树的最小深度
 */
public class Solution1 {

    /**
     * 层序遍历：分层遍历每一层元素，
     */
    public int minDepth(TreeNode root) {
        // root为null校验
        if (root == null) {
            return 0;
        }
        // 构建辅助队列
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);

        // 分层遍历
        int depth = 0; // 记录当前遍历层数
        while (!queue.isEmpty()) {
            // 分层遍历
            int curSize = queue.size();
            depth++; // 遍历当层层数
            for (int i = 0; i < curSize; i++) {
                // 取出元素
                TreeNode cur = queue.poll();

                // 如果当前节点为"当层的叶子结点"即没有左右节点，则直接返回（找到最小深度的节点了）
                if (cur.left == null && cur.right == null) {
                    return depth;
                }

                // 左右节点存在则入队
                if (cur.left != null) {
                    queue.offer(cur.left);
                }
                if (cur.right != null) {
                    queue.offer(cur.right);
                }
            }
        }
        return 0;
    }

}

（2）递归法
- 如果node为null说明为叶子节点，返回深度0
- 如果node不为null，且存在左子节点或者右子节点，则需讨论三种情况
  - left、right 都为 null：叶子节点
  - left、right 其中一个为 null：非叶子节点，需选择非null的子节点继续递归检索（left+right+1或者max{left,right}+1）因为left、right中肯定有一个为0所以这两个是等价的
  - left、right 两者都不为null，需选择较小的深度+1，即min{left,right}+1

/**
 * 111 二叉树的最小深度
 */
public class Solution2 {

    /**
     * 递归法
     */
    public int minDepth(TreeNode node) {
        /**
         * 递归出口的三种情况：
         * 1.node 为 null，返回 0
         * 2.node 不为 null
         * - 2.1 node.left 和 node.right 两者均为 null 说明到达叶子节点，因此返回 1
         * - 2.2 node.left 和 node.right 中其中一个为null，说明node不是叶子节点，需继续递归遍历
         *      - 此时递归那个不为null的子节点，也就是返回深度较大的节点+1，也可以理解为l+r+1（l、r其中一个肯定为0）
         * - 2.3 node.left 和 node.right 两个都不为null，则返回左右子节点最小的深度+1
         */
        //  node 为0的情况讨论
        if (node == null) {
            return 0;
        }
        // node 不为0的情况讨论（其left、right是否为null）
        // 1.left、right均为null，到了叶子结点
        if (node.left == null && node.right == null) {
            return 1;
        }
        /**
         * 2.left、right中其中一个为null，非叶子结点，需继续遍历非叶子节点的情况(即max{minDepth(left),minDepth(right)} + 1)
         * 即 可以理解为 要继续左右节点 中选择不为 null 的那个节点进行递归获取最小深度
         * 也可以简化为 max{minDepth(left),minDepth(right)} + 1  或者 minDepth(left)+minDepth(right) + 1 因为肯定是 0 + x + 1 的形式
         */
        if (node.left == null || node.right == null) {
            return Math.max(minDepth(node.left), minDepth(node.right)) + 1;
        }

        // 3.left、right都不为null，选择两者中最小深度+1
        return Math.min(minDepth(node.left), minDepth(node.right)) + 1;
    }

}

基于上述思路分析，简化版本（或者另一种描述形式）

/**
 * 111 二叉树的最小深度
 */
public class Solution3 {

    /**
     * 递归法
     */
    public int minDepth(TreeNode node) {
        //  node 为0的情况讨论
        if (node == null) {
            return 0;
        }
        // node 不为0的情况讨论（其left、right是否为null）
        int L = minDepth(node.left);
        int R = minDepth(node.right);

        // L == 0 || R == 0 左节点或者右节点为空
        if (L == 0 || R == 0) {
            return L == 0 ? R + 1 : L + 1;
//            return L + R + 1;
//            return Math.max(L, R) + 1;
        }
        // L != 0 && R != 0 左右节点都不为空
        return Math.min(L, R) + 1;
    }

}

🚀深度优先遍历（递归、迭代）

🤡深度优先遍历的统一迭代法open in new window

（1）递归法

🔔前序遍历（递归法）

/**
 * 144 二叉树的前序遍历
 */
public class Solution1 {
    public List<Integer> preorderTraversal(TreeNode root) {
        // 初始化递归结果集
        List<Integer> res = new ArrayList<>();
        preorder(root,res);
        return res;
    }

    // 递归方式实现前序遍历
    public void preorder(TreeNode node,List<Integer> list){
        // 递归出口
        if(node==null){
            return ;
        }
        // 递归过程（前序遍历DRL）
        list.add(node.val);
        preorder(node.left,list);
        preorder(node.right,list);
    }
}

🔔中序遍历（递归法）

/**
 * 094 二叉树的中序遍历
 */
public class Solution1 {
    public List<Integer> inorderTraversal(TreeNode root){
        // 定义遍历结果集
        List<Integer> res = new ArrayList<>();
        inorder(root,res);
        return res;
    }

    // 中序遍历（递归实现：LDR）
    public void inorder(TreeNode node,List<Integer> list){
        // 递归出口
        if(node==null){
            return ;
        }
        // 递归过程（LDR）
        inorder(node.left,list);
        list.add(node.val);
        inorder(node.right,list);
    }
}

🔔后序遍历（递归法）

/**
 * 145 二叉树的后序遍历
 */
public class Solution2 {
    List<Integer> postorderTraversal(TreeNode root){
        // 定义遍历结果集合
        List<Integer> res = new ArrayList<>();
        postorder(root,res);
        return res;
    }

    // 后序遍历（递归实现：LRD）
    public void postorder(TreeNode node,List<Integer> list){
        // 递归出口
        if(node==null){
            return;
        }
        // 递归过程（LRD）
        postorder(node.left,list);
        postorder(node.right,list);
        list.add(node.val);
    }
}

（2）迭代法

递归的实现核心：每一次递归调用都会把函数的局部变量、参数值和返回地址等压入调用栈中，然后递归返回的时候，从栈顶弹出上一次递归的各项参数

因此此处可以借助栈实现二叉树的前中后序遍历

前序遍历（DLR：迭代法）：与层次遍历的处理思路类似，此处是基于栈构建，处理节点后将左右节点分别入栈，左右节点的入栈顺序是先R后L（先入后出）
中序遍历（LDR：迭代法）：区分遍历和处理的顺序
后序遍历（LRD：迭代法）：逆向思考，将其转化为处理DLR的思路（LRD逆序为DRL，那么可以仿照DLR的思路构建DRL顺序，然后再逆序为LRD即可）

🔔前序遍历（迭代法）

前序遍历是：DLR，因此其思路是先将根节点入栈，然后取出节点（先遍历根节点）并分别将其右孩子、左孩子先后入栈（入栈顺序：先右后左），此处采取先右后左的思路是因为取出的时候要先取L再取R

结合代码实现可以看到这个思路和层序遍历很像（只不过此处用的是辅助栈存储，且遍历根节点的时候入栈顺序是先右后左）

// 迭代法：借助辅助栈实现
public List<Integer> preorderTraversal(TreeNode root) {
    // root 为null判断
    if(root==null){
        return new ArrayList<>();
    }

    // 初始化递归结果集
    List<Integer> res = new ArrayList<>();

    // 构建辅助栈
    Stack<TreeNode> stack = new Stack<>();
    stack.push(root); // 初始化将根节点入栈

    // 遍历栈元素
    while(!stack.isEmpty()){
        // 先遍历根节点
        TreeNode cur = stack.pop();
        res.add(cur.val);

        // 将当前根节点的右子节点、左子节点分别入栈（出栈时遍历才满足DLR顺序）
        if(cur.right!=null){
            stack.push(cur.right);
        }
        if(cur.left!=null){
            stack.push(cur.left);
        }
    }

    // 返回结果集
    return res;
}

在前序遍历的实现思路中，迭代的过程中涉及到两个操作：处理（将元素放入res结果集）、访问（遍历节点），前序遍历（DLR）中每次要处理的元素和遍历访问的元素顺序都是一致的，因此可以基于上述思路实现。但是对于中序遍历（LDR）而言，其思路是先访问二叉树顶部节点，然后一层层向下访问直到到达树左面的最底部再开始处理节点（将元素放入res结果集），实际这里的处理顺序和访问顺序是不一致的，因此无法仿照前序遍历迭代

因此中序遍历中，需要借助指针遍历来帮助访问节点，而栈则是用于处理节点元素

① 初始化：cur遍历指针（用于遍历节点）、stack栈（用于辅助处理节点）
② 遍历条件：当两者均不为空cur!=null && !stack.isEmpty()
- 如果cur!=null，则将遍历的节点依次入栈，并一直向左遍历（直到到达还未遍历的最左节点）
- 如果cur==null，说明达到了当前的最左节点，可以取出这个节点并将其值加入结果集，随后将cur指针指向其右节点

// 中序遍历（迭代法）LDR
public List<Integer> inorderTraversal(TreeNode root) {
    if (root == null) {
        return new ArrayList<>();
    }

    // 定义结果集
    List<Integer> res = new ArrayList<>();

    // 构建辅助栈
    Stack<TreeNode> stack = new Stack<>();
    TreeNode cur = root; // 定义cur指针用于遍历
    // 当指针不为空或者栈不为空时进行处理
    while (cur != null || !stack.isEmpty()) {
        if (cur != null) {
            stack.push(cur); // 将访问的节点入栈
            cur = cur.left; // 一直向左遍历直到到达最左的子节点
        } else {
            /*
                cur = stack.pop();
                res.add(cur.val);
                cur = cur.right;
                 */
            TreeNode node = stack.pop();
            res.add(node.val);
            cur = node.right;
        }
    }
    // 返回结果
    return res;
}

🔔后序遍历（迭代法）前序遍历（迭代法）的一种变体

后序遍历的思路实际上时前序遍历迭代法思路的一种变体：LRD反转后就是DRL，看到此处就会发现它和DLR的构造很像，也可以基于"处理顺序和遍历顺序相同"的思路去实现，因此对于LRD的实现可以反向思考：

思路分析： LRD 反转为 DRL 的顺序（可以仿照前序遍历的思路实现DRL：即先根节点入栈，然后左子节点、右子节点分别入栈）
算法实现：构建D->L->R的入栈顺序，得到D->R->L的出栈顺序，然后再将这个结果集反转得到LRD

// 迭代法
List<Integer> postorderTraversal(TreeNode root){
    if(root==null){
        return new ArrayList<>();
    }

    // 定义遍历结果集合
    List<Integer> res = new ArrayList<>();

    /**
         * 后序遍历（LRD）：反向操作
         * 思路分析： LRD 反转 为 DRL 的顺序（可以仿照前序遍历的思路实现DRL：即先根节点入栈，然后左子节点、右子节点分别入栈）
         * 算法实现：构建D->L->R的入栈顺序，得到D->R->L的出栈顺序，然后再将这个结果集反转得到LRD
         */

    // 构建辅助栈
    Stack<TreeNode> stack = new Stack<>();
    stack.push(root); // 初始化

    // 遍历栈
    while(!stack.isEmpty()){
        // 取出栈元素
        TreeNode cur = stack.pop();
        res.add(cur.val); // 先遍历D

        // 构建入栈顺序（先L后R）
        if(cur.left!=null){
            stack.push(cur.left);
        }
        if(cur.right!=null){
            stack.push(cur.right);
        }
    }

    // 最终反转结果集得到目标序列LRD
    Collections.reverse(res);

    // 返回结果集
    return res;
}

🟢翻转二叉树（226）

==核心思路：==反转二叉树的核心思路在于遍历每个节点，然后交换节点的左右子节点即可（因此可以中规中矩选择BFS、DFS方式进行遍历，然后对遍历到的节点进行左右子节点的交换即可）

1.题目内容open in new window

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点

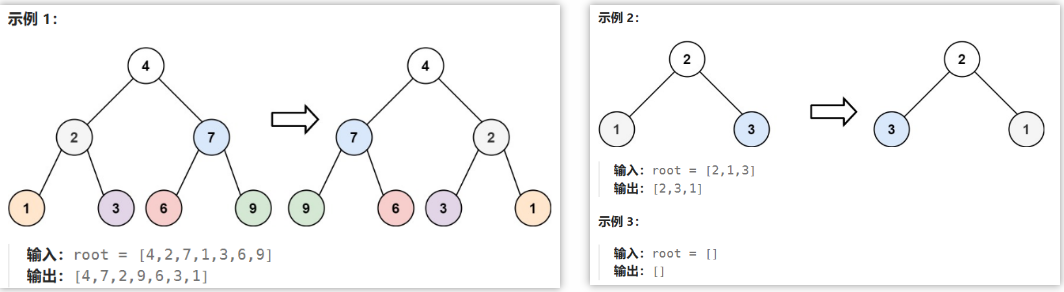
思路分析
- （1）层序遍历（BFS）：遍历每个节点，进行左右子节点两两交换
- （2）递归：左右子树交换

2.题解思路

👻方法1：层序遍历+交换

核心思路：基于层序遍历思路，遍历每个节点，然后进行左右子节点交换

/**
 * 226 翻转二叉树
 */
public class Solution1 {

    // 思路：层序遍历，依次遍历每个节点，交换其左右节点
    public TreeNode invertTree(TreeNode root) {
        // root 为 null
        if(root==null){
            return root;
        }

        // 构建辅助队列
        Deque<TreeNode> queue = new LinkedList<>();
        queue.offer(root); // 初始化队列

        // 遍历队列
        while(!queue.isEmpty()){
            // 取出元素，并交换其左右子节点
            TreeNode cur = queue.poll();
            // 交换(此处左右子节点的交换时机不受限入队前后，没有遍历需求，重在交换)
            TreeNode temp = cur.left;
            cur.left = cur.right;
            cur.right = temp;

            // 如果左右节点不为空则入队
            if(cur.left!=null){
                queue.offer(cur.left);
            }
            if(cur.right!=null){
                queue.offer(cur.right);
            }
        }

        // 返回结果
        return root;
    }
}

复杂度分析
- 时间复杂度：O（n）需遍历所有节点
- 空间复杂度：O（n）需借助队列辅助存储，最坏情况是root下有n-1个节点

👻方法2：DFS 递归+交换

核心思路：root 节点翻转转化为左右子树交换，层层递归，直到节点为null 的情况

/**
 * 226 翻转二叉树
 */
public class Solution2 {
    // 思路：递归法
    public TreeNode invertTree(TreeNode root) {
        invertNode(root);
        return root;
    }

    public void invertNode(TreeNode node){
        // 递归出口
        if (node == null) {
            return ;
        }
        // 递归过程
        // 交换左右节点
        TreeNode temp = node.left;
        node.left = node.right;
        node.right = temp;

        // 继续递归交换左右子节点
        invertNode(node.left);
        invertNode(node.right);
    }
}

复杂度分析
- 时间复杂度：O（n）需遍历所有节点
- 空间复杂度：O（n）取决于递归深度

🟢对称二叉树（101）

1.题目内容open in new window

给你一个二叉树的根节点 root ，检查它是否轴对称。

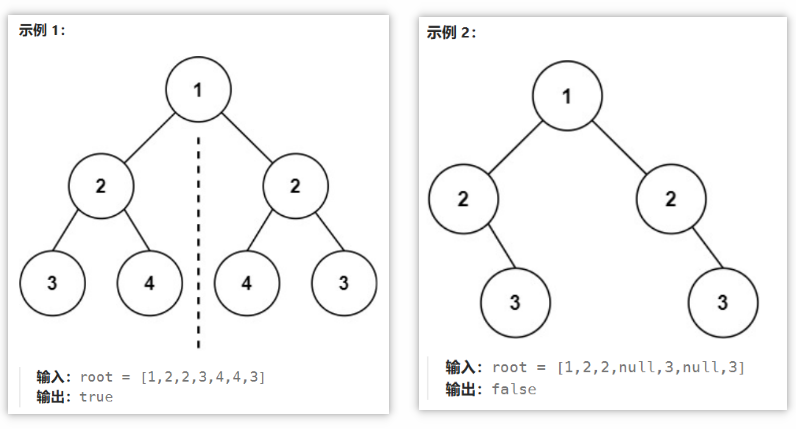
2.题解思路

👻方法1：递归法（节点对称 =》子树对称）

思路分析：判断两个节点是否对称，即判断两棵子树是否对称，两个对称节点的值是相等的

/**
 * 101 对称二叉树
 */
public class Solution1 {
    public boolean isSymmetric(TreeNode root) {
        // 调用递归方法，p、q 初始都从root开始
        // return check(root, root);
        return root == null || check(root.left, root.right); // 短路思路：root不为null才会执行左右子树对称判断
    }

    /**
     * 递归检查两个节点是否对称（此处传入两个要进行校验的对称节点）
     * 1.p、q 都为 null
     * 2.p、q 中某一个为 null
     * 3.p、q 都不为null，进一步校验两者的值是否相等，以及各自的左右子树是否也对称
     * - 此处左右子树是否对称是 p.left,q.right 对称节点比较、p.right,q.left 对称节点比较
     */
    public boolean check(TreeNode p, TreeNode q) {
        // 1.p、q 都为 null
        if (p == null && q == null) {
            return true; // 对称
        }

        // 2.p、q 中某一个为 null
        if (p == null || q == null) {
            return false; // 显然不对称
        }

        // 3.p、q 都不为null，进一步校验两者的值是否相等，以及各自的左右子树是否也对称
        return (p.val == q.val) && check(p.left, q.right) && check(p.right, q.left);
    }
}

复杂度分析
- 时间复杂度：O（n）
- 空间复杂度：空间复杂度与递归使用的占空间有关

递归法的另一种写法：也可以理解为遍历两棵树，判断对应位置的节点是否匹配
p.left 与 q.right 为一组进行校验；p.right 与 q.left 为一组进行校验

/**
 * 🟢 101 对称二叉树
 */
public class Solution101_01 {

    /**
     * 递归法：结合对称二叉树特性处理
     * 基于dfs思路：可以用两个指针节点进行遍历，看每个指针指向的位置是否匹配
     */
    public boolean isSymmetric(TreeNode root) {
        // 调用递归方法处理
        return dfs(root, root);
    }

    /**
     * 对同一棵树用两个指针分别进行遍历，校验节点对应位置是否匹配。根据 p、q进行null判断
     */
    public boolean dfs(TreeNode p, TreeNode q) {
        // ① 两个节点如果都为null则匹配
        if (p == null && q == null) {
            return true;
        }
        // ② 如果只有一个节点为null则不匹配
        if ((p == null && q != null) || (p != null && q == null)) {
            return false;
        }
        // ③ 如果两个都不为null，则校验值是否匹配
        if (p != null && q != null) {
            if (p.val != q.val) { // 如果校验的两个节点均不为空，则校验值是否匹配，如果不匹配则返回false
                return false;
            }
        }

        // 递归处理节点：校验对称性（各自的左子树与右子树交叉匹配）
        boolean validLeft = dfs(p.left, q.right);
        boolean validRight = dfs(p.right, q.left);
        return validLeft && validRight;
    }
}

👻方法2：迭代法（两两比较对称节点）

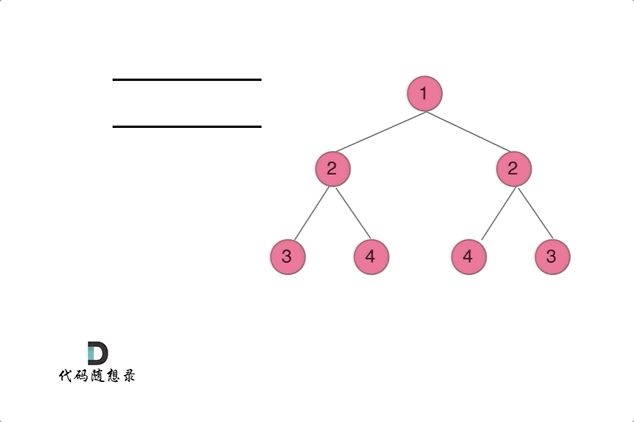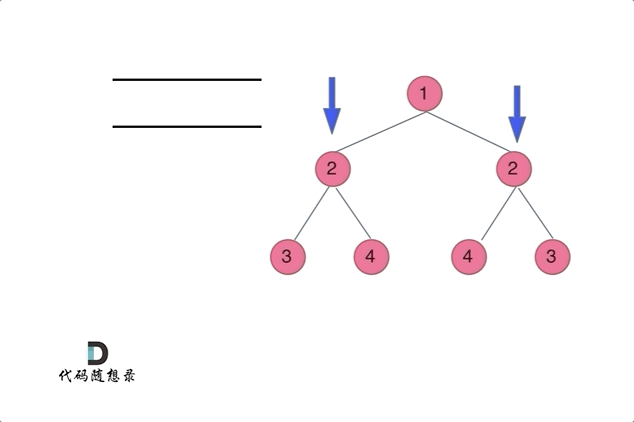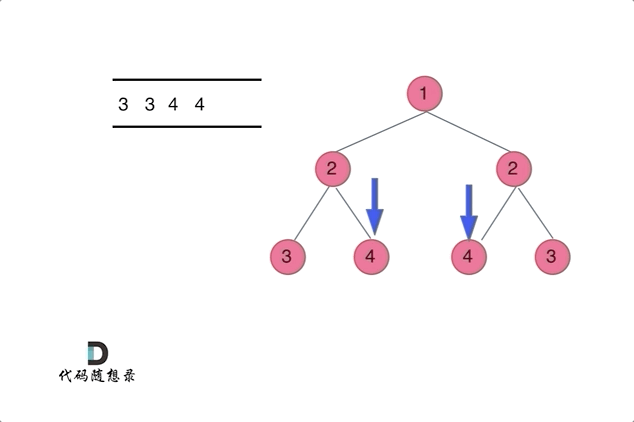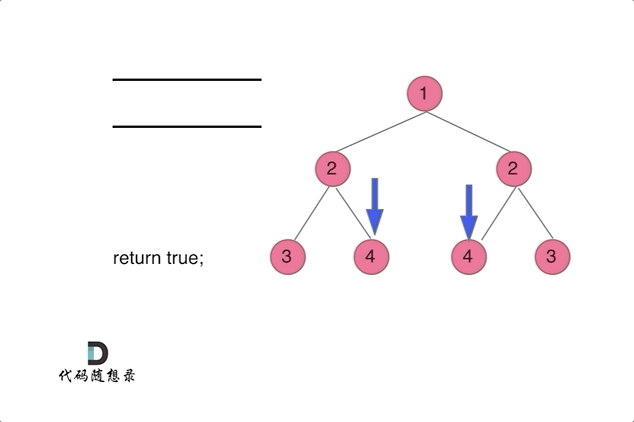
思路分析：相当于同时遍历树，一个遍历左一个遍历右，可以用一个队列或者两个队列辅助
- 基于层序遍历的思路，定义一个队列初始化加入root两次，然后后续迭代过程中每次取出两个节点进行比较
- 每次遍历取出两个待比较的对称节点：判断val是否一致
- 入队：按照要进行比较的对称节点分组进行先后入队（才能确保每次取出的是待比较的对称节点），例如进入root1、root2
  - root1.left与root2.right是一组【待比较的对称节点】、root1.right与root2.left是一组【待比较的对称节点】，按照组别先后入队
  - null节点是否需要入队？=》null节点也要入队，用null节点占位，避免下面这种情况覆盖不到，且如果将null节点入队，相应需要做NPE判断处理（即取出的两个节点为null则这种情况是匹配对称的，跳过本轮校验继续下一组即可）

/**
 * 101 对称二叉树
 */
public class Solution2 {
    /**
     * 层序遍历思路：初始化将root载入两次
     * 后续遍历每次取出两个节点进行比较，如果验证通过相应将左右节点按照分组（待比较的对称节点为一组）进行先后入队
     */
    public boolean isSymmetric(TreeNode root) {
        // root 为null判断
        if (root == null) {
            return true;
        }

        // 构建辅助队列
        Deque<TreeNode> queue = new LinkedList<>();
        // 初始化载入两个root节点（用作同时遍历左右子树进行校验）
        queue.offer(root);
        queue.offer(root);

        // 遍历队列
        while (!queue.isEmpty()) {
            // 每次取出两个节点进行比较：root1、root2
            TreeNode node1 = queue.poll();
            TreeNode node2 = queue.poll();

            // 比较两个节点的值是否相同，如果不相同说明不对称，直接返回false
            // 如果两个节点都为null，跳出当轮比较
            if (node1 == null && node2 == null) {
                continue; // 两个节点都为null 无需比较（满足条件，跳过本轮后续的内容）
            }
            // 如果两个节点某一方不存在
            if (node1 == null || node2 == null) {
                return false;
            }
            // 如果两个节点的值存在
            if (node1.val != node2.val) {
                return false;
            }

            /**
             * 如果两个节点的值相同，则继续载入左右节点进行下一轮比较（此处需注意节点的入队顺序，确保每一轮进去的节点按照【待校验的对称节点】进行分组）
             * 即 node1.left 和 node2.right 是一组【待验证的对称节点】、node1.right 和 node2.left 是一组【待验证的对称节点】
             * 只有按照这个顺序入队，才能确保每次两两比较时验证对称的有效性
             */
            // node1.left 和 node2.right 是一组【待验证的对称节点】
            queue.offer(node1.left); // 此处不做子节点的null校验，是为了避免null节点带来的影响，用null占空位
            queue.offer(node2.right);
            // node1.right 和 node2.left 是一组【待验证的对称节点】
            queue.offer(node1.right);
            queue.offer(node2.left);
        }
        // 所有验证通过，说明树是对称的
        return true;
    }

}

复杂度分析
- 时间复杂度：O（n）需遍历所有节点
- 空间复杂度：O（n）需借助队列辅助校验，相当于用一个队列同时遍历两棵树的不同位置

迭代法的另一种写法：双队列 BFS 遍历

/**
 * 🟢 101 对称二叉树
 */
public class Solution101_03 {

    /**
     * 迭代法：构建双队列对树进行比较
     */
    public boolean isSymmetric(TreeNode root) {
        return bfs(root, root);
    }

    // 层序遍历
    public boolean bfs(TreeNode p, TreeNode q) {
        // 构建辅助队列处理
        Queue<TreeNode> pQueue = new LinkedList<>();
        Queue<TreeNode> qQueue = new LinkedList<>();
        pQueue.offer(p);
        qQueue.offer(q);
        // 校验两个队列
        while (!pQueue.isEmpty() && !qQueue.isEmpty()) {
            // 每次取出两个队列的节点进行处理
            TreeNode curP = pQueue.poll();
            TreeNode curQ = qQueue.poll();

            // 对curP、curQ 分情况讨论
            // ① curP和curQ均为空，说明匹配（校验符合，跳过本次处理）
            if (curP == null && curQ == null) {
                continue;
            }
            // ② curP、curQ中只有一个为空，说明不匹配
            if ((curP == null && curQ != null) || (curP != null && curQ == null)) {
                return false;
            }
            // ③ curP、curQ中均不为空，校验值是否匹配
            if (curP != null && curQ != null) {
                if (curP.val != curQ.val) {
                    return false;
                }
            }

            /**
             * 处理左右节点
             * 对称性校验是两棵树的左右子节点交叉校验：所以要确保每次入队的两个节点是待比较组
             * 此处使用同一个队列，则正常将待比较组入栈即可，每次取出两个节点进行比较
             * 如果使用不同队列处理，要确保结构一致，则对于空节点也要正常入队
             */
            pQueue.offer(curP.left);
            qQueue.offer(curQ.right);
            pQueue.offer(curP.right);
            qQueue.offer(curQ.left);
        }
        // 校验节点
        // return true; // 此处是同一棵树的比较，所以两个队列肯定完全一致，只要通过上述校验即可。但是如果是不同树的对称比较此处还需考虑两个队列是否有剩余节点的情况（例如【相同的树】）
        return pQueue.isEmpty() && qQueue.isEmpty();
    }
}

3.扩展内容

本题的解题思路和另外两道的解题思路是类似的，可以适当举一反三学习

100. 相同的树open in new window

此处唯一不同的点在于入队顺序，对称节点是左右、右左比较、相同树是左左、右右比较

/**
 * 🟢100 相同的树
 */
public class Solution100_02 {

    /**
     * 迭代法：
     * 如果两个树结构完全相同，则其遍历顺序应完全一致（此处需注意对于空节点需占位，才能确保结构一致）
     * 单队列思路：用一个队列接收两棵树的节点，每次取出两个节点校验，如果完全一致则认为两棵树的结构相同
     * - 此处需注意对非叶子结点的左右子节点的非空占位讨论，此处采取的方案是对于非叶子节点的左右节点均入队，然后再取出节点校验是否匹配的时候进行分情况讨论
     * - 由于不限定入队的子节点是否为空，因此需要对取出的两个节点进行null讨论
     * - ① curP、curQ 均为空，则说明匹配，跳过后面的子节点处理
     * - ② curP、curQ 中只有一个为null，说明不匹配（预期取出的两个节点要完全一致的，所以此处不需要讨论为什么只有一个为null。只要不匹配就返回false）
     * - ③ curP、curQ 两者均不为null，校验值是否匹配（若不匹配直接返回false），随后需要处理各自的左右子节点入队（p左q左、p右q右）
     */
    public boolean isSameTree(TreeNode p, TreeNode q) {
        // 构建队列辅助遍历元素
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(p);
        queue.offer(q);

        while (!queue.isEmpty()) {
            // 每次校验取出队列的两个元素进行比较
            TreeNode curP = queue.poll();
            TreeNode curQ = queue.poll();

            // 此处限定空节点也可以入队占位，所以要对null的情况进行处理
            // ① 如果取到的两个节点都为空，则说明匹配，且两个节点都为空可以直接跳过后面的子节点处理
            if (curP == null && curQ == null) {
                continue;
            }

            // ② 如果取到的两个节点有一个为空则不匹配，返回false
            if ((curP == null && curQ != null) || (curP != null && curQ == null)) {
                return false;
            }

            // ③ 如果两个均为非空节点，且值不匹配则返回false
            if (curP.val != curQ.val) {
                return false; // 节点对应不一致，结构不同
            }

            // 处理两棵树的左右子树节点（p左q左、p右q右）：按照待比较元素分组,就算是null节点也要占位，确保顺序一致
            queue.offer(curP.left);
            queue.offer(curQ.left);
            queue.offer(curP.right);
            queue.offer(curQ.right);
        }

        // 校验通过说明一致
        return true;
    }
}

双队列遍历比较（分别定义两个队列存储两棵树的遍历顺序（此处注意对于非叶子节点的左右节点为空的情况需要用临时节点占位，才能确保结构完全一致））

/**
 * 🟢100 相同的树
 */
public class Solution100_01 {

    public int tempVal = -999999; // 设计一个非限定范围的值，用于占位（标记null节点）

    /**
     * 迭代法：
     * 如果两个树结构完全相同，则其遍历顺序应完全一致（此处需注意对于空节点需占位，才能确保结构一致）
     */
    public boolean isSameTree(TreeNode p, TreeNode q) {
        if (p == null && q == null) {
            return true;
        }
        if ((p == null && q != null) || (p != null && q == null)) {
            return false;
        }

        // 构建队列辅助遍历元素
        Queue<TreeNode> pQueue = new LinkedList<>();
        pQueue.offer(p);

        Queue<TreeNode> qQueue = new LinkedList<>();
        qQueue.offer(q);

        while (!pQueue.isEmpty() && !qQueue.isEmpty()) {
            // 分别取出两个队列的元素，然后进行一一匹配比较
            TreeNode curP = pQueue.poll();
            TreeNode curQ = qQueue.poll();
            if (curP.val != curQ.val) {
                return false; // 节点对应不一致，结构不同
            }
            // 处理两棵树的左右子树
            if (!(curP.left == null && curP.right == null)) { // 对于非叶子结点
                pQueue.offer(curP.left == null ? new TreeNode(tempVal) : curP.left); // 对于null节点也要进行占位
                pQueue.offer(curP.right == null ? new TreeNode(tempVal) : curP.right); // 对于null节点也要进行占位
            }
            if (!(curQ.left == null && curQ.right == null)) { // 对于非叶子结点
                qQueue.offer(curQ.left == null ? new TreeNode(tempVal) : curQ.left); // 对于null节点也要进行占位
                qQueue.offer(curQ.right == null ? new TreeNode(tempVal) : curQ.right); // 对于null节点也要进行占位
            }
        }

        // 如果两个队列都遍历完成（最终为空），则说明完全一致
        return pQueue.isEmpty() && qQueue.isEmpty();

    }
}

递归思路：判断两棵树是否结构完全一致，则需满足根节点匹配，则其左右子树也一一匹配，基于此可以采用递归的思路处理

/**
 * 🟢100 相同的树
 */
public class Solution100_03 {

    /**
     * 递归法：判断两棵树是否结构完全一致，则需满足根节点匹配，则其左右子树也一一匹配，基于此可以采用递归的思路处理
     * - 递归处理的核心在于讨论节点在什么情况下要匹配，且需要讨论节点为空的情况（实际和迭代法讨论的情况类似）
     */
    public boolean isSameTree(TreeNode p, TreeNode q) {

        /**
         * 递归出口：讨论p、q节点的null情况
         * ① p、q 均不为 null：两个节点匹配，返回true
         * ② p、q 中仅有一个为 null：两个节点无法匹配，返回false
         * ③ p、q 均为 null：需进一步校验两个节点的val是否匹配，根据校验结果处理，如果不匹配则返回false
         * 对于节点而言，其左右子树也要相应匹配
         */
        if (p == null && q == null) {
            return true;
        }

        if ((p == null && q != null) || (p != null && q == null)) {
            return false;
        }

        if (p != null && q != null) {
            if (p.val != q.val) {
                return false;
            }
        }

        // 递归处理
        boolean validLeft = isSameTree(p.left, q.left);
        boolean validRight = isSameTree(p.right, q.right);
        return validLeft && validRight;
    }
}

572.另一棵树的子树open in new window
- 思路：硬核遍历节点判断当前节点所在位置的子树是否和目标子树相同，将解决方案转化为遍历节点+相同的树判断
  - 此处注意剪枝判断：只有两个节点的根节点都一致才有必要继续往下判断【相同的树】

/**
 * 572 另一颗树的子树
 */
public class Solution1 {

    public boolean isSubtree(TreeNode root, TreeNode subRoot) {
        /**
         * 遍历root的每个节点，判断当前遍历节点cur所在位置是否和subRoot子树完全相同
         * - 此处不需要每个节点都去过一遍子树，先判断当前遍历节点cur的值和subRoot的值是否一致，一致才有继续比较的必要性，不一致则跳过
         */
        // root、subRoot均为null
        if (root == null && subRoot == null) {
            return true;
        }

        // root、subRoot 一方为null
        if (root == null || subRoot == null) {
            return false;
        }

        // root、subRoot均不为null
        Deque<TreeNode> queue = new LinkedList<>();
        queue.offer(root);

        while (!queue.isEmpty()) {
            TreeNode cur = queue.poll();
            if (cur.val == subRoot.val) {
                // 进一步比较
                if (isSameTree(cur, subRoot)) {
                    return true; // 存在相同子树则返回true
                }
            }

            // 将左右子节点入队
            if (cur.left != null) {
                queue.offer(cur.left);
            }
            if (cur.right != null) {
                queue.offer(cur.right);
            }
        }
        // 如果上述比较结果中没有满足的内容，说明不存在子树
        return false;
    }

    // 迭代法：定义队列辅助存储（此处可以使用两个队列，也可使用同一个队列按层遍历即可），每次同步存入两个元素，同步取出两个元素进行比较
    public boolean isSameTree(TreeNode p, TreeNode q) {
        // 构建辅助队列
        Deque<TreeNode> queue = new LinkedList<>(); // 此处使用1个队列，确保数据插入顺序是按照待比较元素分组
        queue.offer(p);
        queue.offer(q);

        // 遍历队列
        while (!queue.isEmpty()) {
            // 每次取出两个元素进行比较
            TreeNode node1 = queue.poll();
            TreeNode node2 = queue.poll();

            // 如果node1、node2均为null
            if (node1 == null && node2 == null) {
                continue; // 满足条件，直接进入下一轮比较
            }
            // 如果node1、node2一方为null
            if (node1 == null || node2 == null) {
                return false; // 不匹配，直接返回false
            }
            // 如果node1、node2均不为null
            if (node1.val != node2.val) {
                return false; // 两个节点的值不匹配，直接返回false
            }

            // 将节点存入队列（按照待比较元素分组,就算是null节点也要占位，确保顺序一致）
            queue.offer(node1.left);
            queue.offer(node2.left);
            queue.offer(node1.right);
            queue.offer(node2.right);
        }
        // 经过上述校验，验证相同的树
        return true;
    }
}

🍚02-二叉树的深度问题（基于上述BFS扩展题型）

🟢二叉树的最大深度
🟢N叉树的最大深度
🟢二叉树的最小深度

🟢104-二叉树的最大深度

1.题目内容open in new window

给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数

2.题解思路

核心思路：最大深度，可以理解为求树的高度（根节点的高度），可以基于两种遍历方式思考

① 对于BFS：计算的是分层遍历的层数
② 对于DFS：基于当前遍历节点的高度计算思考，当前节点的高度为max{leftTree,rightTree}+1(即当前节点的左右子树的最大高度+1)，在递归的过程中计算处理即可

👻方法1：递归法

/**
 * 🟢 104 二叉树的最大深度
 */
public class Solution104_01 {

    /**
     * 递归法：
     * 当前树的高度（最大深度） = max{leftTree,rightTree} + 1
     * 即当前节点的高度为其左、右子节点的最大高度 + 1
     */
    public int maxDepth(TreeNode root) {
        int maxDepth = dfs(root);
        return maxDepth;
    }

    public int dfs(TreeNode node) {
        // 递归出口
        if (node == null) { // 叶子节点高度为0
            return 0;
        }
        // 递归计算左、右子节点的高度
        int leftTree = dfs(node.left);
        int rightTree = dfs(node.right);
        // 返回最大高度
        return Math.max(leftTree, rightTree) + 1;
    }
}

👻方法2：迭代法

/**
 * 🟢 104 二叉树的最大深度
 */
public class Solution104_02 {

    // 迭代法
    public int maxDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int maxDepth = bfs(root);
        return maxDepth;
    }

    // 层序遍历思路：最大深度即计算树的高度，基于层序遍历即计算分层数
    public int bfs(TreeNode node) {
        // 构建队列辅助遍历
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(node);
        // 定义层数
        int maxDepth = 0;
        // 遍历队列
        while (!queue.isEmpty()) {
            // 获取当层节点个数，处理当层数据
            int cnt = queue.size();
            while (cnt-- > 0) {
                // 取出节点处理
                TreeNode cur = queue.poll();
                // 处理左右节点
                if (cur.left != null) {
                    queue.offer(cur.left);
                }
                if (cur.right != null) {
                    queue.offer(cur.right);
                }
            }
            // 当层处理结束，累计层数
            maxDepth++;
        }
        // 返回结果
        return maxDepth;
    }

}

🟢559-N叉树的最大深度

1.题目内容open in new window

2.题解思路

👻方法1：回溯法

求出所有路径，然后找到路径的最大值

/**
 * 🟢559 N叉树的最大深度
 */
public class Solution559_01 {

    // List<List<Integer>> res = new ArrayList<>();
    int maxLevel = 0; // 此处只需统计路径的最大值
    List<Integer> path = new ArrayList<>();

    public int maxDepth(Node root) {
        if (root == null) {
            return 0;
        }

        // 初始化将root节点值加入路径
        path.add(root.val);
        // 调用回溯算法
        backTrack(root);
        // 返回结果
        return maxLevel;
    }

    // 回溯法：获取所有路径，取最大深度（最长路径）
    public void backTrack(Node node) {
        // 递归出口
        if (node == null) {
            return;
        }

        // 当遍历到叶子节点，找到一条路径(叶子节点即表示children为空)
        if (node.children.isEmpty()) {
            // res.add(new ArrayList<>(path));
            maxLevel = Math.max(maxLevel, path.size());
        }

        // 递归回溯处理获取所有路径
        for (Node child : node.children) {
            if (child != null) {
                path.add(child.val); // 处理节点
                backTrack(child); // 递归
                path.remove(path.size() - 1); // 恢复现场
            }
        }
    }
}

// 定义N叉树节点 NTreeNode
class Node {
    int val;
    List<Node> children;
}

👻方法2：BFS

和二叉树相关题型的BFS处理类似，基于层序遍历，只不过此处每次处理不是两个节点(左右节点)，而是节点列表，相应调整为节点列表处理即可

/**
 * 🟢559 N叉树的最大深度
 */
public class Solution559_02 {

    public int maxDepth(Node root) {
        return bfs(root);
    }

    // BFS： 基于 N 叉树的层序遍历，计算层数
    public int bfs(Node node) {
        if (node == null) {
            return 0;
        }

        // 构建队列辅助遍历
        Queue<Node> queue = new LinkedList<>();
        queue.offer(node); // 初始化

        int level = 0; // 计算层数

        while (!queue.isEmpty()) {
            int cnt = queue.size();
            while (cnt-- > 0) {
                // 取出当前节点
                Node cur = queue.poll();

                // 将节点的子节点列表入队
                for (Node child : cur.children) {
                    if (child != null) {
                        queue.offer(child);
                    }
                }
            }
            level++; // 当层处理完成，统计level
        }

        // 返回层数
        return level;
    }
}

👻方法3：DFS

和二叉树相关题型的DFS处理类似，基于递归处理，求某个节点的最大深度，即为max{child1,child2....childN} + 1(即递归获取其子节点的的最大深度选择最大的那个 + 1 即可)

/**
 * 🟢559 N叉树的最大深度
 */
public class Solution559_03 {

    // DFS 方式
    public int maxDepth(Node root) {
        return dfs(root);
    }

    // 计算节点深度
    public int dfs(Node node) {
        // 递归出口
        if (node == null) {
            return 0;
        }
        // 递归计算每个子节点的深度，选择最大的深度
        int max = 0;
        for (Node child : node.children) {
            max = Math.max(max, dfs(child));
        }
        // 返回节点最大深度
        return max + 1;
    }
}

🟢111-二叉树的最小深度

1.题目内容open in new window

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

**说明：**叶子节点是指没有子节点的节点。

2.题解思路

① 模拟法：
- 【模拟思路】得到根节点到每个叶子节点的路径path，然后得到这些路径的最小节点个数
② BFS：层序遍历，从上到下从左到右，遇到的第一个叶子节点，这个叶子结点的高度（所在层次）即为二叉树的最小深度
③ DFS：基于节点高度理解，计算每个节点的高度，每次选择最小高度（根据节点是否为null，是否为叶子节点进行情况划分）
- 如果node为null，返回0
- 如果node不为null（校验左右子节点的情况）
  - 叶子结点：返回1
  - 非叶子节点：
    - 两个当中只有一个为null，需选择继续递归不为null的那个节点深度
    - 两个都不为null，返回较小的深度

👻方法1：回溯法（回溯：路径处理）

思路分析：转化为路径处理问题，处理根节点到每个叶子节点的路径，计算路径节点个数，返回最小值
- ==误区：==一开始采用StringBuffer来追加路径，但此处不同于【129 求根节点到叶节点数字之和】，不可以单纯采用字符串拼接（存在负数的情况，且数值大小不限制，直接用拼接的方式计算path长度的话就会出现问题）。如果要采用StringBuffer追加路径的话，则需要考虑加入分隔符来区分不同的节点，否则单纯根据字符串长度来判断路径长度的话就会出现问题，例如节点出现负数或者值超出1位的话就会出现-8-12612这种情况，无法界定节点（需加入分割符处理）。或者直接用List<Integer>记录path路径节点（不易出错）可通过断点分析路径是否遍历正确

/**
 * 🟢 111 二叉树的最小深度
 */
public class Solution111_01 {

    public List<List<Integer>> res = new ArrayList<>();
    // 此处不同于【129 求根节点到叶节点数字之和】，不可以采用字符串拼接（存在负数的情况，且数值大小不限制，直接用拼接的方式计算path长度的话就会出现问题）
    // public StringBuffer path = new StringBuffer();
    List<Integer> path = new ArrayList<>();


    // 规律分析：计算每个叶子节点的路径的节点个数，取最小值
    public int minDepth(TreeNode node) {
        if (node == null) {
            return 0;
        }
        // 初始化将root节点加入路径
        path.add(node.val);

        // ① 调用dfs方法获取所有路径,得到最小的路径
        dfs(node);

        // ② 计算最小路径
        int minDepth = Integer.MAX_VALUE;
        for (List<Integer> path : res) {
            minDepth = Math.min(path.size(), minDepth);
        }
        return minDepth;
    }


    // 递归辅助计算根节点到每个叶子节点的路径的节点个数
    public void dfs(TreeNode node) {
        if (node == null) {
            return;
        }

        // 遇到叶子节点，添加路径
        if (node.left == null && node.right == null) {
            res.add(new ArrayList<>(path)); // 此处注意对象引用问题，添加一个新的String对象，避免回溯过程中的对象引用变化
        }

        // 处理节点
        if (node.left != null) {
            path.add(node.left.val);
            dfs(node.left);
            path.remove(path.size() - 1);
        }
        if (node.right != null) {
            path.add(node.right.val);
            dfs(node.right);
            path.remove(path.size() - 1);
        }
    }

    public static void main(String[] args) {
        TreeNode node1 = new TreeNode(-8);
        TreeNode node2 = new TreeNode(-6);
        TreeNode node3 = new TreeNode(7);
        TreeNode node4 = new TreeNode(6);
        TreeNode node5 = new TreeNode(5);
        node1.left = node2;
        node1.right = node3;
        node2.left = node4;
        node4.right = node5;
        Solution111_01 s = new Solution111_01();
        s.minDepth(node1);
    }
}

版本简化：

此处只需要计算路径节点个数的最小值，那么只需要在得到一条路径同步判断得到minDepth即可，不用存储所有路径的完整信息

/**
 * 🟢 111 二叉树的最小深度
 */
public class Solution111_011 {

    int minDepth = Integer.MAX_VALUE; // 记录[根节点->叶子节点]的每条路径的最小节点个数
    List<Integer> path = new ArrayList<>();

    // 规律分析：计算每个叶子节点的路径的节点个数，取最小值
    public int minDepth(TreeNode node) {
        if (node == null) {
            return 0;
        }
        // 初始化将root节点加入路径
        path.add(node.val);

        // ① 调用dfs方法获取所有路径,得到最小的路径
        dfs(node);

        // ② 计算最小路径（在遍历路径的时候同步处理）
        return minDepth;
    }


    // 递归辅助计算根节点到每个叶子节点的路径的节点个数
    public void dfs(TreeNode node) {
        if (node == null) {
            return;
        }

        // 遇到叶子节点，添加路径
        if (node.left == null && node.right == null) {
            // 更新minDepth
            minDepth = Math.min(minDepth, path.size());
        }

        // 处理节点
        if (node.left != null) {
            path.add(node.left.val);
            dfs(node.left);
            path.remove(path.size() - 1);
        }
        if (node.right != null) {
            path.add(node.right.val);
            dfs(node.right);
            path.remove(path.size() - 1);
        }
    }
}

另一种写法（对节点的null校验位置不同）

/**
 * 🟢 111 二叉树的最小深度 - https://leetcode.cn/problems/minimum-depth-of-binary-tree/description/
 */
public class Solution111_03 {
    
    // 最小深度
    int minDepth = Integer.MAX_VALUE;
    // 定义路径
    List<TreeNode> path = new ArrayList<>();

    /**
     * 思路分析：最小深度（根节点到最近的叶子节点的最短路径上的节点数量）
     * 基于递归回溯的思路（最小深度，即求最短路径的节点个数，可基于回溯的思路处理）
     */
    public int minDepth(TreeNode root) {
        // 根节点载入路径
        path.add(root);
        // 调用回溯算法
        backTrack(root);
        // 返回最小深度
        return minDepth == Integer.MAX_VALUE ? 0 : minDepth;
    }

    // 回溯法
    private void backTrack(TreeNode node) {
        // 递归出口
        if (node == null) {
            return;
        }

        // 遍历到叶子节点
        if (node.left == null && node.right == null) {
            // 记录当前路径的最小值
            minDepth = Math.min(minDepth, path.size()); // 节点个数为当前路径的遍历节点
        }

        // 遍历选择（回溯处理：选择左、右子节点）
        path.add(node.left); // 选择左节点
        backTrack(node.left); // 递归处理
        path.remove(path.size() - 1); // 恢复现场

        path.add(node.right); // 选择右节点
        backTrack(node.right); // 递归处理
        path.remove(path.size() - 1); // 恢复现场
    }

}

👻方法2：`BFS`思路

思路分析：基于层次遍历（从上到下、从左到右），找到第一个叶子结点，这个叶子结点所在位置就是最短路径

/**
 * 🟢 111 二叉树的最小深度
 */
public class Solution111_02 {

    // BFS 层次遍历：从上到下、从左到右，搜索到第一个叶子结点直接返回层数（即为最短路径）
    public int minDepth(TreeNode node) {
        if (node == null) {
            return 0;
        }

        // 记录遍历层数
        int level = 0;

        // 构建队列辅助遍历
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(node);

        while (!queue.isEmpty()) {
            // 计算当层节点个数
            int cnt = queue.size();
            while (cnt-- > 0) {
                TreeNode cur = queue.poll();
                // 处理节点（如果为叶子节点，则直接返回）
                if (cur.left == null && cur.right == null) {
                    return level + 1; // 返回的是每个路径的节点个数，因此此处返回的是层数+1
                }

                // 节点入队
                if (cur.left != null) {
                    queue.offer(cur.left);
                }
                if (cur.right != null) {
                    queue.offer(cur.right);
                }
            }
            // 当层遍历结束
            level++;
        }
        return 0;
    }
}

👻方法3：`DFS`思路

思路分析：
- node==null：递归出口
- node!=null：进一步根据节点的左右节点是否为空分情况讨论（区分叶子节点、非叶子节点）
  - ① 左右节点均为空（叶子节点）：
  - ② 左右节点中只有一个为空（非叶子结点）：选择不为空的那个节点继续遍历获取深度（因为最小深度获取的是根节点到叶子节点的min概念）
  - ③ 左右节点均为空（非叶子结点）：选择较小的深度返回

/**
 * 🟢 111 二叉树的最小深度
 */
public class Solution111_03 {

    // DFS
    public int minDepth(TreeNode node) {
        return dfs(node);
    }

    public int dfs(TreeNode node) {
        // 递归出口
        if (node == null) {
            return 0;
        }

        // 根据node的左右节点是否为null分情况讨论
        TreeNode L = node.left, R = node.right;

        // ① 如果左右节点都为null，到了叶子节点返回1(此处返回的是最短路径的节点个数，因此返回的是1)
        if (L == null && R == null) {
            return 1;
        }
        // ② 如果左、右节点有一个为null，则需要选择不为null的节点继续递归遍历深度
        if ((L == null && R != null) || (L != null && R == null)) {
            // return Math.max(minDepth(L), minDepth(R)) + 1;
            return dfs(L) + dfs(R) + 1; // 也可以是 minDepth(L) + minDepth(R) + 1，即l+r+1（因为这种情况下l、r中肯定有一个为0）
        }

        // ③ 如果左右节点均不为null，则递归选择两者中较小的深度返回
        return Math.min(dfs(node.left), dfs(node.right)) + 1;
    }

}

🍚03-二叉树特性考察（不同二叉树特性应用技巧解题）

🟢完全二叉树的节点个数（222）

1.题目内容open in new window

给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。

完全二叉树open in new window 的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。

2.题解思路

【1】硬核遍历：BFS、DFS 遍历所有节点，然后统计节点个数
【2】递归法：利用完全二叉树的特性，对递归过程进行优化
- 递归核心：以当前节点为根节点（把每个节点当作一个根节点）的子树的节点个数，其可以由L+R+1来递归得出，即以其左子节点为根节点的子树的节点个数 + 以其右子节点为根节点的子树的节点个数 + 自身节点（1）得到
- 分类说明：区分满二叉树和普通二叉树的节点统计来处理
  - 满二叉树的校验：左、右子树的深度相同（分别定义左/右指针一直向左/向右遍历直到叶子节点获取子树深度）
  - 满二叉树的节点个数为2^h-1，而普通二叉树的节点个数则可通过递归方式获取
  - 关注递归核心L+R+1，则L、R的节点个数统计则可根据L、R子树属性进行分类统计即可

👻方法1：遍历法（DFS）

思路分析：通过BFS、DFS遍历节点，然后进行计数统计
- DFS（LRD）

public class Solution1 {

    public int countNodes(TreeNode root) {
        if (root == null) {
            return 0;
        }
        return dfs(root);
    }

    public int dfs(TreeNode node) {
        if (node == null) {
            return 0;
        }
        int leftCnt = dfs(node.left); // L
        int rightCnt = dfs(node.right); // R
        return leftCnt + rightCnt + 1; // D（左节点个数+右节点个数+1）
    }

}

复杂度分析
- 时间复杂度：O（n）遍历所有节点
- 空间复杂度：空间复杂度取决于递归占用

其他写法思路

/**
 * 🟢 222 完全二叉树的节点个数 - https://leetcode.cn/problems/count-complete-tree-nodes/description/
 */
public class Solution222_02 {

    private int cnt;

    public int countNodes(TreeNode root) {
        // 调用递归算法
        dfs(root);
        // 返回结果
        return cnt;
    }

    private void dfs(TreeNode node) {
        // 递归出口
        if (node == null) {
            return;
        }
        // DLR
        cnt++; // 统计节点
        dfs(node.left); // 递归处理左节点
        dfs(node.right); // 递归处理右节点
    }
}

/**
 * 🟢 222 完全二叉树的节点个数 - https://leetcode.cn/problems/count-complete-tree-nodes/description/
 */
public class Solution222_03 {

    public int countNodes(TreeNode root) {
        // 调用递归算法
        List<Integer> list = new ArrayList<>();
        dfs(root, list);
        // 返回结果
        return list.size();
    }

    private void dfs(TreeNode node, List<Integer> list) {
        // 递归出口
        if (node == null) {
            return;
        }
        // DLR
        list.add(node.val); // 统计节点
        dfs(node.left, list); // 递归处理左节点
        dfs(node.right, list); // 递归处理右节点
    }
}

👻方法2：遍历法（BFS）

思路分析：通过BFS、DFS遍历节点，然后进行计数统计

/**
 * 🟢222 完全二叉树的节点个数
 */
public class Solution222_02 {

    // 迭代法：基于遍历的思路，计算节点值
    public int countNodes(TreeNode root) {
        if (root == null) {
            return 0;
        }
        return bfs(root);
    }

    public int bfs(TreeNode node) {
        // 递归出口
        if (node == null) {
            return 0;
        }

        int nodeSize = 0; // 统计节点个数

        // 构建队列辅助遍历
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(node);// 初始化队列
        while (!queue.isEmpty()) {
            TreeNode cur = queue.poll();
            nodeSize++;
            // 处理子节点
            if (cur.left != null) {
                queue.offer(cur.left);
            }
            if (cur.right != null) {
                queue.offer(cur.right);
            }
        }
        // 返回统计结果
        return nodeSize;
    }
}

👻方法3：分类计数法（递归计算区分满二叉树和普通二叉树的处理）

思路分析：基于对上述DFS算法的递归优化改造，计算前会判断当前节点的子树是否为满二叉树（如果是可以直接通过公式计算，如果不是则通过递归方式计算）
- ① 满二叉树判断：如果最左和最右的深度一样，则说明该完全二叉树是满二叉树（此处充分利用完全二叉树的特点）
- ② 递归优化：也就是说在递归的过程中，会先判断当前节点的子树是否为满二叉树（如果是可以直接通过公式计算得到节点个数，如果不是则继续通过递归方式计算），优化原遍历O（n）时间复杂度

/**
 * 完全二叉树的节点个数（222）
 */
public class Solution2 {

    public int countNodes(TreeNode root) {
        if (root == null) {
            return 0;
        }
        return dfs(root);
    }

    public int dfs(TreeNode node) {
        if (node == null) {
            return 0;
        }

        // 判断当前节点的子树（完全二叉树）是否为满二叉树，如果是则无需递归，可通过公式计算
        int leftDepth = 0;
        TreeNode curLeft = node.left;
        while (curLeft != null) {
            leftDepth++;
            curLeft = curLeft.left; // 向左
        }

        int rightDepth = 0;
        TreeNode curRight = node.right;
        while (curRight != null) {
            rightDepth++;
            curRight = curRight.right; // 向右
        }

        // ① 如果leftDepth==rightDepth，则说明当前子树为满二叉树，直接通过公式计算返回节点个数
        if (leftDepth == rightDepth) {
            return (2 << leftDepth) - 1; // 注意(2<<1) 相当于2^2，所以leftDepth初始为0
        }

        // ② 如果leftDepth!=rightDepth，则通过递归方式计算节点个数
        int leftCnt = dfs(node.left);
        int rightCnt = dfs(node.right);
        return leftCnt + rightCnt + 1;
    }

}

复杂度分析
- 时间复杂度：
- 空间复杂度：

🟢平衡二叉树（110）

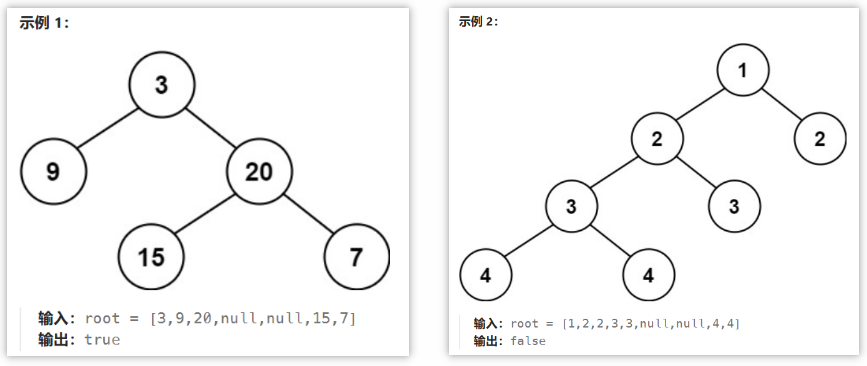
1.题目内容open in new window

给定一个二叉树，判断它是否是平衡二叉树

2.题解思路

【1】自顶向下的递归：平衡二叉树特性（每个子树的最大高度差不超过1），遍历每个节点判断是否符合平衡二叉树特性，且其子节点也需符合平衡二叉树特性

👻方法1：自顶向下的递归（DFS）

平衡二叉树特性（每个子树的最大高度差不超过1）：一棵二叉树是平衡二叉树，当且仅当其所有子树也都是平衡二叉树，因此可以使用递归的方式判断二叉树是不是平衡二叉树，递归的顺序可以是自顶向下或者自底向上

思路分析：关注【平衡二叉树】的特性，每个子树的最大高度差不超过1
- 因此可以通过递归的方式判断每个子树节点的最大高度差是否不超过1，并递归判断当前节点的左右子树是否也满足平衡二叉树的特性。基于此可以看到此处涉及两个DFS的操作：
  - （1）求节点的最大深度（树的高度）
  - （2）自顶向下的递归：判断每个节点是否满足【平衡二叉树】特性

/**
 * 🟢110 平衡二叉树
 */
public class Solution110_01 {

    // DFS:平衡二叉树每个节点的左右子树高度差不超过1（超出1说明非平衡）
    public boolean isBalanced(TreeNode root) {
        return balance(root);
    }

    /**
     * 基于平衡二叉树的特性：核心思路是校验每个节点的左右子树的高度差是否大于1
     * 1.递归遍历每个节点，判断每个节点的左右子树的高度差是否大于1
     * 2.定义计算节点高度方法（即求节点的最大深度）
     */
    public boolean balance(TreeNode node) {
        if (node == null) {
            return true;
        }
        // 校验当前节点左右子树高度差是否大于1
        if (Math.abs(maxDepth(node.left) - maxDepth(node.right)) > 1) {
            return false;
        }
        // 继续递归校验
        return balance(node.left) && balance(node.right);
    }

    // 求节点的最大深度
    public int maxDepth(TreeNode node) {
        if (node == null) {
            return 0;
        }
        int leftMaxDepth = maxDepth(node.left);
        int rightMaxDepth = maxDepth(node.right);
        return Math.max(leftMaxDepth, rightMaxDepth) + 1;
    }
}

复杂度分析
- 时间复杂度：算法实现涉及两个部分：节点遍历O（n）+最大深度差值校验（最坏情况下链式结构，时间复杂度为O（n）），因此总时间复杂度为O（n²）
- 空间复杂度：O（n），n 是二叉树中的节点个数，空间复杂度主要取决于递归调用的层数，递归调用的层数不会超过 n

优化DFS(递归计算深度的过程中校验高度差)

/**
 * 🟢110 平衡二叉树
 */
public class Solution110_02 {

    // DFS:平衡二叉树每个节点的左右子树高度差不超过1（超出1说明非平衡）
    public boolean isBalanced(TreeNode root) {
        int validRes = depth(root);
        return validRes != -1; // 如果得到-1则说明树不平衡，否则返回的是正确的树高度
    }

    /**
     * 基于平衡二叉树的特性：核心思路是校验每个节点的左右子树的高度差是否大于1
     * 1.递归遍历每个节点，判断每个节点的左右子树的高度差是否大于1
     * 2.定义计算节点高度方法（即求节点的最大深度）
     * - 实际上上述涉及到两个递归调用的过程，可以考虑将其整理为1个递归过程，也就是说递归计算子树高度的同时判断高度差
     * 如果高度差大于1，则直接返回-1（一个执行的标识）（将-1逐步递归往上抛），如果遍历发现存在-1的高度说明不平衡则直接返回false
     */
    public int depth(TreeNode node) {
        if (node == null) {
            return 0;
        }
        // 计算左右子树的高度
        int leftDepth = depth(node.left);
        int rightDepth = depth(node.right);

        // 校验左右子树的高度是否有效（如果出现-1，说明出现了不平衡，则继续将其直接抛出）
        if (leftDepth == -1 || rightDepth == -1) {
            return -1;
        }

        // 校验当前节点左右子树高度差是否大于1（如果大于1则返回-1，用于标记当前子树不平衡）
        if (Math.abs(leftDepth - rightDepth) > 1) {
            return -1;
        }

        // 如果当前左右子树的高度有效，则继续返回正确的高度值
        return Math.max(leftDepth, rightDepth) + 1;
    }

}

🍚04-路径篇（遍历、回溯问题）

🚀路径相关解题技巧

【1】BFS（广度优先遍历）+ 双队列：通过BFS+双队列的模式，同步记录遍历到每个节点对应的路径信息，确保节点的操作是同步的，当遇到指定条件例如遍历到子节点的时候则需要将当前的路径信息同步记录到结果集
【2】DFS（迭代 DLR）+ 双栈：这种思路实际和第1种解题思路是差不多的，通过维护双集合同步记录数据，满足条件则输出
【3】DFS（递归）（+ 回溯）：这种思路主要是确定好递归三要素（递归参数和返回类型、递归出口、递归过程），以及对递归顺序的选择（DLR、LDR、LRD）
- （1）确定递归函数的参数和返回类型
  - 参数选择
    - 二叉树的根节点TreeNode node
    - 对于路径遍历，此处看递归处理过程中是否会用到path信息，用到则递归传入
    - 对于一些对整个过程都需要用到的参数（例如结果集的存储res），可以将其设置为全局参数，这样代码看起来条理更加清晰一些（而不需要再递归过程中传入）
  - 返回类型
    - 如果需要搜索整棵二叉树而不用处理递归值，则递归函数不需要返回值（参考113 路径总和II）
    - 如果需要搜索整棵二叉树且需要处理递归值，则递归函数需要返回值（参考236 二叉树的最近公共祖先）
    - 如果搜索其中一条符合条件的路径（找到就退出的情况）那么需要返回值（遇到满足的就及时退出）（参考112 路径总和）
- （2）确定终止条件
  - 确定递归的终止条件，遇到什么情况下会退出或者不需要处理。参考DFS思路（遇到叶子节点等情况，还有一些特例判断等）
    - 【112 路径总和】中不是通过累加路径和的方式进行计算的，而是通过递归递减的方式来检索，每次递归减去当前的节点值val，如果遍历到叶子节点则校验当前剩余的值是否和叶子节点的val匹配，如果匹配说明路径满足直接退出，不匹配则继续找
- （3）确定递归过程
  - 确定单层递归的逻辑
    - 【112 路径总和】是为了遍历到叶子节点进行判断，因此采用DLR的思路会不断递归到其左右节点直到叶子结点

🟢二叉树的所有路径（257）

1.题目内容open in new window

给你一个二叉树的根节点 root ，按 任意顺序 ，返回所有从根节点到叶子节点的路径。

叶子节点 是指没有子节点的节点。

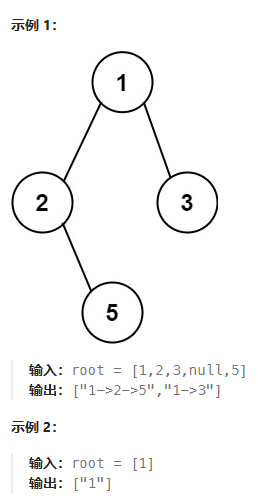
2.题解思路

思路分析：遍历+同步记录路径信息，遇到叶子节点说明可更新到res，遇到非叶子节点则相应同步记录path

【1】BFS + 双队列
【2】DFS 迭代（前序） + 双栈
【3】DFS 递归（DLR）
【4】DFS 递归（DLR） + 回溯

👻方法1：BFS + 双队列

思路分析：基于BFS广度优先遍历的思路，通过定义双队列维护遍历节点和遍历节点对应的路径（两者是同步维护的）
- nodeQueue 节点队列（用于辅助节点遍历）、pathQueue 路径队列（记录当前已遍历节点的路径，与nodeQueue对照）
- BFS 广度优先遍历：从nodeQueue 取出节点node的同时，从pathQueue 中取出以该节点结尾的路径curPath
  - 如果当前节点的左、右子节点都为null，说明当前节点是叶子节点，直接记录路径结果（即res.add(curPath)）
  - 如果当前节点的左、右子节点不为null，则将其子节点加入nodeQueue并同步更新路径信息到curPath（每次取出、插入操作确保两个队列操作是同步的，基于此队列的内容才是对照的（节点<=>当前节点的路径信息））

/**
 * 257 二叉树的所有路径
 */
public class Solution2 {

    /**
     * 层序遍历思路：nodeQueue 节点队列（用于辅助节点遍历）、pathQueue 路径队列（记录当前已遍历节点的路径，与nodeQueue对照）
     * 遍历每一层节点时，将当前节点与上一层节点的序列进行拼接，然后入队
     */
    public List<String> binaryTreePaths(TreeNode root) {
        // root 为null 判断
        if (root == null) {
            return new ArrayList<>();
        }

        // 定义路径结果集合
        List<String> res = new ArrayList<>();

        // 定义nodeQueue节点队列（用于辅助节点遍历）
        Deque<TreeNode> nodeQueue = new LinkedList<>();
        nodeQueue.offer(root);

        // 定义pathQueue路径队列（对应记录节点的路径信息，与nodeQueue对照）
        Deque<String> pathQueue = new LinkedList<>();
        pathQueue.offer(String.valueOf(root.val));

        // 遍历节点队列，同步更新路径信息
        while (!nodeQueue.isEmpty()) {
            // 同步取出节点
            TreeNode cur = nodeQueue.poll();
            String curPath = pathQueue.poll();

            // 遇到叶子节点则更新结果
            if (cur.left == null && cur.right == null) {
                res.add(curPath);
            }

            // 非叶子节点则继续遍历并同步更新路径
            if (cur.left != null) {
                nodeQueue.offer(cur.left);
                pathQueue.offer(curPath + "->" + cur.left);
            }
            if (cur.right != null) {
                nodeQueue.offer(cur.right);
                pathQueue.offer(curPath + "->" + cur.right);
            }
        }
        // 返回结果集
        return res;
    }
}

复杂度分析
- 时间复杂度：O（n）n 为树节点个数
空间复杂度：O（n）需要构建两个辅助队列操作

👻方法2：DFS 迭代 + 双栈

class Solution {
    /**
     * 迭代法
     */
    public List<String> binaryTreePaths(TreeNode root) {
        List<String> result = new ArrayList<>();
        if (root == null)
            return result;
        Stack<Object> stack = new Stack<>();
        // 节点和路径同时入栈
        stack.push(root);
        stack.push(root.val + "");
        while (!stack.isEmpty()) {
            // 节点和路径同时出栈
            String path = (String) stack.pop();
            TreeNode node = (TreeNode) stack.pop();
            // 若找到叶子节点
            if (node.left == null && node.right == null) {
                result.add(path);
            }
            //右子节点不为空
            if (node.right != null) {
                stack.push(node.right);
                stack.push(path + "->" + node.right.val);
            }
            //左子节点不为空
            if (node.left != null) {
                stack.push(node.left);
                stack.push(path + "->" + node.left.val);
            }
        }
        return result;
    }
}

复杂度分析
- 时间复杂度：
- 空间复杂度：

👻方法3：DFS 递归（DLR）

思路分析：基于DFS（DLR）的思路进行节点遍历，同步更新path的值列表（此处注意如果使用的是List要注意引用带来的影响，同理如果使用StringBuffer存储curPath也要注意对象引用问题）

/**
 * 257 二叉树的所有路径
 */
public class Solution3 {

    /**
     * DFS 思路：类似地，遍历节点的同时 同步 更新路径信息
     */
    public List<String> binaryTreePaths(TreeNode root) {
        if(root==null){
            return new ArrayList<>();
        }
        // 定义结果集，记录所有路径
        List<String> res = new ArrayList<>();
        List<String> curPath = new ArrayList<>();
        dfs(root,res,curPath);
        return res;
    }

    // DFS (DLR)
    public void dfs(TreeNode node,List<String> res,List<String> curPath){
        // 递归出口
        if(node==null){
            return;
        }

        // node 不为null，记录路径信息并继续递归遍历
        curPath.add(String.valueOf(node.val));

        // 如果左、右子节点都为null，说明是叶子节点，同步更新路径信息
        if(node.left==null && node.right==null){
            res.add(String.join("->",curPath));
        }else{
            // 如果子节点不为null，继续递归遍历子节点
            dfs(node.left,res,new ArrayList<>(curPath)); // 此处递归传入new一个对象，避免引用同一个对象导致问题
            dfs(node.right,res,new ArrayList<>(curPath));
        }
    }
}

复杂度分析
- 时间复杂度：
- 空间复杂度：

DFS（DLR）：dfs(TreeNode node,List<String> res,String curPath)版本
此处用String存储curPath，字符串拼接构建都是new的对象，所以不会出现上述引用问题（此处所谓的引用问题是这里用同一个对象进行了两次dfs调用，对象元素的修改会关联，而此处curPath的设定本身就是希望传入的是未修改前的内容，而不是经过递归后联动变更的数据）

/**
 * 257 二叉树的所有路径
 */
public class Solution4 {

    /**
     * DFS 思路：类似地，遍历节点的同时 同步 更新路径信息
     */
    public List<String> binaryTreePaths(TreeNode root) {
        if (root == null) {
            return new ArrayList<>();
        }
        // 定义结果集，记录所有路径
        List<String> res = new ArrayList<>();
        dfs(root, res, "");
        return res;
    }

    // DFS (DLR)
    public void dfs(TreeNode node, List<String> res, String curPath) {
        // 递归出口
        if (node == null) {
            return;
        }

        // node 不为null，记录路径信息并继续递归遍历
        curPath = curPath + node.val;

        // 如果左、右子节点都为null，说明是叶子节点，同步更新路径信息
        if (node.left == null && node.right == null) {
            res.add(String.join("->", curPath));
        } else {
            curPath = curPath + "->"; // 分隔符
            // 如果子节点不为null，继续递归遍历子节点
            dfs(node.left, res, curPath);
            dfs(node.right, res, curPath);
        }
    }
}

👻方法4：DFS递归（DLR） + 回溯

思路分析：和【方法2】中的实现思路是类似的，只不过此处在递归的时候用到了回溯思想，且需注意递归和回溯应为一个整体，需要放在同一个条件场景下，否则无法明确递归是否对curPath存在影响就无脑回溯则会导致错误

/**
 * 257 二叉树的所有路径
 */
public class Solution1 {

    /**
     * DFS 思路：类似地，遍历节点的同时 同步 更新路径信息
     */
    public List<String> binaryTreePaths(TreeNode root) {
        if (root == null) {
            return new ArrayList<>();
        }
        // 定义结果集，记录所有路径
        List<String> res = new ArrayList<>();
        List<String> curPath = new ArrayList<>();
        dfs(root, res, curPath);
        return res;
    }

    // DFS (DLR)
    public void dfs(TreeNode node, List<String> res, List<String> curPath) {
        // 递归出口
        if (node == null) {
            return;
        }

        // node 不为null，记录路径信息并继续递归遍历
        curPath.add(String.valueOf(node.val));

        // 如果左、右子节点都为null，说明是叶子节点，同步更新路径信息
        if (node.left == null && node.right == null) {
            res.add(String.join("->", curPath));
        } else {
            // 如果子节点不为null，继续递归遍历子节点(需分别调用两次dfs，因此此处要处理回溯)
            if (node.left != null) {
                dfs(node.left, res, curPath);
                curPath.remove(curPath.size() - 1); // 回溯：移除刚加入的最后一个元素
            }
            if (node.right != null) {
                dfs(node.right, res, curPath);
                curPath.remove(curPath.size() - 1); // 回溯：移除刚加入的最后一个元素
            }
        }
    }
}

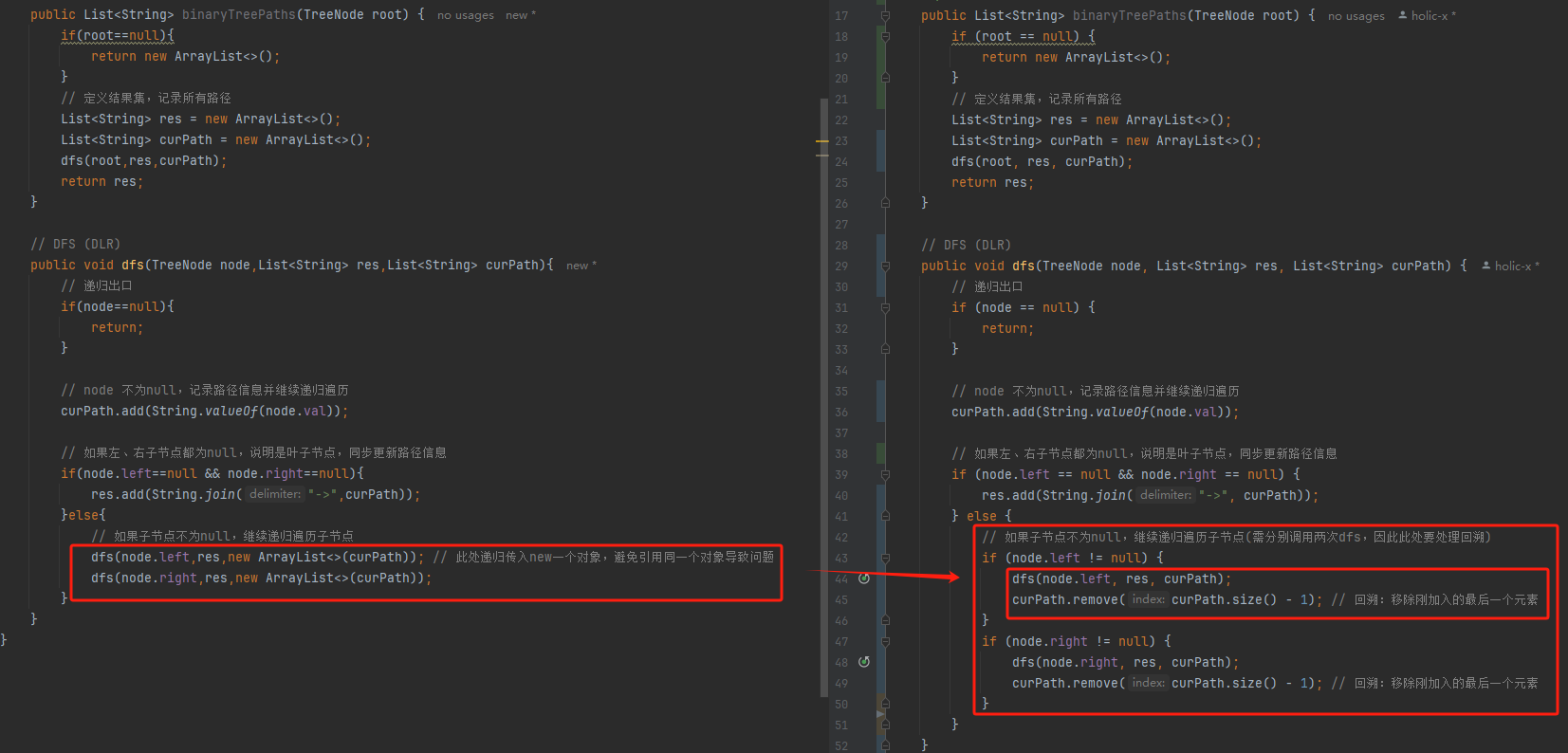
常见误区：下述语句是错误的回溯方式，此处回溯的目的是为了消除上一层递归带来的影响，如果说第1个dfs没有对curPath操作的话，则紧随其后的回溯语句就是多此一举的操作，进而导致错误。因此一定要确保递归和回溯操作的整体性

dfs(node.left,res,new ArrayList<>(curPath)); // 此处递归传入new一个对象，避免引用同一个对象导致问题
curPath.remove(curPath.size() - 1); // 回溯：移除刚加入的最后一个元素
dfs(node.right,res,new ArrayList<>(curPath));
curPath.remove(curPath.size() - 1); // 回溯：移除刚加入的最后一个元素

回溯的另一种写法参考

/**
 * 🟢 257 二叉树的所有路径
 * 路径输出格式：["1->2->5","1->3"]
 */
public class Solution257_02 {

    public List<String> res = new ArrayList<>(); // 记录结果
    public List<String> path = new ArrayList<>(); // 记录遍历路径(处理为节点)

    // DFS
    public List<String> binaryTreePaths(TreeNode root) {
        if (root == null) {
            return new ArrayList<>();
        }
        // 初始化将root加入路径
        path.add(String.valueOf(root.val));
        // 调用BFS算法获取路径
        dfs(root);
        return res;
    }

    // DFS(回溯思路)
    public void dfs(TreeNode node) {
        if (node == null) {
            return;
        }
        // 遇到叶子结点则记录结果集
        if (node.left == null && node.right == null) {
            res.add(String.join("->", path));
        }
        // 处理左右节点
        if (node.left != null) {
            path.add(String.valueOf(node.left.val));
            dfs(node.left);
            path.remove(path.size() - 1);
        }
        if (node.right != null) {
            path.add(String.valueOf(node.right.val));
            dfs(node.right);
            path.remove(path.size() - 1);
        }
    }
}

🟢路径总和（112）

1.题目内容open in new window

给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。

叶子节点 是指没有子节点的节点。

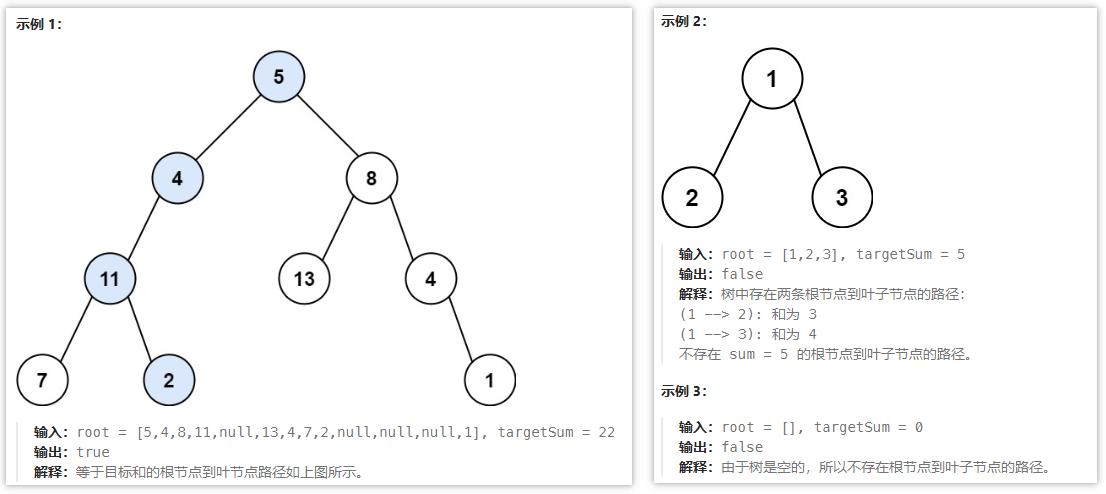
2.题解思路

👻方法1：层序遍历 + 双队列（参考【二叉树的所有路径思路】）

/**
 * 112 路径总和
 */
public class Solution1 {

    // 层序遍历+双队列：参考【所有路径】的思路（只不过此处存储的不是路径信息，而是路径之和数据）
    public boolean hasPathSum(TreeNode root, int targetSum) {
        if (root == null) {
            return false;
        }

        Deque<TreeNode> nodeQueue = new LinkedList<>();
        nodeQueue.offer(root);

        Deque<Integer> pathSumQueue = new LinkedList<>();
        pathSumQueue.offer(root.val);

        // 遍历节点，同步更新路径和
        while (!nodeQueue.isEmpty()) {
            TreeNode cur = nodeQueue.poll();
            int curPathSum = pathSumQueue.poll();

            // 判断当前节点是否为叶子节点（如果叶子节点，则说明已构成一条路径，需判断路径和是否与target匹配）
            if (cur.left == null && cur.right == null) {
                if (curPathSum == targetSum) {
                    return true;
                }
            }

            // 存在左右子节点则继续入队，并同步更新路径和
            if (cur.left != null) {
                nodeQueue.offer(cur.left);
                pathSumQueue.offer(curPathSum + cur.left.val);
            }
            if (cur.right != null) {
                nodeQueue.offer(cur.right);
                pathSumQueue.offer(curPathSum + cur.right.val);
            }

        }

        // 节点遍历完成，没找到匹配数据
        return false;
    }
}

复杂度分析
- 时间复杂度：
- 空间复杂度：

👻方法2：DFS

思路分析：将寻找路径和转化为递归到叶子节点判断剩余的值和叶子节点值是否一致
- 递归节点的过程中用targetSum减去当前的节点值，如果遇到叶子节点（如果路径和匹配targetSum，则递归最终到叶子节点剩余值应该和当前遍历节点值一致才满足）

/**
 * 112 路径总和
 */
public class Solution2 {

    // 递归法
    public boolean hasPathSum(TreeNode root, int targetSum) {
        return dfs(root, targetSum);
    }

    public boolean dfs(TreeNode node, int targetSum) {
        if (node == null) {
            return false;
        }

        // 遇到叶子节点（如果路径和匹配targetSum，则递归最终到叶子节点剩余值应该和当前遍历节点值一致才满足）
        if (node.left == null && node.right == null) {
            if (node.val == targetSum) {
                return true;
            }
        }

        // 左、右节点存在满足条件的即可
        return dfs(node.left, targetSum - node.val) || dfs(node.right, targetSum - node.val);
    }

}

复杂度分析
- 时间复杂度：
- 空间复杂度：

DFS 递归 + 回溯的写法

/**
 * 112 路径总和
 */
public class Solution3 {

    // DFS 递归 + 回溯
    public boolean hasPathSum(TreeNode root, int targetSum) {
        return dfs(root, targetSum);
    }

    public boolean dfs(TreeNode node, int targetSum) {
        if (node == null) {
            return false;
        }

        // 遇到叶子节点（如果路径和匹配targetSum，则递归最终到叶子节点剩余值应该和当前遍历节点值一致才满足）
        if (node.left == null && node.right == null) {
            if (node.val == targetSum) {
                return true;
            }
        }

        // 递归判断左、右节点是否满足条件
        if (node.left != null) {
            targetSum = targetSum - node.val; // 递归，处理节点
            if (dfs(node.left, targetSum)) {
                return true;
            }
            targetSum = targetSum + node.val; // 回溯（复原现场）
        }
        if (node.right != null) {
            targetSum = targetSum - node.val; // 递归，处理节点
            if (dfs(node.right, targetSum)) {
                return true;
            }
            targetSum = targetSum + node.val; // 回溯（复原现场）
        }

        // 没有满足条件的内容
        return false;
    }

}

/**
 * 🟢112 路径之和
 */
public class Solution112_03 {

    public int pathSum = 0;

    // DFS + 回溯
    public boolean hasPathSum(TreeNode root, int targetSum) {
        if (root == null) {
            return false;
        }
        // 初始化根节点加入路径
        pathSum += root.val;
        return dfs(root, targetSum);
    }

    public boolean dfs(TreeNode node, int targetSum) {
        if (node == null) {
            return false;
        }

        // 判断当前叶子结点值是否和targetSum一致
        if (node.left == null && node.right == null) {
            if (pathSum == targetSum) {
                return true;
            }
        }

        // 递归 + 回溯
        boolean validLeft = false, validRight = false;
        if (node.left != null) {
            pathSum += node.left.val;
            validLeft = dfs(node.left, targetSum);
            pathSum -= node.left.val;
        }
        if (node.right != null) {
            pathSum += node.right.val;
            validRight = dfs(node.right, targetSum);
            pathSum -= node.right.val;
        }
        // 左、右节点找到一条满足的路径即可
        return validLeft || validRight;
    }
}

🟡路径总和II（113）

1 .题目内容open in new window

给你二叉树的根节点 root 和一个整数目标和 targetSum ，找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。

叶子节点 是指没有子节点的节点。

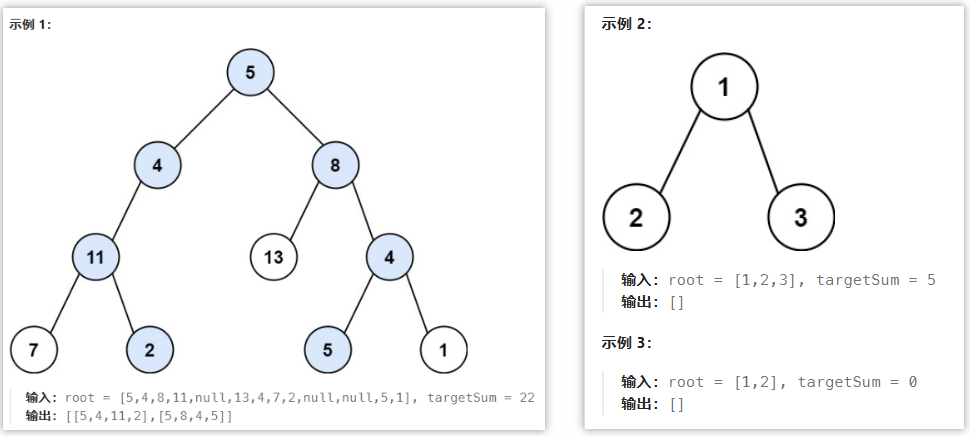
2.题解思路

👻方法1：BFS + 双队列 + 回溯

思路分析：BFS + 双队列 + 回溯，遍历节点的同时同步记录当前节点的路径和（及路径信息），遇到叶子结点则判断路径和是否和target一致，一致则加入结果集，直到所有节点遍历完成

/**
 * 113 路径总和II
 */
public class Solution1 {

    /**
     * BFS + 双队列
     */
    public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
        if (root == null) {
            return new ArrayList<>();
        }

        // 定义路径结果集合
        List<List<Integer>> res = new ArrayList<>();

        Deque<TreeNode> nodeQueue = new LinkedList<>(); // 节点队列
        nodeQueue.offer(root);

        Deque<Integer> pathSumQueue = new LinkedList<>(); // 路径和队列
        pathSumQueue.offer(root.val);

        Deque<List<Integer>> pathQueue = new LinkedList<>(); // 路径信息队列（记录完整路径）
        List<Integer> path = new ArrayList<>();
        path.add(root.val);
        pathQueue.offer(path);

        // 遍历节点，同步更新路径和并校验叶子结点处的targetSum是否匹配
        while (!nodeQueue.isEmpty()) {
            TreeNode cur = nodeQueue.poll();
            int curPathSum = pathSumQueue.poll();
            List<Integer> curPath = pathQueue.poll();

            // 校验targetSum是否匹配（叶子结点处校验）
            if (cur.left == null && cur.right == null) {
                if (curPathSum == targetSum) {
                    // 将当前路径信息更新到结果集
                    res.add(new ArrayList<>(curPath));
                }
            }

            // 如果左右子节点不为空，则继续入队
            if (cur.left != null) {
                nodeQueue.offer(cur.left); // 1.左节点入队
                pathSumQueue.offer(curPathSum + cur.left.val); // 2.同步更新对应路径和
                // 3.同步更新对应路径信息
                curPath.add(cur.left.val);
                pathQueue.offer(new ArrayList<>(curPath)); // 此处是new一个新的集合并将元素封装过去，避免引用影响
                curPath.remove(curPath.size() - 1); // 回溯：复原现场
            }
            if (cur.right != null) {
                nodeQueue.offer(cur.right); // 1.右节点入队
                pathSumQueue.offer(curPathSum + cur.right.val); // 2.同步更新对应路径和
                // 3.同步更新对应路径信息
                curPath.add(cur.right.val);
                pathQueue.offer(new ArrayList<>(curPath)); // 此处是new一个新的集合并将元素封装过去，避免引用影响
                curPath.remove(curPath.size() - 1); // 回溯：复原现场
            }
        }

        // 遍历结束，返回结果集
        return res;
    }

}

复杂度分析
- 时间复杂度：
- 空间复杂度：

👻方法2：DFS + 回溯

思路分析：基于DFS思路进行遍历。需注意此处要先更新路径信息，再判断叶子节点（不同于112 路径总和中判断的targetSum和叶子节点值相等这一步就可以，因为其只需要判断路径是否存在，而此处的题目要求是求出完整路径，因此要先更新完整路径信息）

/**
 * 113 路径总和II
 */
public class Solution2 {

    List<List<Integer>> res = new ArrayList<>(); // 结果集
    List<Integer> path = new ArrayList<>(); // 当前遍历路径

    /**
     * DFS + 回溯
     */
    public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
        if (root == null) {
            return new ArrayList<>();
        }

        // 调用递归
        dfs(root, targetSum);
        return res;
    }

    // DFS（DLR） + 回溯：递归获取路径，递归过程中需要处理【路径信息】和【路径和信息】
    public void dfs(TreeNode node, int targetSum) {
        // 递归出口
        if (node == null) {
            return;
        }

        // 先更新完整路径
        targetSum = targetSum - node.val;
        path.add(node.val);

        // 判断当前路径是否匹配
        if (node.left == null && node.right == null) {
            // 判断叶子节点所在路径是否匹配
            if (targetSum == 0) { // 递减剩余值为0，则说明存在路径
                res.add(new ArrayList<>(path));
            }
        }

        // 执行递归
        dfs(node.left, targetSum);
        // 执行递归
        dfs(node.right, targetSum);
        // 回溯：复原递归参数
        path.remove(path.size() - 1);
    }

}

复杂度分析
- 时间复杂度：
- 空间复杂度：

🍚05-二叉树的属性

🟢左叶子之和（404）

1.题目内容open in new window

给定二叉树的根节点 root ，返回所有左叶子之和

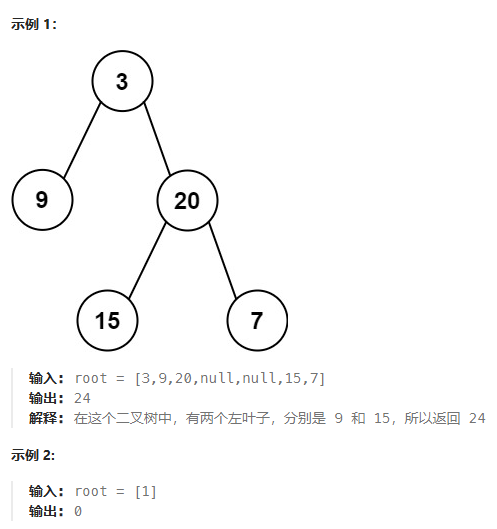
2.题解思路

核心思路：理解左叶子的概念：如果一个节点存在左叶子，则其满足该节点的左节点不为null，且其左节点的左右子节点都为null

👻方法1：层序遍历

思路分析：基于层序遍历，遍历每个节点，然后判断当前节点是否存在左叶子（左节点不为null且左节点的左右子节点都为null），如果存在则进行左叶子节点值累加
易错点：此处容易理解为统计每层的第1个叶子节点元素和（左叶子概念理解错误），基于当前节点进行判断，如果节点存在左叶子则应满足（cur.left!=null && cur.left.left==null && cur.left.right==null），即存在左叶子的概念为存在左节点 + 该左节点为叶子节点

/**
 * 404 左叶子之和
 */
public class Solution1 {

    // 层序遍历：寻找左叶子
    public int sumOfLeftLeaves(TreeNode root) {
        if (root == null) {
            return 0;
        }

        // 记录左叶子累加值
        int leftSum = 0;

        Deque<TreeNode> queue = new LinkedList<>();
        queue.offer(root);

        while (!queue.isEmpty()) {
            TreeNode cur = queue.poll();

            // 判断左叶子(遍历当前节点，判断其是否有左叶子：左节点不为空，左节点的左右子节点为空)
            if (cur.left != null && cur.left.left == null && cur.left.right == null) {
                leftSum += cur.left.val; // 左叶子节点值累加
            }

            // 左、右子节点不为空则入队
            if (cur.left != null) {
                queue.offer(cur.left);
            }
            if (cur.right != null) {
                queue.offer(cur.right);
            }
        }

        // 返回结果
        return leftSum;
    }
}

复杂度分析
- 时间复杂度：O（n）n为树中所有节点的个数
- 空间复杂度：O（n）构建队列辅助遍历，而队列的大小取决于每层的最大节点个数

👻方法2：DFS（DLR）

思路分析：基于DLR思路递归遍历二叉树，随后判断是否存在左叶子，存在则进行累加
- 此处leftSum是全局遍历，因此将它单独拉出来放在全局遍历定义，避免递归过程中传来传去

/**
 * 404 左叶子之和
 */
public class Solution2 {

    int leftSum = 0;

    // DFS 思路
    public int sumOfLeftLeaves(TreeNode root) {
        if (root == null) {
            return 0;
        }
        dfs(root);
        return leftSum;
    }

    // DFS(DLR)
    public void dfs(TreeNode node) {
        if (node == null) {
            return;
        }

        // 判断当前节点是否存在"左叶子"
        if (node.left != null && node.left.left == null && node.left.right == null) {
            // 存在左叶子：累加和
            leftSum += node.left.val;
        }

        // 递归遍历左右子节点
        dfs(node.left);
        dfs(node.right);
    }
}

复杂度分析
- 时间复杂度：O（n）n为树中所有节点的个数
- 空间复杂度：取决于栈的深度

/**
 * 404 左叶子之和
 */
public class Solution3 {

    // DFS 思路
    public int sumOfLeftLeaves(TreeNode root) {
        if (root == null) {
            return 0;
        }
        return dfs(root);
    }

    // DFS(DLR)
    public int dfs(TreeNode node) {
        if (node == null) {
            return 0;
        }

        int leftSum = 0;
        // 判断当前节点是否存在"左叶子"
        if (node.left != null && node.left.left == null && node.left.right == null) {
            // 存在左叶子：累加和
            leftSum = node.left.val;
        }

        return leftSum + dfs(node.left) + dfs(node.right);
    }
}

🟡找树左下角的值（513）

1.题目内容open in new window

给定一个二叉树的 根节点 root，请找出该二叉树的 最底层最左边 节点的值。

假设二叉树中至少有一个节点。

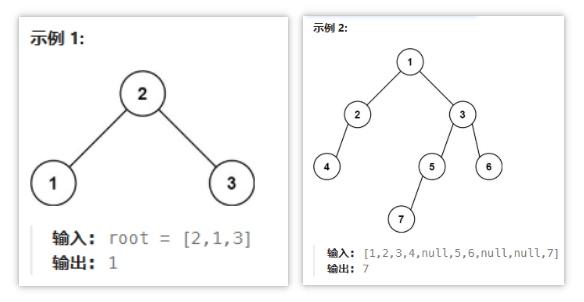
2.题解思路

核心思路：
- 【1】层序遍历（需遍历完所有元素才能知道是不是最左下角，因此不要局限于找到就能退出的思路，而是要遍历所有节点才能确定），两种方式都定义了target辅助存储中间过程的遍历元素
  - 思路1【自上而下，从左到右】：返回最后一层的第1个元素
  - 思路2【自上而下，从右到左】：最后出队的元素即为最底层最左边节点的值（🚀推荐，不需要额外分层）
- 【2】递归
  - DFS思路：在第1次出现"跳层"的情况下更新target(对于同层而言level都是相同的，但是如果跳到下一层则需要同步更新level和target，判断当前level和最大level的值是否相同，相同则说明同层，不同则说明level更新了，则在第一次更新的时候同步更新maxLevel和target)

👻方法1：BFS（层序遍历）

【1】层序遍历（需基于层序遍历所有节点，更新查找的目标值target，对于不同的遍历思路，target的定位不同）

思路1【自上而下，从左到右】：返回最后一层的第1个元素（用target存储每一层的第一个元素（可根据下标定位））

/**
 * 🟡513 找树左下角的值
 */
public class Solution513_01 {

    // 层序遍历：自顶向下，从左到右（找最后一层的第1个元素：分层）
    public int findBottomLeftValue(TreeNode root) {
        if (root == null) {
            return 0;
        }
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);

        int target = 0; // target 用于存储每一层的第1个元素
        while (!queue.isEmpty()) {
            // 分层遍历
            int cnt = queue.size();
            for (int i = 0; i < cnt; i++) {
                TreeNode cur = queue.poll();
                if (i == 0) {
                    target = cur.val; // target 用于记录每一层的第1个元素
                }
                if (cur.left != null) {
                    queue.offer(cur.left);
                }
                if (cur.right != null) {
                    queue.offer(cur.right);
                }
            }
        }

        // 返回结果(当所有节点遍历完成，此时target指向遍历的最后一层的第1个元素)
        return target;
    }
}

思路2【自上而下，从右到左】：最后出队的元素即为最底层最左边节点的值（🚀推荐，不需要额外分层，此时target存储的是每个遍历元素，基于此遍历顺序最终遍历完成后target存储的是最后一个遍历元素）

/**
 * 513 找树左下角的值
 */
public class Solution1 {

    /**
     * 层序遍历
     * - 思路1【自上而下，从左到右】：返回最后一层的第1个元素
     * - 思路2【自上而下，从右到左】：最后出队的元素即为**最底层 最左边**节点的值（🚀推荐，不需要额外分层）
     */
    public int findBottomLeftValue(TreeNode root) {
        if(root==null){
            return 0;
        }

        int target = 0;

        Deque<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        while(!queue.isEmpty()){
            TreeNode cur = queue.poll();
            target = cur.val; // 更新target
            // 自上而下、从右到左
            if(cur.right!=null){
                queue.offer(cur.right);
            }
            if(cur.left!=null){
                queue.offer(cur.left);
            }
        }
        return target; // 最后一个出队元素即为所得
    }
}

复杂度分析
- 时间复杂度：O（n）n为树中所有节点的个数
- 空间复杂度：O（n）构建队列辅助遍历，而队列的大小取决于每层的最大节点个数

👻方法2：DFS（深度优先遍历）

DFS（DLR）：记录当前遍历层数level和最大层数levelMax，如果level>levelMax则说明遍历到下一层的节点（始终是LR顺序：因此当level>levelMax第一次满足的时候直接更新levelMax和target的值即可，这个条件只有在第一次遍历新层的时候触发，因此可以确保target更新的时机是每一层的首个左节点）
- 涉及target（每1层的第1个元素，通过覆盖更新）、maxLevel（当前遍历的最大层数/深度）、curLevel（当前遍历深度）
DFS顺序选择：因为遍历顺序始终是LR因此此处不管是三种中的哪一种遍历顺序都可以，只关注深度的变化

/**
 * 513 找树左下角的值
 */
public class Solution2 {

    int levelMax = -1; // 当前遍历的最大层数
    int target = -1; // 目标元素

    /**
     * DFS：递归
     */
    public int findBottomLeftValue(TreeNode root) {
        if (root == null) {
            return 0;
        }
        // 递归
        dfs(root, 0);
        return target;
    }

    // DFS：DLR
    public void dfs(TreeNode node, int curLevel) {
        if (node == null) {
            return;
        }

        // 判断是否为新层，如果为新的一层则更新levelMax并更新target（每次遍历新层的第一个节点为当层的左节点）
        if (curLevel > levelMax) {
            levelMax = curLevel; // 更新当前最大层
            target = node.val;
        }

        // 递归左、右节点
        dfs(node.left, curLevel + 1);
        dfs(node.right, curLevel + 1);
    }
}

复杂度分析
- 时间复杂度：O（n）n为树中所有节点的个数
- 空间复杂度：取决于栈的深度

🟢合并二叉树（617）

1.题目内容open in new window

给你两棵二叉树： root1 和 root2 。

想象一下，当你将其中一棵覆盖到另一棵之上时，两棵树上的一些节点将会重叠（而另一些不会）。你需要将这两棵树合并成一棵新二叉树。合并的规则是：如果两个节点重叠，那么将这两个节点的值相加作为合并后节点的新值；否则，不为 null 的节点将直接作为新二叉树的节点。

返回合并后的二叉树。

注意: 合并过程必须从两个树的根节点开始。

2.题解思路

👻方法1：BFS（广度优先遍历） + 3队列

思路分析：双指针遍历，在原树上进行修改（NPE判断，值叠加）
- 条件判断：尽量避免拆开遍历和入队，不然各自要拆很多情况讨论。在讨论两棵树节点合并的情况的同时，遍历完成就将相应的左、右子节点入队
- （1）构建3个队列：queue1、queue2分别用于辅助遍历root1、root2，mergeQueue用于辅助新树的遍历（初始化存入根节点，在后序的迭代过程中取出节点构建左右节点）
- （2）同时遍历两个队列（循环条件是：两个遍历队列都不为空）此处之所以循环条件这样设计不考虑多出来的节点（某个队列遍历结束另一个队列还没结束）是因为在遍历过程中的处理（分为左节点处理、右节点处理）会分情况讨论
  - 如果两个节点都不为null，则构建新节点进行挂载
    - 创建新节点（两数之和），更新mergeNode的左/右节点。遍历完成，在此处将相应的左/右节点进行入队，等待继续下次遍历（此处将遍历和入队放在相应的判断条件中执行，不拆开是为了避免重复判断条件）
  - 如果两个节点中某一个节点为null，则会将非null的节点直接挂到mergeTree指定位置上（基于此相当于将整个子树都挂载过去了，因此循环条件才不需要考虑多出来的部分）
  - 如果两个节点都为null，不做任何操作（默认null）

/**
 * 617 合并二叉树
 */
public class Solution1 {

    public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
        // root1\root2 的 null 判断
        if (root1 == null) {
            return root2;
        }
        if (root2 == null) {
            return root1;
        }

        // 构建两个队列分别用于遍历root1、root2 树
        Deque<TreeNode> queue1 = new LinkedList<>();
        queue1.offer(root1);

        Deque<TreeNode> queue2 = new LinkedList<>();
        queue2.offer(root2);

        // 构建新队列存储新树节点
        Deque<TreeNode> mergeQueue = new LinkedList<>();
        TreeNode mergeRoot = new TreeNode(root1.val + root2.val);
        mergeQueue.offer(mergeRoot);


        /**
         * 同时遍历两棵树,如果其中一个队列为空则退出遍历
         * 此处之所以不考虑多出来的节点是因为在遍历过程中的处理（分为左节点处理、右节点处理）：
         * - 如果两个节点都不为null，则构建新节点进行挂载
         * - 如果两个节点中某一个节点为null，则会将非null的节点直接挂到mergeTree指定位置上
         * - 如果两个节点都为null，不做任何操作（默认null）
         */
        while (!queue1.isEmpty() && !queue2.isEmpty()) {

            // 同时取出队列中的节点进行遍历、合并
            TreeNode cur1 = queue1.poll();
            TreeNode cur2 = queue2.poll();
            TreeNode mergeNode = mergeQueue.poll();

            // 左节点、右节点判断
            TreeNode left1 = cur1.left, right1 = cur1.right;
            TreeNode left2 = cur2.left, right2 = cur2.right;

            // 判断当前遍历节点的左节点情况
            if (left1 != null && left2 != null) {
                // 两棵树的对应位置节点都不为空，需相加后构成新节点
                TreeNode mergeLeftNode = new TreeNode(left1.val + left2.val);
                mergeNode.left = mergeLeftNode;
                // 节点入队
                queue1.offer(left1);
                queue2.offer(left2);
                mergeQueue.offer(mergeLeftNode);

            } else if (left1 != null) {
                // left1 不为空，则选择挂载 left1
                mergeNode.left = left1;
            } else if (left2 != null) {
                // left2 不为空，则选择挂载 left2
                mergeNode.left = left2;
            }

            // 判断当前遍历节点的右节点情况
            if (right1 != null && right2 != null) {
                // 两棵树的对应位置节点都不为空，需相加后构成新节点
                TreeNode mergeLeftNode = new TreeNode(right1.val + right2.val);
                mergeNode.right = mergeLeftNode;

                // 节点入队
                queue1.offer(right1);
                queue2.offer(right2);
                mergeQueue.offer(mergeLeftNode);

            } else if (right1 != null) {
                // right1 不为空，则选择挂载 right1
                mergeNode.right = right1;
            } else if (right2 != null) {
                // right2 不为空，则选择挂载 right2
                mergeNode.right = right2;
            }
        }

        return mergeRoot;
    }

}

复杂度分析
- 时间复杂度：
- 空间复杂度：

单个队列+原队列修改：操作思路

class Solution4 {
    // 使用队列迭代
    public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
        if (root1 == null) return root2;
        if (root2 ==null) return root1;
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root1);
        queue.offer(root2);
        while (!queue.isEmpty()) {
            TreeNode node1 = queue.poll();
            TreeNode node2 = queue.poll();
            // 此时两个节点一定不为空，val相加
            node1.val = node1.val + node2.val;
            // 如果两棵树左节点都不为空，加入队列
            if (node1.left != null && node2.left != null) {
                queue.offer(node1.left);
                queue.offer(node2.left);
            }
            // 如果两棵树右节点都不为空，加入队列
            if (node1.right != null && node2.right != null) {
                queue.offer(node1.right);
                queue.offer(node2.right);
            }
            // 若node1的左节点为空，直接赋值
            if (node1.left == null && node2.left != null) {
                node1.left = node2.left;
            }
            // 若node1的右节点为空，直接赋值
            if (node1.right == null && node2.right != null) {
                node1.right = node2.right;
            }
        }
        return root1;
    }
}

👻方法2：DFS

思路分析：使用深度优先搜索合并两个二叉树。从根节点开始同时遍历两个二叉树，并将对应的节点进行合并
- 两个二叉树的对应节点可能存在以下三种情况，对于每种情况使用不同的合并方式
  - 如果两个二叉树的对应节点都为空，则合并后的二叉树的对应节点也为空；
  - 如果两个二叉树的对应节点只有一个为空，则合并后的二叉树的对应节点为其中的非空节点；
  - 如果两个二叉树的对应节点都不为空，则合并后的二叉树的对应节点的值为两个二叉树的对应节点的值之和，此时需要显性合并两个节点
  - 对一个节点进行合并之后，还要对该节点的左右子树分别进行合并（这是一个递归的过程）

/**
 * 617 合并二叉树
 */
public class Solution2 {

    public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
        return buildHelper(root1, root2);
    }

    public TreeNode buildHelper(TreeNode node1, TreeNode node2) {

        /**
         * 分三种情况讨论：
         * 1.node1、node2 都为null，合并后的节点也为null
         * 2.node1、node2 都不为null，合并后的节点是两个节点之和，相应需要递归构建左、右子节点
         * 3.node1、node2 其中一个为null，合并后的节点是不为null的那个(直接挂载)
         */
        // node1、node2 都为null
        if (node1 == null && node2 == null) {
            return null;
        }
        // node1为null，选择node2
        if (node1 == null) {
            return node2;
        }
        // node2为null，选择node1
        if (node2 == null) {
            return node1;
        }

        // node1、node2 都不为null，合并后的节点是两个节点之和，相应需要递归构建左、右子节点
        TreeNode mergeNode = new TreeNode(node1.val + node2.val);
        mergeNode.left = buildHelper(node1.left, node2.left);
        mergeNode.right = buildHelper(node1.right, node2.right);
        return mergeNode;
    }

}

复杂度分析
- 时间复杂度：
- 空间复杂度：

🍚06-二叉树的构建（二叉树、二叉搜索树）

🚀二叉树构建解题技巧

梳理序列的特点：
- DLR（前序遍历）：序列的第1个节点是root
- LDR（中序遍历）：已知root的情况下，以root为分界线可以拿到左右区间
- LRD（后序遍历）：序列的最后1个节点是root
二叉树的构建
- 【前序/后序 + 中序】的组合可以唯一构建一棵二叉树
- 【前序 + 后序】的组合由于无法明确左右部分（中序可以通过root进行左右区间划分）会存在二义性问题
易错点
- 区间取值：取闭区间，画图理解（看具体实现和初始化方法调用，不纠结），明确索引位置和有效范围
  - 分割时，坚持区间不变量原则（左闭右开 || 左闭右闭）
  - 分割时，注意后序或者前序已经有一个节点作为中间节点了，因此这个节点位置不能继续使用了
- 区间元素个数计算：[left,right]=> size = right - left + 1，因此当已知left和size，右区间right = left + size -1

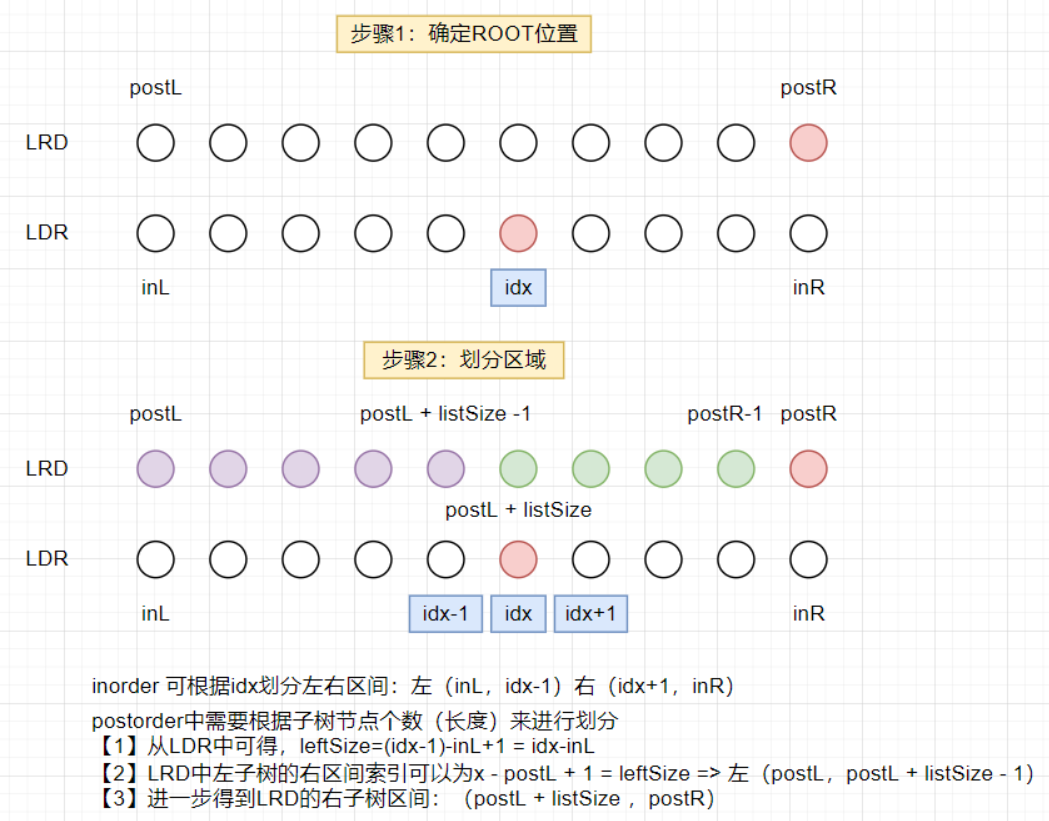
前序+中序二叉树构建思路（前序确定root（第1个）、中序确定root位置和区间元素个数）
- 前序preorder+中序inorder：初始化已知这两个序列的左右边界分别为[preL,preR]、[inL,inR]
- 构建根节点（前序序列特性）：序列的第1个节点为根节点，即root => preorder[preL]（此处都是取闭区间，直接根据索引位置构建即可；如果是开区间，自行注意取值）
- 构建左右区间（中序序列特性）：拿到root值，则可进一步在中序序列中确定根节点的索引位置，进而确定左右区间的元素个数取值
  - 中序：左区间[inL,idx-1]、根节点idx、右区间[idx+1,inR]
  - 前序：基于上述中序序列和根节点位置可以拿到左右区间各自的元素个数，基于此可以进一步根据前序序列的边界和元素个数敲定前序序列的**【中左右】**关系
    - 根节点preL，左区间[preL+1,preL+leftSize]（根据右边计算公式为(preL+1) + leftSize - 1），右区间[preL+leftSize+1,preR]
- 基于上述分析，则可构建buildHelper(int[] preorder, int[] inorder, int preL, int preR, int inL, int inR)方法，递归构建节点关系
  - 构建二叉树是基于前序序列进行构建的，因此此处递归出口校验索引范围是否有效（即[preL,preR]需有效，preL>preR时表示区间无效，直接返回null）
  - 依次构建root、root.left、root.right
  - 构建完成返回构建好的节点
- buildHelper构建完成，在主方法中直接初始化调用即可，注意传入闭区间
后序+中序二叉树构建思路（后序确定root（最后1个）、中序确定root位置和区间元素个数）
- 后序postorder+中序inorder：初始化已知这两个序列的左右边界分别为[postL,postR]、[inL,inR]
- 构建根节点（后序序列特性）：序列的最后1个节点为根节点，即root => postorder[postR]（此处都是取闭区间，直接根据索引位置构建即可）
- 构建左右区间（中序序列特性）：拿到root值，则可进一步在中序序列中确定根节点的索引位置，进而确定左右区间的元素个数取值
  - 中序：左区间[inL,idx-1]、根节点idx、右区间[idx+1,inR]
  - 前序：基于上述中序序列和根节点位置可以拿到左右区间各自的元素个数，基于此可以进一步根据前序序列的边界和元素个数敲定前序序列的**【左右中】**关系
    - 左区间[postL,postL+leftSize-1]（根据右边计算公式为postL + leftSize - 1），右区间[postL+leftSize,postR-1]，根节点postR
- 基于上述分析，则可构建buildHelper(int[] postorder, int[] inorder, int postL, int postR, int inL, int inR)方法，递归构建节点关系
  - 构建二叉树是基于后序序列进行构建的，因此此处递归出口校验索引范围是否有效（即[postL,postR]需有效，postL>postR时表示区间无效，直接返回null）
  - 依次构建root、root.left、root.right
  - 构建完成返回构建好的节点
- buildHelper构建完成，在主方法中直接初始化调用即可，注意传入闭区间

⚽ 普通数组与二叉树的转化

将一个普通数组转化为一棵二叉树（按照数组元素的先后顺序从上到下、从左到右依次填充二叉树（如果子节点为空则用null指代占位））。可以采用迭代、递归的方式实现：

迭代（借助辅助队列存储元素）：基于层次遍历的思路，每次取出当层元素，然后根据nums填充元素的左、右子节点后重新将其入队，等待下次循环取出遍历封装。此处需要注意的是节点为null的情况考虑（可以用一个不可能的val指代空节点（例如节点均为正整数，那么对于空节点可以用-1指代），也可对空节点进行特殊处理）

/**
 * 根据限定的一维数组构建树（如果叶子结点为空则用null占位） todo null 待完善
 */
public static TreeNode createBinaryTree(Integer[] nums) {
    int len = nums.length;
    if (len == 0) {
        return null;
    }

    // 借助队列辅助构建
    TreeNode root = new TreeNode(nums[0]);
    Queue<TreeNode> queue = new LinkedList();
    queue.offer(root);

    int idx = 1; // idx 指代当前遍历的nums元素位置
    while (!queue.isEmpty()) {
        int curSize = queue.size();
        for (int i = 0; i < curSize; i++) {
            // 取出元素，依次封装其左右子节点
            TreeNode node = queue.poll();
            if (node != null) {
                // 处理左节点
                if (idx >= len) {
                    break; // 如果元素全部遍历完成则直接跳出循环
                }
                node.left = new TreeNode(nums[idx] == null ? -1 : nums[idx]);
                idx++;

                // 处理右节点
                if (idx >= len) {
                    break; // 如果元素全部遍历完成则直接跳出循环
                }
                node.right = new TreeNode(nums[idx] == null ? -1 : nums[idx]);
                idx++;
            }

            // 将左右子节点分别入队
            queue.offer(node.left);
            queue.offer(node.right);
        }
    }

    // 返回构建好的树
    return root;
}

递归：此处需注意节点和数组元素下标的关系（递归处理）
- 数组下标和节点的对照关系：如果父节点在数组中的下标是i，则其左儿子在数组中对应的下标为2*i+1、其右儿子在数组中对应的下标为2*i+2

/**
* 递归构建树（dfs：DLR）
*/
public static TreeNode createBinaryTreeByDfs(Integer[] nums) {
    return createBinaryTreeHelper(nums, 0);
}

/**
* 递归构建树
*/
private static TreeNode createBinaryTreeHelper(Integer[] nums, int idx) {
    if (idx >= nums.length) {
        return null;
    }

    // 构建节点
    if (nums[idx] == null) {
        return null;
    }

    /**
    * 数组下标和节点的对照关系：如果父节点在数组中的下标是i，则其左儿子在数组中对应的下标为2*i+1、其右儿子在数组中对应的下标为2*i+2
    * 如果单纯用 idx++ 来切换节点对应下标元素位置，则在递归过程中会得到不正确的构建树
    */
    TreeNode node = new TreeNode(nums[idx]);
    node.left = createBinaryTreeHelper(nums, 2 * idx + 1);
    node.right = createBinaryTreeHelper(nums, 2 * idx + 2);

    // 返回构建的节点
    return node;
}

🟡从中序和前序遍历序列构造二叉树（105）

1.题目内容open in new window

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

2.题解思路

👻方法1：递归构造

/**
 * 105 从前序和中序遍历构造二叉树
 */
public class Solution1 {

    public TreeNode buildTree(int[] preorder, int[] inorder) {
        TreeNode node = buildHelper(preorder, inorder, 0, preorder.length - 1, 0, inorder.length - 1);
        return node;
    }

    /**
     * 辅助构造方法
     *
     * @param preorder 前序序列 指定构造索引范围 [preL,preR]
     * @param inorder  中序序列 指定构造索引范围 [inL,inR]
     */
    public TreeNode buildHelper(int[] preorder, int[] inorder, int preL, int preR, int inL, int inR) {

        // 基于前序序列进行构建
        if (preL > preR) {
            return null;
        }

        /**
         * 如果构建索引范围有效，则进行构建，取前序序列的第一个节点作为根节点进行构建
         * 中序：L[inL,idx-1]             R[preL+leftLen,idx - 1]
         * 前序：L[preL+leftLen+1,preR]   R[idx+1,inR]
         */
        TreeNode root = new TreeNode(preorder[preL]);

        // 得到当前root节点在中序遍历中的索引位置，并计算左区间的元素个数
        int idx = getInorderIdx(inorder, preorder[preL]);
        int leftLen = idx - inL; // [inL,idx-1]内的节点个数

        // 递归构建左、右子树
        root.left = buildHelper(preorder, inorder, preL + 1, preL + leftLen, inL, idx - 1);
        root.right = buildHelper(preorder, inorder, preL + leftLen + 1, preR, idx + 1, inR);

        // 返回构建的节点
        return root;
    }

    // 获取指定元素在中序序列中索引的位置
    public int getInorderIdx(int[] inorder, int target) {
        for (int i = 0; i < inorder.length; i++) {
            if (inorder[i] == target) {
                return i;
            }
        }
        return -1;
    }

}

复杂度分析
- 时间复杂度：
- 空间复杂度：

🟡从中序和后序遍历序列构造二叉树（106）

1.题目内容open in new window

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。

2.题解思路

👻方法1：递归构造

/**
 * 106 从前序和后序遍历构造二叉树
 */
public class Solution1 {

    public TreeNode buildTree(int[] inorder, int[] postorder) {
        TreeNode node = buildHelper(postorder, inorder, 0, postorder.length - 1, 0, inorder.length - 1);
        return node;
    }

    /**
     * @param postorder 后序序列 及构建范围 [postL,postR]
     * @param inorder   中序序列 及构建范围 [inL,inR]
     * @return
     */
    public TreeNode buildHelper(int[] postorder, int[] inorder, int postL, int postR, int inL, int inR) {

        // 基于后序序列进行构建
        if (postL > postR) {
            return null;
        }

        /**
         * 指定构建范围有效，则构建节点（后序序列的最后一个节点是root）
         * 中序：L[inL,idx-1]             R[idx+1,inR]
         * 后序：L[postL,postL+leftLen-1]   R[postL+leftLen,postR-1]
         */
        TreeNode root = new TreeNode(postorder[postR]);
        // 获取根节点在中序序列中的索引位置及左区间的元素个数
        int idx = getInorderIdx(inorder, postorder[postR]);
        int leftLen = idx - inL;

        // 递归构建左右子树
        root.left = buildHelper(postorder, inorder, postL, postL + leftLen - 1, inL, idx - 1);
        root.right = buildHelper(postorder, inorder, postL + leftLen, postR - 1, idx + 1, inR);

        // 返回构建的节点
        return root;
    }


    // 获取指定元素在中序序列中索引的位置
    public int getInorderIdx(int[] inorder, int target) {
        for (int i = 0; i < inorder.length; i++) {
            if (inorder[i] == target) {
                return i;
            }
        }
        return -1;
    }
}

复杂度分析
- 时间复杂度：
- 空间复杂度：

🟡最大二叉树（654）

1.题目内容open in new window

给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建：

创建一个根节点，其值为 nums 中的最大值。
递归地在最大值左边的 子数组前缀上 构建左子树。
递归地在最大值右边的 子数组后缀上 构建右子树。

返回 nums 构建的 最大二叉树 。

2.题解思路

参照上述根据前序/后序+中序的思路进行递归构建（一般是基于前序构建，在原数组上划分区间，敲定中、左、右的索引范围）

root：根节点是当前指定区间的最大值max，根据max所在位置maxIdx划分左右区间（maxIdx左侧为左区间、maxIdx右侧为右区间）
root.left：根据上述根节点所在位置划分区间，拿到左区间递归构建[left,maxIdx-1]
root.right：根据上述根节点所在位置划分区间，拿到右区间递归构建[maxIdx+1,right]

👻方法1：递归构建

/**
 * 654 最大二叉树
 */
public class Solution1 {

    public TreeNode constructMaximumBinaryTree(int[] nums) {
        TreeNode node = buildHelper(nums, 0, nums.length - 1); // 对照取闭区间
        return node;
    }

    // 根据指定区间构建树 root、left、right
    public TreeNode buildHelper(int[] nums, int left, int right) {

        // 基于前序思路构建树，此处验证区间有效性
        if (left > right) {
            return null;
        }

        // root 构建：获取当前指定区间的最大值max及其索引位置maxIdx
        int max = Integer.MIN_VALUE;
        int maxIdx = -1;
        for (int i = left; i <= right; i++) { // 此处如果取闭区间，注意区间传参
            if (nums[i] > max) {
                // 更新最大值和相应索引
                max = nums[i];
                maxIdx = i;
            }
        }

        // 根据root节点索引划分左右区间：L[left,maxIdx-1]、D(maxIdx)、R[maxIdx+1,right](结合题意：最大值左侧为左区间、最大值右侧为右区间)
        TreeNode root = new TreeNode(max);
        root.left = buildHelper(nums, left, maxIdx - 1);
        root.right = buildHelper(nums, maxIdx + 1, right);

        // 返回构建的节点
        return root;
    }

}

复杂度分析
- 时间复杂度：
- 空间复杂度：

另一种写法：将获取最大值单独抽离出来

/**
 * 🟡654 最大二叉树
 */
public class Solution654_01 {

    public TreeNode constructMaximumBinaryTree(int[] nums) {
        TreeNode root = buildHelper(nums, 0, nums.length - 1);
        return root;
    }

    /**
     * 递归构建二叉树
     * @param nums 数组列表
     * @param left 区间左界限
     * @param right 区间右界限
     * @return
     */
    public TreeNode buildHelper(int[] nums, int left, int right) {
        // 递归出口
        if (left > right) {
            return null;
        }

        // 构建节点
        int[] max = getMax(nums, left, right);
        int nodeIdx = max[0];
        int nodeVal = max[1];
        TreeNode node = new TreeNode(nodeVal);

        // 递归构建左、右节点
        node.left = buildHelper(nums, left, nodeIdx - 1);
        node.right = buildHelper(nums, nodeIdx + 1, right);

        // 返回构建的节点
        return node;
    }

    // 获取指定区间范围的nums的最大值
    public int[] getMax(int[] nums, int left, int right) {
        int maxVal = nums[left]; // Integer.MIN
        int maxIdx = left; // -1
        for (int i = left; i <= right; i++) {
            if (nums[i] > maxVal) {
                maxVal = nums[i];
                maxIdx = i;
            }
        }
        // 返回数组元素{maxIdx,maxVal}分表表示当前数组指定区间范围内的最大值和其对应索引
        return new int[]{maxIdx, maxVal};
    }

}

🍚二叉搜索树专题

🟢二叉搜索树的搜索（700）

1.题目内容open in new window

给定二叉搜索树（BST）的根节点 root 和一个整数值 val。

你需要在 BST 中找到节点值等于 val 的节点。返回以该节点为根的子树。如果节点不存在，则返回 null 。

2.题解思路

核心思路：最硬核的方式是延续遍历普通二叉树的思路（BFS、DFS）检索目标值是否存在，但此处还可进一步利用二叉搜索树的特性来优化算法实现。

当遍历节点值val大于target ，则说明目标值在树左侧，往左侧搜索即可
当遍历节点值val小于target ，则说明目标值在树右侧，往右侧搜索即可

👻方法1：迭代法

思路分析：遍历每个节点，然后根据当前遍历节点切换左右遍历方向，如果遍历到子节点都没找到target则说明无匹配

/**
 * 700 二叉搜索树中的搜索
 */
public class Solution1 {

    public TreeNode searchBST(TreeNode root, int val) {

        while (root != null) {
            // 根据二叉搜索树特性进行检索
            int cur = root.val;
            if (cur == val) {
                return root;
            } else {
                // 根据cur与val的关系切换遍历方向
                if (cur > val) {
                    root = root.left;
                } else {
                    root = root.right;
                }
            }
        }

        // 未找到
        return null;
    }

}

复杂度分析
- 时间复杂度：
- 空间复杂度：

/**
 * 🟢 700 二叉搜索树中的搜索 - https://leetcode.cn/problems/search-in-a-binary-search-tree/description/
 */
public class Solution700_03 {

    /**
     * 思路分析：基于迭代思路检索，定义遍历指针指向遍历节点，然后根据值比较缩小范围直到叶子节点
     */
    public TreeNode searchBST(TreeNode root, int val) {
        if (root == null) {
            return null;
        }

        // 定义遍历指针
        TreeNode cur = root; // 初始化指向根节点
        while (cur != null) {
            // 校验遍历节点值
            if (cur.val == val) {
                return cur;
            } else if (cur.val > val) {
                // 目标值在左子树，遍历指针向左移动
                cur = cur.left;
            } else if (cur.val < val) {
                // 目标值在右子树，遍历指针向右移动
                cur = cur.right;
            }
        }
        // 没有找到目标
        return null;
    }
}

👻方法2：递归法

递归思路：传统方式是基于深度优先遍历的思路，判断每个节点的值是否等于target，如果等于直接返回该节点。如果不等于target，则继续递归遍历其左、右子树，直到找到满足条件的内容
- 此处要使用到二叉搜索树的特性，核心在于递归分支的选择，每次只需要根据当前节点值和target的大小选择性递归，而不需要递归所有节点子树

// 递归法(基于DLR思路)
public TreeNode searchBST(TreeNode root, int val) {
    // 递归出口
    if (root == null) {
        return null;
    }

    // 递归逻辑
    if (root.val == val) {
        return root;
    }

    // 分别递归左右子树（递归遍历左、右子树（只要两者中存在即满足，要么在左边、要么在右边））
    TreeNode left = searchBST(root.left, val);
    TreeNode right = searchBST(root.right, val);
    return left != null ? left : right;
}


/**
 * 🟢700 二叉搜索树中的搜索
 */
public class Solution700_01 {

    public TreeNode searchBST(TreeNode root, int val) {
        TreeNode findNode = dfs(root, val);
        return findNode;
    }

    // dfs 递归搜索（递归法（利用二叉搜索树特性））
    public TreeNode dfs(TreeNode node, int target) {
        if (node == null) {
            return null;
        }

        if (node.val == target) {
            return node;
        }

        /**
    	 * 利用二叉搜索树的特性来判断要递归哪个子树
    	 * 当前节点值大于target，递归左子树
   	  	 * 当前节点值小于target，递归右子树
    	 */
        // 递归搜索左、右子树(利用二叉搜索树特性：左子树的节点小于右子树的节点)
        return (target < node.val) ? dfs(node.left, target) : dfs(node.right, target);
    }
}

复杂度分析
- 时间复杂度：
- 空间复杂度：

🟡验证二叉搜索树（098）

1.题目内容open in new window

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树

有效二叉搜索树定义如下：

节点的左子树只包含小于当前节点的数
节点的右子树只包含大于当前节点的数
所有左子树和右子树自身必须也是二叉搜索树

2.题解思路

👻方法1：中序遍历 + 验证升序

思路分析：利用二叉搜索树特性，二叉搜索树的中序遍历序列是升序的，如果不满足则非二叉搜索树。因此可以将题意转化为【中序遍历+升序验证】
- 如果采用迭代的思路只需要遍历的过程中进行验证即可，不需要将整个中序序列都先求得再遍历
- 数值类型：注意测试用例中一些临界值，此处可以调整为long处理，避免数值溢出导致错误

/**
 * 098 验证二叉搜索树
 */
public class Solution1 {

    public boolean isValidBST(TreeNode root) {
        if(root==null){
            return true;
        }
        List<Integer> list = new ArrayList<>();
        dfs(root,list);
        // 验证中序序列是否升序
        for(int i=0;i<list.size()-1;i++){
            if(list.get(i)>=list.get(i+1)){ // 出现相等或者降序的情况
                return false;
            }
        }
        // 验证通过
        return true;
    }


    // 中序遍历验证升序
    public void dfs(TreeNode node, List<Integer> list){
        if(node==null){
            return;
        }

        // LDR 中序遍历
        dfs(node.left,list);
        list.add(node.val);
        dfs(node.right,list);
    }

}

复杂度分析
- 时间复杂度：
- 空间复杂度：

中序遍历 + 验证升序（用pre记录上一个遍历节点）

/**
 * 098 验证二叉搜索树
 */
public class Solution4 {

    // int preVal = Integer.MIN_VALUE;// 定义当前遍历节点的上一个节点的值（此处只需要校验值，因此定义为数值类型，也可定义为TreeNode，但需注意NPE处理）
    long preVal = Long.MIN_VALUE; // 注意数值取值范围

    public boolean isValidBST(TreeNode root) {
        return dfs(root);
    }

    // 中序遍历验证：中序遍历+相邻两数比较，此处引入pre优化空间复杂度，不需要定义列表存储所有的中序序列元素
    public boolean dfs(TreeNode node) {
        if (node == null) {
            return true;
        }
        // 左(校验左子树)
        if(!dfs(node.left)){
            return false;
        }

        // 中
        // 比较元素（判断cur和pre是否满足二叉搜索树条件）
        if(node.val<=preVal){
            return false; // 当前遍历节点值小于等于上一个节点值，非升序，返回false
        }
        // 更新pre节点值（当前节点值会作为下一个遍历节点的preVal）
        preVal = node.val;

        // 右(校验右子树)
        return dfs(node.right);
    }

}


/**
 * 🟡 098 验证二叉搜索树
 */
public class Solution098_03 {

    // public int preVal = Integer.MIN_VALUE; // 定义字段维护当前遍历节点的上一个中序序列的值
    public long preVal = Long.MIN_VALUE;

    // LDR:中序遍历，校验中序遍历序列是否为连续升序(空间优化版本)
    public boolean isValidBST(TreeNode root) {
        List<Integer> list = new ArrayList<>();
        return inorder(root);
    }

    // 中序遍历
    public boolean inorder(TreeNode node) {
        if (node == null) {
            return true;
        }
        // 校验左子树
        boolean left  = inorder(node.left);

        // 处理节点（校验中序序列有序性）
        if (preVal >= node.val) {
            return false; // 非升序序列
        } else {
            preVal = node.val; // 更新
        }

        // 校验右子树
        boolean right = inorder(node.right);

        return left && right;
    }
}

👻方法2：DFS（前序遍历思路）

思路分析：根据定义确定递归规则
- 遍历每个节点，不仅当前节点要满足left < cur < right，且其左右子树也要满足这个条件（注意数值溢出问题，调整为Long类型处理）
- 从根节点开始搜索，每个节点都当做根节点，根节点值不能小于最小值，不能大于最大值，每次根据搜索方向改变当前最大最小值即可
  - 当搜索左子树时，最大值就是根节点值 = 》【left，cur】
  - 当搜索右子树时，最小值就是根节点值 =》【cur，right】
- 数值类型：注意测试用例中一些临界值，此处可以调整为long处理，避免数值溢出导致错误

/**
 * 098 验证二叉搜索树
 */
public class Solution3 {

    // DFS 前序遍历思路
    public boolean isValidBST(TreeNode root) {
        return dfs(root, Integer.MIN_VALUE, Integer.MAX_VALUE);
    }

    // 前序遍历思路
    public boolean dfs(TreeNode node, int minVal, int maxVal) {
        if (node == null) {
            return true;
        }
        // 当前节点值
        int cur = node.val;
        // 需满足二叉搜索树属性left<cur<right，且其子树也要满足这个特性
        return cur > minVal && cur < maxVal && dfs(node.left, minVal, cur) && dfs(node.right, cur, maxVal);
    }

}

复杂度分析
- 时间复杂度：
- 空间复杂度：

❌ 错误思路分析

根据二叉搜索树的定义，左子树节点均小于当前节点、右子树节点均大于当前节点，且左、右子树也均满足二叉搜索树定义。则基于递归的思路可能会联想到采用DFS遍历节点进行校验，进而得到下述代码

/**
 * 🟡 098.验证二叉搜索树 - https://leetcode.cn/problems/validate-binary-search-tree/description/
 */
public class Solution098_01 {

    /**
     * 校验节点是否为一个有效的二叉搜索树
     */
    public boolean isValidBST(TreeNode root) {
        return valid(root);
    }

    // 递归思路
    private boolean valid(TreeNode node) {
        if (node == null) {
            return true;
        }

        // 校验节点
        if (node.left != null) {
            if (node.left.val >= node.val) {
                return false;
            }
        }
        if (node.right != null) {
            if (node.right.val <= node.val) {
                return false;
            }
        }

        // 递归校验左、右子树是否满足二叉搜索特性
        boolean validLeft = valid(node.left);
        boolean validRight = valid(node.right);
        return validLeft && validRight;
    }
}

虽然看上去逻辑好像挺顺畅的，但是实际上此处会忽略下面这种树，在递归的过程中并没有保证到节点右侧的节点均大于当前节点值，进而导致验证错误。实际上此处验证核心的切入还要从二叉搜索树的特性入手：二叉搜索树的中序遍历序列呈现递增趋势，基于此可以在遍历的过程中采用DFS（LDR）的顺序进行遍历，然后校验是否满足递增规律（在这个过程中记录preNodeVal上一个遍历节点值）

🟢二叉搜索树的最小绝对值差（530）

1.题目内容open in new window

给你一个二叉搜索树的根节点 root ，返回 树中任意两不同节点值之间的最小差值 。

差值是一个正数，其数值等于两值之差的绝对值。

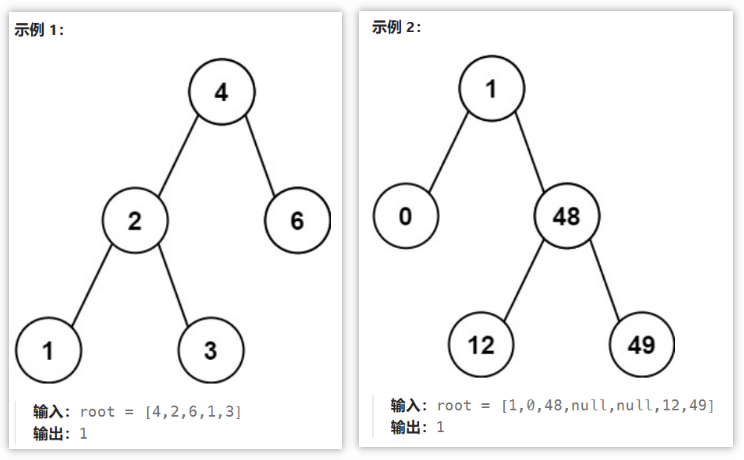
2.题解思路

👻方法1：中序遍历+相邻两数比较

思路分析：对中序遍历后的序列进行最小值绝对值判断（相邻两数比较）
- 考虑对升序数组 a 求任意两个元素之差的最小值，答案一定为相邻两个元素之差的最小值。因此结合二叉搜索树的特性（中序遍历序列是升序的）则可将题意转化为【中序遍历+相邻两数比较】

/**
 * 530 二叉搜索树的最小绝对差
 */
public class Solution1 {

    public int getMinimumDifference(TreeNode root) {
        if(root==null){
            return 0;
        }

        // 1.获取中序序列
        List<Integer> list = new ArrayList<>();
        ldr(root,list);
        // 2.校验相邻两数
        int minSubVal = Integer.MAX_VALUE;
        for(int i=0;i<list.size()-1;i++){
            // 更新最小绝对差
            // minSubVal = Math.min(minSubVal,Math.abs(list.get(i+1)-list.get(i)));
             minSubVal = Math.min(minSubVal,list.get(i+1)-list.get(i)); // 元素本身有序 不需要abs
        }
        // 返回结果
        return minSubVal;
    }

    // 中序遍历（LDR）
    public void ldr(TreeNode node, List<Integer> list){
        if(node==null){
            return;
        }
        ldr(node.left,list);
        list.add(node.val);
        ldr(node.right,list);
    }
}

复杂度分析
- 时间复杂度：O（n）需遍历所有的树节点
- 空间复杂度：O（n）需借助List存储中序遍历序列，然后基于这个序列计算相邻两数的值的最小情况（最小绝对差处理）

👻方法2：引入pre优化空间效率

递归（引入pre概念优化空间复杂度，pre用于记录当前遍历节点的上一个节点的相关信息）

/**
 * 530 二叉搜索树的最小绝对差
 */
public class Solution2 {

    TreeNode preNode = null; // 记录当前遍历节点的上一个节点

    int minSubVal = Integer.MAX_VALUE;

    public int getMinimumDifference(TreeNode root) {
        if (root == null) {
            return 0;
        }
        // 中序遍历
        ldr(root);
        // 返回结果
        return minSubVal;
    }

    // 中序遍历（LDR）
    public void ldr(TreeNode node) {
        if (node == null) {
            return;
        }
        // 左
        ldr(node.left);

        // 中
        // 更新minSubVal（注意NPE处理：也是对初始状态perNode的处理）
        if (preNode != null) {
            minSubVal = Math.min(minSubVal, node.val - preNode.val);
        }

        // 更新preNode指针
        preNode = node; // 当前遍历节点会作为下一个节点的pre（其更新时机是跟着"中"这个步骤后面走）

        // 右
        ldr(node.right);
    }
}

复杂度分析

时间复杂度：O（n）需遍历所有的树节点
空间复杂度：O（1）引入pre概念，优化了空间复杂度，在遍历的过程中进行比较、滚动更新min和pre，不用记录整个中序序列

/**
 * 🟢530 二叉搜索树的最小绝对差
 */
public class Solution530_01 {

    public long preVal = Long.MAX_VALUE; // 记录当前遍历节点的上一个节点值（基于中序遍历）
    public long minSubVal = Long.MAX_VALUE; // 记录最小绝对差值

    public int getMinimumDifference(TreeNode root) {

        // 调用递归算法处理
        dfs(root);

        return (int) minSubVal;
    }

    // 基于中序遍历进行校验，获取最小绝对差
    public void dfs(TreeNode node) {
        if (node == null) {
            return;
        }

        // 递归处理左节点
        dfs(node.left);

        // 处理节点
        if (preVal != Integer.MAX_VALUE) {
            minSubVal = Math.min(minSubVal, Math.abs(node.val - preVal));
        }
        preVal = node.val;

        // 递归处理右节点
        dfs(node.right);
    }

    public static void main(String[] args) {
        TreeNode node1 = new TreeNode(1);
        TreeNode node2 = new TreeNode(0);
        TreeNode node3 = new TreeNode(48);
        TreeNode node4 = new TreeNode(12);
        TreeNode node5 = new TreeNode(49);
        node1.left = node2;
        node1.right = node3;
        node3.left = node4;
        node3.right = node5;

        Solution530_01 s = new Solution530_01();
        s.getMinimumDifference(node1);
    }

}

🟢二叉搜索树中的众数（501）

1.题目内容open in new window

给你一个含重复值的二叉搜索树（BST）的根节点 root ，找出并返回 BST 中的所有众数open in new window（即，出现频率最高的元素）。

如果树中有不止一个众数，可以按 任意顺序 返回。

假定 BST 满足如下定义：

结点左子树中所含节点的值 小于等于 当前节点的值
结点右子树中所含节点的值 大于等于 当前节点的值
左子树和右子树都是二叉搜索树

2.题解思路

核心思路：

【1】普通方式：遍历+频率统计
【2】基于方法【1】中的思路优化空间复杂度

👻方法1：硬核遍历+频率统计

/**
 * 501 二叉搜索树中的众数
 */
public class Solution1 {

    public int[] findMode(TreeNode root) {
        if (root == null) {
            return new int[]{};
        }

        // 获取中序遍历序列，统计众数
        List<Integer> list = new ArrayList<>();
        dfs(root, list);

        Map<Integer, Integer> map = new HashMap<>();
        int maxCount = 0; // 更新最大频次信息
        for (int item : list) {
            int cur = map.getOrDefault(item, 0);
            map.put(item, cur + 1);
            maxCount = Math.max(maxCount, cur + 1); // 更新最新的频次和最大频次关系
        }

        List<Integer> res = new ArrayList<>();
        // 遍历频次信息，构建众数结果集
        Set<Integer> ketSet = map.keySet();
        Iterator<Integer> iterator = ketSet.iterator();
        while (iterator.hasNext()) {
            int curKey = iterator.next();
            if (map.get(curKey) == maxCount) {
                res.add(curKey);
            }
        }

        int[] resArr = new int[res.size()];
        for (int i = 0; i < res.size(); i++) {
            resArr[i] = res.get(i);
        }

        // 返回结果集
        return resArr;
    }

    // 中序遍历
    public void dfs(TreeNode node, List<Integer> list) {
        if (node == null) {
            return;
        }
        dfs(node.left, list);
        list.add(node.val);
        dfs(node.right, list);
    }

}

复杂度分析
- 时间复杂度：O（n），需遍历所有树节点、统计节点出现频次、再次遍历获取到最大出现频次的数据并封装结果，这个过程中涉及到3次遍历处理操作
- 空间复杂度：O（n），在遍历处理的过程中需构建辅助集合处理

/**
 * 🟢 二叉搜索树中的众数 - https://leetcode.cn/problems/find-mode-in-binary-search-tree/description/
 */
public class Solution501_01 {

    private List<Integer> list = new ArrayList<>();

    /**
     * 寻找二叉搜索树中出现次数最多的数字（一个或多个，树节点值可重复）
     */
    public int[] findMode(TreeNode root) {
        // 调用递归检索
        inorder(root);
        // 获取list中的众数
        Map<Integer,Integer> map = new HashMap<>();
        for(int num : list){
            map.put(num,map.getOrDefault(num,0)+1);
        }

        List<Integer> res = new ArrayList<>();
        // 校验众数
        int maxCnt = -1;
        int maxVal = Integer.MIN_VALUE;
        Set<Integer> keySet = map.keySet();
        for(int key : keySet){
            int curCnt = map.get(key);
            if(curCnt>maxCnt){
                // 出现了频次更高的选项
                maxCnt = curCnt;
                maxVal = key;
                // 清空当前结果集，加入更高出现频次的数字
                list.clear();
                list.add(key);
            }else if(curCnt==maxCnt){
                // 出现了相同频次的选项,直接加入
                list.add(key);
            }else{
                // 无操作
            }
        }

        // 返回结果
        return list.stream().mapToInt(Integer::valueOf).toArray();
    }

    // 递归搜索
    private void inorder(TreeNode node){
        if(node==null){
            return;
        }

        // 中序遍历（LDR）
        inorder(node.left);
        list.add(node.val);
        inorder(node.right);
    }

}

针对【方法2中空间复杂度的优化】，本质上也是基于滚动变量的思路去调整上述算法，核心关注curKey、curCnt、maxCnt、res(结果集)，先更新当前遍历节点和出现频次，随后基于此更新最大出现频次（避免概念混淆）

👻方法2：中序遍历（优化空间复杂度）

思路分析
- 基于中序遍历的思路，此处要优化的方向是【思路1】中的中序遍历序列存储和元素出现频率统计的空间复杂度和实现复杂度，希望可以在中序遍历的过程中就能够同步得到这个众数结果集，可以从以下节点切入，通过定义当前遍历节点、节点出现频次、最大出现频次、众数结果集合在遍历的过程中维护这些参数来优化复杂度
- 本质上切入的核心就是在LDR中序遍历的使用去更新这些定义的参数来达到同步维护的目的，而这个更新的过程可以单独抽离成一个方法，然后实现如下逻辑
  - （1）更新节点及其出现频次（将curNodeVal与当前遍历节点值val进行比较）
    - curNodeVal!=val：说明出现了新元素，需要进行重置（当前遍历节点、次数重置为1）
    - curNodeVal==val：连续出现的重复元素，计数累加即可
  - （2）更新maxCount当前的最大出现次数（将curNodeCount与maxCount进行比较）
    - curNodeCount==maxCount：说明出现了同样的众数，将当前的curNodeVal加入结果集
    - curNodeCount>maxCount：说明有频次更多的众数出现，需要取消目前的结果集（res置空）并更新目前的最新的maxCount、res
    - curNodeCount<maxCount：无任何操作
  - ==注意点：==此处注意为了避免思路混淆和重复处理，拆分为上述两个步骤，在更新完节点及其出现频次之后再更新max概念，思路会更加清晰

/**
 * 501 二叉搜索树中的众数
 */
public class Solution2 {

    // 定义当前遍历节点、出现频次、最大出现频次、众数结果集合
    List<Integer> res = new ArrayList<>();
    int curNodeVal;
    int curNodeCount = 0;
    int maxCount = 0;

    public int[] findMode(TreeNode root) {
        // 调用中序遍历方法
        dfs(root);
        // 封装结果集
        int[] nums = new int[res.size()];
        for (int i = 0; i < res.size(); i++) {
            nums[i] = res.get(i);
        }
        return nums;
    }

    // 中序遍历:此处借助辅助参数构建以优化空间复杂度，不需要存储整个中序序列
    public void dfs(TreeNode node) {
        if (node == null) {
            return;
        }

        // 左
        dfs(node.left);

        // 中(遍历当前节点，调用更新方法)
        update(node.val);

        // 右
        dfs(node.right);
    }

    public void update(int targetVal) {
        // 1.更新当前节点和相应计数
        if (curNodeVal != targetVal) { // 说明是新元素出现（如果是重复元素的话会存在连续相等的情况）
            // 新元素加入，重置计数
            curNodeVal = targetVal;
            curNodeCount = 1; // 节点计数重置计数
        } else {
            // 出现连续重复元素，统计累计，更新curNodeCount
            curNodeCount++;
        }

        // 2.maxCount更新
        if (curNodeCount == maxCount) {
            // 说明出现重复众数，加入结果集
            res.add(curNodeVal);
        } else if (curNodeCount > maxCount) {
            // 当前元素出现次数大于maxCount，说明出现了新的众数，直接清空当前的结果集并更新maxCount，开始新一轮校验
            maxCount = curNodeCount;
            res.clear();
            res.add(curNodeVal);
        }
    }

}

复杂度分析
- 时间复杂度：
- 空间复杂度：

🟡二叉搜索树中的插入操作（701）

1.题目内容open in new window

给定二叉搜索树（BST）的根节点 root 和要插入树中的值 value ，将值插入二叉搜索树。返回插入后二叉搜索树的根节点。输入数据保证，新值和原始二叉搜索树中的任意节点值都不同。

注意，可能存在多种有效的插入方式，只要树在插入后仍保持为二叉搜索树即可。你可以返回 任意有效的结果

2.题解思路

👻方法1：迭代法

思路分析：定义指针遍历树节点，根据二叉搜索树特性确定遍历方向
- 由于此处并没有限定插入val后的树必须为平衡二叉树，因此可以遍历每个节点，根据val大小与当前遍历节点的值进行对比，将其插入左侧/右侧
  - 如果要插入的val小于当前遍历节点值cur.val，则判断其左节点是否为空，为空则可插入（插入完成需跳出循环，或者直接return插入后的结果），不为空则继续往左遍历
  - 如果要插入的val大于当前遍历节点值cur.val，则判断其右节点是否为空，为空则可插入（插入完成需跳出循环，或者直接return插入后的结果），不为空则继续往右遍历

/**
 * 701 二叉树中的插入操作
 */
public class Solution1 {

    public TreeNode insertIntoBST(TreeNode root, int val) {
        if (root == null) {
            return new TreeNode(val);
        }

        // 定义遍历节点
        TreeNode cur = root;
        while (cur != null) {
            // 根据当前遍历节点值判断
            if (val < cur.val) {
                // 判断当前其左节点是否为空，为空则可插入
                if (cur.left == null) {
                    cur.left = new TreeNode(val);
                    break; // 节点插入完成，跳出循环
                } else {
                    cur = cur.left; // 继续寻找下一个可插入位置
                }
            } else if (val > cur.val) {
                // 判断当前其右节点是否为空，为空则可插入
                if (cur.right == null) {
                    cur.right = new TreeNode(val);
                    break; // 节点插入完成，跳出循环
                }else {
                    cur = cur.right; // 继续寻找下一个可插入位置
                }
            }
        }
        // 返回结果
        return root;
    }

}

复杂度分析
- 时间复杂度：O（n）n 为树节点个数
- 空间复杂度：O（1）

👻方法2：递归思路

思路分析：递归创建节点，判断的思路和迭代的思路类似
- 递归出口：
- 递归过程：根据当前节点值和插入节点值进行判断
  - 如果node为null，构建新节点
  - 如果node不为null
    - 如果node.val > val，需要将节点插入到当前节点左侧
    - 如果node.val < val，需要将节点插入到当前节点右侧

/**
 * 701 二叉树中的插入操作
 */
public class Solution2 {

    public TreeNode insertIntoBST(TreeNode root, int val) {
        if (root == null) {
            return new TreeNode(val);
        }
        // 递归构建
        return buildHelper(root, val);
    }

    // 递归创建
    public TreeNode buildHelper(TreeNode node, int val) {
        if (node == null) {
            return new TreeNode(val);
        }

        // 根据当前节点值和插入节点值进行判断
        if (node.val > val) {
            // 插入到左侧
            node.left = buildHelper(node.left, val);
        }

        if (node.val < val) {
            // 插入到右侧
            node.right = buildHelper(node.right, val);
        }
        return node;
    }

}

复杂度分析
- 时间复杂度：O（n）n 为树节点个数
- 空间复杂度：取决于递归栈的深度

👻方法3：模拟法

思路分析：中规中矩按照模拟的思路处理二叉搜索树的插入操作，经历一个【树->列表（插入新节点）->树】的过程
- ① 构建二叉搜索树中序遍历序列list
- ② 将指定val插入中序遍历序列（二分法或者直接遍历）
- ③ 将更新后的list重新构建为平衡树（参考[108-将有序数组转化为平衡二叉搜索树]思路）

/**
 * 🟡701 二叉搜索树中的插入操作
 */
public class Solution701_01 {

    public TreeNode insertIntoBST(TreeNode root, int val) {
        // ① 获取二叉搜索树的中序遍历序列
        List<Integer> list = new ArrayList<>();
        dfs(root, list);

        // ② 将val插入中序遍历序列中适合的位置
        insertByBinarySearch(list, val);

        // ③ 递归构建二叉搜索树
        return buildHelper(list, 0, list.size() - 1);
    }

    // ① dfs(ldr:中序遍历)
    public void dfs(TreeNode node, List<Integer> list) {
        if (node == null) {
            return;
        }

        dfs(node.left, list);
        list.add(node.val);
        dfs(node.right, list);

    }

    // ② 二分法搜索，并插入序列在合适位置
    public void insertByBinarySearch(List<Integer> list, int val) {
        int left = 0, right = list.size() - 1;
        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (list.get(mid) == val) {
                return;
            } else if (list.get(mid) < val) {
                left = mid + 1;
            } else if (list.get(mid) > val) {
                right = mid - 1;
            }
        }
        // 将val元素插入到left指定位置
        list.add(left, val);
    }

    // ③ 根据中序遍历序列构建二叉搜索树
    public TreeNode buildHelper(List<Integer> list, int left, int right) {
        if (left > right) {
            return null;
        }
        // 构建节点
        int mid = (left + right) / 2;
        TreeNode node = new TreeNode(list.get(mid));
        node.left = buildHelper(list, left, mid - 1);
        node.right = buildHelper(list, mid + 1, right);
        // 返回构建节点
        return node;
    }

    public static void main(String[] args) {
        TreeNode node1 = new TreeNode(4);
        TreeNode node2 = new TreeNode(2);
        TreeNode node3 = new TreeNode(7);
        TreeNode node4 = new TreeNode(1);
        TreeNode node5 = new TreeNode(3);
        node1.left = node2;
        node1.right = node3;
        node2.left = node4;
        node2.right = node5;
        Solution701_01 s = new Solution701_01();
        s.insertIntoBST(node1, 5);
    }
}

🟡删除二叉搜索树中的节点（450）

1.题目内容

给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

一般来说，删除节点可分为两个步骤：

首先找到需要删除的节点；
如果找到了，删除它；

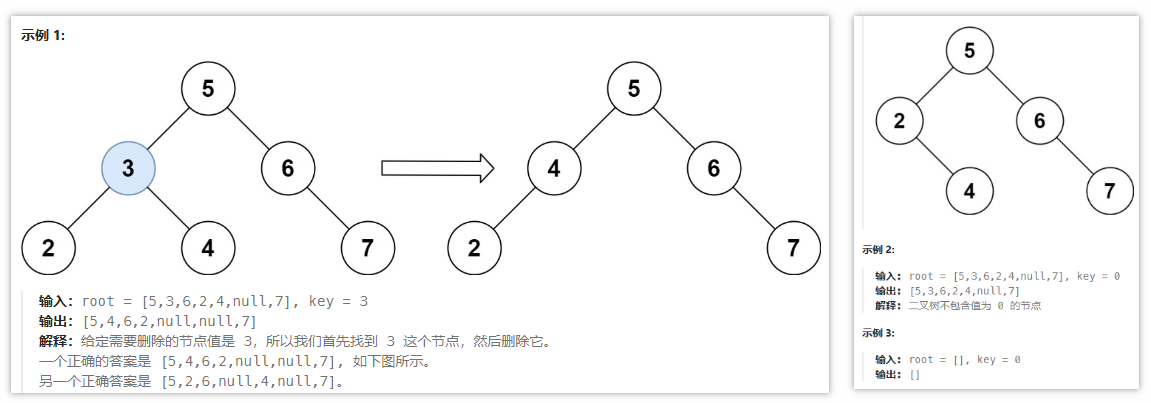
2.题解思路

👻方法1：迭代法（查找target+处理节点关系）

思路分析：迭代的方式最暴力的就是找到目标节点（并记录其上一个遍历节点pre），然后处理节点关系
- （1）迭代：找到目标节点（根据二叉搜索树的迭代检索，找到目标val就跳出循环）
  - 定义cur节点指针用于遍历，用pre记录上一个遍历节点（后续更新会用到），如果找到目标val就跳出循环（此处跳出循环条件有两个：找到val或者val不存在）
    - cur为null 表示 val 不存在，则直接返回root
    - cur不为null 表示循环在遍历过程中退出了，cur指向当前待删除节点，继续执行下述步骤（2）
- （2）处理节点关系（获取newChildNode，根据pre更新挂载关系）
  - 更新待删除节点左右节点关系，构建新的子树（新的子树根节点newChildNode）
    - 左右子节点为空：可以直接删除cur节点，构建后的newChildNode节点为null
    - 左节点为空、右节点不为空：删除cur节点后，右节点上位，newChildNode=curRight
    - 左节点不为空、右节点为空：删除cur节点后，左节点上位，newChildNode=curLeft
    - 左右节点都不为空：删除cur节点后，需要将原curLeft挂载在curRight的最左节点的左子树，newChildNode为更新后的curRight
  - 根据pre节点判断newChildNode的挂载位置
    - pre 为 null，删除的是根节点，因此 newChildNode 就是删除后的新树
    - pre 不为 null，判断原来删除的节点位置是在左还是右（看其左右节点的值和val等值比较或者比较当前节点与val大小比较）
      - pre.left.val == val 左边，则将newChildNode 挂在 pre 左侧，返回挂载更新后的根节点root
      - pre.right.val == val 右边，则将newChildNode 挂在 pre 右侧，返回挂载更新后的根节点root

/**
 * 450 删除二叉搜索树中的节点
 */
public class Solution2 {

    // 迭代法：遍历树节点，找到要删除的目标节点，如果目标节点存在左右节点则需进行处理 todo 覆盖场景不足
    public TreeNode deleteNode(TreeNode root, int key) {
        if (root == null) {
            return null;
        }

        // 遍历树节点，找到目标节点
        TreeNode cur = root;
        TreeNode pre = null; // 记录每个节点的上一个遍历节点
        while (cur != null) {
            if (key == cur.val) {
                break; // 找到目标节点，跳出循环，等待处理
            } else if (key < cur.val) {
                pre = cur; // 更新pre
                cur = cur.left; // 去左边找
            } else if (key > cur.val) {
                pre = cur; // 更新pre
                cur = cur.right; // 去右边找
            }
        }

        // 判断cur的值是否存在（不存在则说明待删除的目标节点，存在则说明需要处理这个待删除的目标节点）
        if (cur == null) {
            return root; // 没找到待删除的目标节点，直接返回root
        }

        /**
         * 删除目标节点操作包括两部分：
         * 1.处理待删除目标节点的左右子节点关系（判断左右子节点是否为null，根据情况分析），得到删除该节点之后重新构建的子树根节点newChildNode（它会被拼在原pre上）
         *   - 左右子节点为空：可以直接删除cur节点，构建后的newChildNode节点为null
         *   - 左节点为空、右节点不为空：删除cur节点后，右节点上位，newChildNode为curRight
         *   - 左节点不为空、右节点为空：删除cur节点后，左节点上位，newChildNode为curLeft
         *   - 左右节点都不为空：删除cur节点后，需要将原curLeft挂载在curRight的最左节点的左子树，newChildNode为更新后的curRight
         * 2.根据步骤1中得到的新子树，结合pre节点判断该子树挂载位置
         *   - pre 为 null，删除的是根节点，因此 newChildNode 就是删除后的新树
         *   - pre 不为 null，判断原来删除的节点位置是在左还是右（看其左右节点的值和val比较）
         *        - pre.left == val 左边，则将newChildNode 挂在 pre 左侧
         *        - pre.right == val 右边，则将newChildNode 挂在 pre 右侧
         */
        // 1.处理待删除目标节点的左右子节点关系
        TreeNode newChildNode;
        TreeNode curLeft = cur.left;
        TreeNode curRight = cur.right; // 新子树节点，原删除节点的左、右节点
        if (curLeft == null && curRight == null) {
            newChildNode = null;
        } else if (curLeft != null && curRight == null) {
            newChildNode = curLeft;
        } else if (curLeft == null && curRight != null) {
            newChildNode = curRight;
        } else {
            // 找到右子树的最左节点
            TreeNode findLeft = curRight;
            while (findLeft.left != null) {
                findLeft = findLeft.left;
            }
            // 将原左子树挂载到右子树的最左节点的左侧
            findLeft.left = curLeft;
            // 更新后的右子树作为新的子树根节点
            newChildNode = curRight;
        }

        // 2.根据pre的值判断将newChildNode挂载到哪个位置
        if (pre == null) {
            return newChildNode; // 删除的是根节点，则新构建的子树根节点就是所得
        }

        // pre 不为null，将pre的左右节点值与val比较，看其原来是在左边还是右边
        if (pre.left != null && pre.left.val == key) {
            pre.left = newChildNode;

        } else if (pre.right != null && pre.right.val == key) {
            pre.right = newChildNode;
        }
        // 返回处理后的结果
        return root;
    }
}

复杂度分析
- 时间复杂度：O（n）n 为树节点个数
- 空间复杂度：O（1）

迭代法（参考代码规范和思路设计），将方法抽离整合

class Solution {
  public TreeNode deleteNode(TreeNode root, int key) {
    if (root == null){
      return null;
    }
    //寻找对应的对应的前面的节点，以及他的前一个节点
    TreeNode cur = root;
    TreeNode pre = null;
    while (cur != null){
      if (cur.val < key){
        pre = cur;
        cur = cur.right;
      } else if (cur.val > key) {
        pre = cur;
        cur = cur.left;
      }else {
        break;
      }
    }
    if (pre == null){
      return deleteOneNode(cur);
    }
    if (pre.left !=null && pre.left.val == key){
      pre.left = deleteOneNode(cur);
    }
    if (pre.right !=null && pre.right.val == key){
      pre.right = deleteOneNode(cur);
    }
    return root;
  }

  public TreeNode deleteOneNode(TreeNode node){
    if (node == null){
      return null;
    }
    if (node.right == null){
      return node.left;
    }
    TreeNode cur = node.right;
    while (cur.left !=null){
      cur = cur.left;
    }
    cur.left = node.left;
    return node.right;
  }
}

/**
 * 🟡 450 删除二叉搜索树中的节点
 */
public class Solution450_01 {

    /**
     * 核心思路：查找目标节点target（记录pre(父节点)） + 处理节点关系（构建删除后的新子树）
     * 删除二叉搜索树的节点，需注意对其子节点的处理（找到待删除节点，并处理子节点）
     * 1.左子节点left不为空，则left取代待删除节点的位置并将原来的右子节点放在最右
     * 2.右子节点right不为空，则right取代待删除节点的位置并将的原来的左子节点放在最左
     */
    public TreeNode deleteNode(TreeNode root, int key) {

        // ① 寻找目标target并记录其父节点
        TreeNode pre = null;
        TreeNode cur = root;
        while (cur != null) {
            // 校验cur.val与key的关系
            int curVal = cur.val;
            if (curVal == key) {
                break; // 跳出循环
            } else if (key < curVal) {
                pre = cur; // 记录pre
                cur = cur.left;
            } else if (key > curVal) {
                pre = cur; // 记录pre
                cur = cur.right;
            }
        }
        if (cur == null) {
            return root; // 目标节点不存在，直接返回
        }

        // ② 处理节点关系（校验目标节点的左右子树，构建新节点）
        TreeNode newChildNode;
        TreeNode curLeftNode = cur.left;
        TreeNode curRightNode = cur.right;
        if (curLeftNode == null && curRightNode == null) {
            // 左右子节点都为空，则删除该节点之后构建的新子节点为空
            newChildNode = null;
        } else if (curLeftNode == null && curRightNode != null) {
            // 左子节点为空，右子节点不为空，则右子节点上位
            newChildNode = curRightNode;
        } else if (curLeftNode != null && curRightNode == null) {
            // 左子节点不为空，右子节点为空，则左子节点上位
            newChildNode = curLeftNode;
        } else {
            // 左右子节点都不为空，可以将左子节点挂靠在右子节点的最左侧
            TreeNode findLeft = curRightNode;
            while (findLeft.left != null) {
                findLeft = findLeft.left;
            }
            findLeft.left = curLeftNode; // 将原左子节点挂靠在原右子节点的最左侧
            newChildNode = curRightNode; // 返回构建的新子节点
        }

        // ③ 拼接节点关系
        if (pre == null) {
            // 说明是初始化状态，那么只有待删除节点为root时才会出现，这种情况下直接返回构建的新节点
            return newChildNode;
        } else {
            // 校验pre.val与key的值，看目标值原来是在左侧还是右侧
            int preVal = pre.val;
            if (key < preVal) {
                pre.left = newChildNode;
            } else if (key > preVal) {
                pre.right = newChildNode;
            }
        }

        // 返回处理后的节点
        return root;
    }

}

👻方法2：递归法（DFS：DLR）

思路分析
- DFS（DLR）：
- root 为空，代表未搜索到值为 key 的节点，返回空
- root.val>key，表示值为 key 的节点可能存在于 root 的左子树中，需要递归地在 root.left 调用 deleteNode，并返回 root
- root.val<key，表示值为 key 的节点可能存在于 root 的右子树中，需要递归地在 root.right 调用 deleteNode，并返回 root
- root.val=key（求更新后的子树根节点），root 即为要删除的节点。此时要做的是删除 root，并将它的子树合并成一棵子树，保持有序性，并返回根节点。根据 root 的子树情况分成以下情况讨论：
  - root 为叶子节点，没有子树。此时可以直接将它删除，即返回空
  - root 只有左子树，没有右子树。此时可以将它的左子树作为新的子树，返回它的左子节点
  - root 只有右子树，没有左子树。此时可以将它的右子树作为新的子树，返回它的右子节点
  - root 有左右子树，这时可以将 root 的后继节点（比 root 大的最小节点，即它的右子树中的最小节点，记为 successor）作为新的根节点替代 root，并将 successor 从 root 的右子树中删除，使得在保持有序性的情况下合并左右子树

/**
 * 450 删除二叉搜索树的节点
 */
public class Solution4 {

    // 递归思路：DFS（DLR）
    public TreeNode deleteNode(TreeNode root, int key) {
        return dfsDelNode(root,key);
    }

    /**
     * 递归删除的核心：此处遍历顺序不影响操作的结果，可以选择DLR进行遍历
     * D：找到目标节点`node`
     * - 遍历节点值和key匹配，则根据该节点是否存在左右节点进行处理
     * - 更新删除该节点后的节点关系（返回更新后的子树，即删除该节点之后的更新的子树）
     * LR：递归执行操作，递归更新当前的左、右子树
     * 此处的思路与迭代的逻辑很类似
     */
    public TreeNode dfsDelNode(TreeNode node, int key) {
        // 如果指定节点为null，说明待删除节点不存在（或者本身root为null、或者遍历到了叶子节点位置）
        if (node == null) {
            return node;
        }

        // 如果指定节点不为null，则进一步校验值

        // D: 删除指定节点，更新节点关系
        if (key == node.val) {
            // 判断待删除节点的左右子树状态，分情况讨论
            TreeNode curLeft = node.left;
            TreeNode curRight = node.right;
            TreeNode refreshNode; // 定义删除当前节点后，根据左右子树状态更新后的新节点（可以挂载到pre上）
            // 分情况讨论
            if (curLeft == null && curRight == null) {
                // 左右节点均为空，可以直接删除该节点
                refreshNode = null;
            } else if (curLeft != null && curRight == null) {
                // 左节点不为空，右节点为空，则左节点上位成为新的子树节点
                refreshNode = curLeft;
            } else if (curLeft == null && curRight != null) {
                // 右节点不为空，左节点为空，则右节点上位成为新的子树节点
                refreshNode = curRight;
            } else {
                // 左右节点都不为空，则需将原左子节点挂载到原右子节点的最左节点，此时更新后的右节点上位成为新的子树节点
                TreeNode findLeft = curRight; // 定义遍历节点查找原右子节点的最左节点
                while (findLeft.left != null) {
                    findLeft = findLeft.left;
                }
                findLeft.left = curLeft; // 将原左子节点挂载到原右子节点的最左节点
                refreshNode = curRight; // 更新后的右节点上位成为新的子树节点
            }
            // 返回节点
            return refreshNode;
        }

        // L R
        if (key < node.val) {
            node.left = dfsDelNode(node.left, key); // 递归遍历左节点执行删除操作
        } else if (key > node.val) {
            // 递归操作
            node.right = dfsDelNode(node.right, key); // 递归遍历右节点执行删除操作
        }

        // 返回更新后的节点
        return node;
    }
}

复杂度分析
- 时间复杂度：
- 空间复杂度：

🟡修剪二叉搜索树（669）

1.题目内容open in new window

给你二叉搜索树的根节点 root ，同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树，使得所有节点的值在[low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 (即，如果没有被移除，原有的父代子代关系都应当保留)。可以证明，存在 唯一的答案

所以结果应当返回修剪好的二叉搜索树的新的根节点。注意，根节点可能会根据给定的边界发生改变

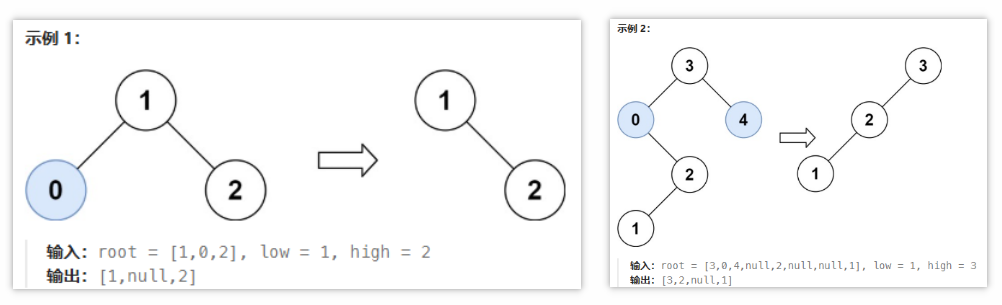
2.题解思路

思路误区：此处可能会基于模拟的思路，尝试遍历每个节点，校验节点值是否在指定目标范围内，如果在区间范围则不执行操作，如果不在区间范围则删除节点并更新树，这种情况下则需要遍历每个节点并更新（且需注意不可以改变原有树的结构），复杂度较高

可以充分借助二叉搜索树的特性，基于剪枝的概念去处理（找到第1个满足区间要求的节点，然后基于此节点分析其左右子节点）

① 遍历节点：找到第1个满足[low,high]区间范围内的节点cur
- cur==null：如果节点不存在，说明整棵树的节点都不在这个区间范围，相当于要将整颗树剪掉（return null）
- cur!=null：如果节点存在，则基于这个节点对其左右子树的情况进行剪枝（分别校验左、右子树）
② 基于cur节点，对左、右子树进行校验
- cur.left 与 low边界校验：
  - cur.left.val<low（超出边界）：当前节点cur.left需要被移除，其右节点上位（cur.left = cur.left.right）
    - 分析：因为cur.left已经越界，则cur.left.left只会更小，只能让cur.left.right覆盖cur.left达到有效裁剪目的，并等待下一次校验
  - cur.left.val>=low（覆盖边界）：继续下个左子节点遍历（根据二叉树特性，其右子节点也肯定满足>=low）
- cur.right 与 high边界校验：
  - cur.right.val>high（超出边界）：当前节点cur.right需要被移除，其左节点上位（cur.right= cur.right.left）
    - 分析：同理，因为cur.right已经越界，则cur.right.right只会更大，只能让cur.right.left覆盖cur.right达到有效裁剪目的，并等待下一次校验
  - cur.right.val<=high（覆盖边界）：继续下个右子节点遍历（根据二叉树特性，其左子节点也肯定满足<=high）

👻方法1：迭代法（掐头去尾：找到第1个满足区间要求的节点，然后基于此期间分别遍历其左右子树进行剪枝）

==核心思路：==找到第一个满足[L,R]区间的节点，剪枝左子树、剪枝右子树
思路分析：顺序迭代遍历
- （1）找到第1个满足区间要求的节点cur
- （2）以cur为起点分别遍历其左右子树进行剪枝（根据左右子树根节点的值与边界条件的比较（超出边界、覆盖边界），区分需修剪的情况判断、指针移动的情况判断）
  - 左子树与low左边界的校验（此处leftNode指代cur.left，在算法处理的过程中需注意引用问题，直接在原树上修改）
    - leftNode.val<low（超出边界）：根据二叉搜索树的特性，则leftNode.left必然也会超出边界，因此此处剪枝直接剪掉leftNode和leftNode.left（即执行leftNode=leftNode.right）
    - leftNode>=low（覆盖边界）：则leftNode.right必然也会覆盖边界（表示leftNode和leftNode.right满足条件可以跳过校验），因此此处遍历节点切换到其左节点等待下一轮判断（即执行cur=cur.left）
  - 右子树与high右边界的校验
  - （此处rightNode指代cur.right，在算法处理的过程中需注意引用问题，直接在原树上修改）
    - rightNode.val>high（超出边界）：根据二叉搜索树的特性，则rightNode.right必然也会超出边界，因此此处剪枝直接剪掉rightNode和rightNode.right（即执行rightNode=rightNode.left）
    - rightNode<=high（覆盖边界）：则rightNode.left必然也会覆盖边界（表示rightNode和rightNode.left满足条件可以跳过校验），因此此处遍历节点切换到其左节点等待下一轮判断（即执行cur=cur.right）
- （3）迭代处理完成，最终返回cur（因为它是第一个满足区间条件的节点）
- 算法要点分析：
  - ==为什么左子树只需要校验左边界？右子树只需要校验右边界？==因为找到的第一个满足区间条件的节点cur已经满足[low,high]
    - 对于其左子树而言，所有的节点都只会比cur.val小，则自然满足<=high，因此只需要校验low边界
    - 同理，对于其右子树而言，所有的节点都只会比cur.val大，则自然满足>=low，因此只需要校验high边界
  - 如何理解掐头去尾？：
    - 所谓掐头：循环遍历找到第1个满足区间要求的节点cur（那么在这个满足条件的cur之前遍历的节点都不符合条件，也就不需要保留），因此最终返回的是这个cur为起点的子树，而非root
    - 所谓去尾：指的是当找到第1个满足区间要求的节点cur，需要分别迭代其左右子树（起点相同，遍历指针不同），根据其是否会越过边界（low\right），来进一步做相应的剪枝或指针移动处理
      - 超出边界 =》剪枝处理
      - 未超出边界 =》说明值覆盖，则指针移动继续寻找下一个节点（指针移动的方向则看需要跳过哪些节点，继续往下走）

/**
 * 669 修剪二叉搜索树
 */
public class Solution2 {

    /**
     * 迭代法：
     * 1.找到符合节点值在[low,high]范围内的节点cur
     * 2.迭代处理该节点的左右子树（左右子树的处理逻辑是类似的,核心关注两点：需要剪枝的情况、指针移动的情况，且左右子树的遍历指针要分开，起点都是从cur开始）
     * - 2.1 分别处理左节点的左右子树（左节点校验部分负责左边界low校验），此处leftNode、rightNode指代node的左右节点，算法实现的时候需注意引用问题(原地修改，不要构建新节点处理，否则还要重新赋值一遍才生效)
     * - 2.1.a.如果leftNode.val<low(需修剪的情况)，则根据二叉搜索树特性，则leftNode.left的所有值肯定也是小于low。因此可以直接剪掉leftNode和leftNode.left，只保留leftNode.right(即leftNode = leftNode.right)
     * - 2.1.b.如果leftNode.val>=low（指针移动的情况），则leftNode.right的所有值肯定大于等于low，因此【跳过】这些节点，移动指针（即node=node.left），循此往复，将所有的情况都覆盖在这些取值讨论中，直到遍历节点为空，遍历结束
     * <p>
     * - 2.2 处理右子树（右节点校验部分负责high校验）
     * - 2.2.a.如果rightNode.val>high(需修剪的情况)，则该右节点的右子树的所有值肯定大于high，因此可以直接剪掉rightNode和rightNode.right(即rightNode=rightNode.left)
     * - 2.2.b.如果右节点rightNode.val<=high（指针移动的情况），则rightNode.left的所有值肯定小于等于high，因此【跳过】这些节点，移动指针（即node=node.right），循此往复，将所有的情况都覆盖在这些取值讨论中，直到遍历节点为空，遍历结束
     */
    public TreeNode trimBST(TreeNode root, int low, int high) {

        if (root == null) {
            return root;
        }

        TreeNode cur = root; // 定义遍历节点
        // 1.找到符合节点值在指定区间范围的节点
        while (cur != null) {
            if (low <= cur.val && cur.val <= high) {
                break; // 找到目标节点，退出循环
            } else if (cur.val < low) {
                cur = cur.right; // 遍历节点在区间左侧，需往右移动
            } else if (cur.val > high) {
                cur = cur.left; // 遍历节点在区间右侧，需往左移动
            }
        }

        // 2.判断这个节点是否存在，如果不存在则直接返回null（说明没有满足区间范围的节点，直接返回null），如果存在则分情况讨论进行剪枝
        if (cur == null) {
            return null;
        }

        // 2.1 符合区间范围的节点node存在，以这个节点为起点，分别进行左右子树的判断和剪枝操作
        TreeNode lPointer = cur; // 以当前节点为起点，遍历左子树
        while (lPointer.left != null) {
            // 根据当前节点的左节点leftNode的值与区间值左边界low的关系，进一步分析leftNode的左右子树和区间值的关系
            if (lPointer.left.val < low) {
                // 需要剪枝的情况(leftNode.left肯定<low可以直接剪，leftNode也可以剪，因此leftNode直接替换为其右节点)
                lPointer.left = lPointer.left.right; // 剪掉leftNode、leftNode.left
            } else {
                // leftNode.val >= low,则leftNode右子树一定符合条件，则继续遍历其左子树
                lPointer = lPointer.left; // 移动节点等待下一次剪枝判断
            }
        }

        // 2.2 同理，遍历右子树
        TreeNode rPointer = cur; // 以当前节点为起点，遍历右子树
        while (rPointer.right != null) {
            //  根据当前节点的右节点rightNode的值与区间值右边界high的关系，进一步分析rightNode的左右子树和区间值的关系
            if (rPointer.right.val > high) {
                // 需要剪枝的情况
                rPointer.right = rPointer.right.left; //rightNode.val > high满足，则rightNode.right.val > high肯定满足，因此直接剪掉rightNode.right、rightNode
            } else {
                // rightNode.val <= high，则rightNode左子树也一定符合条件，只需继续遍历其右子树
                rPointer = rPointer.right; // 移动节点等待下一次剪枝判断
            }
        }

        // 返回迭代后的节点信息（此处返回结果应以cur节点开始，前期遍历已经过滤掉不满足的节点记录了）
        return cur;
    }
}

复杂度分析
- 时间复杂度：
- 空间复杂度：

另一种写法版本参考：

/**
 * 669 修剪二叉搜索树
 */
public class Solution3 {

    /**
     * 迭代法
     */
    public TreeNode trimBST(TreeNode root, int low, int high) {

        if (root == null) {
            return root;
        }

        TreeNode cur = root; // 定义遍历节点
        // 1.找到符合节点值在指定区间范围的节点
        while (cur != null) {
            if (low <= cur.val && cur.val <= high) {
                break; // 找到目标节点，退出循环
            } else if (cur.val < low) {
                cur = cur.right; // 遍历节点在区间左侧，需往右移动
            } else if (cur.val > high) {
                cur = cur.left; // 遍历节点在区间右侧，需往左移动
            }
        }

        // 2.判断这个节点是否存在，如果不存在则直接返回null（说明没有满足区间范围的节点，直接返回null），如果存在则分情况讨论进行剪枝
        if (cur == null) {
            return null;
        }

        // 2.1 符合区间范围的节点node存在，以这个节点为起点，分别进行左右子树的判断和剪枝操作
        TreeNode lPointer = cur; // 以当前节点为起点，遍历左子树
        while (lPointer != null) {
            // 处理左孩子元素小于L的情况
            while (lPointer.left != null && lPointer.left.val < low) {
                // 需要剪枝的情况(leftNode.left肯定<low可以直接剪，leftNode也可以剪，因此leftNode直接替换为其右节点)
                lPointer.left = lPointer.left.right; // 剪掉leftNode、leftNode.left
            }
            lPointer = lPointer.left; // 移动节点等待下一次剪枝判断
        }

        // 2.2 同理，遍历右子树
        TreeNode rPointer = cur; // 以当前节点为起点，遍历右子树
        while (rPointer != null) {
            // 处理右孩子元素大于R的情况
            while (rPointer.right != null && rPointer.right.val > high) {
                rPointer.right = rPointer.right.left; //rightNode.val > high满足，则rightNode.right.val > high肯定满足，因此直接剪掉rightNode.right、rightNode
            }
            rPointer = rPointer.right; // 移动节点等待下一次剪枝判断
        }

        // 返回迭代后的节点信息（此处返回结果应以cur节点开始，前期遍历已经过滤掉不满足的节点记录了）
        return cur;
    }
}

👻方法2：递归法（DFS）

思路分析：基于深度优先遍历的思想
- 递归分析：根据当前访问节点值进行判断（此处拟设当前访问节点为node）
  - 如果node为空节点，则返回null
  - 如果node不为空，则判断节点值与边界的关系
    - 如果node.val<low，则说明其左节点都不符合要求（在low边界左侧，需排除），则返回对其右节点进行修剪后的结果
    - 如果node.val>high，则说明其右节点都不符合要求（在high边界右侧，需排除），则返回对其左节点进行修剪后的结果
    - 如果node的取值在[low,right]区间范围内，则递归设定node的左右节点，返回递归后的node

/**
 * 669 修剪二叉搜索树
 */
public class Solution1 {

    /**
     * 递归法：
     * 判断每个遍历节点的值与边界的关系，然后结合二叉搜索树的特性进行处理：
     * 1.如果node.val<low 则说明node及其左子树都会小于low（超出边界，需排除），这种情况下返回的是【node的右子树经过递归修剪后的结果】
     * 2.如果node.val>low 则说明node及其右子树都会大于high（超出边界，需排除），这种情况下返回的是【node的左子树经过递归修剪后的结果】
     * 3.如果node.val取值在[low,high]区间范围内，则递归处理其左右节点，返回【node】
     */
    public TreeNode trimBST(TreeNode root, int low, int high) {
        return dfsHelper(root, low, high);
    }

    // 构建辅助的dfs函数帮助处理树
    public TreeNode dfsHelper(TreeNode node, int low, int high) {
        // 递归出口
        if (node == null) {
            return null;
        }

        // 根据node.val与边界值的判断(超出边界则剪枝，未超出边界则构建左右节点)进行处理
        int curNodeVal = node.val;
        if (curNodeVal < low) {
            // 当前节点超出low边界左侧，则其左子树也会超出low边界左侧，因此此处返回的是【node的右子树经过递归修剪后的结果】
            return dfsHelper(node.right, low, high);
        } else if (curNodeVal > high) {
            // 当前节点超出high边界右侧，则其右子树也会超出high边界右侧，因此此处返回的是【node的左子树经过递归修剪后的结果】
            return dfsHelper(node.left, low, high);
        } else {
            // low<=curNodeVal<=high的情况，正常递归处理左右节点
            node.left = dfsHelper(node.left, low, high);
            node.right = dfsHelper(node.right, low, high);
            return node;
        }
    }
}

复杂度分析
- 时间复杂度：
- 空间复杂度：

🟢将有序数组转化为二叉搜索树（108）

1.题目内容open in new window

给你一个整数数组 nums ，其中元素已经按升序排列，请你将其转换为一棵平衡二叉搜索树。

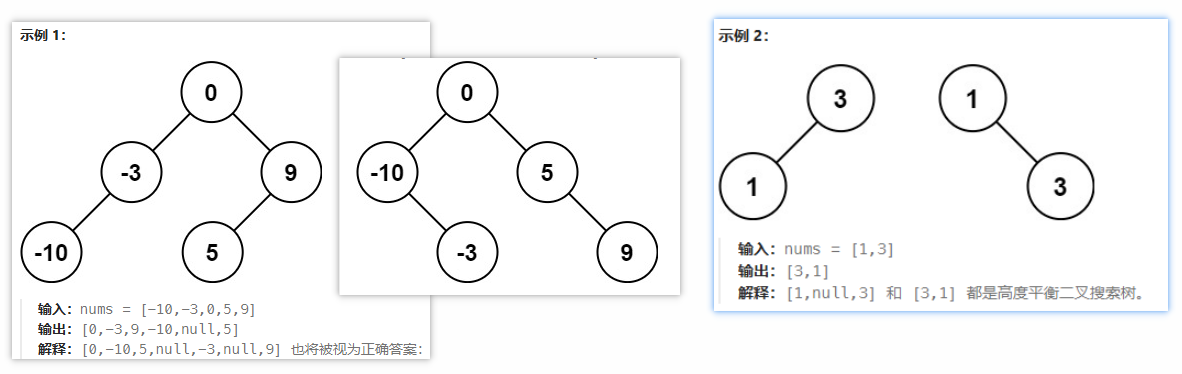
2.题解思路

👻方法1：递归法

思路分析：数组本身有序，因此将中间作为根节点，中间左侧作为左子树，中间右侧作为右子树，递归构建

public class Solution1 {
    // 递归构建
    public TreeNode sortedArrayToBST(int[] nums) {
        // 数组本身有序，指定构建区间（闭区间[left,right]）
        return buildHelper(nums,0,nums.length-1);
    }

    // 递归构建(DFS思路：DLR)
    public TreeNode buildHelper(int[] nums,int left,int right){
        // 如果边界越界则不符合，返回null
        if(left>right){
            return null;
        }

        // 构建node
        int mid = left + (right-left)/2;
        TreeNode node = new TreeNode(nums[mid]);
        // 递归构建左、右节点
        node.left = buildHelper(nums,left,mid-1);
        node.right = buildHelper(nums,mid+1,right);
        // 返回构建好的节点
        return node;
    }
}

复杂度分析
- 时间复杂度：
- 空间复杂度：

🟡将二叉搜索树转化为累加树（538）

1.题目内容open in new window

给出二叉搜索树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。

提醒一下，二叉搜索树满足下列约束条件：

节点的左子树仅包含键小于节点键的节点
节点的右子树仅包含键大于节点键的节点
左右子树也必须是二叉搜索树。

**注意：**本题和 1038: https://leetcode-cn.com/problems/binary-search-tree-to-greater-sum-tree/ 相同

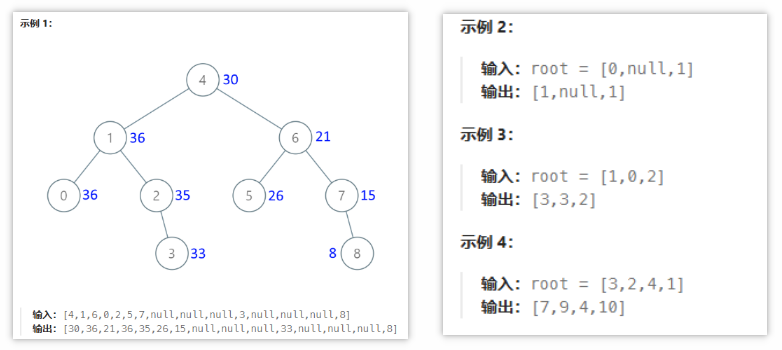
2.题解思路

👻方法1：反序中序遍历

思路分析：二叉搜索树的中序遍历是一个单调递增的有序序列，如果反序地中序遍历该二叉搜索树会得到一个单调递减的有序序列
- 题中核心在于将每个节点的值修改为原来的节点值加上所有大于它的节点值之和，因此可以将题意切换为【反序中序遍历+累加和回填节点值】的思路
  - 以上述【示例1】为例进行分析，中序遍历的结果是【1，2，3，4，5，6，7，8】，则其反序中序遍历的结果是RDL【8，7，6，5，4，3，2，1】
  - 而【累加和回填节点值】的概念指的是按照【反序中序遍历】的顺序遍历节点，然后每次对节点值进行累加作为当前节点的值，就能够满足题意。例如第一个遍历节点是8则其累加和为8进行回填，第二个遍历节点是7则其累加和是8+7=15进行回填。第三个遍历节点是6则其累加和是15+6=21进行回填.....以此类推
核心说明：
- ① 遍历顺序：逆序中序遍历（RDL遍历顺序）
- ② sum的定义：作为全局变量定义，整个递归周期过程中进行累加

/**
 * 538 把二叉搜索树转换为累加树
 */
public class Solution1 {

    int sum = 0; // 全局变量记录累加值

    // 反序中序遍历（迭代法思路）
    public TreeNode convertBST(TreeNode root) {
        dfsByRDL(root);
        return root;
    }

    public void dfsByRDL(TreeNode node) {
        // 递归出口
        if (node == null) {
            return;
        }

        // R
        dfsByRDL(node.right);

        // D: 结果累加并回填数值
        sum = sum + node.val;
        node.val = sum; // 回填累加值

        // L
        dfsByRDL(node.left);
    }

}

复杂度分析
- 时间复杂度：
- 空间复杂度：

栈写法

class Solution {
    public TreeNode convertBST(TreeNode root) {
        Deque<TreeNode> stack=new ArrayDeque<TreeNode>();
        int sum=0;
        TreeNode tmp=root;      
        while(!stack.isEmpty()||root!=null){
            while(root!=null){
                stack.push(root);
                root=root.right;
            }
            root=stack.pop();
            sum+=root.val;
            root.val=sum;
            root=root.left;
        }
        return tmp;
    }
}

🟡1382-将二叉搜索树变平衡

1.题目内容open in new window

给你一棵二叉搜索树，请你返回一棵 平衡后 的二叉搜索树，新生成的树应该与原来的树有着相同的节点值。如果有多种构造方法，请你返回任意一种。

如果一棵二叉搜索树中，每个节点的两棵子树高度差不超过 1 ，我们就称这棵二叉搜索树是 平衡的

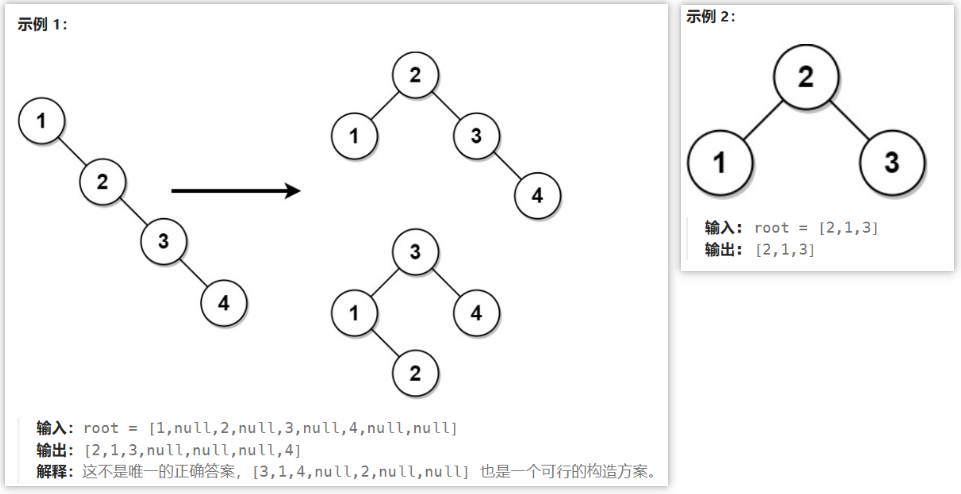
2.题解思路

👻方法1：转有序列表 + 构建平衡树

思路分析：
- 基于二叉搜索树的特性，思考如何构建一个平衡树。平衡树要求节点高度差不能超过1，因此借助二叉搜索树【中序遍历】后序列的有序性，基于这个序列去构建平衡树
- 回忆如何基于中序+后序、中序+前序复原二叉树，此处构建二叉树的思路也是类似的，首先确定根节点，然后确定左右子树，不断递归构建
  - 那么对于这个【有序列表】而言，每次都递归构建选择中点位置作为根节点，而其左右子树的列表也就确定下来了

/**
 * 🟡 1382 将二叉搜索树变平衡
 */
public class Solution1 {

    public TreeNode balanceBST(TreeNode root) {
        // 获取二叉搜索树中序遍历的结果(二叉搜索树中序遍历为有序列表)
        List<Integer> inorder = new ArrayList<>();
        dfs(root, inorder);
        // 根据中序遍历构建节点
        TreeNode newTreeRoot = buildHelper(inorder, 0, inorder.size() - 1);
        // 返回构建的平衡树
        return newTreeRoot;
    }

    // 中序遍历(LRD)
    public void dfs(TreeNode node, List<Integer> list) {
        // 递归出口
        if (node == null) {
            return;
        }
        dfs(node.left, list);
        list.add(node.val);
        dfs(node.right, list);
    }

    // 平衡树构建辅助函数
    public TreeNode buildHelper(List<Integer> inorder, int start, int end) {

        // 条件控制
        if (start > end) {
            return null;
        }

        // 构建根节点
        int mid = (end - start) / 2 + start;
        TreeNode node = new TreeNode(inorder.get(mid));
        // 构建左右节点
        node.left = buildHelper(inorder, start, mid - 1);
        node.right = buildHelper(inorder, mid + 1, end);

        // 返回构建节点
        return node;
    }

    public static void main(String[] args) {
        TreeNode node1 = new TreeNode(1);
        TreeNode node2 = new TreeNode(2);
        TreeNode node3 = new TreeNode(3);
        TreeNode node4 = new TreeNode(4);
        node1.right = node2;
        node2.right = node3;
        node3.right = node4;
        Solution1 s = new Solution1();
        s.balanceBST(node1);
    }

}

复杂度分析
- 时间复杂度：
- 空间复杂度：

🍚二叉树的公共祖先问题

🟡二叉树的最近公共祖先（236）

1.题目内容open in new window

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科open in new window中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

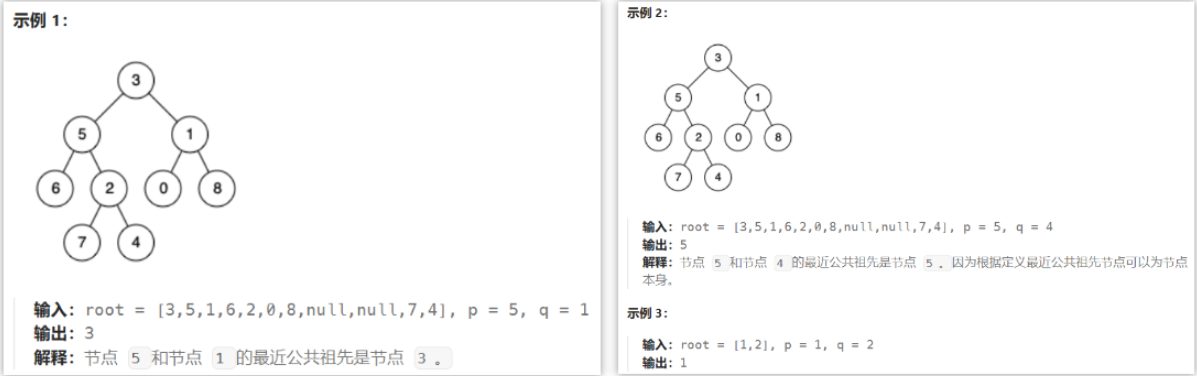
2.题解思路

👻方法1：分类讨论（递归处理）

思路分析：通过遍历每个节点，判断是不是最近公共祖先
- ① 递归出口：node==null || node==p || node==q：返回当前节点
- ② 递归遍历左右子树是否找到节点：如果左右子树都找到则返回当前节点，否则返回非null的那个子树（有可能两个都为null，找不到会通过递归出口退出）

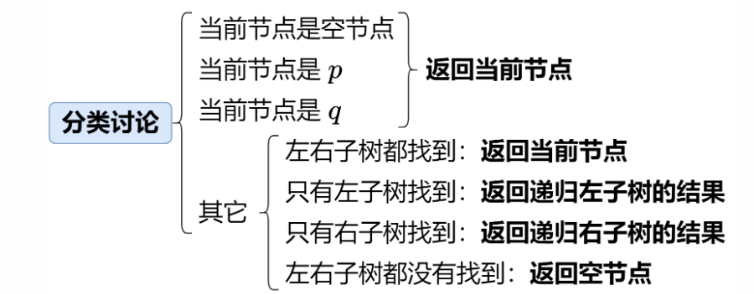
class Solution {
    // 递归思路，如果在过程中找到满足条件的直接返回
    public TreeNode lowestCommonAncestor(TreeNode node, TreeNode p, TreeNode q) {
        // 递归出口
        if (node == null || node == p || node == q) {
            return node; // node为null 或者 node为p、q中的其中一个节点，则当前节点就是最近公共祖先
        }

        // 分别递归查找左右子树的最近公共祖先
        TreeNode leftNode = lowestCommonAncestor(node.left, p, q);
        TreeNode rightNode = lowestCommonAncestor(node.right, p, q);

        // 根据左右子树查找结果来确定最近公共祖先

        // 如果左、右子树都找到了，则当前节点就是最近公共祖先
        if (leftNode != null && rightNode != null) {
            return node;
        }

        // 如果左右子树都没有找到，则返回null
        if (leftNode == null && rightNode == null) {
            return null;
        }

        // 如果左子树或者右子树找到了，则返回找到的那个
        return leftNode != null ? leftNode : rightNode;
    }
}

复杂度分析
- 时间复杂度：O(n) 需遍历所有节点，n为节点个数
空间复杂度：取决于递归的深度

🟡二叉搜索树的最近公共祖先（235）

1.题目内容open in new window

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科open in new window中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

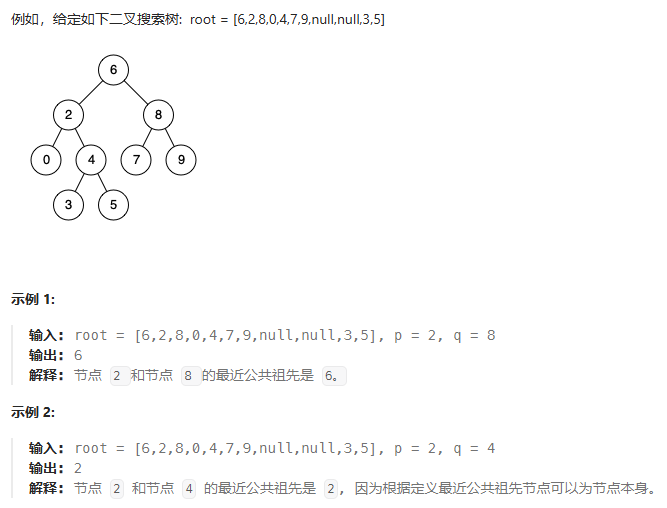
2.题解思路

二叉搜索树可以理解为特殊的二叉树，因此直接用【236-二叉树的最近公共祖先】的通用解法也可以处理，但此处更多考察的是二叉搜索树的特性，要结合二叉搜索树的特性去优化算法效率

对比普通的【二叉树的最近公共祖先问题】，此处要充分利用二叉搜索树的特性（有序树）。二叉搜索树的最近祖先问题比普通二叉树的最近祖先问题要简单，它不需要使用回溯，而是借助二叉搜索树的有序性可以方便地自上而下查找目标区间，遇到目标区间的节点直接返回。递归过程说明如下：

如果目标节点值在[p,q]或者[q,p]区间内，则直接直接返回该节点
如果目标节点值都比p、q大，则递归左子树（往左边走让值变小才有可能靠近最近祖先**（目标区间在左边）**）
如果目标节点值都比p、q大，则递归右子树（往右边走让值变小才有可能靠近最近祖先**（目标区间在右边）**）

如果中间节点是p、q的公共祖先，那么这个中间节点的数值一定是在[p,q]区间（即满足p<cur<q或q<cur<p），但需注意思考一个问题这个公共祖先一定是最近公共祖先吗？

结合图示理解，从上往下遍历节点：结合【图1】当遍历到5这个位置的时候满足区间位置1<5<9，如果说此时5在继续往下找，则可能会导致错过p或者q节点，因此此时5继续往下走是不合适的（走了3遇不到q、走了8遇不到p），也就是说节点自顶向下找到的第1个满足区间的节点一定是最近公共祖先

结合【图2】理解，从第1个节点开始查找：10（不在[6,9]区间内，且比p、q都大，会继续递归左子树查找），到了节点5（不在[6,9]区间内，且比p、q都小，会继续递归右子树查找），到了节点8找到目标

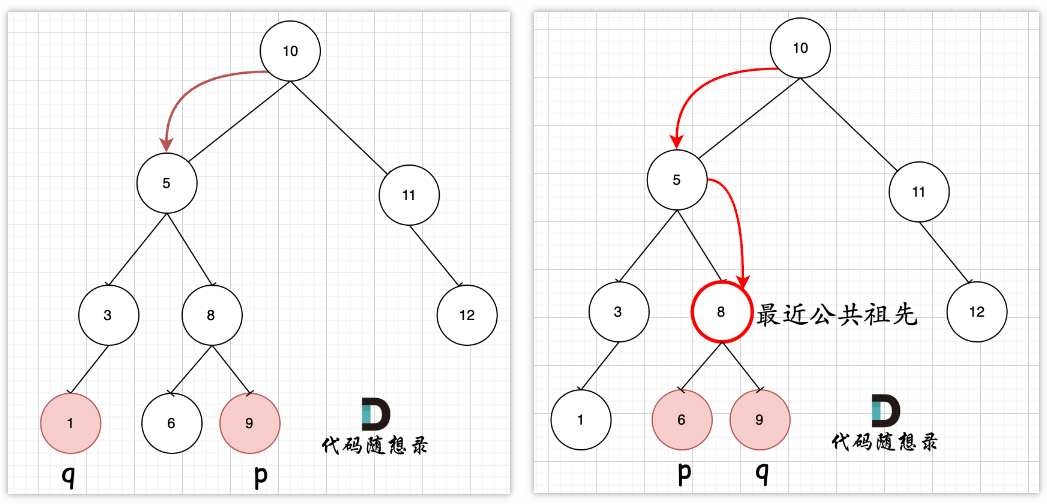
👻方法1：递归法

递归核心：当递归节点值在p、q区间内，则找到这个最近公共祖先。如果节点值均小于p、q则递归遍历左子树，如果节点值均大于p、q则递归遍历右子树

递归出口：node==null=>return null
递归判断：判断当前遍历节点的val与 p、q 的val值（此处无法明确 p、q 的值大小，因此要覆盖两种情况）
- ① curVal∈[p,q] 或者 curVal∈[q,p]：返回当前节点return node
- ② curVal均小于p、q节点的值，则最近公共子节点在右子树：return dfs(node.right, p, q)
- ③ curVal均大于p、q节点的值，则最近公共子节点在左子树：return dfs(node.left, p, q)

/**
 * 235 二叉搜索树的最近公共祖先
 */
public class Solution1 {

    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        return dfs(root, p, q);
    }

    // 深度优先遍历
    public TreeNode dfs(TreeNode node, TreeNode p, TreeNode q) {
        if (node == null) {
            return null;
        }
        // 如果当前节点值均大于p、q，则递归左子树（往左找才可能靠近p、q）
        if (node.val > p.val && node.val > q.val) {
            return dfs(node.left, p, q);
        }

        // 如果当前节点值均小于p、q，则递归右子树（往右找才可能靠近p、q）
        if (node.val < p.val && node.val < q.val) {
            return dfs(node.right, p, q);
        }

        // 如果当前节点值在指定区间[p,q]\[q,p]则返回当前节点
        return node;
    }
}

复杂度分析
- 时间复杂度：O（n）n为树节点个数
- 空间复杂度：取决于递归栈深度

👻方法2：迭代法

思路分析：从上往下遍历树节点，根据节点和p、q的关系选择要走的方向

/**
 * 235 二叉搜索树的最近公共祖先
 */
public class Solution2 {

    // 迭代法：
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if (root == null) {
            return null;
        }
        // 迭代
        TreeNode cur = root; // 定义遍历指针
        while (cur != null) {
            // 判断当前节点值和p、q的关系
            if (cur.val > p.val && cur.val > q.val) {
                cur = cur.left; // 当前值均大于p、q则往左子树方向走
            } else if (cur.val < p.val && cur.val < q.val) {
                cur = cur.right;// 当前值均小于p、q则往右子树方向走
            } else {
                return cur; // 当前值满足区间范围，即为所得
            }
        }
        // 没有找到目标
        return null;
    }

}

复杂度分析
- 时间复杂度：O（n）n为树节点个数
- 空间复杂度：O（1）

✨二叉树补充题型

🟡129-求根到叶子节点数字之和

1.题目内容

给你一个二叉树的根节点 root ，树中每个节点都存放有一个 0 到 9 之间的数字。

每条从根节点到叶节点的路径都代表一个数字：

例如，从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。

计算从根节点到叶节点生成的 所有数字之和 。

叶节点 是指没有子节点的节点。

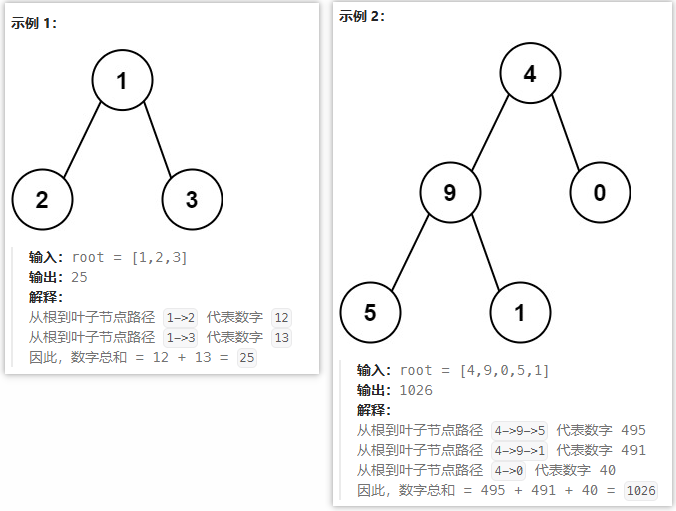
2.题解思路

bfs、dfs、回溯等方法

👻方法1：BFS

思路分析：基于BFS的思路
- 构建两个队列辅助遍历，nodeQueue（遍历节点）、valQueue（与对应遍历节点对照的节点值，表示当前路径节点构成的数字）
  - 结合上述案例分析，对于【图示1】中的节点来说，【节点1】的构成数字为1，而【节点2】的构成数字为12、【节点3】的构成数字为13，可以在分层遍历的过程中获取到相应的数字并填充
  - 当遍历到每个节点，校验其是否为叶子节点，如果为叶子节点则输出，这点实际上和【路径总和】的处理方向类似

/**
 * 🟡 129 求根节点到叶节点数字之和
 */
public class Solution2 {

    // BFS 思路
    public int sumNumbers(TreeNode root) {
        if (root == null) {
            return 0;
        }
        // 构建队列辅助遍历
        Queue<TreeNode> nodeQueue = new LinkedList<>(); // 存储对应节点
        nodeQueue.offer(root);
        Queue<Integer> valQueue = new LinkedList<>(); // 存储对应的值（拼接值）
        valQueue.offer(root.val);

        // 定义结果
        int res = 0;

        // 遍历节点
        while (!nodeQueue.isEmpty()) {
            // 分层遍历处理
            int cnt = nodeQueue.size();
            while (cnt-- > 0) {
                // 取出节点
                TreeNode curNode = nodeQueue.poll();
                int curNodeVal = valQueue.poll(); // 从valQueue队列中取出节点值（注意此处并非curNode.val）

                // 节点处理：如果curNode为叶子节点则累加叶子结点的和
                if (curNode.left == null && curNode.right == null) {
                    res += curNodeVal; // 累加叶子结点的值
                }

                if (curNode.left != null) {
                    nodeQueue.offer(curNode.left);
                    valQueue.offer(curNodeVal * 10 + curNode.left.val); // 将节点值进行拼接（与nodeQueue的入队节点保持同步）
                }
                if (curNode.right != null) {
                    nodeQueue.offer(curNode.right);
                    valQueue.offer(curNodeVal * 10 + curNode.right.val);// 将节点值进行拼接（与nodeQueue的入队节点保持同步）
                }
            }
        }

        // 返回结果
        return res;
    }
}

复杂度分析
- 时间复杂度：
- 空间复杂度：

👻方法2：回溯法

思路分析：可以基于【回溯模板】进行构建，可以通过断点调试确认算法处理逻辑是否正确
- 此处dfs并没有严格限定处理顺序，所以选择哪种dfs遍历顺序都可
- 此处对于路径的记录使用StringBuffer是因为考虑到节点数值只能为正数且节点取值范围为[0,9]，所以可以直接通过拼接的方式来处理构成的数字（替代原有的int数位处理），如果是其他情况下的节点，则还是需要用int接收处理

/**
 * 🟡 129 求根节点到叶节点数字之和
 */
public class Solution3 {

    // List<Integer> res = new ArrayList<>(); // 记录所有路径构成的数字的和（可以记录每个叶子结点的值加入列表，或者直接累加得到结果）
    int res = 0;
    StringBuffer path = new StringBuffer(); // 记录遍历路径构成的数字

    // 回溯法
    public int sumNumbers(TreeNode root) {
        if (root == null) {
            return 0;
        }
        // 初始化
        path.append(root.val); // 将根节点加入路径
        // 调用dfs
        dfs(root);
        // 返回结果
        return res;
    }

    // 递归处理
    public void dfs(TreeNode node) {
        // 递归出口
        if (node == null) {
            return;
        }
        // 如果是叶子结点则处理结果
        if (node.left == null && node.right == null) {
            int curPathVal = Integer.valueOf(path.toString()); // 将字符串数字转化为int类型
            res += curPathVal; // 累加结果(或者将路径节点值加入结果集合)
        }

        /**
         * 递归处理（回溯处理）
         * for(路径选择列表){
         *    ①处理节点
         *    ②调用递归
         *    ③回溯（恢复现场）
         * }
         * 此处的选择列表实际为`左节点`、`右节点`
         */
        if (node.left != null) {
            path.append(node.left.val); // 处理节点
            dfs(node.left); // 递归
            path.deleteCharAt(path.length() - 1); // 恢复现场
        }

        if (node.right != null) {
            path.append(node.right.val); // 处理节点
            dfs(node.right); // 递归
            path.deleteCharAt(path.length() - 1); // 恢复现场
        }
    }
}

复杂度分析
- 时间复杂度：
- 空间复杂度：

🔴 968-监控二叉树

1.题目内容

给定一个二叉树，我们在树的节点上安装摄像头。

节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。

计算监控树的所有节点所需的最小摄像头数量。

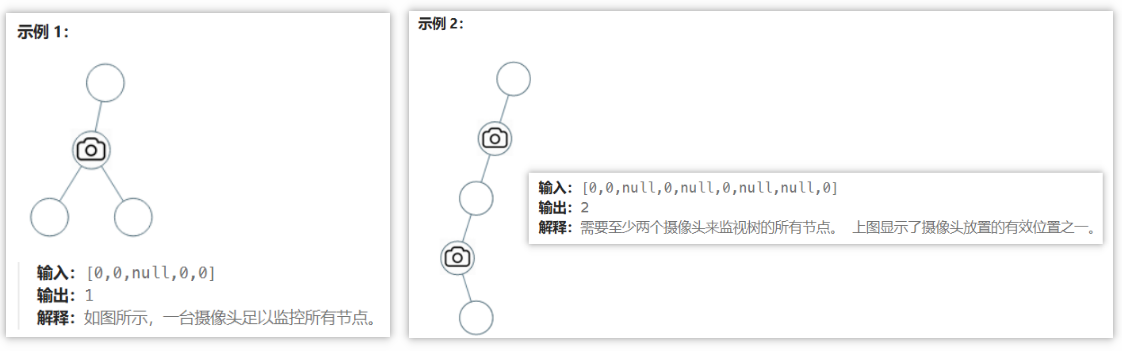
提示：

给定树的节点数的范围是 [1, 1000]
每个节点的值都是 0

2.题解思路

👻方法1：DFS

基于二叉树背景，联想到递归方式求解，关注如何根据左、右子树的状态推导出父节点的状态。此处约定如果某棵树的所有节点都被监控，则称该树被覆盖。

假设当前节点为root，其左、右孩子分别为left、right，如果要覆盖以root为根的树，则右两种情况：

① 若在root处放置摄像头，则其left、right也一定会被监控到，因此如果要设置最少的监控数量，则此处只需确保left和right其各自的两棵子树也被覆盖到即可
② 若不在root处放置摄像头，除了需要覆盖root的两棵子树之外，其孩子节点left、right之一必须有一个安装摄像头，以确保root被监控到

基于上述分析，对于每个节点root需要维护三种类型的状态，这三种状态会作为下一步的递推基础：

① 状态a：root必须放置摄像头的情况下，覆盖整棵树所需的摄像头数量
② 状态b：覆盖整棵树需要的摄像头数目，无论 root 是否放置摄像头（区分放与不放，选择min值）
③ 状态c：覆盖两棵子树需要的摄像头数目，无论节点 root 本身是否被监控到

基于上述定义，存在a≥b≥c的关系（因为条件越来越松）。而对于节点root而言，设其左右孩子 left,right 对应的状态变量分别为（l_a，l_b，l_c）、（r_a，r_b，r_c），结合上述分析可以得到求解a、b的过程：

① a = l_c + r_c + 1 （表示root处放置摄像头加上确保left、right各自的两棵子树也被覆盖的数量）

② b = min{a，min{l_a + r_b，r_a + l_b }} （区分放、不放的两种情况，选择min值）：

放：如果选择放，则与a状态一致
不放：如果选择不放，则为了确保其被覆盖，则需选择左或者右节点进行放置，这种情况下则取min{ l_a + r_b，r_a + l_b }

对于c而言，要保证两棵子树被完全覆盖，要么root处放置一个摄像头，需要的摄像头数量为 a ；要么root处不放置摄像头，让两棵子树自行分别保证自己被覆盖，需要的摄像头数量为l_b + r_b （区分放、不放的两种情况，选择min值）

③ c = min{ a，l_b + r_b}

此外，需要额外注意的是，对于root而言，如果其某个孩子为空，则不能通过在该孩子处放置摄像头的方式监控到当前节点，因此该孩子对应的变量a应该返回一个MAX_INTEGER，以用于表示不可能的情形。

最终，根节点的状态变量b即为所求。基于上述分析，按部就班计算每个节点的三种状态，当递归遍历结束返回b状态即为所得，参考代码分析如下所示

/**
 * 🔴 968 监控二叉树 - https://leetcode.cn/problems/binary-tree-cameras/submissions/592840411/
 */
public class Solution1 {

    public int minCameraCover(TreeNode root) {
        // 调用递归方法获取状态
        int[] arr = dfs(root);
        // 返回最终的b状态即为所得
        return arr[1];
    }


    // 递归处理
    public int[] dfs(TreeNode node) {
        if (node == null) {
            return new int[]{Integer.MAX_VALUE / 2, 0, 0}; // 除2用于防止加法溢出
        }

        int[] leftArr = dfs(node.left);
        int[] rightArr = dfs(node.right);

        // 分别处理当前节点的3种状态
        int a = leftArr[2] + rightArr[2] + 1;
        int b = Math.min(a, Math.min(leftArr[0] + rightArr[1], leftArr[1] + rightArr[0]));
        int c = Math.min(a, leftArr[1] + rightArr[1]);
        return new int[]{a, b, c};
    }

}

复杂度分析
- 时间复杂度：O（n）n 为二叉树节点个数，每个节点都会递归1次
- 空间复杂度：O（n）最坏情况下，二叉树是一条链，递归需要O（n）的栈空间

🟢543-二叉树的直径

1.题目内容open in new window

给你一棵二叉树的根节点，返回该树的直径。

二叉树的直径是指树中任意两个节点之间最长路径的长度。这条路径可能经过也可能不经过根节点 root 。

两节点之间路径的长度由它们之间边数表示

2.题解思路

👻方法1：DFS

核心：左右子树深度之和就是经过当前节点的当前最大直径，基于分拆思路，因此可以遍历每个节点，在递归遍历的同时去更新比较每个节点最大直径的值以通过局部推导全局

思路分析：依次遍历每个节点，将每个节点当做当前的子树root，然后调用depth递归方法获取左右子树的最大深度，并更新lrd+rrd的最大值

结合题目描述分析，如果要获取二叉树中任意两个节点的最大直径，则需要观察哪两个节点是最值得计算的？

以3个节点的二叉树为例：leftNode左子节点、rootNode根节点、rightNode右子节点，基于此计算最大直径：可能的最大直径 = leftNode到rootNode的距离（lrd） + rootNode到rightNode的距离（rrd），那么如何让这个lrd和rrd之和倾向最大则可得到max

如果说二叉树不限于这3个节点，当节点很多的情况下，二叉树的层级会越来越深，据此可以观察到，只要找到lrd+rrd的最大值即可，基于此回归深度遍历计算树的最大深度概念，在递归的过程就就去计算lrd+rrd的最大值

误区分析：此处可能存在一个容易出错的地方，结合上述公式分析，可能会误认为经过root的路径是最大的，所以将思路转向计算root的左右子树的最大深度之和，但实际上这个任意节点之间的最大直径可能并不会经过root（例如下述图示的节点参考）。因此此处的设定应该是当遍历到每个节点时，将其当做主节点记录下其左右子树的最大深度之和（即每个节点都有可能是上面的root角色），因此在迭代过程中就依次去对比lrd+rrd的最大值，然后所有节点遍历结束得到一个max

参考下述图示，如果基于图示代码拆分为左右子树（经过root）则得到最大值是1+6=7，而实际上当不经过root时有一条路径能得到8

/**
 * 🟢 543.二叉树直径 - https://leetcode.cn/problems/diameter-of-binary-tree/description/
 */
public class Solution1 {

    // 定义直径
    int diameter = 0;

    public int diameterOfBinaryTree(TreeNode root) {
        depth(root);
        return diameter;
    }

    // 定义计算树的最大深度方法
    public int depth(TreeNode node){
        if(node == null){
            return 0;
        }
        // 计算左子树
        int leftDepth = depth(node.left);
        // 计算右子树深度
        int rightDepth = depth(node.right);
        // 更新最大值(经过当前的最长直径即为左、右子树的深度，在递归求左右子树的深度的同时更新最大执行)
        diameter = Math.max(diameter, leftDepth + rightDepth);
        // 返回子树深度
        return Math.max(leftDepth, rightDepth) + 1;
    }

}

复杂度分析
- 时间复杂度：
- 空间复杂度：

🔴124-二叉树中的最大路径和

1.题目内容open in new window

二叉树中的路径被定义为一条节点序列，序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点

路径和 是路径中各节点值的总和

给你一个二叉树的根节点 root ，返回其 最大路径和

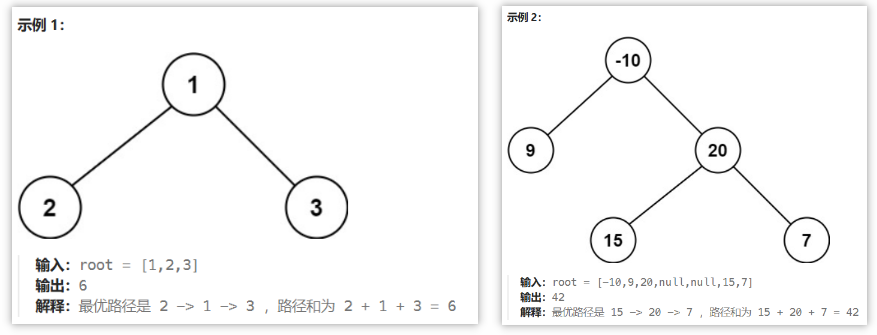
2.题解思路

👻方法1：结合【543-二叉树的最长直径】题思路进行分析

概念补充
- 链：从下面的某个节点（不一定是叶子）到当前节点的路径。把这条链的节点值之和，作为 dfs 的返回值。如果节点值之和是负数，则返回 0
- 直径：等价于由两条（或者一条）链拼成的路径。枚举每个 node，假设直径在这里「拐弯」，也就是计算由左右两条从下面的某个节点（不一定是叶子）到 node 的链的节点值之和，去更新答案的最大值

/**
 * 🔴 124 二叉树中的最大路径和
 */
public class Solution1 {

    public int maxSum = Integer.MIN_VALUE;

    public int maxPathSum(TreeNode root) {
        // 调用递归方法
        dfs(root);
        // 返回结果
        return maxSum;
    }

    // 递归处理（dfs返回的是链的节点值之和，而不是直径的节点值之和）
    private int dfs(TreeNode node) {
        if (node == null) {
            return 0; // 没有节点，和为0
        }

        // 计算左子树的最大链和
        int L = dfs(node.left);

        // 计算右子树的最大链和
        int R = dfs(node.right);

        // 两条链拼成路径
        maxSum = Math.max(maxSum, L + R + node.val);

        // 返回当前子树最大链和，向上层调用返回（如果必须选当前节点）的一定是当前节点+max(左树,右树),不然上一级就无法连城一条线了
        return Math.max(Math.max(L, R) + node.val, 0);

    }
}

复杂度分析
- 时间复杂度：O(n)，其中 n 为二叉树的节点个数
- 空间复杂度：O(n)。最坏情况下，二叉树退化成一条链，递归需要 O(n) 的栈空间

复杂度分析
- 时间复杂度：
- 空间复杂度：

复杂度分析
- 时间复杂度：
- 空间复杂度：

昵称

邮箱

网址

按正序
按倒序
按热度