算法-基础篇-02-数据结构

holic-x...大约 21 分钟

算法-基础篇-02-数据结构

学习核心

数据结构分类（逻辑结构、物理结构）
- 按“逻辑结构”：线性结构、非线性结构
  - 线性数据结构：数组、链表、栈、队列、哈希表，元素之间是一对一的顺序关系
  - 非线性数据结构：树、堆、图、哈希表（非线性数据结构可以进一步划分为树形结构和网状结构）
    - 树形结构：树、堆、哈希表，元素之间是一对多的关系
    - 网状结构：图，元素之间是多对多的关系
- 按“物理结构”：连续、分散
数字编码：原码、反码、补码
字符编码（ASCII、GBK、Unicode、UTF-8）

学习资料

数据结构

1.数据结构分类

常见的数据结构包括数组、链表、栈、队列、哈希表、树、堆、图，它们可以从“逻辑结构”和“物理结构”两个维度进行分类

逻辑结构：线性与非线性

逻辑结构揭示了数据元素之间的逻辑关系。在数组和链表中，数据按照一定顺序排列，体现了数据之间的线性关系；而在树中，数据从顶部向下按层次排列，表现出“祖先”与“后代”之间的派生关系；图则由节点和边构成，反映了复杂的网络关系

如下图所示，逻辑结构可分为“线性”和“非线性”两大类。线性结构比较直观，指数据在逻辑关系上呈线性排列；非线性结构则相反，呈非线性排列

线性数据结构：数组、链表、栈、队列、哈希表，元素之间是一对一的顺序关系
非线性数据结构：树、堆、图、哈希表（非线性数据结构可以进一步划分为树形结构和网状结构）
- 树形结构：树、堆、哈希表，元素之间是一对多的关系
- 网状结构：图，元素之间是多对多的关系

物理结构：连续与分散

当算法程序运行时，正在处理的数据主要存储在内存中。结合图示分析，一个计算机内存条其中每个黑色方块都包含一块内存空间。可以将内存想象成一个巨大的 Excel 表格（类比概念，实际内存的工作机制更加复杂），其中每个单元格都可以存储一定大小的数据。

系统通过内存地址来访问目标位置的数据。计算机根据特定规则为表格中的每个单元格分配编号，确保每个内存空间都有唯一的内存地址。有了这些地址，程序便可以访问内存中的数据

内存是所有程序的共享资源，当某块内存被某个程序占用时，则通常无法被其他程序同时使用了。因此在数据结构与算法的设计中，内存资源是一个重要的考虑因素。比如，算法所占用的内存峰值不应超过系统剩余空闲内存；如果缺少连续大块的内存空间，那么所选用的数据结构必须能够存储在分散的内存空间内。

结合下图图示分析，物理结构反映了数据在计算机内存中的存储方式，可分为连续空间存储（数组）和分散空间存储（链表）。物理结构从底层决定了数据的访问、更新、增删等操作方法，两种物理结构在时间效率和空间效率方面呈现出互补的特点。

值得说明的是，所有数据结构都是基于数组、链表或二者的组合实现的。例如，栈和队列既可以使用数组实现，也可以使用链表实现；而哈希表的实现可能同时包含数组和链表

基于数组可实现：栈、队列、哈希表、树、堆、图、矩阵、张量（维度 ≥3 的数组）等
基于链表可实现：栈、队列、哈希表、树、堆、图等

链表在初始化后，仍可以在程序运行过程中对其长度进行调整，因此也称“动态数据结构”。数组在初始化后长度不可变，因此也称“静态数据结构”。值得注意的是，数组可通过重新分配内存实现长度变化，从而具备一定的“动态性”

2.基本数据类型

当谈及计算机中的数据时，一般会想到文本、图片、视频、语音、3D 模型等各种形式。尽管这些数据的组织形式各异，但它们都由各种基本数据类型构成。

基本数据类型是 CPU 可以直接进行运算的类型，在算法中直接被使用，主要包括以下几种

整数类型 byte、short、int、long
浮点数类型 float、double ，用于表示小数
字符类型 char ，用于表示各种语言的字母、标点符号甚至表情符号等
布尔类型 bool ，用于表示“是”与“否”判断

基本数据类型以二进制的形式存储在计算机中。一个二进制位即为 1 比特。在绝大多数现代操作系统中，1 字节（byte）由 8 比特（bit）组成。

基本数据类型的取值范围取决于其占用的空间大小，下面以 Java 为例

整数类型 byte 占用 1 字节 = 8 比特，可以表示 28 个数字
整数类型 int 占用 4 字节 = 32 比特，可以表示 232 个数字

此处列举了 Java 中各种基本数据类型的占用空间、取值范围和默认值

类型	符号	占用空间	最小值	最大值	默认值
整数	`byte`	1 字节	−2⁷ (−128)	2⁷−1 (127)	0
	`short`	2 字节	−2¹⁵	2¹⁵−1	0
	`int`	4 字节	−2³¹	2³¹−1	0
	`long`	8 字节	−2⁶³	2⁶³−1	0
浮点数	`float`	4 字节	1.175×10⁻³⁸	3.403×10³⁸	0.0f
	`double`	8 字节	2.225×10⁻³⁰⁸	1.798×10³⁰⁸	0.0
字符	`char`	2 字节	0	2¹⁶−1	0
布尔	`bool`	1 字节	false	true	false

每种编程语言都有各自的数据类型定义，它们的占用空间、取值范围和默认值可能会有所不同。

在 Python 中，整数类型 int 可以是任意大小，只受限于可用内存；浮点数 float 是双精度 64 位；没有 char 类型，单个字符实际上是长度为 1 的字符串 str
C 和 C++ 未明确规定基本数据类型的大小，而因实现和平台各异。表 3-1 遵循 LP64 数据模型open in new window，其用于包括 Linux 和 macOS 在内的 Unix 64 位操作系统
字符 char 的大小在 C 和 C++ 中为 1 字节，在大多数编程语言中取决于特定的字符编码方法，详见“字符编码”章节
即使表示布尔量仅需 1 位（0 或 1），它在内存中通常也存储为 1 字节。这是因为现代计算机 CPU 通常将 1 字节作为最小寻址内存单元

那么，基本数据类型与数据结构之间有什么联系呢？=> 基本数据类型提供了数据的“内容类型”，而数据结构提供了数据的“组织方式”

数据结构是在计算机中组织与存储数据的方式。这句话的主语是“结构”而非“数据”。如果想表示“一排数字”，自然会想到使用数组。这是因为数组的线性结构可以表示数字的相邻关系和顺序关系，但至于存储的内容是整数 int、小数 float 还是字符 char ，则与“数据结构”无关。

例如以下代码，使用相同的数据结构（数组）来存储与表示不同的基本数据类型，包括 int、float、char、bool 等

// 使用多种基本数据类型来初始化数组
int[] numbers = new int[5];
float[] decimals = new float[5];
char[] characters = new char[5];
boolean[] bools = new boolean[5];

3.数字编码

原码、反码、补码

结合前面JAVA基本数据类型表格分析，所有整数类型能够表示的负数都比正数多一个，例如 byte 的取值范围是 [−128,127] 。这个现象比较反直觉，它的内在原因涉及原码、反码、补码的相关知识。首先需要指出，数字是以“补码”的形式存储在计算机中的。在分析这样做的原因之前，首先给出三者的定义

原码：将数字的二进制表示的最高位视为符号位，其中 0 表示正数，1 表示负数，其余位表示数字的值
反码：正数的反码与其原码相同，负数的反码是对其原码除符号位外的所有位取反
补码：正数的补码与其原码相同，负数的补码是在其反码的基础上加 1

问题1：为什么要引入补码？

原码虽然直观，但具备局限性（负数的原码不能直接用于运算）。例如在原码中计算 1 +（-2）得到 -3 这显然是错误的

 1+（-2）
-> 0000 0001 + 1000 0010
=  1000 0011
= -3 (错误)

引入反码：
- 为了解决负数运算问题，计算机引入了反码。如果先将原码转为反码，并在反码下进行计算，然后再将结果转回原码，则可得到正确结果 -1
```
 1+（-2）
-> 0000 0001(原码) + 1000 0010(原码)
=  0000 0001(反码) + 1111 1101(反码) （整数原码和反码相同、负数的反码除符号位外其他按位与原码取反）
=  1111 1110(反码)
=  1000 0001
= -1 (正确)
```
- 但如果使用反码，和原码一样存在正负零歧义问题（如果想处理+0、-0的歧义，则需引入额外的判断操作，可能会降低计算机的运算效率）
```
# 0 的原码有 +0 和 -0 的区分
+0 -> 0000 0000
-0 -> 1000 0000
# 同理 反码也存在正负零歧义问题
```

引入补码：

为了解决“正负零歧义”问题，计算机引入了补码

# 0 的原码有 +0 和 -0 的区分
+0 -> 0000 0000
-0 -> 1000 0000
# 0 的补码
+0 -> 0000 0000(补码)
-0 -> 1000 0000(原码)
   -> 1111 1111(反码)
   -> 1 0000 0000(补码) 在反码基础上+1 会产生进位，但byte长度只有8位，因此溢出到第9位的1会被舍弃
   -> 0000 0000(得到-0最终的补码) =》负零和正零的补码相同，意味着在补码中只存在1个零，进而解决了正负零歧义问题

问题2：byte 的取值范围是[-128,127]，多出来的这个-128是如何得到？

区间[-127,127]内所有整数都有其对应的原码、反码、补码，并且原码和补码之间可以相互转换。

计算机把1000 0000这个特殊的补码代表-128，虽然补码1000 0000代表的数值是-128，但是由于原码和反码的定义存在缺陷，通过传统的“取反加1”的思路求-128的原码是不适用的。正常来说按照转化规则来说，它的反码为0111 1111，原码为0000 0000（但0000 0000原码是表示0的，显然是矛盾的）。实际上，-128：-1 + （-127）在补码计算下的结果就是-128

计算机内部的硬件电路主要是基于加法运算设计的。这是因为加法运算相对于其他运算（比如乘法、除法和减法）来说，硬件实现起来更简单，更容易进行并行化处理，运算速度更快。但这并不意味着计算机只能做加法。通过将加法与一些基本逻辑运算结合，计算机能够实现各种其他的数学运算。例如，计算减法 a−b 可以转换为计算加法 a+(−b) ；计算乘法和除法可以转换为计算多次加法或减法。

计算机使用补码的原因：基于补码表示，计算机可以用同样的电路和操作来处理正数和负数的加法，不需要设计特殊的硬件电路来处理减法，并且无须特别处理正负零的歧义问题。这大大简化了硬件设计，提高了运算效率。

浮点数编码

问题：int 和 float 长度相同，都是4字节，为什么float的取值范围远大于int

正常思路分析来看，float因为需要表示小数，在相同的长度限制下，取值范围应该变小才对，为什么float的取值范围还远大于int =》 因为浮点数 float 采用了不同的表示方式

float 的表示方式包含指数位，导致其取值范围远大于 int 。根据以上计算，float 可表示的最大正数为 2^254−127×(2−2⁻²³)≈3.4×10³⁸ ，切换符号位便可得到最小负数。

尽管浮点数 float 扩展了取值范围，但其副作用是牺牲了精度。整数类型 int 将全部 32 比特用于表示数字，数字是均匀分布的；而由于指数位的存在，浮点数 float 的数值越大，相邻两个数字之间的差值就会趋向越大。

4.字符编码

在计算机中，所有数据都是以二进制数的形式存储的，字符 char 也不例外。为了表示字符，需要建立一套“字符集”，规定每个字符和二进制数之间的一一对应关系。有了字符集之后，计算机就可以通过查表完成二进制数到字符的转换

ASCII字符集

ASCII 码是最早出现的字符集，其全称为 American Standard Code for Information Interchange（美国标准信息交换代码）。它使用 7 位二进制数（一个字节的低 7 位）表示一个字符，最多能够表示 128 个不同的字符。ASCII 码包括英文字母的大小写、数字 0 ~ 9、一些标点符号，以及一些控制字符（如换行符和制表符）

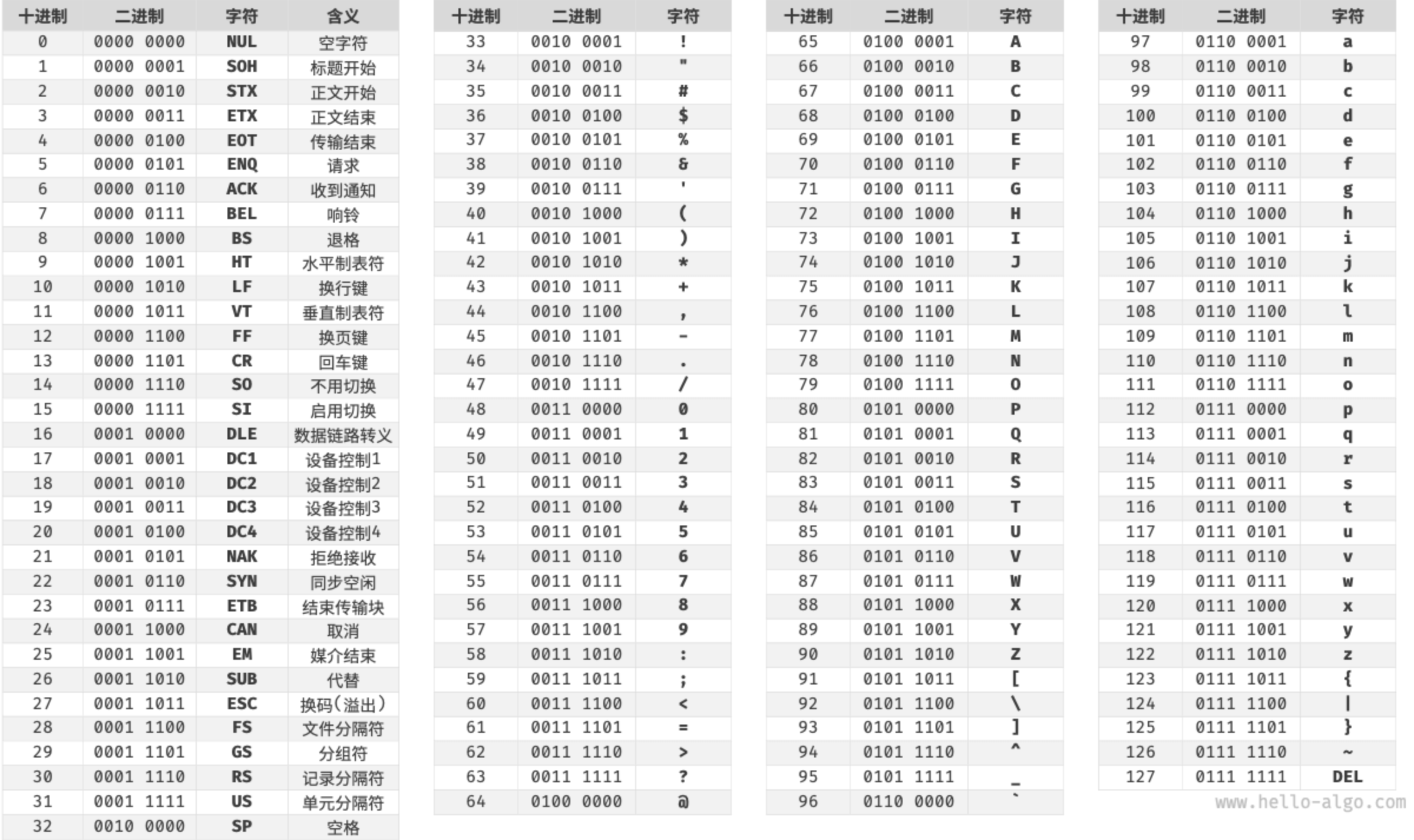
然而，ASCII 码仅能够表示英文。随着计算机的全球化，诞生了一种能够表示更多语言的 EASCII 字符集。它在 ASCII 的 7 位基础上扩展到 8 位，能够表示 256 个不同的字符。在世界范围内，陆续出现了一批适用于不同地区的 EASCII 字符集。这些字符集的前 128 个字符统一为 ASCII 码，后 128 个字符定义不同，以适应不同语言的需求。

GBK字符集

后来人们发现，EASCII 码仍然无法满足许多语言的字符数量要求。比如汉字有近十万个，光日常使用的就有几千个。中国国家标准总局于 1980 年发布了 GB2312 字符集，其收录了 6763 个汉字，基本满足了汉字的计算机处理需要。

然而，GB2312 无法处理部分罕见字和繁体字。GBK 字符集是在 GB2312 的基础上扩展得到的，它共收录了 21886 个汉字。在 GBK 的编码方案中，ASCII 字符使用一个字节表示，汉字使用两个字节表示。

Unicode 字符集

随着计算机技术的蓬勃发展，字符集与编码标准百花齐放，而这带来了许多问题。一方面，这些字符集一般只定义了特定语言的字符，无法在多语言环境下正常工作。另一方面，同一种语言存在多种字符集标准，如果两台计算机使用的是不同的编码标准，则在信息传递时就会出现乱码。

那个时代的研究人员就在想：如果推出一个足够完整的字符集，将世界范围内的所有语言和符号都收录其中，不就可以解决跨语言环境和乱码问题了吗？在这种想法的驱动下，一个大而全的字符集 Unicode 应运而生。

Unicode 的中文名称为“统一码”，理论上能容纳 100 多万个字符。它致力于将全球范围内的字符纳入统一的字符集之中，提供一种通用的字符集来处理和显示各种语言文字，减少因为编码标准不同而产生的乱码问题。

自 1991 年发布以来，Unicode 不断扩充新的语言与字符。截至 2022 年 9 月，Unicode 已经包含 149186 个字符，包括各种语言的字符、符号甚至表情符号等。在庞大的 Unicode 字符集中，常用的字符占用 2 字节，有些生僻的字符占用 3 字节甚至 4 字节。

Unicode 是一种通用字符集，本质上是给每个字符分配一个编号（称为“码点”），但它并没有规定在计算机中如何存储这些字符码点。思考一个问题：当多种长度的 Unicode 码点同时出现在一个文本中时，系统如何解析字符？例如给定一个长度为 2 字节的编码，系统如何确认它是一个 2 字节的字符还是两个 1 字节的字符？对于以上问题，一种直接的解决方案是将所有字符存储为等长的编码（位数不足高位填充）

然而 ASCII 码编码英文只需 1 字节。若采用上述方案，英文文本占用空间的大小将会是 ASCII 编码下的两倍，非常浪费内存空间。因此，需要一种更加高效的 Unicode 编码方法

UTF-8 编码

目前，UTF-8 已成为国际上使用最广泛的 Unicode 编码方法。它是一种可变长度的编码，使用 1 到 4 字节来表示一个字符，根据字符的复杂性而变。ASCII 字符只需 1 字节，拉丁字母和希腊字母需要 2 字节，常用的中文字符需要 3 字节，其他的一些生僻字符需要 4 字节。

UTF-8 的编码规则并不复杂，分为以下两种情况。

对于长度为 1 字节的字符，将最高位设置为 0 ，其余 7 位设置为 Unicode 码点。值得注意的是，ASCII 字符在 Unicode 字符集中占据了前 128 个码点。也就是说，UTF-8 编码可以向下兼容 ASCII 码。这意味着可以使用 UTF-8 来解析年代久远的 ASCII 码文本
对于长度为 n 字节的字符（其中 n>1），将首个字节的高 n 位都设置为 1 ，第 n+1 位设置为 0 ；从第二个字节开始，将每个字节的高 2 位都设置为 10 ；其余所有位用于填充字符的 Unicode 码点

图示展示了“Hello算法”对应的 UTF-8 编码。观察发现，由于最高 n 位都设置为 1 ，因此系统可以通过读取最高位 1 的个数来解析出字符的长度为 n 。但为什么要将其余所有字节的高 2 位都设置为 10 呢？

实际上，这个 10 能够起到校验符的作用。假设系统从一个错误的字节开始解析文本，字节头部的 10 能够帮助系统快速判断出异常。之所以将 10 当作校验符，是因为在 UTF-8 编码规则下，不可能有字符的最高两位是 10 。这个结论可以用反证法来证明：假设一个字符的最高两位是 10 ，说明该字符的长度为 1 ，对应 ASCII 码。而 ASCII 码的最高位应该是 0 ，与假设矛盾。

除了 UTF-8 之外，常见的编码方式还包括以下两种。

UTF-16 编码：使用 2 或 4 字节来表示一个字符。所有的 ASCII 字符和常用的非英文字符，都用 2 字节表示；少数字符需要用到 4 字节表示。对于 2 字节的字符，UTF-16 编码与 Unicode 码点相等。
UTF-32 编码：每个字符都使用 4 字节。这意味着 UTF-32 比 UTF-8 和 UTF-16 更占用空间，特别是对于 ASCII 字符占比较高的文本。

从存储空间占用的角度看，使用 UTF-8 表示英文字符非常高效，因为它仅需 1 字节；使用 UTF-16 编码某些非英文字符（例如中文）会更加高效，因为它仅需 2 字节，而 UTF-8 可能需要 3 字节。

从兼容性的角度看，UTF-8 的通用性最佳，许多工具和库优先支持 UTF-8

编程语言的字符编码

对于以往的大多数编程语言，程序运行中的字符串都采用 UTF-16 或 UTF-32 这类等长编码。在等长编码下，可以将字符串看作数组来处理，这种做法具有以下优点。

随机访问：UTF-16 编码的字符串可以很容易地进行随机访问。UTF-8 是一种变长编码，要想找到第 i 个字符，我们需要从字符串的开始处遍历到第 i 个字符，这需要 O(n) 的时间
字符计数：与随机访问类似，计算 UTF-16 编码的字符串的长度也是 O(1) 的操作。但是，计算 UTF-8 编码的字符串的长度需要遍历整个字符串
字符串操作：在 UTF-16 编码的字符串上，很多字符串操作（如分割、连接、插入、删除等）更容易进行。在 UTF-8 编码的字符串上，进行这些操作通常需要额外的计算，以确保不会产生无效的 UTF-8 编码

实际上，编程语言的字符编码方案设计是一个很有趣的话题，涉及许多因素。

Java 的 String 类型使用 UTF-16 编码，每个字符占用 2 字节。这是因为 Java 语言设计之初，人们认为 16 位足以表示所有可能的字符。然而，这是一个不正确的判断。后来 Unicode 规范扩展到了超过 16 位，所以 Java 中的字符现在可能由一对 16 位的值（称为“代理对”）表示。
JavaScript 和 TypeScript 的字符串使用 UTF-16 编码的原因与 Java 类似。当 1995 年 Netscape 公司首次推出 JavaScript 语言时，Unicode 还处于发展早期，那时候使用 16 位的编码就足以表示所有的 Unicode 字符了。
C# 使用 UTF-16 编码，主要是因为 .NET 平台是由 Microsoft 设计的，而 Microsoft 的很多技术（包括 Windows 操作系统）都广泛使用 UTF-16 编码。

由于以上编程语言对字符数量的低估，它们不得不采取“代理对”的方式来表示超过 16 位长度的 Unicode 字符。这是一个不得已为之的无奈之举。一方面，包含代理对的字符串中，一个字符可能占用 2 字节或 4 字节，从而丧失了等长编码的优势。另一方面，处理代理对需要额外增加代码，这提高了编程的复杂性和调试难度。

出于以上原因，部分编程语言提出了一些不同的编码方案。

Python 中的 str 使用 Unicode 编码，并采用一种灵活的字符串表示，存储的字符长度取决于字符串中最大的 Unicode 码点。若字符串中全部是 ASCII 字符，则每个字符占用 1 字节；如果有字符超出了 ASCII 范围，但全部在基本多语言平面（BMP）内，则每个字符占用 2 字节；如果有超出 BMP 的字符，则每个字符占用 4 字节。
Go 语言的 string 类型在内部使用 UTF-8 编码。Go 语言还提供了 rune 类型，它用于表示单个 Unicode 码点。
Rust 语言的 str 和 String 类型在内部使用 UTF-8 编码。Rust 也提供了 char 类型，用于表示单个 Unicode 码点。

需要注意的是，以上讨论的都是字符串在编程语言中的存储方式，这和字符串如何在文件中存储或在网络中传输是不同的问题。在文件存储或网络传输中，通常会将字符串编码为 UTF-8 格式，以达到最优的兼容性和空间效率。

昵称

邮箱

网址

按正序
按倒序
按热度

算法-基础篇-02-数据结构

预览: