算法-基础篇-02-数据结构-A(数组与链表)
算法-基础篇-02-数据结构-A(数组与链表)
学习核心
学习资料
数组
数组(array)是一种线性数据结构,其将相同类型的元素存储在连续的内存空间中。将元素在数组中的位置称为该元素的索引(index)。下图展示了数组的主要概念和存储方式
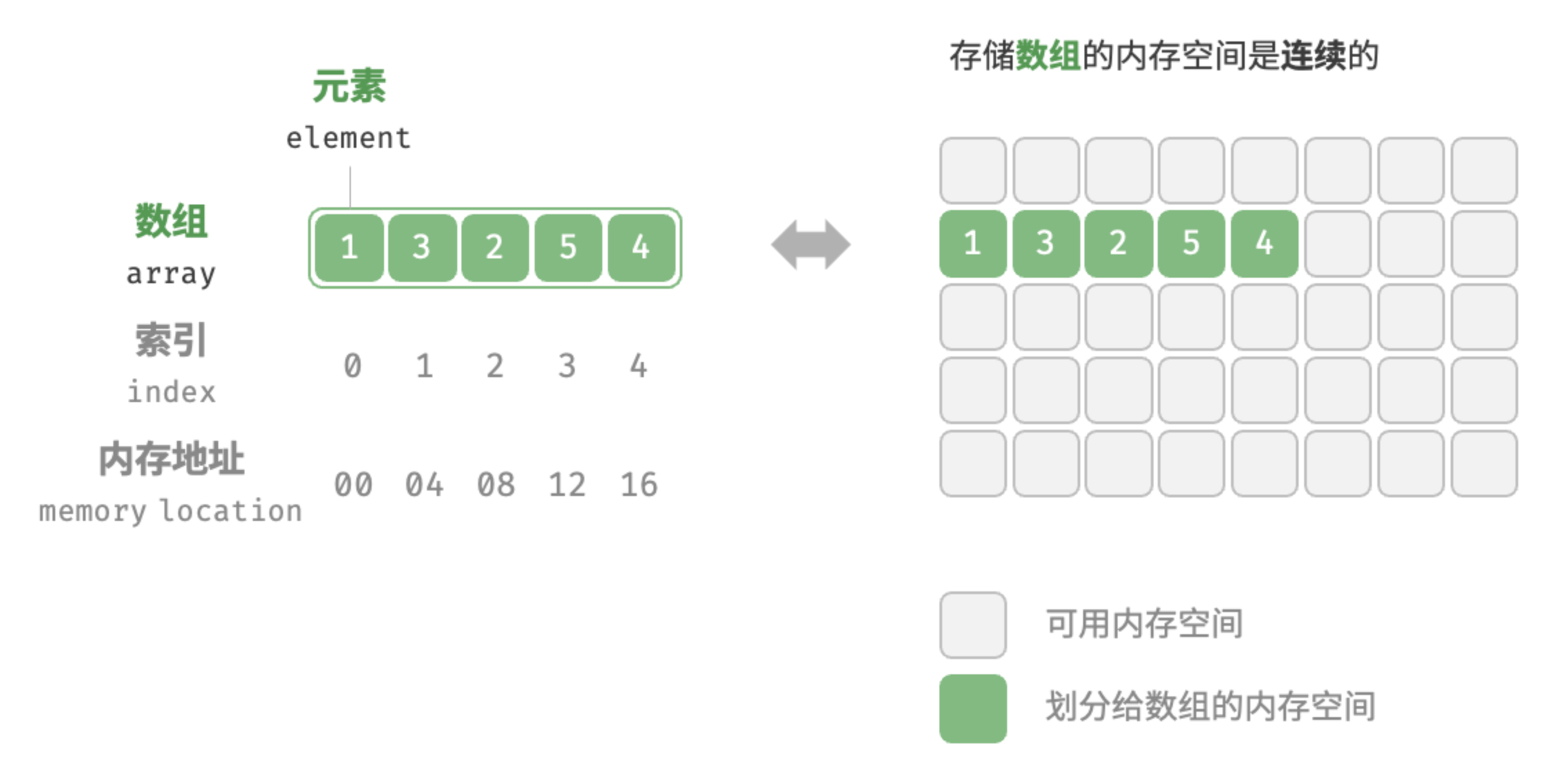
1.数组常用操作
初始化数组
可以根据需求选用数组的两种初始化方式:无初始值、给定初始值。
/* 初始化数组 */
int[] arr = new int[5]; // { 0, 0, 0, 0, 0 }
int[] nums = { 1, 3, 2, 5, 4 };
访问元素
数组元素被存储在连续的内存空间中,这意味着计算数组元素的内存地址非常容易。给定数组内存地址(首元素内存地址)和某个元素的索引,可以使用公式计算得到该元素的内存地址,从而直接访问该元素。在数组中访问元素非常高效,可以在 O(1) 时间内随机访问数组中的任意一个元素
.assets/image-20240814155635803.png)
问题:为什么数组首个元素的索引要设计为0?
正常情况下从1开始计数会更加自然,但从地址计算公式来看,索引本质上是内存地址的偏移量,首个元素的地址偏移量是 0 ,因此它的索引为 0 也是合理的。
插入元素
数组元素在内存中是“紧挨着的”,它们之间没有空间再存放任何数据。结合图示分析,如果想在数组中间插入一个元素,则需要将该元素之后的所有元素都向后移动一位,之后再把元素赋值给该索引
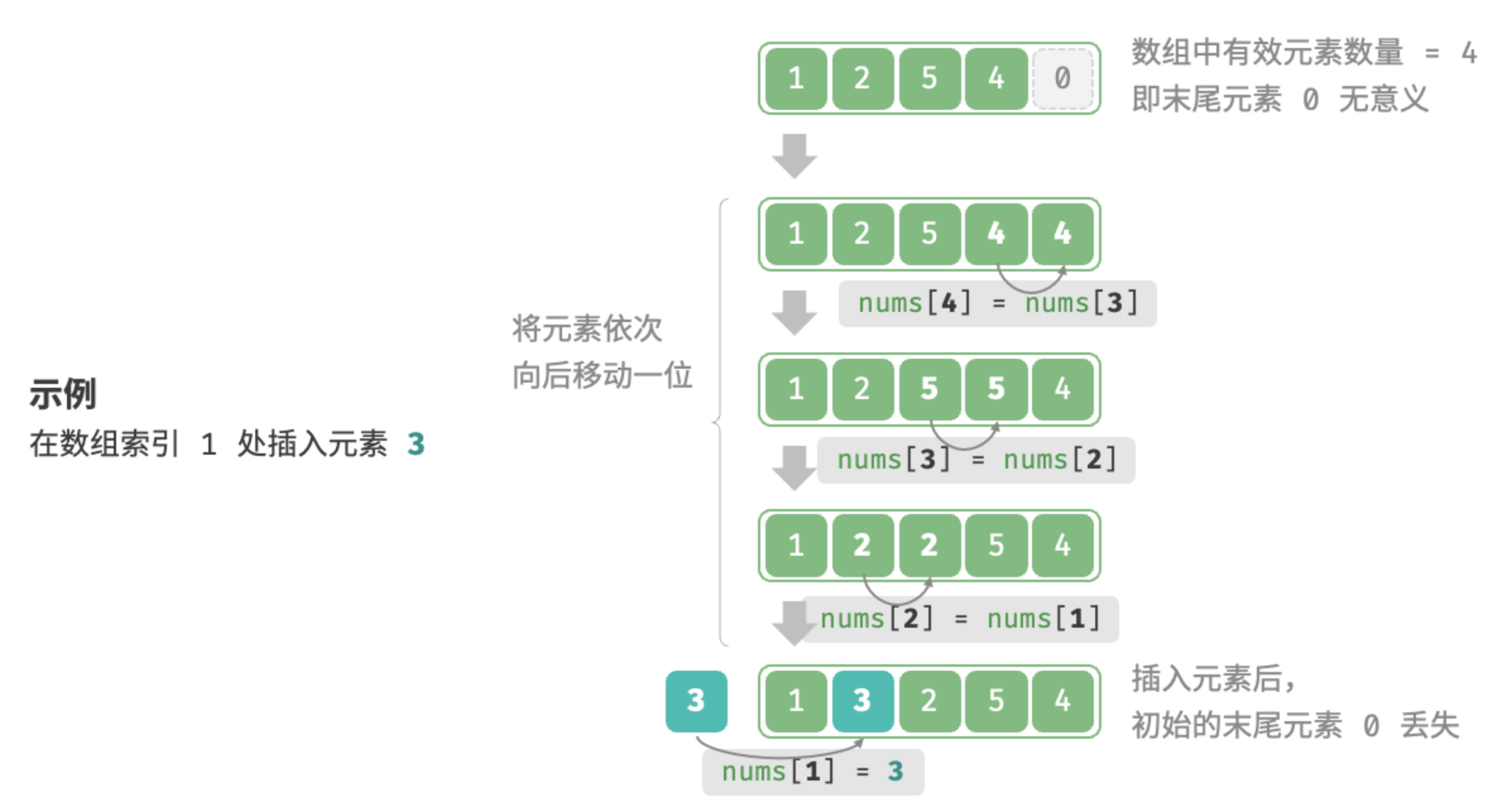
图示中的元素丢失概念:由于数组的长度是固定的,如果新插入一个元素则会导致尾部元素丢失
/* 在数组的索引 index 处插入元素 num */
void insert(int[] nums, int num, int index) {
// 把索引 index 以及之后的所有元素向后移动一位
for (int i = nums.length - 1; i > index; i--) {
nums[i] = nums[i - 1];
}
// 将 num 赋给 index 处的元素
nums[index] = num;
}
删除元素
同理,结合图示理解,如果想要删除索引 i 出的元素,则需要将索引 i 之后的元素都向前移动一位
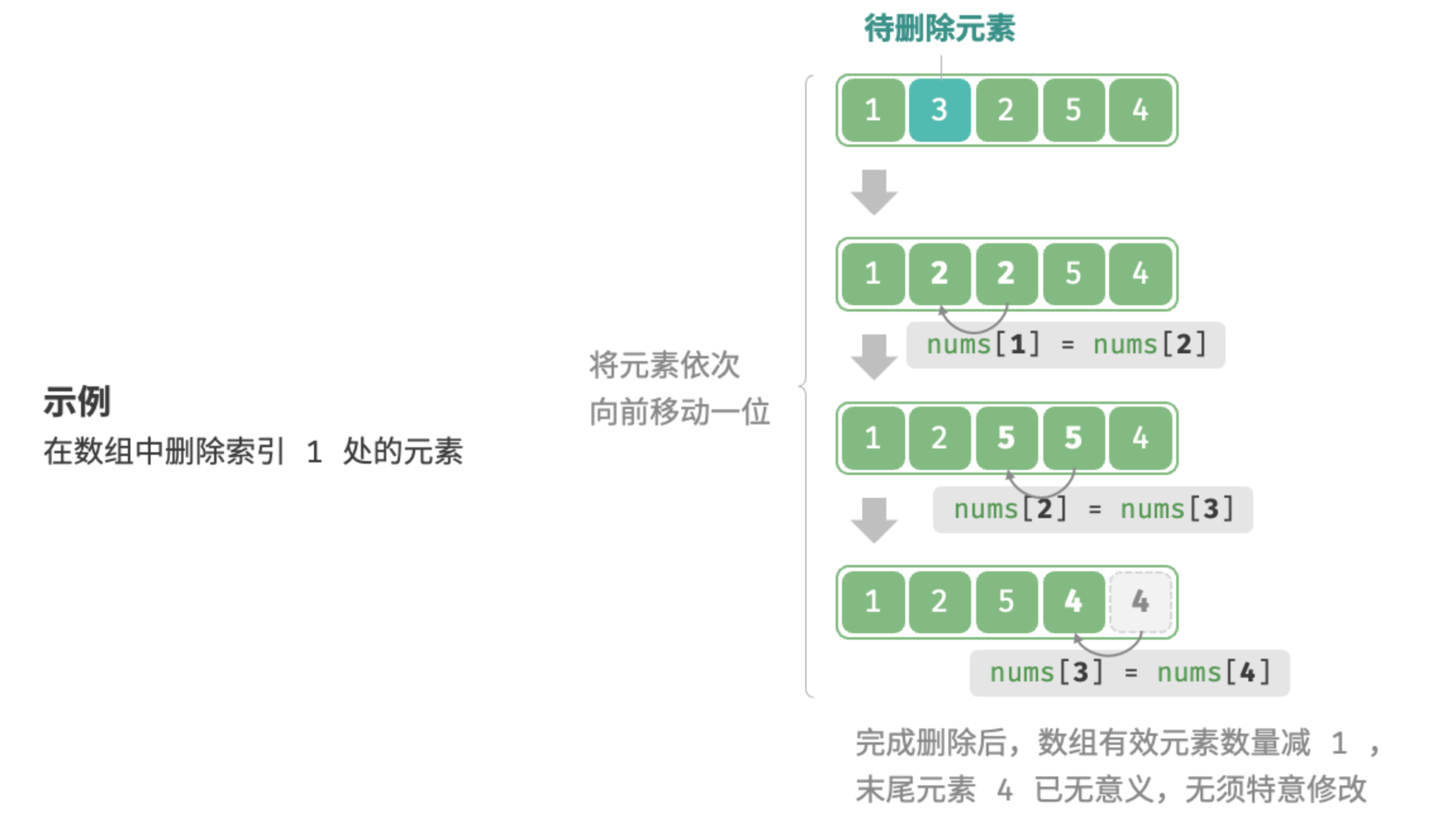
/* 删除索引 index 处的元素 */
void remove(int[] nums, int index) {
// 把索引 index 之后的所有元素向前移动一位
for (int i = index; i < nums.length - 1; i++) {
nums[i] = nums[i + 1];
}
}
综合分析来看,数组的插入与删除操作有以下缺点:
- 时间复杂度高:数组的插入和删除的平均时间复杂度均为 O(n) ,其中 n 为数组长度。
- 丢失元素:由于数组的长度不可变,因此在插入元素后,超出数组长度范围的元素会丢失。
- 内存浪费:可以初始化一个比较长的数组,只用前面一部分,这样在插入数据时,丢失的末尾元素都是“无意义”的,但这样做会造成部分内存空间浪费
遍历数组
在大多数编程语言中,既可以通过索引遍历数组,也可以直接遍历获取数组中的每个元素
/* 遍历数组 */
void traverse(int[] nums) {
int count = 0;
// 通过索引遍历数组
for (int i = 0; i < nums.length; i++) {
count += nums[i];
}
// 直接遍历数组元素
for (int num : nums) {
count += num;
}
}
查找元素
在数组中查找指定元素需要遍历数组,每轮判断元素值是否匹配,若匹配则输出对应索引。因为数组是线性数据结构,所以上述查找操作被称为“线性查找”
/* 在数组中查找指定元素 */
int find(int[] nums, int target) {
for (int i = 0; i < nums.length; i++) {
if (nums[i] == target)
return i;
}
return -1;
}
扩容数组
在复杂的系统环境中,程序难以保证数组之后的内存空间是可用的,从而无法安全地扩展数组容量。因此在大多数编程语言中,数组的长度是不可变的。
如果希望扩容数组,则需重新建立一个更大的数组,然后把原数组元素依次复制到新数组。这是一个 O(n) 的操作,在数组很大的情况下非常耗时。
/* 扩展数组长度 */
int[] extend(int[] nums, int enlarge) {
// 初始化一个扩展长度后的数组
int[] res = new int[nums.length + enlarge];
// 将原数组中的所有元素复制到新数组
for (int i = 0; i < nums.length; i++) {
res[i] = nums[i];
}
// 返回扩展后的新数组
return res;
}
2.数组的优点和局限性
数组存储在连续的内存空间内,且元素类型相同。这种做法包含丰富的先验信息,系统可以利用这些信息来优化数据结构的操作效率
- 空间效率高:数组为数据分配了连续的内存块,无须额外的结构开销
- 支持随机访问:数组允许在 O(1) 时间内访问任何元素
- 缓存局部性:当访问数组元素时,计算机不仅会加载它,还会缓存其周围的其他数据,从而借助高速缓存来提升后续操作的执行速度
连续空间存储是一把双刃剑,其存在以下局限性
- 插入与删除效率低:当数组中元素较多时,插入与删除操作需要移动大量的元素
- 长度不可变:数组在初始化后长度就固定了,扩容数组需要将所有数据复制到新数组,开销很大
- 空间浪费:如果数组分配的大小超过实际所需,那么多余的空间就被浪费了
3.数组典型应用
数组是一种基础且常见的数据结构,既频繁应用在各类算法之中,也可用于实现各种复杂数据结构
- 随机访问:如果想随机抽取一些样本,那么可以用数组存储,并生成一个随机序列,根据索引实现随机抽样
- 排序和搜索:数组是排序和搜索算法最常用的数据结构(快速排序、归并排序、二分查找等都主要在数组上进行)
- 查找表:当需要快速查找一个元素或其对应关系时,可以使用数组作为查找表。假如想实现字符到 ASCII 码的映射,则可以将字符的 ASCII 码值作为索引,对应的元素存放在数组中的对应位置
- 机器学习:神经网络中大量使用了向量、矩阵、张量之间的线性代数运算,这些数据都是以数组的形式构建的(数组是神经网络编程中最常使用的数据结构)
- 数据结构实现:数组可以用于实现栈、队列、哈希表、堆、图等数据结构(例如,图的邻接矩阵表示实际上是一个二维数组)
链表
1.链表常用操作
初始化链表
建立链表分为两步,第一步是初始化各个节点对象,第二步是构建节点之间的引用关系。初始化完成后就可以从链表的头节点出发,通过引用指向 next 依次访问所有节点
/* 初始化链表 1 -> 3 -> 2 -> 5 -> 4 */
// 1.初始化各个节点
ListNode n0 = new ListNode(1);
ListNode n1 = new ListNode(3);
ListNode n2 = new ListNode(2);
ListNode n3 = new ListNode(5);
ListNode n4 = new ListNode(4);
// 2.构建节点之间的引用
n0.next = n1;
n1.next = n2;
n2.next = n3;
n3.next = n4;
插入节点
在链表中插入节点非常容易。结合图示分析,如果想在相邻的两个节点 n0 和 n1 之间插入一个新节点 P ,则只需改变两个节点引用(指针)即可,时间复杂度为 O(1) 。相比之下,在数组中插入元素的时间复杂度为 O(n) ,在大数据量下的效率较低
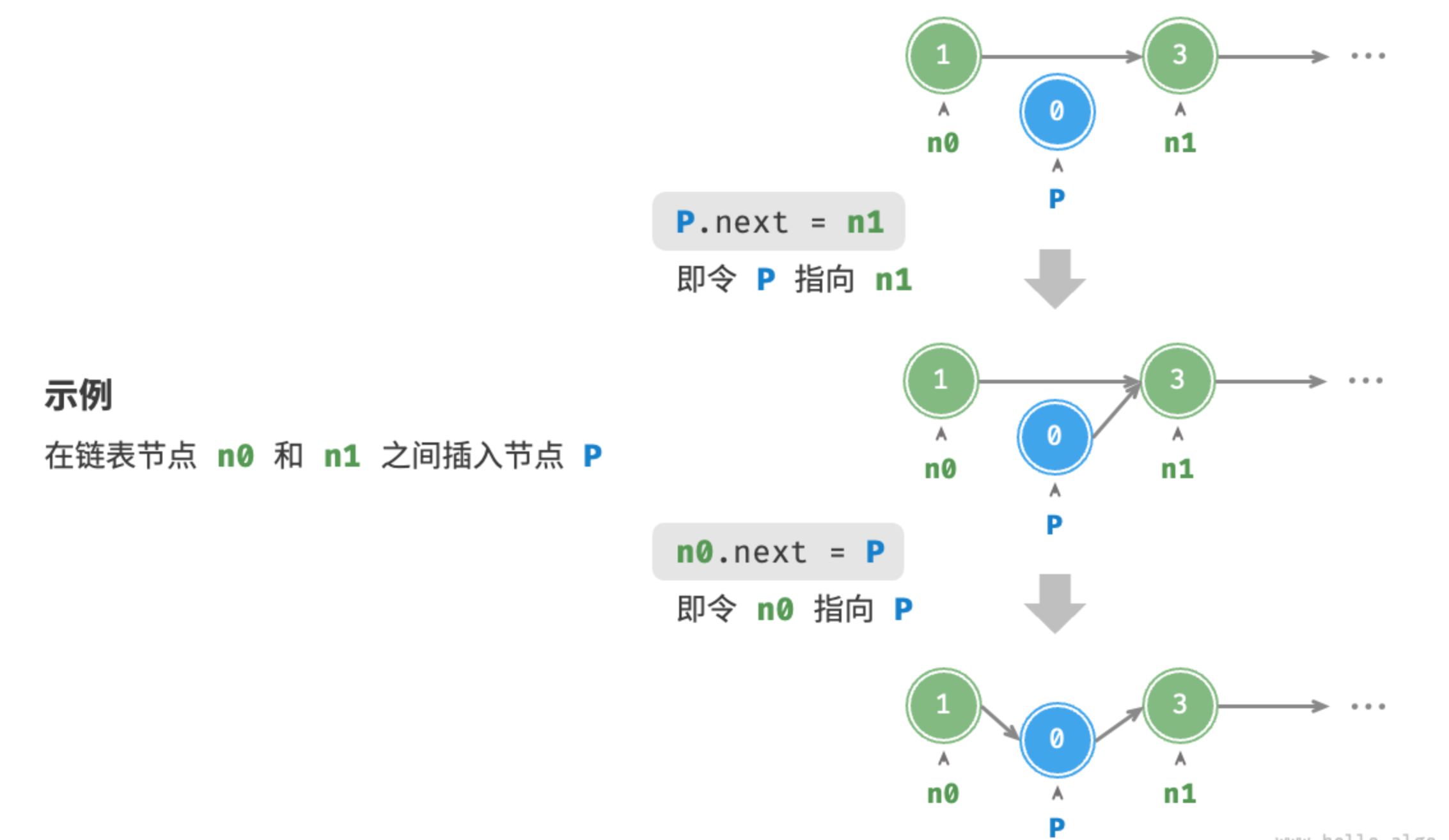
/* 在链表的节点 n0 之后插入节点 P */
void insert(ListNode n0, ListNode P) {
ListNode n1 = n0.next;
P.next = n1;
n0.next = P;
}
删除节点
在链表中删除节点也非常方便,只需改变一个节点的引用(指针)即可。需注意的是,尽管在删除操作完成后节点 P 仍然指向 n1 ,但实际上遍历此链表已经无法访问到 P ,这意味着 P 已经不再属于该链表了
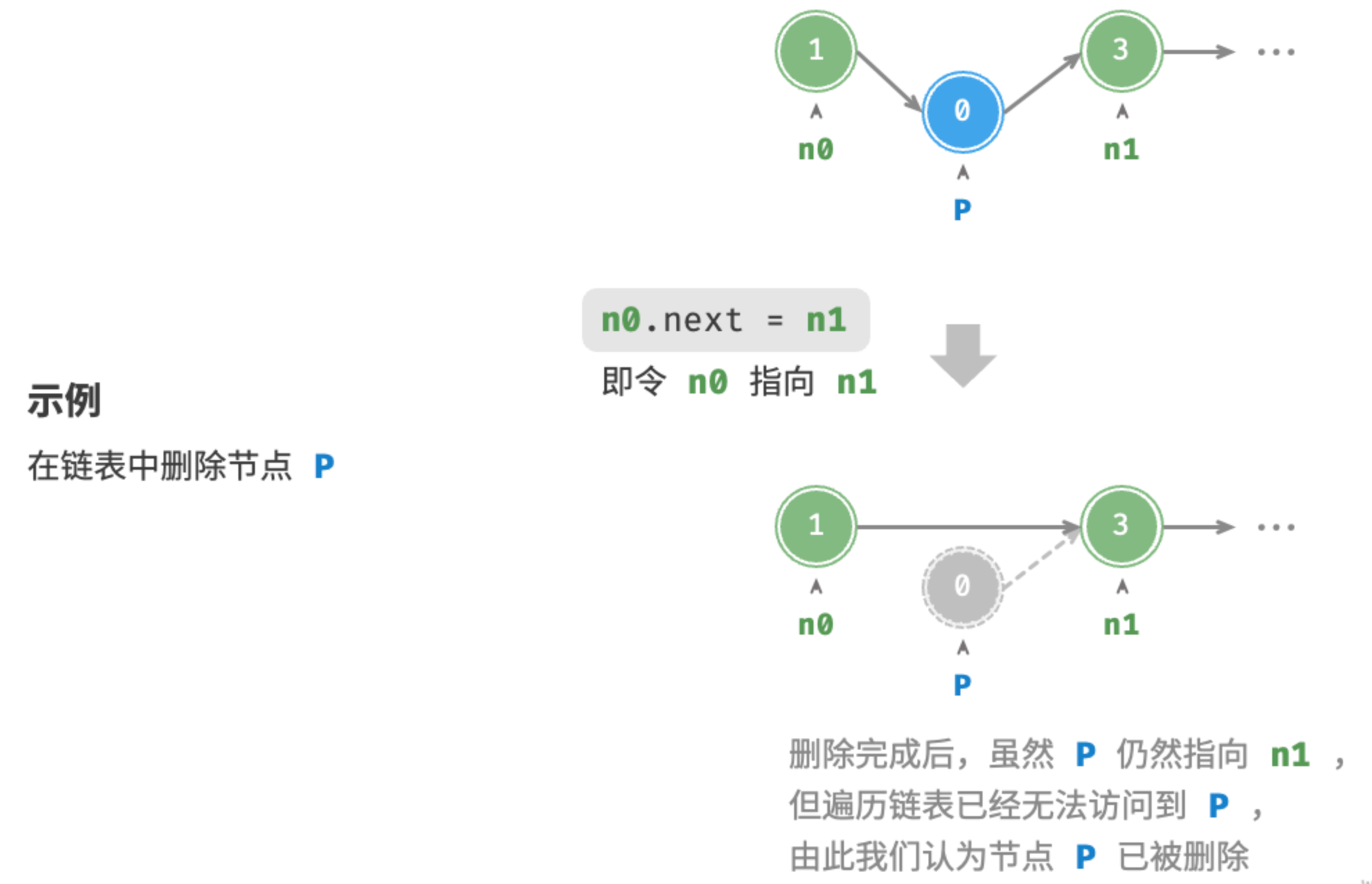
/* 删除链表的节点 n0 之后的首个节点 */
void remove(ListNode n0) {
if (n0.next == null)
return;
// n0 -> P -> n1
ListNode P = n0.next;
ListNode n1 = P.next;
n0.next = n1;
}
访问节点
在链表中访问节点的效率较低,需要从头节点出发,逐个向后遍历,直至找到目标节点。也就是说,访问链表的第 i 个节点需要循环 i−1 轮,时间复杂度为 O(n)
/* 访问链表中索引为 index 的节点 */
ListNode access(ListNode head, int index) {
for (int i = 0; i < index; i++) {
if (head == null)
return null;
head = head.next;
}
return head;
}
查找节点
遍历链表,查找指定值,输出该节点在链表中的索引,如果不存在则返回-1。这个过程也是属于线性查找
/* 在链表中查找值为 target 的首个节点 */
int find(ListNode head, int target) {
int index = 0;
while (head != null) {
if (head.val == target)
return index;
head = head.next;
index++;
}
return -1;
}
2.数组 VS 链表
| 效率对比 | 数组 | 链表 |
|---|---|---|
| 存储方式 | 连续内存空间 | 分散内存空间 |
| 容量扩展 | 长度不可变 | 可灵活扩展 |
| 内存效率 | 元素占用内存少、但可能浪费空间 | 元素占用内存多 |
| 访问元素 | O(1) | O(n) |
| 添加元素 | O(n) | O(1) |
| 删除元素 | O(n) | O(1) |
3.常见链表类型
- 单向链表:即普通链表。单向链表的节点包含值和指向下一节点的引用两项数据。将首个节点称为头节点,将最后一个节点称为尾节点,尾节点指向空
None - 环形链表:如果令单向链表的尾节点指向头节点(首尾相接),则得到一个环形链表。在环形链表中,任意节点都可以视作头节点
- 双向链表:与单向链表相比,双向链表记录了两个方向的引用。双向链表的节点定义同时包含指向后继节点(下一个节点)和前驱节点(上一个节点)的引用(指针)。相较于单向链表,双向链表更具灵活性,可以朝两个方向遍历链表,但相应地也需要占用更多的内存空间
/* 双向链表节点类 */
class ListNode {
int val; // 节点值
ListNode next; // 指向后继节点的引用
ListNode prev; // 指向前驱节点的引用
ListNode(int x) { val = x; } // 构造函数
}
.assets/image-20240814165215974.png)
4.链表典型应用
单向链表通常用于实现栈、队列、哈希表和图等数据结构
栈与队列:
- 栈:当插入和删除操作都在链表的一端进行时,它表现的特性为先进后出,对应栈;
- 队列:当插入操作在链表的一端进行,删除操作在链表的另一端进行,它表现的特性为先进先出,对应队列;
哈希表:链式地址是解决哈希冲突的主流方案之一,在该方案中,所有冲突的元素都会被放到一个链表中
图:邻接表是表示图的一种常用方式,其中图的每个顶点都与一个链表相关联,链表中的每个元素都代表与该顶点相连的其他顶点
双向链表常用于需要快速查找前一个和后一个元素的场景
高级数据结构:比如在红黑树、B 树中,需要访问节点的父节点,这可以通过在节点中保存一个指向父节点的引用来实现,类似于双向链表。
浏览器历史:在网页浏览器中,当用户点击前进或后退按钮时,浏览器需要知道用户访问过的前一个和后一个网页,双向链表的特性使得这种操作变得简单。
LRU 算法:在缓存淘汰(LRU)算法中,需要快速找到最近最少使用的数据,以及支持快速添加和删除节点
环形链表常用于需要周期性操作的场景,比如操作系统的资源调度
时间片轮转调度算法:在操作系统中,时间片轮转调度算法是一种常见的 CPU 调度算法,它需要对一组进程进行循环。每个进程被赋予一个时间片,当时间片用完时,CPU 将切换到下一个进程。这种循环操作可以通过环形链表来实现。
数据缓冲区:在某些数据缓冲区的实现中,也可能会使用环形链表。比如在音频、视频播放器中,数据流可能会被分成多个缓冲块并放入一个环形链表,以便实现无缝播放
列表
列表(list)是一个抽象的数据结构概念,它表示元素的有序集合,支持元素访问、修改、添加、删除和遍历等操作,无须使用者考虑容量限制的问题。列表可以基于链表或数组实现。
- 链表天然可以看作一个列表,其支持元素增删查改操作,并且可以灵活动态扩容
- 数组也支持元素增删查改,但由于其长度不可变,因此只能看作一个具有长度限制的列表
当使用数组实现列表时,长度不可变的性质会导致列表的实用性降低。这是因为通常无法事先确定需要存储多少数据,从而难以选择合适的列表长度。若长度过小,则很可能无法满足使用需求;若长度过大,则会造成内存空间浪费
为解决此问题,可以使用动态数组(dynamic array)来实现列表。它继承了数组的各项优点,并且可以在程序运行过程中进行动态扩容
实际上,许多编程语言中的标准库提供的列表是基于动态数组实现的,例如 Python 中的 list 、Java 中的 ArrayList 、C++ 中的 vector 和 C# 中的 List 等。在接下来的讨论中,将把“列表”和“动态数组”视为等同的概念
1.列表常用操作
初始化列表
通常使用“无初始值”和“有初始值”这两种初始化方法
/* 初始化列表 */
// 无初始值
List<Integer> nums1 = new ArrayList<>();
// 有初始值(注意数组的元素类型需为 int[] 的包装类 Integer[])
Integer[] numbers = new Integer[] { 1, 3, 2, 5, 4 };
List<Integer> nums = new ArrayList<>(Arrays.asList(numbers));
访问元素
列表本质上是数组,因此可以在 O(1) 时间内访问和更新元素,效率很高
/* 访问元素 */
int num = nums.get(1); // 访问索引 1 处的元素
/* 更新元素 */
nums.set(1, 0); // 将索引 1 处的元素更新为 0
插入与删除元素
相较于数组,列表可以自由地添加与删除元素。在列表尾部添加元素的时间复杂度为 O(1) ,但插入和删除元素的效率仍与数组相同,时间复杂度为 O(n)
/* 清空列表 */
nums.clear();
/* 在尾部添加元素 */
nums.add(1);
nums.add(3);
nums.add(2);
nums.add(5);
nums.add(4);
/* 在中间插入元素 */
nums.add(3, 6); // 在索引 3 处插入数字 6
/* 删除元素 */
nums.remove(3); // 删除索引 3 处的元素
遍历列表
/* 通过索引遍历列表 */
int count = 0;
for (int i = 0; i < nums.size(); i++) {
count += nums.get(i);
}
/* 直接遍历列表元素 */
for (int num : nums) {
count += num;
}
拼接列表
给定一个新列表 nums1 ,可以将其拼接到原列表的尾部。
/* 拼接两个列表 */
List<Integer> nums1 = new ArrayList<>(Arrays.asList(new Integer[] { 6, 8, 7, 10, 9 }));
nums.addAll(nums1); // 将列表 nums1 拼接到 nums 之后
排序列表
完成列表排序后,便可以使用在数组类算法题中经常考查的“二分查找”和“双指针”算法
/* 排序列表 */
Collections.sort(nums); // 排序后,列表元素从小到大排列
2.列表实现
许多编程语言内置了列表,例如 Java、C++、Python 等。它们的实现比较复杂,各个参数的设定也非常考究,例如初始容量、扩容倍数等。感兴趣的读者可以查阅源码进行学习。
可以结合上述列表的操作分析列表的实现,加深对列表工作原理的理解,尝试实现一个简易版列表,包括以下三个重点设计。
- 初始容量:选取一个合理的数组初始容量。示例中选择 10 作为初始容量
- 数量记录:声明一个变量
size,用于记录列表当前元素数量,并随着元素插入和删除实时更新。根据此变量,可以定位列表尾部,以及判断是否需要扩容 - 扩容机制:若插入元素时列表容量已满,则需要进行扩容。先根据扩容倍数创建一个更大的数组,再将当前数组的所有元素依次移动至新数组。示例中规定每次将数组扩容至之前的 2 倍
/* 列表类 */
class MyList {
private int[] arr; // 数组(存储列表元素)
private int capacity = 10; // 列表容量
private int size = 0; // 列表长度(当前元素数量)
private int extendRatio = 2; // 每次列表扩容的倍数
/* 构造方法 */
public MyList() {
arr = new int[capacity];
}
/* 获取列表长度(当前元素数量) */
public int size() {
return size;
}
/* 获取列表容量 */
public int capacity() {
return capacity;
}
/* 访问元素 */
public int get(int index) {
// 索引如果越界,则抛出异常,下同
if (index < 0 || index >= size)
throw new IndexOutOfBoundsException("索引越界");
return arr[index];
}
/* 更新元素 */
public void set(int index, int num) {
if (index < 0 || index >= size)
throw new IndexOutOfBoundsException("索引越界");
arr[index] = num;
}
/* 在尾部添加元素 */
public void add(int num) {
// 元素数量超出容量时,触发扩容机制
if (size == capacity())
extendCapacity();
arr[size] = num;
// 更新元素数量
size++;
}
/* 在中间插入元素 */
public void insert(int index, int num) {
if (index < 0 || index >= size)
throw new IndexOutOfBoundsException("索引越界");
// 元素数量超出容量时,触发扩容机制
if (size == capacity())
extendCapacity();
// 将索引 index 以及之后的元素都向后移动一位
for (int j = size - 1; j >= index; j--) {
arr[j + 1] = arr[j];
}
arr[index] = num;
// 更新元素数量
size++;
}
/* 删除元素 */
public int remove(int index) {
if (index < 0 || index >= size)
throw new IndexOutOfBoundsException("索引越界");
int num = arr[index];
// 将将索引 index 之后的元素都向前移动一位
for (int j = index; j < size - 1; j++) {
arr[j] = arr[j + 1];
}
// 更新元素数量
size--;
// 返回被删除的元素
return num;
}
/* 列表扩容 */
public void extendCapacity() {
// 新建一个长度为原数组 extendRatio 倍的新数组,并将原数组复制到新数组
arr = Arrays.copyOf(arr, capacity() * extendRatio);
// 更新列表容量
capacity = arr.length;
}
/* 将列表转换为数组 */
public int[] toArray() {
int size = size();
// 仅转换有效长度范围内的列表元素
int[] arr = new int[size];
for (int i = 0; i < size; i++) {
arr[i] = get(i);
}
return arr;
}
}
内存与缓存
在前面的学习中探讨了数组和链表这两种基础且重要的数据结构,它们分别代表了“连续存储”和“分散存储”两种物理结构。实际上,物理结构在很大程度上决定了程序对内存和缓存的使用效率,进而影响算法程序的整体性能
1.计算机存储设备
计算机中包括三种类型的存储设备:硬盘(hard disk)、内存(random-access memory, RAM)、缓存(cache memory)。下表展示了它们在计算机系统中的不同角色和性能特点
| 计算机的存储设备 | 硬盘 | 内存 | 缓存 |
|---|---|---|---|
| 用途 | 长期存储数据,包括操作系统、程序、文件等 | 临时存储当前运行的程序和正在处理的数据 | 存储经常访问的数据和指令,减少 CPU 访问内存的次数 |
| 易失性 | 断电后数据不会丢失 | 断电后数据会丢失 | 断电后数据会丢失 |
| 容量 | 较大,TB 级别 | 较小,GB 级别 | 非常小,MB 级别 |
| 速度 | 较慢,几百到几千 MB/s | 较快,几十 GB/s | 非常快,几十到几百 GB/s |
| 价格 | 较便宜,几毛到几元 / GB | 较贵,几十到几百元 / GB | 非常贵,随 CPU 打包计价 |
可以将计算机存储系统想象为图示的金字塔结构。越靠近金字塔顶端的存储设备的速度越快、容量越小、成本越高。这种多层级的设计并非偶然,而是计算机科学家和工程师们经过深思熟虑的结果。
- 硬盘难以被内存取代。首先,内存中的数据在断电后会丢失,因此它不适合长期存储数据;其次,内存的成本是硬盘的几十倍,这使得它难以在消费者市场普及。
- 缓存的大容量和高速度难以兼得。随着 L1、L2、L3 缓存的容量逐步增大,其物理尺寸会变大,与 CPU 核心之间的物理距离会变远,从而导致数据传输时间增加,元素访问延迟变高。在当前技术下,多层级的缓存结构是容量、速度和成本之间的最佳平衡点。
总的来说,硬盘用于长期存储大量数据,内存用于临时存储程序运行中正在处理的数据,而缓存则用于存储经常访问的数据和指令,以提高程序运行效率。三者共同协作,确保计算机系统高效运行。
在程序运行时,数据会从硬盘中被读取到内存中,供 CPU 计算使用。缓存可以看作 CPU 的一部分,它通过智能地从内存加载数据,给 CPU 提供高速的数据读取,从而显著提升程序的执行效率,减少对较慢的内存的依赖
.assets/image-20240814170933158.png)
2.数据结构的内存效率
在内存空间利用方面,数组和链表各自具有优势和局限性。
一方面,内存是有限的,且同一块内存不能被多个程序共享,因此希望数据结构能够尽可能高效地利用空间。数组的元素紧密排列,不需要额外的空间来存储链表节点间的引用(指针),因此空间效率更高。然而,数组需要一次性分配足够的连续内存空间,这可能导致内存浪费,数组扩容也需要额外的时间和空间成本。相比之下,链表以“节点”为单位进行动态内存分配和回收,提供了更大的灵活性。
另一方面,在程序运行时,随着反复申请与释放内存,空闲内存的碎片化程度会越来越高,从而导致内存的利用效率降低。数组由于其连续的存储方式,相对不容易导致内存碎片化。相反,链表的元素是分散存储的,在频繁的插入与删除操作中,更容易导致内存碎片化
3.数据结构的缓存效率
缓存虽然在空间容量上远小于内存,但它比内存快得多,在程序执行速度上起着至关重要的作用。由于缓存的容量有限,只能存储一小部分频繁访问的数据,因此当 CPU 尝试访问的数据不在缓存中时,就会发生缓存未命中(cache miss),此时 CPU 不得不从速度较慢的内存中加载所需数据。
显然,“缓存未命中”越少,CPU 读写数据的效率就越高,程序性能也就越好。将 CPU 从缓存中成功获取数据的比例称为缓存命中率(cache hit rate),这个指标通常用来衡量缓存效率。
为了尽可能达到更高的效率,缓存会采取以下数据加载机制
- 缓存行:缓存不是单个字节地存储与加载数据,而是以缓存行为单位。相比于单个字节的传输,缓存行的传输形式更加高效
- 预取机制:处理器会尝试预测数据访问模式(例如顺序访问、固定步长跳跃访问等),并根据特定模式将数据加载至缓存之中,从而提升命中率
- 空间局部性:如果一个数据被访问,那么它附近的数据可能近期也会被访问。因此,缓存在加载某一数据时,也会加载其附近的数据,以提高命中率
- 时间局部性:如果一个数据被访问,那么它在不久的将来很可能再次被访问。缓存利用这一原理,通过保留最近访问过的数据来提高命中率
实际上,数组和链表对缓存的利用效率是不同的,主要体现在以下几个方面
- 占用空间:链表元素比数组元素占用空间更多,导致缓存中容纳的有效数据量更少
- 缓存行:链表数据分散在内存各处,而缓存是“按行加载”的,因此加载到无效数据的比例更高
- 预取机制:数组比链表的数据访问模式更具“可预测性”,即系统更容易猜出即将被加载的数据
- 空间局部性:数组被存储在集中的内存空间中,因此被加载数据附近的数据更有可能即将被访问
总体而言,数组具有更高的缓存命中率,因此它在操作效率上通常优于链表。这使得在解决算法问题时,基于数组实现的数据结构往往更受欢迎
需要注意的是,高缓存效率并不意味着数组在所有情况下都优于链表。实际应用中选择哪种数据结构,应根据具体需求来决定。例如,数组和链表都可以实现“栈”数据结构,但它们适用于不同场景。
- 在做算法题时,一般会倾向于选择基于数组实现的栈,因为它提供了更高的操作效率和随机访问的能力,代价仅是需要预先为数组分配一定的内存空间。
- 如果数据量非常大、动态性很高、栈的预期大小难以估计,那么基于链表实现的栈更加合适。链表能够将大量数据分散存储于内存的不同部分,并且避免了数组扩容产生的额外开销
